Methods for Determining the Solubility Parameter of Additives for Lubricating Oils

Introduction

In order to be used to improve the viscosity index, mineral oils must be good solvents for the polymers to be used. If the oil is a good solvent for the polymer, the polymer-solvent interactions cause the solvent to penetrate into the macromolecular scales, which are of considerable size and the solution has a high viscosity.

In order to appreciate how good solvent is SAE 10W oil – whose solubility parameter is not known – for the KELTAN 4200 copolymer, it was determined on the one hand its intrinsic viscosity in oil and on other global and partial solubility parameters.

Determination of the overall and partial solubility parameters of the copolymer was performed by the intrinsic viscosity method. The intrinsic viscosity can be used to determine the solubility parameters because this is a measure of the size of the macromolecule bundles of the polymer in a given solvent. The intrinsic viscosity has specific volume dimensions, and can be considered as the sum of the effective hydrodynamic volumes of the molecules constituting 1 g of the polymer.¹ When the solution is infinitely diluted, the molecules do not interact with each other and this volume is the sum of the effective hydrodynamic volumes of the separate molecules. Thus, the intrinsic viscosity of a polymer in a given solvent is directly related to its molar mass, being a measure of the volume occupied by the individual molecules. In the case of the same polymer in different solvents, it reflects the interaction between the polymer and solvent segments at infinite dilution and is a measure of the dissolution rate of the solvent for the considered polymer.²

Intrinsic viscosities can be determined from one-strength viscosity measurements using empirical Huggins relations⁴:

and/or Kraemer³:

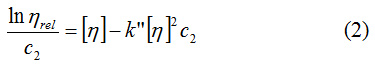
where k‘ is the constant Huggins, or k” – the constant Kraemer.

Constanta k ‘is dependent on the polymer-solvent system and temperature and only describes the interactions resulting from differences in chemical structure of the polymer and/or solvent. Reduced interaction between dissolved macromolecules, expressed by small values of the constant, ranging from 0.3 to 0.4, reflects high dissolution power for the given polymer.

Constanta k “depends on the same factors but has lower values ranging from 0.1 to 0.2. The Huggins constant is often preferred because the  slope is smaller and the order of origin is more definite.⁵

By combining the two equations, the theoretical value of the algebraic sum of the two constants must be 0.5.

To obtain correct values for intrinsic viscosity with relation (1), the k ‘values must be between 0.3 and 0.4.⁶

To determine the solubility parameter, it is necessary to know the intrinsic viscosities of the polymer in as many solvents with different solubility parameters, so it is necessary to perform the dissolution tests in the solvents selected according to the solubility parameters, taking into account that KELTAN 4200 is a non-polar copolymer and that SAE 10W oil is predominantly paraffinic.

Solvents used, global solubility parameters, δ, and partial, δ_d, δp and δ_h, [7] in order of increase of the global solubility parameter values, as well as the results of the dissolution tests, are presented in Table 1.⁸

Table 1: Solvents used, partial solubility parameters and and the solubility of the copolymer.⁸

Solvents	δ(MPa)1/2	δd(MPa)1/2	δp(MPa)1/2	δh(MPa)1/2	Observaţii
n-Heptane	15.3	15.3	0	0	Soluble
Cyclohexane	16.8	16.8	0	0.2	Soluble
Benzene	18.6	18.4	0	2	Soluble
Toluene	18.2	18	1.4	2	Soluble
o-xylene	18	17.8	1	3.1	Soluble
Methyl-ethyl cetone	19	16	9	5.1	Do not get soaked
Cyclohexanone (20°C)	19.6	17.8	6.3	5.1	A little soaked
Ehyl acetate (20°C)	18.2	15.8	5.3	7.2	It is soaked very little
Ethane dichloride	18.4	16.6	8.2	0.4	Very poorly soaked
Chloroform	19	17.8	3.1	5.7	Soluble
Carbon tetrachloride	17.8	17.8	0	0.6	Soluble
Trichlorethylene (20°C)	19	18	3.1	5.3	Soluble
Benzene chloride	19.6	19	4.3	2	Soluble

 

In this paper I have been looking at the determination of the solubility parameter for the polyethylene-propylene copolymer by two methods.

Materials and Method

The following copolymer were used as: poly(ethylene-co-propylene) (DSM Elastomers Europe B.V.), trade name KELTAN 4200. As mineral oil SAE 10W (INCERP, Romania) was used. The mineral oil SAE 10W has the following characteristics: density – 0.8727 g/cm³, viscosity at 100°C – 5 cSt (ASTM D 4648 method) and viscosity index 90.

The viscosities of the dilute solutions were determined using Oa and I viscosimeters of the Ubbelodhe Schott capillary-type Viscosimeter set with the 0.04887 and 0.00976 constants at 25°C±0,1°C. [8] Viscosimeters were selected in such a way that the allowed measurement error limits and Hagenbach-Couette correction^11-13 for kinetic energy could not be exceeded in order to increase the accuracy of the determinations.

Dissolution was carried out at room temperature, allowing the copolymer to soak for a long period of time and then gently shaking manually to avoid its degradation by agitation.

Results and discussion

Table 2 shows the intrinsic viscosity values for 14 solvents in which KELTAN 4200 copolymer is dissolved. Table 2 shows that the intrinsic viscosity value of the copolymer in SAE 10 W oil is very close to that in n-heptane, which can be explained by the fact that the oil is predominantly paraffinic. By computing the Huggins constants for n-heptane and oil, the values are greater than 0.4 but very close to each other: 0.58 for n-heptane and 0.67 for oil. It can be appreciated, however, that SAE 10 W oil is a fairly good solvent for the ethylene-propylene copolymer.

Table 2. The solvents used, the intrinsic viscosities of the copolymer in the specified solvents and the intrinsic viscosities normed at the unit⁸

Nr. crt.	Solvent	[η], dL/g	[η]’
1.	n-Heptane	1.5738	0.6062
2.	Cyclohexane	2.2385	0.8622
3.	Benzene	0.6871	0.2646
4.	Toluene	0.7289	0.2807
5.	o-Xylene	1.2697	0.4890
6.	Methyl-ethyl cetone	–	–
7.	Cyclohexanone	–	–
8.	Ehyl acetate	–	–
9.	Ethane dichloride	–	–
10.	Chloroform	0.4726	0.1820
11.	Carbon tetrachloride	2.5962*	1.0000
12.	Trichlorethylene	1.6174	0.6229
13.	Benzene chloride	0.6370	0.2453
14.	oil SAE 10W	1.5355	0.5914

 

* the maximum intrinsic viscosity value

Considering the intrinsic viscosity values, the best solvent is carbon tetrachloride, followed by cyclohexane, trichloethylene and heptane, and the weakest chloroform with the highest solubility parameter due to hydrogen bonding between solvents. This is explained by the composition of the copolymer, which has a nonpolar structure.

If the Huggins constants are to be calculated, it is found that the values are less than 0.4 for the first two solvents alone, so obtaining intrinsic viscosities from the values determined for viscosities at a single concentration would have been correct only for these solvents.

Table 2 shows that the intrinsic viscosity value of the copolymer in SAE 10 W oil is very close to that in n-heptane, which can be explained by the fact that the oil is predominantly paraffinic. By computing the Huggins constants for n-heptane and oil, the values are greater than 0.4 but very close to each other: 0.58 for n-heptane and 0.67 for oil. It can be appreciated, however, that SAE 10 W oil is a fairly good solvent for the ethylene-propylene copolymer.

Determination of the partial and global solubility parameters was made in the first step using the Hansen method.

Figure 1 shows the pairs of solubility parameters δ_p-2δd, δ_h-2δ_d and δ_h-δ_p of the solvents and unsolvates of the polymer listed in Table 1 in rectangular axle systems, number 2 in front of the solubility parameter due to dispersion forces indicating the twice the magnitude taken on this axis. The circle with the first pair (Figure 1a) was then drawn so that as many solvents could be contained within it. The coordinates of the center of the circle represent the values of the partial solubility parameters corresponding to the polymer – δ_pp şi δ_pd – the first index indicating the polymer, and its radius – its interaction. Then the representation for the pair was performed δ_h – 2δ_d (figure 1b) keeping value for both δ_pd as well as for the range of interaction, and the value was established δ_ph. The correctness of the results was then checked by drawing the circle for the pair δ_h – δ_p with the already determined values and range of interaction (figure 1c).

The global solubility parameter was calculated with relation (3), and the sphere of interaction sphere with (4).

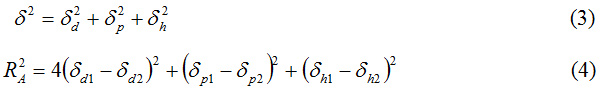
Figure 1: Plane representation of pairs of solubility parameters: Click here to view figure

 

a – δ_p-2δ_d, b – δ_h-2δ_d and c – δ_h-δ_p for: 1 – benzene, 2 – toluene, 3 – o-xylene,

4 – ethyl acetate, 5 – chloroform, 6 – methyl ethyl ketone, 7 – n-heptane,

8 – 1,1-dichloroethane, 9 – cyclohexanone, 10 – trichlorethylene,

11 – carbon tetrachloride, 12 – chlorobenzene, 13 – cyclohexane

When plotting solubility parameter pairs for circle tracing, any of the pairs can be taken first, resulting in different values for the partial solubility parameters and for the sphere of solubility sphere. The values obtained for the solubility parameters and for the range of the copolymer interaction sphere:  δ_d = 17.5;  δ_p = 0.8;  δ_h = 1.0;  δ = 17.6 (MPa)^1/2,  respectively  R = 4.8 (MPa)^1/2 considered for the first representation the pair of partial solubility parameters δ_p-δ_d, which led to fixing the needles.

Given this dependence on the solubility parameter values,⁹ and another improved method for determining the Hansen solubility parameters were used to determine the above amounts.¹⁰ This determines faster and more accurately, based on a computation program, the Hansen solubility parameters and the sphere of the interaction sphere for the polymer based on already existing literature data relating to Hansen’s solvents parameters, by using the intrinsic viscosity of the polymer in the solvent given as a percentage of the solvent’s ability to dissolve the polymer.

Thus, each solvent is represented by a circle with a larger or smaller radius, depending on its solvent quality (the intrinsic viscosity value), and not by a point in diagrams such as those in Figure 1.

The equations of the coordinates of the mass center for the polymer, denoted by the p index, are¹⁰:

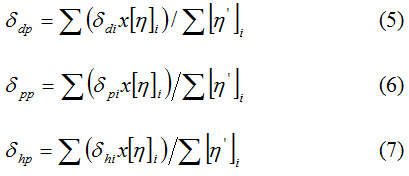
where i designates the solvent, or [η’]_i represents the intrinsic viscosity of the polymer in the solvent i normalized to the unit.

After determining the coordinates of the center of solubility sphere with the relations presented, the R_i distances from the center of the solubility sphere are calculated at the points corresponding to the good solvents and the weak solvents in the three-dimensional space. The highest R_i value found is considered to be the radius of the solubility sphere. The calculation relation for the distances R_i is equation (4).

For comparison, Table 3 presents the values ​​of the total partial solubility parameters, and the range of the sphere of interaction that were obtained by both methods.

By analyzing the values ​​determined by the two methods, it is found that the global solubility parameters have virtually equal values, while for the partial or differences obtained, between 0.1 (MPa)^1/2 for the one due to dispersion forces and 0.8 (MPa) ^1/2 for that due to polar interactions. Differences can be attributed to the intake of intrinsic viscosities for the improved method as well as to the determination method itself.

Table 3. Hansen parameters and the sphere of interaction sphere calculated by Hansen and improved [8]

Method	δdp (MPa)1/2	δpp (MPa)1/2	δhp (MPa)1/2	δ (MPa)1/2	R (MPa)1/2
Hansen	17.5	0.8	1.0	17.6	4.8
Improved	17.4	1.0	1.8	17.5	4.5

 

Values obtained for the interaction range are close, the Hansen method being 0.3 (MPa) ^1/2 higher, which may result in the inclusion of more unsolvates within the solubility volume of the solvent.

The values obtained for the overall solubility parameter are very close to that of the solvent in which the polymer has the highest intrinsic viscosity, i.e., carbon tetrachloride, as expected, considering that the solubility parameter of the polymer is considered equal to the solvent in which intrinsic viscosity is maximal.

Conclusion

The overall and partial solubility parameters due to dispersion forces have small values specific to non-polar polymers, and the partial ones due to polar interactions and hydrogen bonds have very low values ranging from 0.8 to 1.0 (MPa) ^1/2 if the Hansen method is used and between 1.0 and 1.8 (MPa) ^1/2 using the improved method, consistent with the copolymer structure.

References

1. Cilurzo F., Selmin F., Minghetti P., Montanari L., Lenardi C., Orsini F., Poletti G.; AAPS Pharm Sci Tech 2005, 6 ,  E586.
2. Qian J. W.,  Qi G. R., Ding X. Z., Yang S. L.; Fuel 1996, 75, 307.
3. Kraemer E. O.; Ind. Eng. Chem. 1938, 30, 1200.
4. Huggins M. L.; J. Amer. Chem. Soc. 1942, 64, 1712.
5. Mark D., Alger S. M.; “Polymer Science Dictionary”, Chapman & Hall, London, 1997.
6. Pilati F., Tosseli M.; Proceedings of the 15th Symposium of the Associazione Italiana di Scienza e Tecnologia delle Macromolecole, May 1993, Gargnano, Italy, lucr. 127.
7. Brandrup J., Immergut E.H.; “Polymer Handbook”, ed. 3-a, Wiley, New York, 1989.
8. Stanciu I., Leca M.; Materiale Plastice 2005, 42, 268-271.
9. Stanciu I., Leca M.; Bull. Petroleum-Gas Univ. Ploiesti, Technical Series 2007, LIX, 69-72.
10. Segărceanu O., Leca M.; Progr. Org. Coat. 1997, 31, 307.
11. Sperling L. H.; “Introduction to Physical Polymer Science“ ed. 4-a, Wiley, New York, 2006.
12. Stanciu I.; Journal of Science and Arts 2017, 4(41), 771-778.
13. Stanciu I.; Journal of Science and Arts 2018,  1(42), 197-202.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.