Microwave Dielectric Measurements of 4-Nitroacetanilide at Different Temperatures in Carbon Tetrachloride Solution

Introduction

4-Nitroacetanilide (IUPAC name N-(4-nitrophenyl)acetamide) is a chemical compound in the form of solid and in crystalline powder in yellow to green-yellow or yellow to green-brown color. Its chemical formula is C₈H₈N₂O₃ andmolecular weight is 180.163 (g/mol). It is used as a raw material to prepare some products.¹ Sometimes it is also used to make dyes.² It should be used very carefully because it could cause skin irritation, respiratory irritation and eye irritation etc. Its chemical structure is given as:

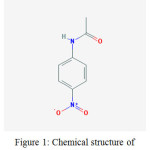Figure 1: Chemical structure of 4-Nitroacetanilide. Click here to View figure

 

Dielectric investigations of solutions are useful in finding construction and development of complexes in them because they are having different variety of connecting molecules. The dielectric relaxation studies in microwave region have been done by many researchers for polar molecules and their binary mixtures in the dilute solution of non polar solvents.^3-9 The dielectric investigations on binary mixtures of ethanol and N, N-dimethylformamide (DMF) with benzene at various temperatures and at a fixed frequency is done by Sharma et. all,¹⁰ with the help of standing microwave techniques. They found the existence of solute-solvent association between the molecules due to the polar nature of both solute and solvent. They also confirm that both the dielectric relaxation process and viscous flow process behaves as a rate process. In the present study we have performed some experiments to investigate dielectric properties and relaxation process of 4-Nitroacetanilide in the dilute solution of carbon tetrachloride. Such relaxation studies deliver useful outcomes regarding the self association, solute-solute type and solute-solvent type of association between polar molecules in microwave region. They are also important to recognize the Hydrogen bonding and inter molecular associations among the molecules in solution. To understand the relaxation behavior of 4-Nitroacetanilde in the dilute solution of carbon tetrachloride in microwave frequency region, the experiments are done at  various weight fractions and temperatures.

Experimental

4-Nitroacetanilide used in this investigation was purchased from the Central Drug House, Delhi. Carbon tetrachloride was procured from Merck and was used as a solvent without any further purification. The measurements of ε′ and εʺ are done by using X-Band microwave bench. The samples are prepared by dissolving five different mole fractions (0.01, 0.015, 0.02, 0.025, and 0.03) of 4-Nitroacetanilide in 1 mole of carbon tetrachloride. The values of (εʹ, εʺ, ε₀ and ε_∞) help to find the values of different relaxation times of samples in the solution. The dielectric relaxation studies suggest that the dielectric relaxation process depends on solute-solute association. The energy activation parameter (∆F_ε) for dielectric relaxation process is determined by using Eyring rate equation at various temperatures.

The double minima method given by Heston et al,¹¹ for low loss liquid is used to determine the values of εʹand εʺ. According to this method, we can write:

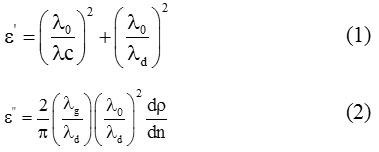
where

and

Here, λ₀ is the wavelength of free space, λ_c is the cut-off wavelength, λ_g is the wavelength in the empty waveguide and λ_d is the wavelength in the dielectric medium. ‘ρ’ denotes the inverse voltage standing wave ratio, ∆x represents double minima width and ‘ρ’ represents total number of minima. The accurateness of the measurements of the given X-band microwave test bench is ±0.01 cm. This helps to find error in the estimated values of dielectric constant. For simplicity, some errors caused by non-zero impedance of the short circuit plunger are ignored. We can measure these errors by using error analysis which is a conventional method to calculate such errors.¹² The values of dielectric permittivity at static frequencies (ε₀) are calculated by using dipole meter. Refractive indices are determined from Abbe’s refratometer which then gives the values of permittivity at optical frequencies (ε_∞).¹³

The dielectric parameters (εʹ, εʺ_, ε₀ and ε_∞) can be illustrated as a linear function of concentration for dilute solution in carbon tetrachloride. So they can be written as:

Here subscript 1 stands for pure solvent, 2 stands for the solute, 0 is for the zero frequency measurements in the static field and ∞ is for the values at very high frequency, W₂ represents the weight fraction of the solute. The slopes of these linear equations are denoted as aʹ, aʺ, a_o and a_∞ respectively.

The values of relaxation times (τ₁, τ₂ and τ₀) are determined by the method given by Higasi et al.,¹⁴

The relaxation time for overall molecular rotation (τ₁) is defined by:

While the relaxation time for intramolecular rotations (τ₂) is given by:

Here ‘ω’ is the angular frequency.

The most probable relaxation time (τ₀) is then obtained by employing the following relation:

The value of the dipole moment (μ) of the solute molecules is evaluated by using Higasi’s method. According to this method the value of dipole moment is given by:

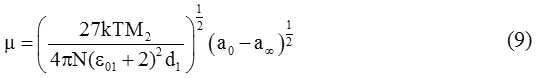
Where M₂ is the molecular weight of solute, d₁ is the density of solvent, k is the Boltzmann constant, N is the Avogadro’s number and T is the temperature at which the experiment is performed. Thus if the value of a₀ and a_∞ are known, we can obtain μ from equation (9) at different temperatures.

The temperature dependence characteristics of relaxation time can be used to determined different thermo dynamical parameters like molar free energy of activation (∆F_ε), molar enthalpy (∆H_ε) and molar entropy (∆S_ε).

From the Eyring theory the relaxation time can be represented as:

In which

Where A=h/k and the other symbols have their usual meanings

Taking logarithm on both side of equation (10), we get

By knowing the value of T and τ, we can calculate the value of ∆F_ε

From equation (10) and (11), we get.

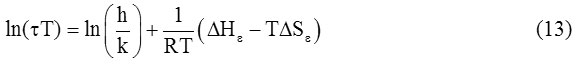
When a graph is plotted between ln(τT) and 1/T, a straight line is obtained. When its slope is multiplied by R, it gives the value of ∆H_ε.

Now by knowing the values of ∆F_ε and ∆H_ε , we can calculate the value of ∆S_ε by using the following relation.

Now for the viscous flow process Eyrings equation¹⁵ is given by

Where

Where B=hN/V and V is the molar volume which is equal to M/d. Here M is the molecular weight and d is density and η is the viscosity of the non polar solvent at temperature T K.

Taking logarithm on both the sides of (15), we get.

Knowing the values of η, V and T, ∆F_η  can be calculated.

From equation (15) and (16), we may get

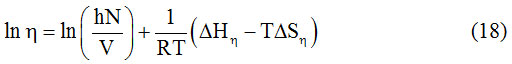
Plot of ln η against 1/T gives a straight line whose slope (∆H_ε/R) is when multiplied by gas constant ‘R’ gives the value of ∆H_η

Knowing ∆F_η  and ∆H_η, ∆S_η can be calculated from the following equation.

Result and Discussion

In the present study, dielectric investigations are done for 4-Nitroacetanilide using carbon tetrachloride as a solvent. The permittivity at optical frequency (ε_∞), permittivity at static frequency (ε₀), dielectric loss factor (εʺ) and dielectric constant at microwave frequency (εʹ) for solutions of 4-Nitroacetanilide with carbon tetrachloride are measured at different mole fractions and different temperatures and mentioned in Table: 1.This table shows that εʹ, εʺ ε₀ and ε_∞ are varying linearly with the weight fraction of 4-Nitroacetanilide in dilute solution of carbon tetrachloride.  It indicates that the entities of rotating molecules do not change their nature in the solution of carbon tetrachloride.¹⁶ The variation of these dielectric parameters with weight fractions are mentioned in Figures: 2, 3, 4 and 5. a′, aʺ, a₀ and a_∞ are the slope values of these plots and listed in Table: 2. These slope values help to determine the values of different relaxation times (τ₁, τ₂ and τ₀) and dipole moment (μ) which are listed in Table: 3. From this table we can see that the values of τ₁ and τ₂ are falling steadily with the rise in temperature in solution and such type of behavior may occurs due to the increased dipole size and molar volume with temperature.¹⁷ From Table: 3 also shows that the observed  values of intramolecular rotations are significantly higher than overall molecular rotation and this significant difference in the values of τ₁ and τ₂ represents the existence of more than one mechanism in the solution which shows that an additional intramolecular relaxation process exist along with the overall relaxation process in solution.¹⁸ It also indicates the dominance of intramolecular rotations over intermolecular rotations in solution. In the present study, the value of τ₀ is also found to decrease with the temperature of the solution.  From Table: 3, we can see that the dipole moments values are increases with the increase in temperature. This change in the dipole moment values may occur due to the stretching in band moment and change in the bond angle.¹⁹

For the solution of 4-Nitroacetanolide with carbon tetrachloride, we observed a linear relation graphically between ln(τT) & (1/T) (Figure: 6)  and ln(η) & (1/T) (Figure: 7) which shows that relaxation time values decaying exponentially with temperature in both  dielectric relaxation process and viscous flow processes. The values of ∆F_ε, ∆H_ε and ∆S_ε are evaluated by Eyring’s equation and the values of ∆F_η, ∆H_η and ∆S_η are evaluated by considering that the viscous flow process is also a rate process. These values of energy parameters for the dilute solution of 4-Nitroacetanolide with carbon tetrachloride at different temperatures is mentioned in Table: 4. From the present investigation, it is found that that we can treat both the process as a rate process.

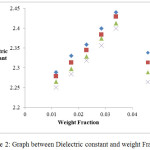Figure 2: Graph between Dielectric constant and weight Fraction. Click here to View figure

 

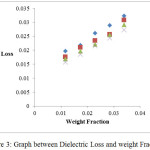Figure 3: Graph between Dielectric Loss and weight Fraction. Click here to View figure

 

Figure 4: Graph between Dielectric Permittivity at static Frequency and different Weight Fraction. Click here to View figure

 

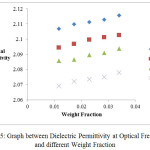Figure 5: Graph between Dielectric Permittivity at Optical Frequency at different Weight Fraction. Click here to View figure

 

Table: 2 Values of Slopes aʹ, aʺ, a_o and a_∞ for 4-Nitroacetanilide in the dilute solution of carbon tetrachloride at four different temperatures 9.27 GHz using X-Band microwave bench.

Temperature	a′	aʺ	a0	a∞
303	6.623	0.578	6.765	0.366
313	6.621	0.556	6.743	0.367
323	6.618	0.539	6.728	0.366
333	6.613	0.521	6.712	0.365

 

Table 3: Values of different relaxation times (τ_1, τ₂ and τ_o in pico sec.) and Dipole moment (μ in Debye) of 4-Nitroacetanilide in the dilute solution of Carbon tetrachloride at four different temperatures using X-Band microwave bench.

Temperature	τ0	τ1	τ2	μ
303	2.59	1.59	4.23	2.45
313	2.40	1.53	3.78	2.49
323	2.28	1.48	3.51	2.53
333	2.16	1.43	3.27	2.56

 

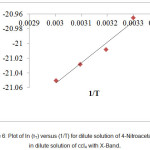Figure 6: Plot of ln (τT) versus (1/T) for dilute solution of 4-Nitroacetanilide in dilute solution of ccl4 with X-Band. Click here to View figure

 

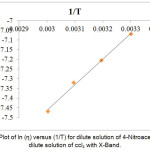Figure 7: Plot of ln (η) versus (1/T) for dilute solution of 4-Nitroacetanilide in dilute solution of ccl4 with X-Band. Click here to View figure

 

Table 4: Experimental Values of Energy Activation Parameters (∆F_ε, ∆H_ε and ∆S_ε) for dielectric relaxation Process and Energy Activation Parameters (∆F_η, ∆H_η and ∆S_η) for Viscous Flow Process in (cal/Mol) of 4-Nitroacetanilide in the dilute solution of Carbon tetrachloride at four different temperatures using X-Band microwave bench.

Temperature	∆Fε	∆Hε	∆Sε	∆Fη	∆Hη	∆Sη
303	1676.49	553.31	-3.71	3196.64	2618.46	-1.908
313	1705.06		-3.68	3218.43		-1.917
323	1746.64		-3.69	3247.85		-1.948
333	1786.30		-3.70	3251.33		-1.900

 

Conclusion

In the present paper, values of different dielectric parameters, dielectric relaxation times and activation energies have been  calculated and discussed  for the dilute solution of  4-Nitroacetanilide with carbon tetrachloride at various temperatures and mole fractions using standard methods.  The dielectric parameters are varying with the weight fractions of the solute in carbon tetrachloride. The values of relaxation times show the presence of more than one relaxation process in the system. The variation of dipole moment values with temperature may be due to the increase in the size of dipole. The values of the energy parameters for the dielectric relaxation process and for the viscous flow process are measured and compared which suggest that the dielectric relaxation process may be treated as a rate process just like the viscous flow process.

Acknowledgement

The authors are thankful to the Vice Chancellor, The IIS University for providing the necessary facilities for this work.

References

1. Chemical Book
2. Dyes and Dye Intermediates” in Kirk‑Othmer Encyclopedia of Chemical Technology, Peter Gregory
3. Gedam, S. B.; Suryavanshi, B. M. Int. J. Appl. Phys & Maths. 2013, 3, 302.
   CrossRef
4. Khan, A. M. A.; Subramanian, M. Int. J. Innov. Res. sci. Eng. Technol. 2014, 3, 16014.
5. Subramanian, M.; Sathish. Int. J. of Scientific Research & Education. 2016, 4, 4810.
6. Thakur,  N.; Sharma, D. R.  Ind. J. Pure & Appl. Phys. 2000, 38, 328.
7. Vyas, A. D.; Rana, V. A.; Ind. J. Pure & Appl. Phys. 2002, 40, 69.
8. Choudhary, A.; Ahire, S.; Mehrotra S. C.; J. Mol. Liq. 2001, 94, 17.
   CrossRef
9. Rewar, G. D.; Bhatnagar, D. Ind. J. Pure & Appl. Phys. 2002, 40, 430.
10. Sharma, V.; Thakur, N.; Sharma, D. R.; Negi, N. S.; Rangra, V. S. Ind. J. Pure & Appl. Phys. 2007,  45,163.
11. Heston, W. M.; Franklin, A. D.; Hennelly, E.J.; Smyth, W.P., J. Amer. Chem. Soc. 1950, 72, 3443.
    CrossRef
12. Fishbeck, H. J.; Fischbech, K. H.  Formula, facts and constants (Springer-Verlag, USA) 1987.
13. Aggaraval, C.; Arya, R.; Gandhi, J. M.; Sisodia, M. L. J. Mol liq. 1990, 44,161.
14. Higasi, K. Bull Chem Soc. 1966, 39, 2157.
    CrossRef
15. Glasstone, S., K. J. Laidler and H. Eyring (1941) The Theory of Rate Process, p. 611, McGraw Hill, New York.
16. Jain, R.; Bhargava, N.; Sharma,,K..S.; Bhatnagar, D. Ind. J. Pure & Appl. Phys. 2011, 49, 401.
17. Jain, R.; Bhargava, N.; Sharma, K. S.; Bhatnagar, D.  Int. J. Sci. Environ. Technol. 2013, 2, 416.
18. Ganesh, T.; Maria Sylvester, M.; Bhuvaneswari, S.; Jeevanantham, P.; Kumar, S. J. appl. Phys. 2014, 6, 59.
19. Nemmaniwar, B. G. Int. Res. J of. Science. & Engineering. 2017, 5,31.
20. Kalaivani, T.; Krishnan, S. Ind. J. Pure & Appl. Phys. 2009, 47, 383.
21. Singh, A. K. J. ultra sci. phys.sci. 2017, 29,171.
22. Kumar, R.; Rangra, V. S.; Sharma, D. R.; Thakur, N.; Negi, N. S. Z. Naturforsch. 2006, 61a, 197.
23. Kumar, R.; Kumar, R.; Rangra, V. S. Z. Naturforsch. 2010, 65a, 141.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.