Enhancing the Light Harvesting Efficiency, open Circuit Voltage and Stability of Molybdenum Doped (Zno)₆ Nanocluster in Dye-Sensitized Solar Cells: A DFT Study

Introduction

Nanostructured materials are currently of prodigious attention due to their reduced dimensions and are majorly take part in a large number of new devices. Among the renewable energy sources, solar energy is the favorable and sustainable alternative. Several photovoltaic devices are manufactured on II-VI semiconductor nanostructures.^1,2 Dye-sensitized solar cells (DSSC) are the real replacement to the well established silicon-based solar cells owing to their greater incident photon to current conversion efficiency, low cost, ease of device fabrication and durable stability.  The DSSCs are hinged on the absorption of photon energy over wide ranges and dye sensitizers. The π conjugated elements are used to stimulate the photosynthesis because of their electrochemical properties.³ Recently, the evolution of ZnO nanomaterials are growing exponentially, which was proven by the ZnO related papers in the literature.^4,5 The ZnO is a semiconductor metal oxide with broad energy gap has a higher probability in field effect transistors, solar cells, gas sensors, photodetectors, photocatalysts and optoelectronics due to its higher excitation binding energy.^6,7 The ZnO nanomaterials have replaced the bulk materials through their nanomorphology, functionality, low toxicity, good thermal stability, oxidation resistivity, biocompatibility, larger surface to volume ratio,  higher chemical reactivity, and greater electron mobility.^8,9 To extend the range of uses of ZnO nanomaterial, there are novel procedures to rephrase the electronic structures of ZnO such as depositing or doping various atoms in bulk ZnO materials experimentally and theoretically.¹⁰

The introduction of Mo atom into the ZnO material is an elemental reach to refine the properties of the host material.¹¹ Doping mechanism is the introduction of substitutional impurity by replacing single Zn atom by single Mo atom or single O atom by single Mo atom of the Zn₆O₆ at any position causes the significant upgrade in optoelectronics successfully.^12,13 The n-type Zn₆O₆ semiconductor material doping with an element of group VI as Mo, its physical properties can be tuned finely. Mo plays an essential character in the modern semiconductor industry and it is a predominant doping material to upgrade the performance of ZnO nanostructured materials. Recently, Chang-Lin Yu et.al.,¹⁴ has prepared Mo-doped ZnO photocatalysts by a grinding calcination method. They analyzed that, the Mo doping provided higher photocatalytic activity and stability than pure ZnO nanoparticles. R. Swapna et. al.,¹⁵ and V. Gokula Krishnan et. al.,¹⁶ have studied Mo-doped ZnO thin films by using the spray pyrolysis technique. They showed that the films have shown minimum resistivity, maximum carrier concentration and high electrical conductivity upon Mo doping.

In the present work, the Mo-doped Zn₆O₆ nano-cluster was studied and compared with its pristine form through energy, geometry, binding site, electronic properties, HOMO/LUMO energies, Mulliken charge distribution, DOS spectra, simulated IR, UV-Vis spectra and molecular electrostatic potential. A challenging way to inscribe this study is to utilize DFT and TD-DFT computational methods.¹⁷ The achievement of the solar cells was strengthened by the π conjugated system of the bridge. The structural unit of dyes is represented as D-π-A system. The Zn₆O₆ interacts with Mo which intensifies the light harvesting efficiency, open circuit voltage, the electron injection and the stability of solar cells. The MoZn₅O₆ material discovers extensive requirements in solar cells since an efficient photosensitizer which harvest the sunlight and retard the charge combination.

Computational Methods

Geometrical optimization of pure Zn₆O₆, Single Mo atom and MoZn₅O₆ were analyzed using density functional theory (DFT) method. The energy of HOMO (E_HOMO), the energy of LUMO (E_LUMO), and the energy gap (E_g = E_LUMO – E_HOMO) were investigated for pure Zn₆O₆ and MoZn₅O₆ using the hybrid density functional B3LYP and correlation functional of Lee- Yang- Parr with 6-31G and LANL2DZ basis sets using Gaussian 09 program.^18-20 For pure Zn₆O₆ and MoZn₅O₆ material, electronic states for a low spin as the singlet state (spin multiplicity = 1) were applied. To evaluate the excitation energy, UV-Vis electronic transition, light harvesting efficiency and oscillator strength of photosensitizers, TD-DFT calculations were employed at the CAM-B3LYP/6-31G level.  The density of states (DOS) for pure Zn₆O₆ and MoZn₆O₆ nanostructures were plotted by employing Gauss Sum Program.²¹ The determination of dipole moment, chemical parameters and polarizability were employed by the B3LYP/6-31G in Gaussian 09 program.²² In further, natural bond orbital (NBO) analysis, molecular electrostatic potential (MEP) analysis and Mulliken charge distribution of each atom in the title compounds were also implemented in the Gaussian 09 program. The thermodynamic parameters and the vibrational frequency were computed at the same level of theory.²³ The vibrational frequencies were evaluated to get all the structures are at a local minimum. Excited states analysis were performed using Time Dependent-Density Functional Theory (TD-DFT) Kohn-Sham equations in Gaussian 09 program.²⁴ The interaction between Mo and Zn₆O₆ cluster can be achieved by calculating binding energy as

E_B = E_Mo-Zn6O6 – E_Mo – E_Zn6O6                                (1)

Where E_Mo-Zn6O6 is the total energy of MoZn₅O₆ cluster, E_Mo is the total energy of the isolated Mo atom and E_Zn6O6 is the total energy of the isolated Zn₆O₆ cluster.²⁵ The negative value of the binding energy stipulates the exothermic process.²⁶

The energy gap E_g is defined as,

E_g = E_LUMO  – E_HOMO                                              (2)

Where, E_HOMO and E_LUMO are the energies of HOMO and LUMO, respectively. The energy shift ∆E_g was calculated as the ratio of the difference of E_g1 measured in pure Zn₆O₆ (reference value) and E_g2 measured in MoZn₅O₆ with respect to the reference value.²⁷

ΔE_g = [(E_g2 – E_g1) / (E_g1)]                                      (3)

The middle of the energy gap E_g is the chemical potential (µ). The chemical potential (µ) of free gas of electron is equal to its Fermi level. The Fermi level of MoZn₅O₆ was determined as the center of the energy gap E_g.²⁸

Results and Discussion

Structures and Stability

The optimized geometries of four isomeric structures of pure Zn₆O₆ nanocluster were obtained by using the Gaussian 09 program in the singlet ground state are shown in Fig. 1, whereas Fig. 2 represents the optimized drum structured Zn₆O₆ with MoZn₅O₆. The Zn₆O₆ nanocluster has four structural variants. Among all the structures, the properties of three-dimensional drum structured Zn₆O₆ have been scrutinized in this manuscript. The most known ZnO presentations are related to hexagonal forms and we expect that Zn₆O₆ nanocluster represents a superior potential source for further more research.²⁹ The structural data in the ground state and excited state of pure Zn₆O₆ and MoZn₅O₆ were listed in Table 1.

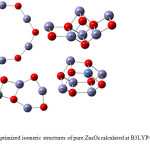Figure 1: The optimized isomeric structures of pure Zn6O6 calculated at B3LYP/6-31G level of theory. Click here to View figure

 

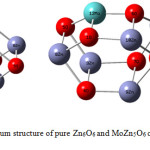Figure 2: The optimized drum structure of pure Zn6O6 and MoZn5O6 calculated at B3LYP/6-31G level of theory. Click here to View figure

 

Table 1: The calculated bond length of Zn₆O₆ and MoZn₅O₆ at B3LYP/6-31G in the ground state (Gnd) and excited state (Exc) analysis.

Bond distance	Zn6O6 (grd)	Zn6O6 (Exc)	Bond distance	MoZn5O6 at Zn(12) (grd)	MoZn5O6 at Zn(12)(Exc)
Zn(1)-O(2)	1.93	1.91	Zn(1)-O(2)	1.89	1.9
Zn(1)-O(7)	1.99	1.93	Zn(1)-O(7)	1.94	1.96
Zn(1)-O(9)	1.99	1.93	Zn(1)-O(9)	1.94	1.96
O(2)-Zn(10)	1.99	1.93	O(2)-Zn(10)	1.94	1.96
O(2)-Zn(12)	1.99	1.93	O(2)-Mo(12)	1.74	1.77
Zn(3)-O(4)	1.93	1.91	Zn(3)-O(4)	1.88	1.9
Zn(3)-O(8)	1.99	1.93	Zn(3)-O(8)	1.95	1.96
Zn(3)-O(9)	1.98	193	Zn(3)-O(9)	1.95	1.97
O(4)-Zn(10)	1.99	1.93	O(4)-Zn(10)	1.94	1.96
O(4)-Zn(11)	1.99	1.94	O(4)-Zn(11)	1.95	1.96
Zn(5)-O(6)	1.93	1.91	Zn(5)-O(6)	1.89	1.91
Zn(5)-O(7)	1.99	1.94	Zn(5)-O(7)	1.95	1.97
Zn(5)-O(8)	1.99	1.93	Zn(5)-O(8)	1.95	1.97
O(6)-Zn(11)	1.98	1.93	O(6)-Zn(11)	1.95	1.96
O(6)-Zn(12)	1.98	1.93	O(6)-Mo(12)	1.74	1.74
Zn(10)-O(9)	1.93	1.91	Zn(10)-O(9)	1.89	1.91
Zn(11)-O(8)	1.93	1.91	Zn(11)-O(8)	1.88	1.91
Zn(12)-O(7)	1.93	1.91	Mo(12)-O(7)	1.74	1.74

 

The nanostructure of drum structured pure Zn₆O₆ cluster has two hexagonal rings and six tetragons in the singlet ground state.³⁰ The symmetry of the Zn₆O₆ cluster is C₁ point group symmetry. Two different kinds of Zn-O bond lengths were identified within the pure Zn₆O₆. The bond distance of 1.93 Å was mutually shared between the two hexagons and the bond length of 1.99 Å was observed between the tetragon and a hexagon in DFT optimization. This bond length prediction is fine accordance with the Zn-O bond was calculated by Birajdar et. al.,³¹ and seetawan et.al.,³² depending on the structures of nanocluster. Results of TD-DFT the Zn-O bond length for pure Zn₆O₆ cluster between 1.91Å-1.93Å is fine agreement with the theoretical studies by wang et.al.³³ The charge transfer from the Zn atom to the O atom in pure Zn₆O₆ results the ionic bond of Zn-O. The bond angles of tetragons and the hexagons in the pure Zn₆O₆ cluster varied from 89º to 91⁰ and 116º to 124⁰. The calculated values of vibrational frequencies are positive from70cm^-1 to 716 cm^-1.

Analyzing the optimized structure of MoZn₅O₆, the bond distances of Zn-O bonds are increased in size when Mo replaced oxygen atoms at any position. The replacement of Zn by Mo at Zn (12) position favors the stabilization of the material by reducing bond distances in the singlet ground state is comparable to the work by Woodley et. al.³⁴ They showed Mg and Cd doping with pure ZnO nanoclusters to study their stability. The larger bond length difference occurs among the two hexagons at Zn(1)-O(7), Zn(10)-O(2), Zn(10)-O(4), Zn(5)-O(8) bonds to 1.88Å and the bond distance between the tetragon and hexagon of Zn(11)-O(8) reduced to 1.94Å. The bond distance of Mo(12)-O(7), Mo(12)-O(2), Mo(12)-O(7) was calculated as 1.74Å. Results of TD-DFT for Mo doping at Zn(12) position makes the changes in bond length at Mo(12)-O(2) increases to 1.77Å and Zn(5)-O(8), Zn(10)-O(2) to 1.96Å. The replacement of Zinc by Mo at Zn(10) brings the changes in bond distance among the hexagons as 1.91Å at Zn(1)-O(2), Zn(5)-O(6), Zn(10)-O(9) and the bond distance between the tetragon and a hexagon to 1.96Å at O(2)-Zn(10), Zn(5)-O(8) in the singlet DFT calculation. TD-DFT calculation brings the changes in Zn(10)-O(9) to 1.90Å and Zn(10)-O(2) to 1.95Å while Mo doping at Zn(10) position. The replacement of Zinc by Mo at Zn(3) and Zn(11) position elongates the bond distance among the two hexagons as 1.96Å and the bond distance connecting the hexagon and the tetragon as 2.01Å in the ground state and decreases at excited state analysis. The doping of Mo at Zn(5) and Zn(1) position produces a slight variation in the bond length than the pure cluster in both DFT and TD-DFT calculations. The huge difference in the bond length of Mo substituted structure and the pure form was observed at Zn (12) position of Mo doping in the singlet ground state. The interaction between Mo and the Zn₆O₆ nanocluster were studied by calculating the corresponding binding energy E_B as -1.76 Kcal/Mol. This calculation reveals that there were exothermic interaction with negative binding energy.³⁵

Frontier molecular orbital theory

The π type molecular orbital characteristics were exhibited by the HOMO/LUMO contours. The bonding behavior was specified by the HOMO orbital and the anti-bonding features were enumerated by the LUMO orbital. The HOMO/LUMO transition is identified as π – π^* intramolecular interaction.³⁶ Fig. 3 shows the distribution of HOMO and LUMO of pure Zn₆O₆ and MoZn₅O₆. The Zn atoms in the cluster have a positive charge which is an acceptor and O atoms have a negative charge which is the donor. The positive region appeared in green color and the negative region appeared in red color. The energies of HOMO and LUMO for pure Zn₆O₆ were -6.16eV and -2.89eV with energy gap E_g of 3.27eV was inadequate concurrence with the study done by Anitha et. al.,³⁷ The high energy gap of pure cluster indicates the thermal stability and inertness towards reactivity. It specifies that the electron in the valence band requires more energy to go to the conduction band. The larger energy gap makes the ZnO nanocluster applied in electronic devices.

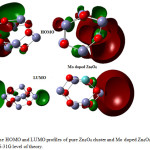Figure 3: The HOMO and LUMO profiles of pure Zn6O6 cluster and Mo doped Zn6O6 calculated at B3LYP/6-31G level of theory. Click here to View figure

 

After substitution with Mo, the HOMO levels are mostly scattered along the Mo doping region. The HOMO and LUMO describe the charge transfer between Mo and Zn₆O₆ cluster. The energies of HOMO and LUMO are changed to -4.64eV, -0.475eV and the energy gap is 4.16eV. ³⁸ The HOMO of the MoZn₅O₆ significantly shifted to the higher energies by -1.52eV. The photovoltaic properties of the above compound in solar cell applications were analyzed because of the extraordinary property of ZnO nanocluster as a shallow donor or acceptor.³⁹ The LUMO energy of the MoZn₅O₆ was higher than the conduction band (HOMO) of MoZn₅O₆, which predicts that this compound may be an effective candidate in a photovoltaic cell uses. The open circuit voltage of the organic solar cells is linearly related with the HOMO of the donor and LUMO of the acceptor.⁴⁰ The open circuit voltage V_OC was calculated by,

V_OC = │E_HOMO (Donor)│–│E_LUMO  (Acceptor)│ -0.3                                      (4)

The dye MoZn₅O₆ takes up the photon of energy which drives electrons to LUMO of the dye and then to the conduction band of MoZn₅O₆. The V_OC of pure Zn₅O₆ and MoZn₅O₆ were calculated to be 3.57eV and 4.46eV. The MoZn₅O₆ has high V_OC and the MoZn₅O₆ was used as efficient photosensitizers due to the good light absorption characteristics. All the methods of calculation used here are affirming that the energy gap of MoZn₅O₆ material is sensitive towards Mo doping. The energy gap values of Zn₆O₆ and MoZn₅O₆ were calculated at B3LYP/6-31G, B3LYP/6-311G, B3LYP/LANL2DZ has been listed in Table 2.

Table 2: The values of HOMO and LUMO energies (E_HOMO and E_LUMO), an energy gap (E_g) and the energy shift (∆E_g) of Zn₆O₆ and MoZn₅O₆ calculated at B3LYP/6-311G, 6-31G and the LANL2DZ level of theory.

System	Basis set	EHOMO (eV)	EFeV	ELUMO (eV)	Energy Gap Eg (eV)	∆EgeV
Zn6O6	B3LYP/6-31G	-6.16	-4.52	-2.89	3.27	–
MoZn5O6		-4.64	-2.79	-0.475	4.16	0.89
Zn6O6	B3LYP/6-311G	-5.94	-4.42	-2.79	3.14	–
MoZn5O6		-4.65	-2.58	-0.521	4.12	0.98
Zn6O6	B3LYP/LANL2DZ	-5.82	-4.27	-2.73	3.08	–
MoZn5O6		-4.89	-2.67	-0.469	4.42	1.34

 

Density of State Analysis

The density of states plot of pure Zn₆O₆ and MoZn₅O₆ are shown in Fig. 4. The energy gap of pure Zn₆O₆ was determined as 3.27eV. The energy gap MoZn₅O₆ was calculated as 4.16eV. By comparing the HOMO and LUMO levels of the pure Zn₆O₆ and MoZn₅O₆, the doping process causes the significant shift of HOMO of pure Zn₆O₆ to higher energy levels and the new HOMO of MoZn₅O₆ lies between the HOMO and LUMO of the pure Zn₆O₆. The DOS plot of MoZn₅O₆ indicates that Mo atom significantly participates in having a higher value of E_g and V_OC compared to the pure cluster. The Fermi energy (E_F) was increased after Mo doping and hence E_F shifts towards the conduction band. The E_F was increased from -4.52eV to -2.79eV after Mo doping. This increase in Fermi level assists the decrease in work function causes the MoZn₅O₆ material is an essential candidate in field emission. After the Mo substitution over the Zn₆O₆ nanocluster, Mo enhances the V_OC of MoZn₅O₆ by increasing the energy gap compared to the pure Zn₆O₆ cluster. Therefore, the MoZn₅O₆ material was found remarkable applications in solar cell devices.

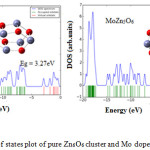Figure 4: The density of states plot of pure Zn6O6 cluster and Mo doped Zn6O6 nano material. Click here to View figure

 

Charge Population Analysis

Mulliken atomic charge distribution affords the information about the electron population of atoms in Zn₆O₆ and MoZn₅O₆ cluster. The Mulliken charge values were calculated from B3LYP/6-31G basis set. The Mulliken atomic charges of individual atoms present in Zn₆O₆ and MoZn₅O₆ are given in Table 3. For a pure Zn₆O₆ cluster, Zn1, Zn3, Zn5, Zn10, Zn11, and Zn12 atoms possess positive charges which are acceptor atoms and the atoms O2, O4, O6, O7, O8, and O9 own negative charges which are donor atoms. The oxygen atom (O7) in Zn₆O₆ has a more negative charge which is a donor. The Zinc atom (Zn10) has a more positive charge which is an acceptor. For MoZn₅O₆, Zn1, Zn3, Zn5, Zn10, Zn11, and Mo12 atoms possess positive charges which are acceptor atoms and the atoms O2, O4, O6, O7, O8, and O9 hold negative charges which are donor atoms.⁴¹ The Zn1 atom manifests more positive charge with a value 0.973e and O7 atom manifests more negative charge with a value 0.972e. The Mulliken atomic charge distributions of pure Zn₆O₆ and MoZn₅O₆ have been presented in Fig. 5. The NBO charges of pure Zn₆O₆ and MoZn₅O₆ in the singlet ground state are also shown in Table 3. In MoZn₅O₆, the charge transfers from the dopant Mo to the remaining part of the material as compared with the atomic charge of Zn atom of undoped Zn₆O₆. The metal dopant atom Mo acts as an electron acceptor.

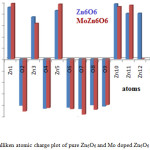Figure 5: Mulliken atomic charge plot of pure Zn6O6 and Mo doped Zn6O6 nano cluster. Click here to View figure

 

Table 3: Mulliken atomic charges (Mul) and NBO charges of Zn₆O₆ and MoZn₅O₆ calculated at B3LYP/6-31G.

Atom	Zn6O6 (Mul)	MoZn5O6 (Mul)	Zn6O6 (NBO)	MoZn5O6 (NBO)
Zn1	0.905	0.972	1.6	1.379
O2	-0.817	-0.917	-1.419	-1.232
Zn3	0.735	0.622	1.503	1.432
O4	-0.869	-0.857	-1.515	-1.482
Zn5	0.849	0.959	1.404	1.483
O6	-0.851	-0.877	-1.524	-1.231
O7	-0.875	-0.971	-1.475	-1.136
O8	-0.808	-0.887	1.517	-1.438
O9	-0.83	-0.805	-1.512	-1.272
Zn10	0.964	0.915	1.469	1.457
Zn11	0.797	0.94	1.593	1.414
Zn12	0.8	0	1.392	0
Mo	0	0.905	0	0.625

 

Analysis of Chemical parameters

The ionization potential (I), electron affinity (A), chemical hardness (η), chemical softness (S), chemical potential (µ), and electrophilicity index (ω) of MoZn₅O₆ were determined and compared with the pure Zn₆O₆ cluster and their values are tabulated in Table 4.The global reactivity descriptors were estimated from the energies of HOMO and LUMO to study the chemical stability and reactivity of MoZn₅O₆.

Table 4: Global Reactivity Descriptors of pure and MoZn₅O₆ calculated at B3LYP/6-31G.

Property	Zn6O6	MoZn5O6
I = -Eh eV	6.16	4.64
A = -El eV	2.89	0.475
Ƞ = (I – A)/2eV	1.63	2.08
µ = – (I + A)/2eV	-4.52	-2.55
Ψ = -µeV	4.52	2.55
S = 1/2ƞ eV	0.3	0.24
ω = µ2/2ƞeV	6.26	1.56
Dipole Moment	0.18	1.86
Polarizability	-92.08	-108.63
Hyper Polarizability	3.17	62.74

 

On the basis of Koopman’s theorem,⁴² the energies of HOMO (E_HOMO) and LUMO (E_LUMO) are associated with the ionization potential (I) and the electron affinity (A) as I = -E_HOMO and A = -E_LUMO. The ionization potential reduces when a Mo atom was substituted on Zn₆O₆ nanocluster. The ionization potential of the pure Zn₆O₆ was 6.16eV which declined to 4.64eV for MoZn₅O₆. The electron affinity decreases from 2.89eV to 0.475eV after Mo doping. This calculation correlated with Phool Singh Yadav et. al.,⁴³ as the ionization potential (I) was greater than the electron affinity (A). The chemical potential (µ) is defined based on the equation,

µ = – (I+A)/2                         (5)

The chemical potential (µ) increases for MoZn₅O₆ than its pure cluster. The calculated value of chemical potential (µ) for pure Zn₆O₆ was -4.52eV and -2.55eV for MoZn₅O₆. The Fermi level (E_F) of the MoZn₅O₆ is sited at the nucleus of the energy gap E_g. The chemical potential (µ) is also the middle point of the energy gap E_g, therefore Fermi level is similar to the chemical potential (µ). The electronegativity (Ψ) is the negative of the chemical potential (µ).

The chemical hardness (η) was calculated by,

η = (I – A)/2                          (6)

The chemical hardness (η) of Zn₆O₆ cluster was calculated as 1.635eV. The higher value of chemical hardness (η) in Zn₆O₆ predicts its rigid chemical stability. The chemical hardness (η) increases to 2.08eV after Mo substitution over the cluster. The chemical hardness (η) depends on the ionization potential (I) and electron affinity (A). The chemical softness (S) and the electrophilicity index (ɷ) are explained as,

S = 1/2ƞ                                                                               (7)

ω = µ²/2ƞeV                                                                        (8)

The chemical softness (S) is a perceptual of the chemical hardness (η). The chemical softness (S) of Zn₆O₆ was calculated as0.30eV. The chemical softness (S) decreases to 0.24eV when a Mo atom was substituted on the pure Zn₆O₆ cluster. The electrophilicity index (ɷ) of Zn₆O₆ was calculated as 6.26 eV and 1.56eV for MoZn₅O₆. The electrophilicity index (ɷ) computes the tendency of the material to accept electrons.

Analysis of NLO Parameters

The dipole moment is a salient electronic property which explains the charge distribution of the system. The calculated dipole moment for the pure cluster was found as 0.189 Debye and 1.867 Debye for MoZn₅O₆. The high value of dipole moment predicts the strong interaction among Mo and Zn₆O₆ cluster and it favors the greater NLO property. The polarizability and the first order hyperpolarizability were determined using DFT calculations.⁴⁴

The hyperpolarizability was expressed as,

µ = (µ_x²+µ_y²+µ_z²)^1/2                                                                         (9)

The total hyperpolarizability,

β_TOTAL = (β_x²+β_y²+β_z²)^1/2                                                             (10)

The mean polarizability,

<α> = 1/3(α_xx+α_yy+α_zz)                                                                   (11)

The calculated mean polarizability of pure Zn₆O₆ was -92.0865 Debye. The total hyperpolarizability of Zn₆O₆ was found to be 3.1712 Debye. The calculated mean polarizability of MoZn₅O₆ was -108.6326 Debye. The calculated total hyperpolarizability of MoZn₅O₆ was 62.74Debye. The highest contribution of the α_zz component indicates, the pure and Mo-doped Zn₆O₆ cluster elongated towards the Z direction and contracted to the X direction. The β_xzz component contributes with a larger part of hyperpolarizability in the pure form with the value 9.6624. The β_xxy component contributes more towards the hyperpolarizability of MoZn₅O₆ with the value 20.0258.  The MoZn₅O₆ material is a captivating gadget for further research of nonlinear optical properties due to the doping of the Mo atom.

Thermodynamic parameters:

The thermodynamic parameters of pure Zn₆O₆ and MoZn₅O₆ are displayed in Table 5. The thermal capacity (C_V) of MoZn₅O₆ was increased to 45.07 Cal/Mol-Kelvin from 43.86 Cal/Mol-Kelvin as compared to Zn₆O₆ cluster. The C_V shows that, the thermal capacity of the Zn₆O₆ and MoZn₅O₆ at room temperature and constant volume. The value of zero-point vibrational energy of Zn₆O₆ and MoZn₅O₆ were found to be 16.77 and 15.94 Kcal/Mol. The change in enthalpy (ΔH), the change in entropy (ΔS) and the change in Gibbs free energy (ΔG) of pure Zn₆O₆ and MoZn₅O₆ were computed from the frequency calculations using the consequent equations,

ΔH = H_Mo-Zn6O6 – H_Mo – H_Zn6O6                                      (12)

ΔS = S_Mo-Zn6O6 – S_Mo – S_Zn6O6                                                  (13)              

ΔG= G_Mo-Zn6O6 – G_Mo – G_Zn6O6                                               (14)

Where, H_MoZn5O6, H_Zn6O6, and H_Mo are the sum of electronic and thermal enthalpies of Zn₆O₆, MoZn₅O₆, and Mo atom. G_MoZn5O6, G _Zn6O6, and G_Mo are the sum of electronic and thermal free energies of Zn₆O₆, MoZn₅O_6, and Mo atom. S _MoZn5O6, S_Zn6O6, and S_Mo are the entropies of Zn₆O₆, MoZn₅O_6, and Mo atom.⁴⁵ The values of ∆H, ∆S and ∆G were calculated as 65.4454, 38.078 and 65.4239Cal/M-Kelvin.

Table 5: The thermodynamic parameters of pure Zn₆O₆ and MoZn₅O₆ calculated at B3LYP/ 6-31G.

Thermodynamic Parameters	Zn6O6	MoZn5O6
Total energy (Thermal), Etotal (Kcal/mol	24.56	23.68
Vibrational energy, Evib(Kcal/mol)	22.78	21.91
Zero points vibrational energy (Kcal/mol)	16.77	15.94
Rotational constants (GHz)
X	0.484	0.472
Y	0.342	0.305
Z	0.295	0.268
Specific heat Cv (cal/mol/K)	45.07	43.86
Entropy S (cal/mol/K)	112.41	113.99
Zero point correction (Hartee/particle)	0.026	0.025
Thermal correction to energy	0.039	0.038
Thermal correction to the enthalpy	0.04	0.038
Thermal correction to Gibbs free energy	-0.013	-0.015

 

Molecular electrostatic potential

Molecular electrostatic potential (MEP) predicts the three-dimensional charge distribution of Zn₆O₆ and MoZn₅O₆. All isosurfaces are depicted with isovalue of 0.0004e/au³ in Gauss view software.⁴⁶ MEP plot offers the positive and the negative region of Zn₆O₆ cluster and MoZn₅O₆ are shown in Fig. 6. In Fig. 6a, the Zn atoms were positively charged which are present in blue color. The O atoms were negatively charged which are appeared in red color. This reveals that there is the charge transfer from Zn atoms to O atoms which results in ionic bonds in the Zn₆O₆ nanocluster. In Fig. 6b, based on the MEP calculation upon MoZn₅O₆ cluster, the Zn atoms were specified by red color shows negative in charge. This confirms that there is a charge transfer from Mo doping material to the nanocluster because of the strong interaction. The total charge of MoZn₅O₆ material was -1.0. MEP surface prompted by the charge distribution of Zn₆O₆ and MoZn₅O₆ at an atomic site is described as,

 

 

Where Z_A is the charge on nucleus A located at R_A .⁴⁷

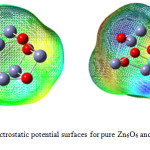Figure 6: Molecular electrostatic potential surfaces for pure Zn6O6 and Mo substituted Zn6O6 nano cluster. Click here to View figure

 

Vibrational analysis

The vibration frequencies were the unique parameter to explore the local minimum in structures. The theoretical FTIR spectra of Zn₆O₆ and MoZn₅O₆ were presented in Fig. 7. Transmittance is the principal features of Zn-O vibration.⁴⁸ There are 30 possible modes of vibrations in pure Zn₆O₆. The simulated IR spectrum of pure Zn₆O₆ shows the absorption peaks at 430cm^-1, 451cm^-1 and 547cm^-1 have corresponded to the Zn-O stretching vibrations.^49,50

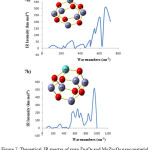Figure 7: Theoretical IR spectra of pure Zn6O6 and MoZn5O6 nano material. Click here to View figure

 

Sowbagya et. al.,⁵¹ have synthesized Mo-doped ZnO nanoparticles and studied the FTIR spectrum. They showed that the Zn-O stretching vibration was observed at 443 cm^-1. The existence of Mo-O₃ depicted with the peak around 556cm^-1, 859cm^-1 and 617cm^-1.  The stretching vibration of Mo=O was observed at 925cm^-1. In this present theoretical investigation, the Mo-doped Zn₆O₆ exhibits 30 modes of vibrations. The peak at 438 cm^-1 was assigned to the stretching vibration of the Zn-O bond. The peaks at 533cm^-1, 606cm^-1 and 842cm^-1 were assigned to the various bonds of Mo(12)-O(2), Mo(12)-O(6) and Mo(12)-O(7) respectively. The absorption band at 952cm^-1 indicating the Mo=O stretching vibration. The presence of additional absorption bands from 438cm^-1 to 1001cm^-1 indicates the existence of Mo and its oxides.

Absorption Spectra and Photovoltaic properties:

The UV-Vis spectra of pure Zn₆O₆ and MoZn₅O₆ were analyzed and the wavelength (λ_max), excitation energies (∆E) and oscillator strength (f) were computed using the singlet excited state at the B3LYP/6-31G by the time-dependent density functional theory calculations (TD-DFT) and the results were listed in Table 6.

Table 6: The excitation wavelength (λ_max), excitation energies (∆E) and oscillator strength (f) of  Zn₆O₆ and MoZn₅O₆.

Compound	Excitations	Excitation wavelength (nm)	Oscillator strength (f)	Energy (eV)
Zn6O6	114 à115	578	0.6	2.14
	113 à115	565	0.42	2.19
	111 à115	531	0.15	2.33
MoZn5O6	60à  62	511	0.12	2.43
	60à  63	417	0.15	2.97
	60à  62	412	0.9	3

 

The high absorption of the Zn₆O₆ and MoZn₅O₆ were studied from the energy gap (E_g). The lowest singlet to singlet excited state transitions were investigated to study the electronic absorption mechanism in whole visible/near-IR regions. On the basis of Frank Condon principle, the maximum peak correlates with vertical excitation. The electronic excitation observed as π – π^* transitions. The energy gap of Zn₆O₆ cluster was 3.27 eV so that the λ_max was fall in the visible region. There are three peaks with excitation energies 2.14eV, 2.19eV, and 2.33eV for the pure Zn₆O₆. The excitation wavelengths (λ_max) of the absorption spectrum of Zn₆O₆ were determined as 578nm, 565nm, and 531 nm. The higher value of oscillator strength (f) was calculated as 0.60 with the excitation energy (∆E) of 2.14eV. After the Mo doping in Zn₆O₆ cluster, the excitation energies (∆E) were calculated as 2.43eV, 2.97eV, and 3eV. The higher value of oscillator strength (f) was calculated as 0.90 with the excitation energy 3eV. The MoZn₅O₆ materialis beneficent in increasing the light harvesting efficiency which leads to the higher short circuit current density (Jsc).⁵² The short-circuit current density (Jsc) is closely related to the charge conversion efficiency (η) of the solar cell can be calculated by the following equation,

Jsc = ∫LHE (λ) φ_Inject.η_collect dλ                                                 (16)

Where LHE (λ) is the light harvesting efficiency, φ_Inject is the electron injection efficiency to the conduction band of MoZn₅O₆ and η_collect is the electron collection efficiency. The φ_Inject is associated with the driving force ΔG_inject for the electron injection. The light harvesting efficiency LHE (λ) can be expressed as⁵³

LHE = 1-10^-f                                                                                                    (17)

Where f is the oscillating strength of the maximum absorption spectra of Zn₆O₆ and MoZn₅O₆.

The large φ_Inject leads to the higher Jsc. The φ_Inject is directly proportional to the free energy of electron injection as

φ_Inject α f (- ΔG^Inject)

ΔG^Inject = E^dye* – E_CB                                                          (18)

Where E^dye* represent the oxidation potential energy in the excited state and E_CB represent the reduction potential of the conduction band. E^dye* can be estimated by,

E^dye* = E^dye – ΔE                                                     (19)

Where E_dye represents the energy of oxidation potential in the ground state and ΔE is the energy of the electronic vertical transition corresponding to λ_max. The oxidation potential of the dye is directly related to the HOMO level and the driving force for the reduction of oxidized dye increase at the larger oxidation potential. The values of an electron injection (ΔG^Inject), oxidation potential (E^dye* and E_dye) and open circuit voltage (V_OC) of pure Zn₆O₆ andMoZn₅O₆ are summarized in Table 7.

Table 7: The values of an electron injection (ΔG^Inject), oxidation potential (E^dye* and E_dye) and open circuit voltage (V_OC) of pure Zn₆O₆ andMoZn₅O₆ calculated from UV_VIS absorption spectra.

System	Eg	VOC	Eoxdye(eV)	Eoxdye*(eV)	∆GInject	LHE
Zn6O6	3.27	3.57	2.14	2.33	3.83	0.75
MoZn5O6	4.16	4.46	2.43	3	1.64	0.87

 

Conclusion

The theoretical investigation on geometrical structures, binding nature, UV-Vis spectra, vibrational frequencies and the electronic properties of Zn₆O₆ andMoZn₅O₆ have been analyzed to predict the photovoltaic properties using DFT and TD-DFT theory. The doping of Mo makes the substantial modification in the HOMO and LUMO energies which ensures the open circuit voltage (V_OC) of the MoZn₅O₆ was higher than the pristine Zn₆O₆ cluster. The high open circuit voltage making MoZn₅O₆ as a potential compound in the photovoltaic applications and is also been an efficient sensitizer. The density of state analysis brings the light absorption characteristics of MoZn₅O₆ system expands consequently by the doping material. The calculations from the various basis sets predict that there was a significant charge transfer from the dopant to the pure cluster, which enhances the energy gap E_g. The nonlinear optical characteristic of MoZn₅O₆ material was studied by hyperpolarizability. The dipole moment of MoZn₅O₆ was higher than its pure form. The increase in light harvesting efficiency of MoZn₅O₆ was calculated from the electronic transition in UV-Vis spectra. The replacement of Mo assists the hexagonal MoZn₅O₆ nanomaterial has more photoresponse than Zn₆O₆ which would be a better potential originator in solar cell applications.

References

1. Gu, G. R., Ito, T., Field emission characteristics of thin metal coated nanosheet carbon films,  Applied Surface Science., 2011,  257, 2455-2460.
   CrossRef
2. Mackowski, S., Karczewski, G., Wojtowicz, Qju, X., Howe, J. Y., Mayer, H. M., Tuncer, E., Parantharaman, M. P., Thermal stability of HfO₂ nanotube arrays, Applied Surface Science, 2011, 257, 4057-4081.
3. Hagfeldt, A., Boschloo, G.,  Sun, L., Kloo, L., Pettersson, H., Dye-sensitized solar cells, Chem. Rev. 2010, 110 , 6595-6663.
   CrossRef
4. Wu, Y. L., Tok, A. I. Y., Boey, F. Y. C., Zeng, X. T., Zhang, X. H., Surface modification of ZnO crystals, Applied Surface Science, 2007, 253, 5473-5479.
   CrossRef
5. Prades, J. D., Cirera, A., Morante, J.R., Ab initio calculation of No₂ and So₂ chemisorption on to nonpolar ZnO surfaces, Sensors and Actuators B: Chemical, 2009, 142, 179-184.
   CrossRef
6. Duan, J., Huang, X., Wang, E., PEG-assisted synthesis of ZnO nanotubes, Material Letters, 2006,  60, 1918-1921.
   CrossRef
7.  Aslanzadeh, S., Transition metal-doped ZnO nanoclusters for carbon monoxide detection: DFT studies, J. Mol. Model, 2016, 22, 160.
   CrossRef
8. Abdulsattar, M. A, Chlorine gas reaction with ZnO wurtzoid nanocrystals as a function of temperature: a DFT study, J. Mol, Model, 2017, 23, 125.
   CrossRef
9. Patil, A. B., Patil, K. R., Pardeshi, S. K., Eco-friendly synthesis and solar photocatalytic activity of S-doped ZnO, J. Hazard. Mater., 2010, 183, 315.
   CrossRef
10. Song, T. M., Wang, T. H., Li, J. C., First-principles study of periodic size-dependent band gap variation of Cu doped ZnO single wall nanotube, J. Mol. Model, 2012, 18, 5035.
    CrossRef
11. Jianguang Wang, Li Ma, Yanhua Liang, Meiling Gao, Guanghou Wang, Density functional theory study of transition metals doped B₈₀ fullerene, J. Theor. Comput. Chem, 2014, 13, 1450050.
    CrossRef
12. Waranya Pipornpong, Benjawan Kaewruksa, Vithaya Ruangpornvisuti, DFT investigation on molecular structures of metal and non-metal doped ZnO sodalike cage and their electronic properties, Structural chemistry,  2016, 27, 773-784.
    CrossRef
13. Mokhtar hjiri, Lasaad El Mir, Salvator Gianluca Leonardi, Micola Donato, and Giovanni Neri, Co and No₂ selective monitoring by ZnO based sensors, Nano Materials, 2013, 3, 357-369.
14. Chang Lin Yu, Kai Yang, Qingshu, Jimmy C. Yu, Fang Fang Cao, Xin Li, Xiaochun Zhou, Preparation, Characterization and photocatalytic performance of Mo-doped ZnO photocatalysts, Science China Chemistry, 2015, 55, 1802-1810.
15. Swapna,  R., Santhosh Kumar, M. C., Growth and Characterization of Mo-doped ZnO thin films by spray pyrolysis, Journal of Physics and Chemistry, 2013, 74, 418-425.
16. Gokulakrishnan, V., Parthiban, S., Jeganathan, K., Ramamurthy, K., Investigation of Mo-doped ZnO thin films prepared by spray pyrolysis Technique, Ferroelectrics, 2011, 423, 126-134.
    CrossRef
17. Ali Shokuhi Rad, Comparison of X₁₂Y₁₂ ( X=Al, B and Y=N, P) fullerene-like nanoclusters toward adsorption of dimethyl ether, J. Theor. Comput. Chem., 2018, 17, 1850013.
    CrossRef
18. Becke A. D., Density functional exchange-energy approximation with correct asymptotic behavior, Physics Review A. 1988, 38, 3098-3100.
    CrossRef
19. Lee, C., Yang, W., Parr, R. G., Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Physics Review B, 1988, 37, 785-789.
    CrossRef
20. katarzyna pustule, Marcin Makowski, Assessing accuracy of exchange-correlation functional for electron affinities, J. Theor. Comput. Chem., 2017, 16, 1750052.
    CrossRef
21. O’Boyle, N. M., Tenderholt, A. L., Langner, K. M., “Cclib: a library for package independent computational chemistry algorithm”, J. Comput. Chem., 2008,  9, 839-845.
    CrossRef
22. Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., Scalmani, G., Barone, V., Mennucci, B., Peterson, G.A., Nakatsuji, H., Caricato, M., Li, X., Hratchian, H. P., Izmaylov, A. F., Bloino, J., Zheng G, Sonnenberg JL, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Vreven T., Montgomery, J. A., Jr, Peralta, J. E., Ogliaro, F, Bearpark, M., Heyd, J. J, Brothers, E., Kudin K. N., Staroverov, V. N., Kobayashi, R., Normand, J., Raghavachari, K., Rendell A., Burant, J. C., Iyengar, S. S., Tomasi, J., Cossi M., Rega, N., Millam, M. J., Klene, M., Knox, J. E., Cross, J. B., Bakken, V., Adamo, C., Jaramillo, J., Gomperts, R., Stratmann, R. E., Yazyev, O., Austin, A. J., Cammi, R., Pomeli, C., Ochterski, J. W., Martin, R. L., Morokuma, K., Zakrzewski, C. G., Voth, G. A., Salvador, P., Dannenberg, J. J., Dapprich, S., Daniels, A. D., Farkas, O., Foresman, J. B., Ortiz, J. V., Cioslowski, J., Fox, D. J., 2009, Gaussian, Inc., Wallingford C. T., 2009, Gaussian 09, Revision D.01, Gaussian, Inc Wallingford CT, 2009.
23. Ochterski,  J. W., Thermochemistry in Gaussian Inc. Pittsburgh, PA, 2000.
24. Manuel Alberto Flores Hidalgo, Diana Barraza Jimenez, Daniel glosman-Mitnik, Excited states analysis of sulfur substitutional impurities on (ZnO)₆ cluster using DFT and TD-DFT, Journal of molecular structure: Theochem, 2010, 957, 100-107.
    CrossRef
25. Ali Shokuhi Rad, Khurshid Ayub, Ni adsorption on Al₁₂P₁₂ nano cage: DFT study, J. Alloys. Comp. 2016, 678, 317-324.
    CrossRef
26. Fatemeh Fallahpour, Milad Nouraliei, sara Soleimani Gorgani, Theoretical evaluation of a double functional heterogeneous nano sensors, Appl. Surf. Sci, 2016, 366, 545-551.
    CrossRef
27. Saeed Aslanzadeh, Transition metal doped ZnO nanoclusters for carbon monoxide detection: DFT studies, J.Mol.Model, 2016, 22, 160.
    CrossRef
28. Hamid Salimi, Ali Ahmadi Peyghan, Maziar Noel, Adsorption of Formic acid and Formate anion on ZnO nano cage: A DFT study, J. Clustr. Science, 2013, 26, 609-621.
    CrossRef
29. Manuel Alberto Flores-Hidalgo, Diana Barraza-Jimenez, Daniel Glossman-Mitnik, Effects of sulphur substitutional impurities on (ZnO)_n clusters (n=4-12) using density functional theory, Comput. Theor. Chem, 2011, 965, 154-162.
    CrossRef
30. Nour El Houda Bensiradj, Amar Saal, Azeddine Dekhira, Quirda Quamerali, Theoretical study of selenium and tellurium impurities in (ZnO)₆ clusters using DFT and TD-DFT, Int. J. Quantum Chemistry, 2016, 116, 1823-1898.
31. Birajdar, S. D., Khirade, P. P., Bhagwat, V., Humbe, A. V., Jadhav, K., Synthesis, structural, morphological, optical and magnetic properties of Zn 1− x Co x O (0≤ x≤ 0.36) nanoparticles synthesized by sol gel-auto combustion method. Journal of Alloys and Compounds, 2016, 683, 513-526.
    CrossRef
32. Seetawan, U., Jugsujinda, S., Seetawan, T., Ratchasin, A., Euvananont, C., Junin, C.,             Thanachayanont, C., Chainaronk, P., Effect of calcinations temperature on crystallography and nanoparticles in ZnO disk. Mater. Sci. Appln, 2011, 2, 1302–1307.
    CrossRef
33. Zhong Lin Wang, nanostructures of ZnO, Materials today, 2004, 7, 26-33.
    CrossRef
34. Samson R Woodley, Alexy, A.,  Sokol, Richard, C., Catlow, A., Abdullah, A., Al-Sunaidi, Scott M. Woodley,  Journal of Physical Chemistry, 2013, 117, 27127-27145.
35. Fatemeh Fallahpour Milad Nouraliei, Sara Soleimani Gorgani, Theoretical evaluation of Double-functional Heterogeneous Nano-Sensor, App. Surf. Sci, 2016, 366, 545-551.
    CrossRef
36. Dheivamalar S, Sugi L, Density functional theory (DFT) investigation on doped fullerene with hetero atom substitution, Spectrochim. Acta Part A, 2015, 151, 687-695.
    CrossRef
37. Anitha, Varughese, Characterization, thermal effect on optical band gap energy and photoluminescence in wurtzite ZnO: Er nanocrystallites, J. Material processing Tech, 2015, 3, 145-151.
38. Wen Liu, Fan-Hua Meng, Jian- Hua Zhao, Xiao- Hui Jiang, A first principles study on the electronic transport properties of zig zag grapheme/grapheme nanoribbons, J. Theor. Compt. Chem., 2017, 16, 1750032.
    CrossRef
39. Pal, S., Sarkar, A., Shallow acceptor state in ZnO realized by ion irradiation and annealing route, J. alloys and Compounds, 2017, 703, 26-33.
    CrossRef
40. Abram, T., Chitra, S., Bejjit, L., Bouachrine, M., Lakhlifi, T., Electronic and photovoltaic properties of new materials based on 6-mono substituted and 3,6-disubstituted acridines and their application to design novel materials, for organic solar cells, J. Comp. Methods in Mol. Designs, 2014,  4, 19-27.
41. Chandraboss, V. L., Karthikeyan, B., Senthilvelan, S., Experimental and first principle study of guanine adsorption on ZnO clusters, Phys. Chem. Chem. Phys, 2014, 16, 23461.
    CrossRef
42. Koopmans, T., ordering of wave functions and eigen energies to the individual electrons of an atom, physica 1, 1933, 104-113
43. Phool Singh Yadav, Dheeraj Kumar Pandey, A DFT study for the structural and electronic properties of Zn_mSe_n nanoclusters, App.Nanosci., 2012, 2, 351-357.
    CrossRef
44. Dheivamalar, S., Sugi, L., Ambigai, K., Density functional theory study of exohedral carbon atoms effect on electrophilicity of nicotine: Comparative analysis, Comp. Chem, 2016, 4, 17-31.
    CrossRef
45. Masoud Bezi Javan, Alireza Soltani, Tazikeh Lemeski E, Afsaneh Ahmadi, Sahar Moazen Rad, Interaction of B₁₂N₁₂ nano cage with cysteine through various functionalities: A DFT study, Sup. Latt. Mic. Struc, 2016, 100, 24-37.
46. Gaussview 4.1.2, Gaussian Inc., Wallingford, CT, 2004.
47. Ali Shokuhi Rad, Khurshid Ayub, Detailed surface study of adsorbed nickel on Al₁₂N₁₂ nano cage, Thin solid films, 2016, 612, 179-185.
    CrossRef
48. Agarwal, D. C., SHI induced modification of ZnO thin film: optical and structural studies, Nucl. Instrum. Methods Phys. Res., Sect. B, 2006, 244, 136-140.
49. Wahab, R., Kim, Y. S., Hwang, I. H., Shin, H. S. A non aqueous synthesis, characterization of zinc oxide nano particles and their interaction with DNA, Synth. Met.  2009, 159, 2443-2452.
    CrossRef
50. Deneva, I. M., Infrared spectroscopy investigation of metallic nano particles based on copper, cobalt, and nickel synthesized through borohydride reduction method, J. Univ. Chem. Technol. Metall., 2011, 45, 351-378.
51. Sowbagya, Ananda, S., synthesis and characterization of Mo-doped ZnO nano particles by electrochemical method: Photodegradation kinetics of methyl violet dye and study of anti bacterial activities of MO- doped ZnO nano particles, International journal of nanomaterials and biostructures, 2015, 5, 7-14.
52. Mishra, A., Bauerla, P., Small Molecule Organic Semiconductors on the Move: Promises for Future Solar Energy Technology, Angew. Chem. Int. Ed., 2012,51, 2020-2067.
    CrossRef
53. Qin, C., Clark, A. E., DFT characterization of the optical and redox properties of natural pigments relevant to dye-sensitized solar cells, Chem.Phys.Let.,2007, 438, 26-30.
    CrossRef

---

This work is licensed under a Creative Commons Attribution 4.0 International License.