The QSPR Study of Butane Derivatives: A Mathematical Approach

Introduction

Butane is an organic compound with the formula C₄H₁₀ that is an alkane with four carbon atoms. Butane derivatives are chemical compounds formally derived from the parent compound Butane by the replacement of one or more hydrogen atoms with other atoms or functional groups. The study of the quantitative structure activity/property relationships of compounds is a relevant approach of modern chemistry because of the details obtained consists of mathematical equations correlating the chemical structure of the compounds to a large variety of their physical, chemical and biological properties. Hence by modeling and finding structure-property relationship of physiochemical properties of Butane derivatives with the topological parameters we can even predict the existence of more products of Butane which are unknown. In this study, we use the physiochemical properties of Butane derivatives taken from PubChem.¹

Materials and Methods

The QSPR study was performed on the data set consisting of fourteen Butane derivatives. Butane derivatives of our concern are all acyclic compounds except one which contain Benzene in their molecular structure. A topological portrayal of a molecule can be brought out through molecular graph representation. Topological index is a numerical value estimated from the molecular graph. In this study, the Butane derivatives are represented as graphs, where each vertex of graph represents an element and each edge denotes a chemical bond between two elements. Specifically, we use hydrogen suppressed molecular graph structures to compute topological indices of Butane derivatives. As it is the convention, only single bonds between elements are considered. The molecular descriptors we studied are Weiner indices,² Harary indices,³ Balaban index,⁴ Zagreb indices^5-7 and Eccentric indices.^8-11 However, we present here only four of them. Let d_G(u, v) be the distance between the vertices of the u and v in the graph G. Let d(u) be the degree of the vertex u of a graph G. Then we have the following indices.

The Redefined Zagreb Indices

ReZG₁(G)= Σ(d(u)+d(v))/(d(u)d(v)),¹² for all edges uv of the graph G.           (1)

ReZG₃(G)=Σ(d(u)d(v)) (d(u)+d(v)),¹² for all edges uv of the graph G.            (2)

In 2013, the redefined versions of Zagreb indices¹² were introduced. Since then, more focus is on structural computations of these indices. The indices of numerous chemically important compounds such as graphene and various nanostructures were computed.^13-18 It is found that no studies are conducted on the correlation between the physiochemical properties of compounds with the molecular descriptors.

The Reformulated Zagreb Index

EM₁(G)= Σ(d(uv)),¹⁹ for all edges uv of the graph G.                 (3)

The Reformulated first Zagreb index was introduced in 2004 by Miličević, Nikolić and Trinajstić.¹⁹ Most of the articles on the Reformulated Zagreb index discuss on the various properties of Reformulated first Zagreb index such as lower and upper bounds.^20-24 Many works are on the computation of the index of various compounds and of certain class of graphs.^23,25-32 It has been mentioned that, among all the versions of the Zagreb indices, the Reformulated first Zagreb index has a significant role in QSPR study.³³ Nevertheless, since its inception, no QSPR/QSAR study on Reformulated Zagreb index is found in the literature.

The Sum Connectivity Index

χ(G)= Σ1/√(d(u)+d(v)),³⁴ for all edges uv of the graph G.           (4)

The Sum connectivity index³⁴ introduced in 2009 has a major role in the QSPR studies. It has been found that the sum connectivity index has a close correlation with various physiochemical properties of alkanes such as boiling point, molar volume, molar refraction, heat of vaporization, surface tension and melting point.^30,35-42 Therefore, there is a probability of having a correlation between more physiochemical properties. In our study, we found that the sum connectivity index has a close correlation with the Hydrogen bond acceptor count of the Butane derivatives. Hence, this paper on the QSPR study of Butane derivatives with the Reformulated, Redefined Zagreb indices and Sum connectivity index is a foundation for the future QSPR investigations on these topological indices.

Results and Discussions

The significance of the QSPR analysis is that it relates the molecular structure of the compound to a numerical value which helps in obtaining the physiochemical properties of compounds.^43-45 The various indices of fourteen Butane derivatives are obtained from the molecular graphs of Butane derivatives. In fact we initially studied more than 30 indices. We then focused our attention to the Redefined first Zagreb index, the Redefined third Zagreb index, the Sum connectivity index and the Reformulated first Zagreb index. The graphs are plotted between the topological parameters and the physiochemical values of the compounds using Origin. We find correlations between the molecular descriptors and physiochemical properties of Butane derivatives.Table 1 is used in generating the plots of results.

Table 1: Butane derivatives with the molecular properties and Descriptors.

	Compound	HBAC	χ(G)	Complexity	ReZG3(G)	HAC	ReZG1(G)	Surface tension	EM1(G)
1	1,4-butanedithiol	2	2.6547	17.5	60	6	6	31.1	14
2	2-butanone	1	2.02456	38.5	60	5	5	22.9	7
3	1,3-butanediol	2	3.4167	28.7	76	6	6	34.9	22
4	butane dinitrile	2	2.6547	92	76	6	6	40.7	14
5	butanediamide	2	3.809	96.6	124	8	8	53	38
6	butane-1-sulfoamide	3	3.3272	133	146	8	6.4	41.9	45
7	1-butanethiol	1	2.15470	13.1	44	5	5	24.8	10
8	1,4-diaminobuane	2	2.645	17.5	60	6	2.33	35.8	14
9	butane-1,4-disulfonic acid	6	4.9997	266	216	12	12	77.9	84
10	butyraldehyde	1	2.1547	24.8	44	5	3.33	23.1	10
11	2,3-butanedione	2	2.40825	71.5	92	6	6.66	27.3	20
12	butanedihydrazide	4	4.44355	119	154	10	10.5	59	50
13	1-butanesufonylchloride	2	3.3272	133	60	8	2.33	36.4	45
14	butyl-2-benzene	0	5.154	80	152	10	9.66	29	64

 

We see that there are correlations between some of the properties of Butane derivatives with the corresponding topological indices. Among all the properties, we find that Heavy atomic count, Hydrogen bond acceptor count, Complexity and Surface tension of butane derivatives have close correlation with the Redefined first Zagreb index, Sum connectivity index, Redefined third Zagreb index and Reformulated first Zagreb index, respectively. Following are the plots giving these correlations.

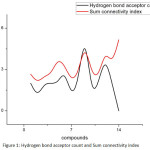Figure 1: Hydrogen bond acceptor count and Sum connectivity index. Click here to View figure

 

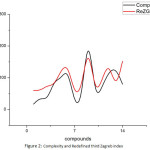Figure 2: Complexity and Redefined third Zagreb index. Click here to View figure

 

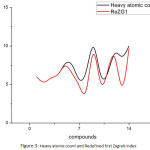Figure 3: Heavy atomic count and Redefined first Zagreb index Click here to View figure

 

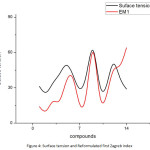Figure 4: Surface tension and Reformulated first Zagreb index Click here to View figure

 

Scope of the Work

To estimate the physiochemical properties, scientists conduct experiments which need time, space and money. Hence, thinking of an alternative to approximate these properties of compounds, graph theorists found molecular structures of the compounds called topological indices.

Conclusion

In this paper, finding the topological indices of fourteen Butane derivatives and hence plotting the graphs between physiochemical properties and topological indices made a way to see the correlation between these properties of Butane derivatives and their topological indices. We have seen that in each of the graphs the topological values are either coming very close to the physiochemical values of Butane derivatives or they are proportionate which further gives a scope of predicting the physiochemical values of Butane derivatives which is unknown from its topological index obtained from its chemical graph. This will be a great contribution to chemical world of Butane compounds. We can extend the studies to other compounds as well.

Acknowledgement

The authors would like to place on record their sincere gratitude to CHRIST (Deemed to be University) for providing the support in carrying out this project.

References

1. PubChem, [Online]. Available: http://pubchem.ncbi.nlm.nih.gov, 2018.
2. Xu, K.; Das, K. C. Discrete Appl. Math., 2011, 159, 1631-1640.
   CrossRef
3. Vijayabarathi, A.; Anjaneyulu, G. S. G. N. Int. J. ChemTech Res., 2013, 5, 1847-1853.
4. Balaban, A. T. J. Ch. Inf. Comp. Sci., 1985, 25, 334-343.
5. Zhou, B.; Stevanović, D. MATCH Commun. Math. Comput. Chem., 2006, 56, 571-578.
6. Zhou, B.; Trinajstić, N. J. Math. Ch., 2010, 48, 714-719.
   CrossRef
7. Gutman, I. Croat. Chem. Acta, 2013, 86, 351-361.
   CrossRef
8. Das, K. C.; Trinajstić, N. Comp. Math. Appl., 2011, 62, 1758-1764.
   CrossRef
9. Farahani, M. R.; Vlad, M. P. Studia UBB Chemia, 2013, 58, 133-142.
10. Zhou, B.; Du, Z. MATCH Commun. Math. Comput. Chem., 2010, 63, 181-198.
11. Kulli, V. R. Ann. Pure Appl. Math., 2017, 13, 165-172.
    CrossRef
12. Ranjini, P. S.; Lokesha, V.; Usha, A. Int. J. Graph Theory, 2013, 1, 116-121.
13. Gao, W.; Wang, W.; Farahani, M. R. J. Chem., 2016, 2016.
14. Farahani, M. R.; Gao, W. British J. Math. Comput. Sci., 2016, 13, 1-8.
    CrossRef
15. Ranjini, P. S.; Usha, A.; Lokesha, V.; Deepika, T. Asian J. Math. Comput. Res., 2016, 9, 161-166.
16. Gao, W.; Kanna, M. R. R.; Suresh, E.; Farahani, M. R. Geol. Ecol. Landscapes, 2017, 1, 173-183.
    CrossRef
17. Kumar, R. P.; Nandappa, D. S.; Kanna, M. R. R.; Bettampady, P. Int. J. Math. Anal., 2017, 11, 493-502.
    CrossRef
18. Vetrík, T. Sci. Bull. – Univ. Politeh. Bucharest, Ser. B, 2018, 80, 157-162.
19. Miličević, A.; Nikolić, S.; Trinajstić, N. Mol. Diversity, 2004, 8, 393-399.
    CrossRef
20. Su, G.; Xiong, L.; Xu, L.; Ma, B. Filomat, 2011, 25, 75-83.
    CrossRef
21. De, N. Appl. Math. Sci., 2012, 6, 5005-5012.
22. Ilić, A.; Zhou, B. Discrete Appl. Math., 2012, 160, 204-209.
    CrossRef
23. Ji, S.; Li, X.; Huo, B. MATCH Commun. Math. Comput. Chem., 2014, 72, 723-732.
24. Zhou, B.; Trinajstić, N. J. Math. Ch., 2010, 47, 210-218.
    CrossRef
25. De, N.; Nayeem, S. M. A.; Pal, A. Math., 2015, 3, 945-960.
    CrossRef
26. De, N. J. Nanosci., 2016, 2016.
27. Kulli, V. R. Int. J. Math. Arch., 2017, 8, 99-106.
28. De, N. arXiv:1704.05476v1 [cs.DM], 2017.
29. Ghalavand, A.; Ashrafi, A. R. Malaya J. Math., 2017, 5, 524–530.
30. Husin, M. N.; Hasni, R.; Imran, M. Int. J. Networking and Virtual Organ., 2017, 17, 46-63.
    CrossRef
31. Gutman, I.; Kulli, V. R.; Chaluvaraju, B.; Boregowda, H. S. J. Int. Math. Virtual Inst., 2017, 7, 53-67.
32. Pattabiraman, K.; Santhakumar, A. Caspian J. Math. Sci., 2018, 7, 25-35.
33. Kaladevi, V.; Murugesan, R.; Pattabiraman, K. Carpathian Math. Publ., 2018, 9, 134-144.
    CrossRef
34. Zhou, B.; Trinajstić, N. J. Math. Chem., 2009, 46, 1252-1270.
    CrossRef
35. Xing, R.; Zhou, B.; Trinajstić, N. J. Math. Chem., 2010, 48, 583-591.
    CrossRef
36. Wang, S.; Zhou, B.; Trinajstić, N. Filomat, 2011, 25, 29-42.
    CrossRef
37. Du, Z.; Zhou, B. Bull. Malays. Math. Sci. Soc., 2012, 35, 101-117.
38. Zhou, B.; Trinajstić, N. Croat. Chem. Acta, 2012, 85, 363-365.
    CrossRef
39. Lucic, B.; Sovic, I.; Batista, J.; Skala, K.; Plavsic, D.; Beslo, D.; Trinajstić, N. Current Computer-Aided Drug Design, 2013, 9, 184-194.
    CrossRef
40. Farahani, M. R. J. Appl. Phys. Sci. Int., 2015, 3, 99-105.
41. Kanabur, R.; Shigehalli, V. Gen. Lett. Math., 2017, 2, 150-169.
42. Kulli, V. R.; Chaluvaraju, B.; Diwakar, S. A. J. Comput. Math. Sci., 2018, 9, 117-122.
43. Babujee, J. B.; Ramakrishnan, S. Appl. Math. Sc., 2012, 6, 5383-5401.
44. Hosamani, S. M.; Perigidad, D. M.; Jamagoud, S. Y.; Maled, Y. B.; Gavade, S. J. Stat. Appl., 2017, 6, 1-11.
45. Kanna, M. R. R.; Jagadeesh, R. Int. J. Math. Appl., 2018, 6, 271–279.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.