Estimation of Lattice Constants and Band Gaps of Group-III Nitrides Using Local and Semi Local Functionals

Introduction

Group III- nitride semiconducting materials form the host material system for the fabrication of optoelectronic devices working in wide spectrum from infrared region to ultraviolet region.^1-3  Alloying the other group III or V elements in host material tune the optical and structural properties for desired potential applications. There are reports, which show the nonlinear variation in structural properties and strong shrink in band gap of InNBi alloy with composition of Bi.⁴ For both wurtzite and zinc blende phases, in band gap varies from 0.8 eV to 3.5 eV of InGaN alloys with Ga composition.⁵ For designing new materials and tailoring them for desired optical applications, we need a fast and accurate determination of their band gap values. The calculation of properties of proposed materials using computational methods provides an efficient way for the experimentalist to predict band gap prior to their synthesis. Density functional theory based methods are tools of interest to compute these properties due to their low computational cost. The standard DFT local LDA and semi local GGA exchange correlation functional suffered from self-interaction problem, which leads to the underestimation of band gaps relative to experimental values.^6-8 Therefore, alternative methods are used to predict accurate band gaps of materials. Quasi particle self-consistent GW method gives best theoretical description of electronic properties of materials.^9-11 However due to their large computational cost these methods usually not applied to large systems. The hybrid semi local exchange with nonlocal Fock exchange^12-13 provides the band gaps comparable to GW results at a relatively low cost still much expensive as compared to standard local and semi local exchange functional. Recently Tran and Blaha proposed a multiplicative exchange potential¹⁵ modifying over original Becke Johnson potential¹⁵ which predict the band gap with accuracy comparable to GW method but at cost in the range of semi local functional. We used the TB-mBJ potential to calculate theoretical band gaps of Group III nitrides in wurtzite and Zinc blende structures using original and improved parameterization for empirical parameter ‘c’ in equation (4) of reference.¹⁶

A small deviation in lattice parameters may result in significant variation in band gaps for same semiconductor.¹⁷ Therefore, while calculating band gap the optimization of lattice parameters should be done in an efficient way, which in turn depends upon the selection of proper exchange correlation functional. TB-mBJ is an exchange potential and cannot be obtained as a derivative of exchange correlation energy. Thus, lattice parameters have to be optimizing with LDA or GGA approximation before calculating the band structure with TB-mBJ potential.¹⁴ Kohn Sham (KS) equations based density functional theory^18,19 the exact exchange correlation functional is not known. Thus, it is of utmost importance to select a proper functional for the problem in hand.

In the present work, we performed the optimization of lattice parameters of materials under study of group-III nitrides using four approximations i.e. LDA,^20,21 PBE,^{22, 23} WC²⁴ and PBEsol.²⁵ With these lattice parameters, the band gaps were calculated using mBJLDA exchange correlation potential with original and improved version suggested for semiconductors having band gap below 7 eV.

Method

All the calculations were carried out using DFT based all electron full potential linearized augmented plane wave and local orbital (FPLAPW + lo) method as implemented in wein2k code.²⁶ Three GGA functionals i.e. PBE, WC and PBEsol were considered for taking into account the exchange correlation effect. For improving the band gaps as obtained with local and semilocal functional, we employed mBJ exchange potential in combination with LDA correlation.¹⁴ The mBJ exchange potential is defined by equation (4) of reference.¹⁶

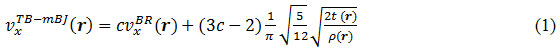
Where ρ being the electron density, t is the kinetic energy density and

is the Becke-Russel potential and parameter c is given by

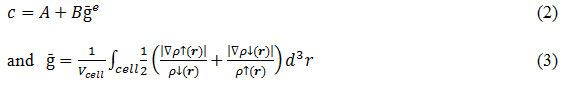
In equation (2) A, B and e are the parameters whose values are fitted according to the experimental values. The parameters suggested in original and improved form of mBJ approximation are shown in Table 1.

Table 1: The values of parameters A, B and e used for calculations of ‘c’ in [Eq. (2)].

	A	B	e
Poriginal	-0012	1.023	0.5
Psemiconctor	0.267	0.656	1

 

In table 1, P_original and P_{semiconductor}  are the parameterization used for calculation of ‘c’ in original and improved form of mBJ approximations as suggested by Tran & Blaha¹⁴ and D. Koller respectively.¹⁶ All the calculations were converged with respect to number of  k- points in Brillouin zone and the value of R_mt K_max (between 8 and 10)  defining the size of basis set used. For analyzing results, the following statistical quantities have been used: mean error (ME), mean absolute error (MAE), mean relative error (MRE, in percentage), and mean absolute relative error (MARE, in percentage).

Results and Discussion
Equilibrium Lattice Constant
At ambient conditions III-nitride semiconductors prefer to crystallize in hexagonal structure with space group P6₃mc.²⁷ However, these materials can also be grown in zinc blende structure using experimental techniques like molecular beam epitaxy.²⁷ The wurtzite structure can be supposed to be the interpenetration of the two hexagonal structures with relative displacement along c axis of unit cell while zinc blende structure can be imagined as the interpenetration of two face centered cubic structures with one displaced relative to other by one fourth along body diagonal of unit cell. The wurtzite structure is characterized by three parameters namely a, c/a and u while the zinc blende unit cell by only one parameter a.

Table 2: Equilibrium lattice parameters (in Å) of III-N semiconductors, calculated with LDA, PBE, WC and PBEsol along with Experimental values.²⁸

Material		LDA	PBE	WC	PBEsol	Expt.
wzInN	a	3.5073	3.5852	3.5421	3.5408	3.545
	c	5.6689	5.7916	5.7226	5.7191	5.703
zbInN	a	4.9461	5.0545	4.9942	4.9921	4.98
wzAlN	a	3.0908	3.132	3.1142	3.1151	3.112
	c	4.9478	5.0219	4.9874	4.987	4.982
zbAlN	a	4.3467	4.4064	4.38	4.3809	4.38
wzGaN	a	3.1593	3.2219	3.1893	3.1884	3.189
	c	5.1497	5.248	5.1964	5.1939	5.185
zbGaN	a	4.4619	4.5512	4.5073	4.5058	4.5
	ME	-0.0341	0.048	0.00639	0.00513
	MAE	0.0341	0.048	0.00703	0.0063
	MRE(%)	-0.799	1.069	0.124	0.101
	MARE(%)	0.799	1.069	0.142	0.131

 

The optimized lattice parameters obtained with different approximations are shown in table 2 with respective errors ME, MAE, MRE and MARE in various calculations written at bottom of the table. The calculated results are also shown graphically in fig 1 in which the inclined straight line represents the experimental values while calculated parameters by different symbols.

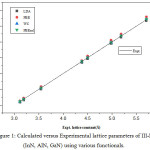Figure 1: Calculated versus Experimental lattice parameters of III-N (InN, AlN, GaN) using various functionals. Click here to View figure

 

The graph shows that the PBEsol lattice constants lie closest to experimental values as compared to other results. The equilibrium LDA lattice constant underestimate while PBE overestimate the experimental values with ME of -0.0341 Å and 0.048 Å respectively as reported earlier.²⁹ The functional WC and PBEsol yields the lattice constants much closer to experimental values as suggested by lowest values of statistical quantities written at the bottom. With small differences in ME, MAE, MRE and MARE for WC and PBEsol approximations, both of these functional are equally applicable for optimization of lattice constant for Group-III nitrides. Table 3 shows a comparison of our calculated WC and PBEsol optimized lattice constants with hybrid density functional results^30,31 and lattice parameters optimized with OPT functional as given in recently proposed database.³² The comparison concludes that PBEsol reproduces the experimental values in better way, supported by minimum values of ME and MAE of 0.0063 Å and 0.0073 Å when compared with present WC, hybrid functional used in reference³¹ with ME, MAE of -0.0073 Å, 0.0091 Å and OPT functional used in reference³² with ME and MAE of 0.041 for InN, AlN, GaN in wurtzite and zinc blende structures respectively. The hybrid functional with optimized α parameter used in reference³⁰ underestimate the lattice constants for III-N semiconductors in zinc blende phase with ME of -0.018 Å while  the present PBEsol results overestimate with ME of 0.0063Å.

Table 3: Comparison of WC and PBEsol optimized lattice constants (Å) with hybrid and OPT functional results.

		WC	PBEsol	Hybrid	OptB88-vdWc	Expt.
wzInN	a	3.5421	3.5408	3.542b	3.572	3.545
	c	5.7226	5.7191	5.711b	5.784	5.703
zbInN	a	4.9942	4.9921	4.956a, 4.988b	5.039	4.98
wzAlN	a	3.1142	3.1151	3.103b, 3.064d	3.13	3.112
	c	4.9874	4.987	4.970b,4.908d	5.021	4.982
zbAlN	a	4.38	4.3809	4.367a,4.363b	4.404	4.38
wzGaN	a	3.1893	3.1884	3.180b,3.232d	3.211	3.189
	c	5.1964	5.1939	5.172b,5.268d	5.24	5.185
zbGaN	a	4.5073	4.5058	4.483a,4.489b	4.541	4.5

 

All the experimental values are taken from ref. 28.

^a from ref. 30.

^b from ref. 31.

^c from ref. 32.

^d from ref. 33.

Band gap

The calculated band gap values for III-nitrides in wurtzite and zinc blende structures are shown in table 4 along with the various errors namely ME, MAE, MRE, MARE given at bottom of the table. The results are also shown graphically in figure 2. All the local and semilocal functionals strongly underestimate the band gaps with mean error of about – 1.5 eV mean relative error of about -60%. This is due to self interaction effect suffered by the respective functional used. The application of mBJ exchange potential in association with LDA correlation as suggested by Tran Blaha¹⁴ improves the band gaps leading to a decrease in ME and MARE to values of order of -0.2eV and 10% respectively. A further slight improvement in band gap is obtained with improved version¹⁶ of mBJLDA approximation leading to the reduction in various errors as shown at the bottom of the table 4 except for the results at LDA optimized lattice constants where the errors increase. Further, in case of wz InN the improved mBJLDA approximation increases the deviation from experimental values as compared to original mBJLDA version. The best agreement with experimental values is obtained with mBJLDA approximation at LDA optimized parameters with MAE and MARE of 0.162eV and 7.41% respectively. However the results obtained with improved  mBJLDA at WC and  PBEsol  optimized lattice constants also compete in accuracy with mBJLDA + LDA as suggested by MAE and MARE values of 0.198eV, 0.199eV  and 9.81%, 9.99% respectively.

Table 4: Calcalated band gap (eV) with local, semilocal functional, original mBJLDA and improved mBJLDA (mBJLDASC) for semiconductors. Experimental values are taken from reference.²⁸

	LDA	mBJLDA	mBJLDA(SC)	PBE	mBJLDA	mBJLDA(SC)	WC	mBJLDA	mBJLDA(SC)	PBEsol	mBJLDA	mBJLDA(SC)	Expt.
wzInN	0	0.978	1.169	0	0.739	0.913	0	0.866	1.05	0	0.87	1.052	0.78
zbInN	0	0.758	0.939	0	0.535	0.696	0	0.657	0.827	0	0.67	0.839	0.78
wzAlN	4.397	5.759	5.926	4.029	5.391	5.544	4.104	5.55	5.715	4.096	5.546	5.705	6.19
zbAlN	3.242	4.913	5.104	3.311	4.846	5.016	3.22	4.871	5.05	3.188	4.851	5.03	4.9
wzGaN	2.089	3.337	3.566	1.707	2.954	3.171	1.825	3.152	3.376	1.857	3.162	3.386	3.503
zbGaN	1.93	3.148	3.36	1.546	2.768	2.975	1.654	2.952	3.163	1.682	2.959	3.168	3.29
ME	-1.297	0.092	0.104	-1.475	-0.368	-0.188	-1.44	0.232	-0.0437	1.437	-0.231	0.0438
MAE	1.297	0.162	0.192	1.475	0.368	0.271	1.44	0.261	0.199	1.437	0.261	0.198
MRE (%)	-57.42	-7.33	12.33	-61.94	-13.7	-3.47	-60.94	-5.99	4.76	-60.77	-0.925	6.15
MARE (%)	57.42	7.41	13.75	61.94	13.7	9.95	60.94	9.67	9.81	60.77	9.47	9.997

 

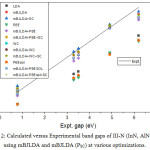Figure 2: Calculated versus Experimental band gaps of III-N (InN, AlN, GaN) using mBJLDA and mBJLDA (PSC) at various optimizations. Click here to View figure

 

On comparing our results with other mBJLDA band gaps we found an improvement as shown in table 5, this is due to the reason that the reported calculations were performed at experimental lattice constants while our calculations are at optimized parameters which is obvious as suggested by J.A. Camargo that the band gaps calculated with experimental lattice constants show greater deviation from experimental band gap values using mBJLDA potential.¹⁴

Table 5: Comparison of band gap (eV) with other reported results.

	mBJLDA	mBJLDA SC+PBEsol	mBJLDA34	HSEα30	B3PW9135	GW36	mBJLDA+OPT32	Expt.
wzInN	0.978	1.052	0.89		0.85	0.61	0.76	0.78
zbInN	0.758	0.839		0.674		0.38	0.58	0.78
wzAlN	5.759	5.705	5.51		6.05	6.40	5.2	6.19
zbAlN	4.913	5.03	4.88	5.383	4.94	5.19	4.8	4.9
wzGaN	3.337	3.386	3.17		3.44	3.45	3.084	3.503
zbGaN	3.148	3.168	2.85	3.312	3.08	3.30	2.9	3.29

 

As GW and hybrid density functional methods are known for the best theoretical methods to describe the electronic structure of solids so it is necessary to compare our results with above said methods, in addition, the band gaps calculated at OPT optimized lattice parameters as given in recently launched database³² are also shown in table 5 for comparison. The MAE of 0.198eV for mBJLDA band gaps suggest that this approximation have the  accuracy of the order of hybrid density functional and GW methods having the MAE of  0.105 eV and 0.189 eV respectively as implemented in references³⁵ and³⁶ respectively   but at relatively lower computational cost. For zinc blende III-N semiconductors, mBJLDA with PBEsol optimized geometry gives band gaps in better agreement with experimental values with MAE of 0.104 eV as compared to 0.203 eV when calculated with hybrid density functional method as reported in reference³⁰ by Bastos et. al. The band gaps of III-N semiconductors, reported in JARVIS-DFT database calculated with mBJ exchange potential at optB88vdW functional (OPT) are found to underestimate the experimental gaps with ME, MAE, MRE and MARE -0.353eV, 0.353eV,   -11.65%, 11.65%  respectively.³² While our calculated mBJLDA band gaps at PBEsol optimized lattice parameters predict the band gaps with respective values of statistical quantities as 0.0438eV, 0.198eV, 6.15%, 10%.

Conclusions

We have made a systematic investigation, by the use of various local and semi local functionals, for optimization of lattice constants and prediction of band gaps of group-III nitrides (InN, AlN, GaN) in wurtzite and zinc blende structures. Importantly, the  PBEsol exchange correlation functional is found to provide lattice constant closest to experimental values shown by smallest M(A)E, M(A)RE of 0.00513 Å (0.0063 Å) and 0.101% (0.131%) with WC approximation also competing it with corresponding errors 0.00639 Å (0.00703 Å) and 0.124% (0.142%) for the materials studied. Further, these approximations have also predicted the band gap values closer to their experimental values when combined with mBJLDA potential with parameterization suggested for semiconductors. However, the best agreement for band gap values with experiment is obtained with mBJLDA +LDA approximation.

Acknowledgement

The authors thank Fabien Tran for valuable discussion through wien2k official mailing list.

References

1. Jani, O.; Ferguson, I.; Honsberg, C. & Kurtz, S. Appl. Phys. Lett. 2007 91, 132117.
   CrossRef
2. Dahal, R., Pantha, B., Li, J., Lin, J. & Jiang, H. Appl.Phys. Lett. 2009 94, 063505.
   CrossRef
3. Nakamura, S. & Fasol, G. Springer 1997 (ed. Nakamura, S. & Fasol, G.)50.
4. Lu ,P.; Liang,D.; Chen,Y.; Zhang, C.; Quhe, R.; Wang S. Scientific Reports 2008, Article number : 10594.
5. Gan, C. K.; Feng, Y. P.; Srolovitz D. J. Phys. Rev. B. 2006, 73, 235214.
   CrossRef
6. Perdew, J. P.; Zunger, A.; Phys. Rev. B 1981, 23, 5048.
   CrossRef
7. Perdew, J..P.; Levy, M.; Phys. Rev. Lett. 1983, 51, 1884.
   CrossRef
8. Jones, R.O.; Gunnarsson, O. Rev. Mod. Phys. 1989, 61, 689.
   CrossRef
9. Hedin, L. Phys. Rev. 1965, 139, A796.
   CrossRef
10. Hybersten, M. S.; Louie, S. G. Phys. Rev. B : Condens. Matter Mater. Phys. 1986, 34, 5390.
11. Shishkin, M. S.; Marsman, M.; Kreese, G. Phys. Rev. Lett. 2007, 99, 246403.
    CrossRef
12. Perdew, J. P.; Erhzerhof, Burke, K. J. Chem. Phys. 1996, 105, 9982.
    CrossRef
13. Adamo, C.; Barone, V. J. Chem. Phys. 1999, 110, 6158.
    CrossRef
14. Tran, F.; Blaha, P. Phys. Rev. Lett. 2009, 102, 226401.
    CrossRef
15. Becke, A. D.; Johnson, E. R. J. Chem. Phys. 2006 124, 221101.
    CrossRef
16. Koller. D.; Tran, F.; Blaha, P. Phys. Rev. B 2012, 85, 155109.
    CrossRef
17. Camargo, J. A.; Martinez, Baquero, R. Phys. Rev. B 2012, 86, 195106.
18. Hohnberg, P.; Kohn, W. Phys. Rev. 1964, 136, B864.
    CrossRef
19. Kohn, W.; Sham, L.J. Phys. Rev. 1965, 140, A1133.
    CrossRef
20. Dirac, P. A. M.  Proc. Camb. Philos. Soc. 1930, 26, 376.
    CrossRef
21. Perdew, J. P.; Wang, Y. Phys. Rev. B  1992, 45, 13244.
    CrossRef
22. Perdew, J. P.; Chevary, J. A.; Vosko, S. H.; Jackson, K.A.; Pederson, M. R.; Singh, D. J.; Fiolhais, C. Phys. Rev. B 1992, 46, 6671.
    CrossRef
23. Perdew, J. P.; Burke, K.; Ernzerhof, M. Phys, Rev. Lett. 1996, 77, 3865.
    CrossRef
24. Wu, Z.; Cohen, R. E. Phys. Rev. B 2006, 73, 235116.
    CrossRef
25. Perdew, J. P.; Ruzsinszky, A.; Csonka, G. I.; Vydrov, O. A.; Scuseria, G. E.; Constantin, L.A.; Zhou, X.; Burke, K. Phys. Rev. Lett. 2008, 100, 136406.
    CrossRef
26. Blaha, P.; Schwarz, K.; Madsen, G. K. H.; Kvasnicka, D.; Lnitz, J. Vienna University of Technology, Austria, 2001.
27. Morkoc, H. Handbook of Nitride Semiconductors and Devices, 2008, Vol.1, WILEX-VCH Verleg, GmbH & Co. KGaA, Weinhein.
28. Vurgaftman, I.; Meyer, J. R. J. Appl. Phys. 2003, 94, 3675.
    CrossRef
29. Hass, P.; Tran, F.; Blaha, P. Phys. Rev. B 2009, 79, 085104.
    CrossRef
30. Bastos, C. M. O.; Sabino, F. P.; Sipehi, G. M.; Da Silva, L. F. J. Appl. Phys. 2018, 123, 065702.
    CrossRef
31. Caro, M. A.; Schulz, S.; O’Reilly, E. P. Phys. Rev. B 2012, 86, 014117.
    CrossRef
32. Choudhary, K.; Zhang, Q.; Reid, A. C. E.; Chowdhary, S.; Nguyan, N. V.; Trautt, Z.; Newrock, M. W.; Congo, F. X.; Tavazza, F. Scientific Data 2018, Article no. 05.
33. Qin, L.; Duan, Y.; Shi, H,; Shi, l.; Tang, G. J. Phys. : Condens. Matter 2013, 25, 045801.
    CrossRef
34. Tran, F.; Blaha, P. J. Phys. Chem. 2017, A121, 3318.
    CrossRef
35. Crowley, J. M.; Tahir Kheli, J.; Goddard, W. A. J. Phys. Chem. Lett. 2016, 7, 1198.
    CrossRef
    
36. Deguchi, D.; Sato, K.; Kino, H.; Kotani, T. Jpn. J. Appl. Phys. 2016, 55, 051201.
    CrossRef

---

This work is licensed under a Creative Commons Attribution 4.0 International License.