Vibrational Analysis and Non Linear Optical Activity of 3-fluoro-4–methylbenzonitrile

Introduction

Benzonitrile is an aromatic organic compound. Derivatives of benzonitrile find application in industries and medical field (M. Alcolea Palafox, 2003). Benzonitrile compounds are used as preservatives for food products. They are used for making aniline blue a dye. In medical field many benzonitrile derivatives in solid form are used as urinary antiseptic and vapour form are used for disinfecting bronchial tubes (Hermann Imgartinger, 2000). Since the derivatives of benzonitrile have wide applications,many studies are reported on such compounds. First order hyperpolarizability and HOMO-LUMO energy are the most important tools to predict the NLO activity of a compound. Quantum chemistry calculations provides the entire information about the structural, vibrational, electronic, optical, thermodynamic and other related properties of a molecule (David Pegu, 2013). Hence the present analysis was carried out to study the molecular properties of 3-fluoro- 4 – methylbenzonitrile and to elucidate useful information about the molecule.

Experimental Details

The compound 3-Fluoro-4-methylbenzonitrile (3F4MBN) was purchased from sigma-Aldrich Chemical Company, USA with a purity of not less than 99% and used as such for experimental studies. FT-Raman spectra of 3F4MBN  was inscribed using 1064 nm line of Nd:YAG laser as the exciting wavelength in range 50-3500 cm^-1 on a EZRaman, Enwaveoptronics, USA IFS 66 V spectrometer. Fourier transform infrared (FTIR) spectra was inscribed using 8400S Bruker, AlphaT,Germany infrared spectrophotometer using KBr pellet technique in the range 4000–400 cm^-1. The spectra has been inscribed at normal temperature with a scanning speed  30 cm^-1 min^-1.

Computational Details

All calculations has been met with Gaussian 09 program package [M.J. Frisch, 2009] with  the aid of DFT with B3LYP using 6-311++G(d,p) basis set and  results were viewed using GAUSS VIEW program. HOMO and LUMO energy was obtained from time dependent density functional theory. NBO analysis has been executed using  same basis set to study molecular interaction between filled and vacant orbitals. Polarizability and hyperpolarizability were also calculated.

Table 1: Geometrical Parameters of 3–fluoro- 4-methylbenzonitrile

Parameter	B3LYP	Parameter	B3LYP	Parameter	B3LYP
BondLength(Å)	6-311G++(d,p)	Bond Angle(°)	6-311G++(d,p)	Dihedral angle	6-311G++(d,p)
C1-C2	1.554	C2-C1-H11	109.5741	H11-C1-C2-C3	-150.8946
C1-H11	1.0675	C2-C1-H12	108.9205	H11-C1-C2-C7	29.386
C1-H12	1.072	C2-C1-H13	109.8545	H12-C1-C2-C3	89.2887
C1-H13	1.0814	H11-C1-H12	109.5449	H12-C1-C2-C7	-90.4308
C2-C3	1.3571	H11-C1-H13	109.3711	H13-C1-C2-C3	-30.7176
C2-C7	1.5456	H12-C1-H13	109.562	H13-C1-C2-C7	149.563
C3-C4	1.5425	C1-C2-C3	120.0591	C1-C2-C3-C4	-178.7972
C3-H14	1.0713	C1-C2-C7	119.9809	C1-C2-C3-H14	1.1997
C4-C5	1.3563	C3-C2-C7	119.9594	C7-C2-C3-C4	0.9223
C4-H15	1.0712	C2-C3-C4	119.8227	C7-C2-C3-H14	-179.0808
C5-C6	1.5359	C2-C3-H14	120.3491	C1-C2-C7-C6	177.7006
C5-C9	1.5345	C4-C3-H14	119.8282	C1-C2-C7-C8	-2.5711
C6-C7	1.362	C3-C4-C5	120.2109	C3-C2-C7-C6	-2.0191
C6-H16	1.0687	C3-C4-H15	119.6262	C3-C2-C7-C8	177.7092
C7-F8	1.3528	C5-C4-H15	120.1614	C2-C3-C4-C5	1.422
C9-N10	1.1563	C4-C5-C6	120.064	C2-C3-C4-H15	-179.0196
		C4-C5-C9	119.8784	H14-C3-C4-C5	-178.5748
		C6-C5-C9	120.0563	H14-C3-C4-H15	0.9835
		C5-C6-C7	119.9799	C3-C4-C5-C6	-2.6347
		C5-C6-H16	119.9932	C3-C4-C5-C9	176.9544
		C7-C6-H16	120.0269	H15-C4-C5-C6	177.8093
		C2-C7-C6	119.9001	H15-C4-C5-C9	-2.6016
		C2-C7-F8	120.2341	C4-C5-C6-C7	1.5281
		C6-C7-C8	119.8652	C4-C5-C6-H16	-178.4505
				C9-C5-C6-C7	-178.0602
				C9-C5-C6-H16	1.9612
				C5-C6-C7-C2	0.8132
				C5-C6-C7-C8	-178.9161
				H16-C6-C7-C2	-179.2082

 

Results and Discussion

Geometric Structure

The optimized geometrical structure of 3-fluoro- 4 – methylbenzonitrile is shown in Fig.1. The optimized bond length, bond angle and dihedral angle are calculated using B3LYP 6-311++G(d,p) basis set. The geometrical parameters calculated are shown in Table 1. These parameters can be utilized to elucidate other  parameters of the compound under investigation.

Figure 1: Optimized geometry of 3-fluoro- 4-methylbenzonitrile   Click here to View figure

 

Vibrational Analysis

The investigated compound has 16 atoms and so it possess 42 normal modes of vibrations. Vibrational frequencies calculated and observed are shown in table 2.

C-H vibrations

C-H stretching vibrations in aromatic compounds appear in the range 3100-3000 cm^-1(M. Silverstein, 1989). In this study the peak at 3078 cm^-1 and  3068 cm^-1 in the FTIR spectrum and FT-Raman Spectra respectively are ascribed to C-H stretching vibrations. The corresponding calculated values are 3086 cm^-1and 3060 cm^-1which are in accordance with the observed values. For substituted benzenes, the three in-plane C-H vibrations appear in a range 1300-1000 cm^-1and three out-of-plane bending vibrations appear in a range 1000-750 cm^-1(J. Sharmi Kumar, 2015). The peaks at 1142, 1194, 1214 ,  1252 cm^-1 and at 1132, 1200 cm^-1 in the FTIR spectrum and FT-Raman Spectrum are ascribed to in-plane C-H bending  vibrations which are in accordance with the calculated values 1130, 1171, 1216 and 1276 cm^-1 . The peaks at 831, 886 and 951 cm^-1 and at 867, 936 cm^-1 in the FTIR spectrum in the FT-Raman Spectrum are ascribed to out- of -plane C-H bending  vibrations which are in accordance with the calculated values 836, 896 and 950 cm^-1.

C-C vibrations:  Ring C-C stretching vibration appears in a range 1650-1400 cm^-1(N. Sundaraganasan, 2009). Peaks at 1492 cm^-1, 1562 cm^-1 and at 1494 cm^-1, 1591 cm^-1 in the FTIR spectrum and FT-Raman Spectrum are ascribed to C-C vibrations. The corresponding worked out values are 1494 cm^-1 , 1564 cm^-1 and 1492 cm^-1 ,1531 cm^-1 which are in accordance with the observed data.

C-F vibrations: C-F vibration appears in the range 1360-1000 cm^-1 (K. Sambathkumar, 2015). The sharp peak at 1270 cm^-1 and at 1285 cm^-1 in the FTIR spectrum and FT-Raman Spectra are ascribed to C-F vibrations and are in accordance with  calculated values 1270 cm^-1and 1276 cm^-1.

Vibrations:  vibration appears around 2200 cm^-1 (S.Gunasekaran, 2006). The peak at 2244 cm^-1 and at 2221 cm^-1 in the FTIR spectrum and FT-Raman Spectra are ascribed to  vibrations which are in accordance with  calculated values 2242 cm^-1and 2238 cm^-1.

CH₃group vibrations: The title compound has only one substituted methyl (CH₃) group in the fourth position of the benzene ring. A methyl group is associated with nine fundamental mode of vibrations namely , the symmetric stretching mode (CH₃ sym. stretch) , asymmetric stretching  mode (CH₃ asym. stretch), in-plane hydrogen stretching mode,  the symmetric deformation mode(CH₃ sym. deform) , asymmetric deformation mode(CH₃ asy. deform),  the in-plane rocking mode (CH₃ ipr), out-of-plane rocking mode (CH₃ opr) and twisting (tCH₃) mode. Substituted methyl groups in the aromatic ring systems are typically specified as electron donating groups (D. Lin-Vein, 1991).

Generally CH₃ vibration appear in a range (2900-3000 cm^-1)(M. Murugan, 2012). Peak at 3000 cm^-1 and at 2986 cm^-1 in the FTIR spectrum and FT-Raman Spectra are ascribed to CH₃ symmetrical stretching mode vibration which are in accordance with the calculated value 3035cm^-1. The peak at 1499cm^-1 in the FTIR spectrum corresponds to CH₃ in plane bending modes which is in accordance with the calculated value 1492cm^-1. The peak at 1069cm^-1 in the FTIR spectra harmonize to CH₃ in rocking mode vibration which is in accordance with the calculated value 1060cm^-1.

Table 2: Observed and calculated (FT-IR, FT-Raman) vibrational frequencies of the title compound.

Mode	Label	Experimental(cm-1)FT-IR	FT-Raman	B3LYP/6-311++G(d,p)	IR Intensity(Km/mol)	Raman Activity	Vibrational assignments
1	A			95.7103	0.0009	0.3696	τCH3
2	A			104.1663	1.438	0.4454	τC≡N
3	A		154	148.0831	5.0946	3.2263	βC≡N
4	A		194	197.8587	3.2846	1.3948	γC-CH3+γC≡N
5	A		273.7	276.2751	2.2767	0.3873	βC-CH3+βC-F
6	A		280	282.9399	2.3928	0.6734	ω C-F
7	A		414	409.8928	1.4935	4.0477	γC-CH3
8	A		423	432.2994	1.4908	3.9706	16a γ C-C-C
9	A		434	436.6913	1.945	1.5209	β C-C-C
10	A	513.3	462.6	491.5191	2.5994	1.6762	16b γ C-C-C
11	A	560.4	544	545.9524	3.7765	7.3407	16b β C-C-C
12	A	611.8	615.8	603.8151	2.6259	0.9818	16a β C-C-C
13	A	632.4	620	643.1389	10.0649	1.2955	6a δ
14	A		685.8	700.6038	0.7185	2.4935	γ C-C-C+t C≡N
15	A	753.2	754	713.601	1.7294	0.3961	γ C-C-C+t C≡N
16	A	768.3		769.1046	5.0664	24.505	β C-C-C+t C-F
17	A	831.4		836.704	23.2161	0.1268	17b γ C-H
18	A	886.4	867	896.4401	24.4011	0.1313	γ C-H+τ C≡N
19	A	951.45	936	950.8395	21.1946	4.5349	10a γ C-H
20	A	993.8		970.5941	0.0134	0.0512	Ring breathing
21	A	1007.4	1006	1019.558	18.0624	0.9225	Trigonal bending
22	A	1069		1060.461	2.6859	0.0411	ρ CH3
23	A	1142.5	1132	1130.859	36.0379	19.7862	β CH+ υ C-F
24	A	1194.9		1171.555	0.575	3.0025	β CH
25	A	1214.5	1200	1216.88	3.7437	1.9298	β CH+ υ C-F
26	A	1270.4	1277	1276.279	78.5627	76.1255	β CH
27	A		1285	1295.275	1.0495	1.5283	υ C-F
28	A		1332	1329.431	0.409	2.3016	γC-CH3
29	A	1429.5	1410	1419.072	3.2555	20.0889	CH3 asym.deform
30	A	1469.5		1439.191	29.835	0.7039	CH3 asym.deform
31	A	1472	1487	1480.588	8.2457	9.5451	14 υ C-C
32	A	1499		1492.38	8.7334	13.1925	β CH3
33	A	1572.6	1584.7	1531.799	50.2532	1.5091	19a υ C-C
34	A	1600		1601.005	40.2309	2.2114	8b  υ C-C (semi-circle stretch)
35	A	1668.6	1658	1656.248	2.154	172.8537	8a  υ C-C
36	A	2338	2338	2333.982	43.5827	557.747	γ C≡N
37	A	3000	2986	3035.594	15.3871	306.9231	υsym CH3
38	A	3078	3053	3086.357	8.4141	99.1312	20a** arom. υ C-H
39	A	3117	3108	3118.279	12.3515	65.7333	υ  C-H
40	A	3178		3177.419	5.5481	75.475	υ  C-H
41	A	3203	3207	3203.313	1.539	102.9211	υ  C-H
42	A	3221		3212.26	0.7115	88.4629	υ  C-H

 

υ-stretching; υ_sym-symmetrical stretching; υ_asy– asymmetrical stretching; β-in plane bending; γ-out-of-plane bending; ω-wagging; t-twisting; δ-scissoring; τ-torsion;ρ-rocking;  *-wilson’s notion; IR int-IR intensities.

Mulliken Atomic Charges

The scope of bonding of a molecule depend on the number of unpaired electrons in the atoms and hence the atomic charges has been retrieved by Mulliken population assay (A.A. Popov, 2004). Mulliken atomic Charges calculation plays an important part in applying quantum chemistry calculation to molecular systems because atomic charge affects dipole moments, polarizability, electronic structures and other properties of molecular systems (R.S.Mulliken, 1985). Mulliken charges obtained using B3LYP 6-311++G (d,p) are shown in Table 3. Mulliken atomic charges graph is shown in Fig.2. All  hydrogen atoms exhibits positive charge,  nitrogen and fluorine atom exhibit negative charge .This suggests the creation of intermolecular interaction in solid forms(Isa Sidir, 2010).From the charge calculation it is clear that nitrogen atom having negative charge acts as donor atom and the ring hydrogen atom having positive charge acts as acceptor atoms.

Table 3: MullikenPopulationAnalysis of 3–fluoro- 4-methylbenzonitrile

Sl.No	Atoms	B3LYP
1	C	-0.38354
2	C	1.303938
3	C	-0.85876
4	C	-0.53413
5	C	2.179886
6	C	-0.15444
7	C	-0.68165
8	F	-0.17206
9	C	-1.58496
10	N	-0.1711
11	H	0.178828
12	H	0.17881
13	H	0.157086
14	H	0.143043
15	H	0.190491
16	H	0.208561

 

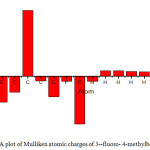Figure 2: A plot of Mulliken atomic charges of 3–fluoro- 4-methylbenzonitrile Click here to View figure

 

Polarizability and Hyperpolarizability

The reaction of  systems in  applied electric fields has been explained by its  Polarizability and hyperpolarizability. The non linear optical property of a compound can be studied using these parameters. The investigated first order hyperpolarizability of  investigated compound is 2.768×10^-30 esu which is 9 times urea (0.2991×10^-30esu) a standard NLO material (Li Xiao-Hong,2011). Calculated dipole moment, polarizability and hyperpolarizability are given in Table 4.

Table 4: Electric dipole moment, polarizability and hyperpolarizability of 3–fluoro- 4-methylbenzonitrile.

Parameters	B3LYP
	6-311++G(d,p)
μ x	0.5802156
μ y	0.010185
μ z	-1.7797845
μ=	1.87200Debye
α xx	92.0760016
α xy	-0.0391977
α yy	54.1494
α xz	0.300154
α yz	-0.5182233
α zz	145.5895464
α0	194.7552×10-33esu
α=	1682.549×10-33esu
β xxx	103.2968388
β xxy	-7.7277807
β xyy	34.3821757
β yyy	6.763047
β xxz	24.3731807
β xyz	0.135037
β yyz	-18.6541887
β xzz	28.6181066
β yzz	5.1407
β zzz	268.1870903
β0	2768.5784×10-33esu

 

HOMO LUMO Analysis

HOMO stands for highest occupied molecular orbital which represents the ability of a molecule to donate an electron and LUMO stands for lowest unoccupied molecular orbital which represents the ability of a molecule to accept an electron.  HOMO and LUMO are the major orbitals that take part in the chemical stability of the molecule (J.A. Alanso,2004). The calculated HOMO LUMO gap using B3LYP 6-311++G(d,p) is 5.61eV.  The  HOMO LUMO  energy gap explain that the title compound is experiencing charge transfer interactions and it reflects its NLO property (Basak Kosar,2011). The calculated energy values are shown in Table 5.

Table 5: Calculated energies of 3–fluoro- 4-methylbenzonitrile.

LUMO	-1.79
HOMO	-7.4
Energy Gap	5.61
Electronegativity (χ)	-4.595
Chemical Potential (µ)	4.595
Global Hardness (ƞ)	2.805
Global softness (s)	0.356506239
Electrophilicity Index (ω)	6.4444875
EHOMO-1(eV)	-7.82
ELUMO+1(eV)	-1.36
EHOMO-1 – ELUMO+1(eV)	-6.46

 

Thermodynamic Parameters

Several thermodynamical parameters has been calculated and are listed in Table 6. Scale factors were recommended (Zeynep Demircioglu, 2014) for calculating  zero point vibrational energy and entropy accurately. Changes in total energy and entropy at normal temperature are presented in Table.6.  These changes seems to be insignificant.

Table 6: Thermodynamic parameters

Thermodynamic functions Of DMAP	B3LYP
	6-311++G(d,p)
Self-consistent field energy (a.u)	-463.132
Zero point vibrational energy (kcal/mol)	74.043
Rotational constant (GHz)	3.021
	0.880
	0.684
Rotational temperature (K)	0.145
	0.042
	0.033
Thermal energy (kcal/mol)
Total	79.491
Translational	0.889
Rotational	0.889
Vibrational	77.714
Specific heat capacity at constant volume (cal/mol K)
Total	32.233
Translational	2.981
Rotational	2.981
Vibrational	26.271
Dipole moment (Debye)	4.7644
Lumo(eV)	-1.79
Homo(eV)	-7.4
Energy gap(eV)	-5.61
Entropy(S)(cal/mol K)
Total	91.514
Translational	40.614
Rotational	29.559
Vibrational	21.342
Gibbs Free Energy	0.084
Enthalpy	0.128

 

Non Linear Optical Activity

NLO activity give key function for properties like the  frequency shifting, optical modulation, optical swaping , optical logic for the extending technology in the field of communications, signal processings and optical inter-connections(Mauricio Alcolea Palafox, 2000).Molecules that exhibit asymmetric polarization which is induced because of electron donars and acceptors in the pi-electron conjugatedsystems are efficient materials for electro-optics and NLO applications (I.Khan, 2013). In order to find the non linear activity of the material, first order hyperpolarizability of the investigated compound was calculated and compared with urea, a standard NLO material. It was found that the first order hyperpolarizability of our investigated compound is 9 times  than urea.   Hence we propose that the investigated compound under study is an efficient material for  future NLO applications.

Conclusion

Detailed investigation of the structural and electronic property of the compound under study has been performed by DFT using suitable basis set. Calculated first order hyperpolarizability and HOMO- LUMO energy gap confirmed the NLO property of the compound.  First order hyperpolarizability calculated for the compound is 9 times greater than urea. Hence the compound under study is an efficient material for future NLO applications. Mulliken atomic charge calculation suggests that there is charge transfer from N, F to H.

References

1. M. Alcolea Palafox, V. K. Rastogi, L. Mittal, “Benzonitriles: Survey of their importance and scaling of their vibrational frequencies,” Int.J.Quantum Chem., vol. 94, pp 189-204, January 2003.
   CrossRef
2. Hermann Imgartinger,  Peter Walter Fettel, Thomas Escher , Philip Tinnefeld, Simon Nord, and Markus  Saucer “Substituent effects on Redox properties and photoinduced electron transfer in Isoxazolo Fullerenes,” Eur. J.Org.Chem., vol.2000, pp 455-465, January 2000.
   CrossRef
3. David Pegu and Ngangbam Bedamani Singh, “Quantum Chemical Calculations of Molecular Structure, Electronic, Thermodynamic and Non-linear optical properties of 2-amino-3-nitro-6-methylpyridine,”Int.J.Advanced Research, vol.1, issue 9, pp 531-538, November 2013.
4. M. J. Frisch, et al., GAUSSIAN 09, Revision A. 9, Gaussian, INC, Pittsburgh, 2009.
5. M. Silverstein, G.C. Basseler, C. Morill, Spectrometric Identification of Organic Compounds, Wiley, New York, 1981.
6. J. Sharmi Kumar, T. S. Renuga Devi, G. R. Ram Kumaar, A.Bright, “Ab initio and density functional theory calculations of molecular structure and vibrational spectra of 4-(2-Hydroxyethyl) piperazine-1-ethanesulfonic acid,” Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy, vol.152, pp 509-522, July 2015.
   CrossRef
7. N. Sundaraganasan, G. Elango, S. Sebastian, & P. Subramani, Ind. J. Pure App. Phy. 47 (2009) 481.
8. K. Sambathkumar, S. Jeyavijayan, M. Arivazhagan, Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 147 (2015) 124.
   CrossRef
9. S.Gunasekaran, S.Seshadri, S.Muthu, Indian J.Pure and Applied Physics, vol.44, pp360-366, 2006.
10. D. Lin-Vein, N.B. Colthup, W.G.Fateley, J.G.Grasselli, “The Handbook of Infrared and Raman Characteristics Frequencies of Organic Molecules, Academic Press, San Diego, CA, 1991.
11. M. Murugan, V.Balachandran and Marana, “Vibrational spectra and electrostatic potential surface of 2-fluoro-6-methoxybenzonitrile based on quantum chemical calculations,” J. Chemical and Pharmaceutical Research, vol.4, issue 7, pp 3400-3413, 2012.
12. A.A. Popov, V. M. Senyavin, A.A. Ganovsky, Chem.Phys.Lett, 383 (2004) 149-155.
    CrossRef
13. R. S. Mulliken, J. chem. phys., vol 23, pp 1833-1840, 1985.
    CrossRef
14. Isa Sidir, Yadigar Gulseven Sidir, Mustafa Kumalar, Erol Tasal, “Ab initio Hartree-Fock and density functional theory investigations on the conformational stability, molecular structure and vibrational spectra of 7-acetoxy-6-(2, 3-dibromopropyl)-4, 8-dimethyl conmarin molecule,” J. Mol. Struct. Vol.964 pp 134-151, February 2010.
    CrossRef
15. Li Xiao-Hong, Liu Xiang-Ru, Zhang Xian-Zhou, “Calculation of vibrational spectroscopic and NMR parameters of 2- Dicyanovinyl-5-(4-N, N- dimethyl aminophenyl) thiophene by ab initio HF and density functional methods,” Comput.Theor.Chem. vol. 969, pp 27-34, August 2011.
    CrossRef
16. J.A. Alanso , L.C. Balbas and A.Rubio, “ Non local functional for exchange and correlation in density functional theory Application to atoms and to small atomic clusters,” Int. J. Quantum Chem. Vol. 56  pp 499-508, September 2004.
    CrossRef
17. Basak Kosar, C. Albayrak, “Spectroscopic investigations and quantum chemical compound study of (E) -4-methoxy-2-[p-tolylimino) methyl] phenol,”Spectrochim Acta,vol. 78A, pp 160-167,  January  2011.
    CrossRef
18. Zeynep Demircioglu, Cigdem Albayrak, Orhan Buyukgungor, “Experimental (X-ray, FT-IR and UV-Vis spectra) and theoretical methods (DFT study) of  (E)-3 –methoxy -2-[p- tolylimino) methyl ] phenol,” Spectrochim Acta, vol. 128A, pp 748-758, July 2014.
    CrossRef
19. Mauricio Alcolea Pala fox,“Scaling factors for the prediction of vibrational spectra. I. Benzen molecule,” Int. J. Quantum Chem. Vol. 77,pp 661-684, March 2000.
    CrossRef
20. I. Khan, A.Ahmad, J.Phys.chem.solid 74 (2013) 1818.
    CrossRef

---

This work is licensed under a Creative Commons Attribution 4.0 International License.