Lithium Including Mixed Sodium Inside Graphene Oxide (GO) as Anodic Electrodes for Ion Batteries

Introduction

Sodium-ion battery is a type of re-chargeable battery which uses sodium-ions as its charge carriers and is very similar to LIBTs in many ways. Na ions are 33% larger in diameter and 2.1 times heavier within lower gravimetric capacities than Li-ion batteries¹. In addition Na metals are more active than Li with the standard electrode potentials which is ~0.3V higher than Li.

By the Sony it has been realized a commercialization of xC6/Li _1-x CoO2 cells¹ reaction and mechanism in 1991. LIBs are representative energies storage devices based on electrochemical energies, widely used in small grid storage systems. Within discovery of high quality reversible, low-voltage¹ Li-intercalations carbonaceous¹ material, the suitable electronic and chemical performances of LIBs concerning energies and power densities¹, as well as the progress in the cell designing and manufacturing, has been made LIBs extremely successful for mobile equipment.

Although; the Na+ cation has a greater radius than the Li+ cation, that causes a few of the superior LIB anode’s materials un-suitable for [NIBs]², concerns regarding² the extra availability of lithium resources² is raising. A Sodium² ion battery has drawn increasing attention³ due to Na is an mineral abundant³ element and shares² common properties within Li^2-4. Specially, graphite⁵ is used⁶ for anodic electrodes in the present commercial⁷ LIBs, while those have been reported for having a very low capacity⁶ of when used as an anodic electrode for NIBs^5-7.

Both disordering carbons and Nano-flakes⁸ (CNFs) exhibited a high Na intercalation⁹ capacities and emerges⁸ as the leading candidates for NIB applications^8,9 . In this study we tried to build a model for GO for investigating the mechanisms for Na intercalation⁹ into the layered domains⁹. Although, the mechanism⁷ of Na+ cation inserting into disturbed carbons are still controversial¹⁰. It is confirmed that a bigger interlayer distances¹¹ of those carbons, which are bigger than interlayers distances of graphite, help Na+ ion intercalation. Consequently, the defects might be enhanced the Na+ intercalations through the strong bonding energies for overcoming the van der Waals energies between graphene sheets¹². In this study it has been evaluated the reliabilities of several semi-empirical corrections and vdW exchange’s correlation functional for determining the optimal¹² methods of this work. Graphited electrodes are currently the most general materials used for the anodes of commercial¹² batteries due to its capabilities for reversible¹² lithium intercalation¹³ in a layered crystal that represent maximum theoretical Sodium’s storage capacity¹³.

NIBs includes of a positive electrode(+) and a negative electrode(-) with suitable conducting electrolytes where store¹⁴ electric energies as the forming of Na-intercalations compounds¹¹. Electrodes¹², separator¹³, and electrolytes are the major components¹⁴ in the NIB batteries which the anodic electrodes play important behavior in the mechanism of those kind devices^12,13.

The structures and properties¹⁴ of graphitic oxide depends on a synthesis method or degree of oxidation¹³. In addition graphite, typically preserves¹⁴ the layer structures of those parent graphite, but the layers are buckled¹⁴ and the interlayer’s spacing¹⁴ is about two times bigger than the graphite that provides suitable environment for sodium diffusion in a NIBs¹¹

The detailed¹⁵ structures are still not described because of the strong disordering and irregular¹³ packing of those layers¹². GO layer is about 1.1 ± 0.2 nm thick^10,11. STM spectroscopy indicates the presences of some regions¹⁴ where the oxygen atoms are arranged¹² in a rectangular¹³ pattern within lattice constant¹⁴ 0.26 nm × 0.42 nm¹¹ the edges¹⁵ of one layer is terminated with COOH and CO groups¹⁰. GO exfoliates¹⁵ and decomposes¹⁶ when heated (rapidly) at moderately¹⁴ high temperatures within the formation¹⁴ of finely dispersed¹³ amorphous carbons, somewhat similar for activating carbon¹².

XRD¹⁴, FTIR¹⁵, Raman¹⁶, XPS¹⁵, AFM¹⁴, TEM¹³, etc. are some general techniques for characterizing the GO samples¹³. Since the distributions of oxygen’s functionalities on GO sheets are poly-disperse fractionations methods using emulsion¹⁶ stabilizations can be used for characterizing and separating “GO” on the basis of oxidation¹⁴. During of the charging step, the “NIBs” Sodium ions released¹⁵ from the cathodes electrodes to move inside the electrolyte and is inserted¹⁶ into the anodes. Upon¹⁵ discharging, Sodium ions are extracted¹⁵ from the anode electrodes and move back to the cathode¹⁴. Although the electrolytes establishes¹⁵ high ionic conductivities between anodes and cathodes, this electrolyte is not responsible¹⁵ for the conduction¹⁶ of those electrons¹⁶ and the half of reaction, so will move through the extra¹⁴ external wires.

Several experiments¹⁶ have been performed for confirming the utilization of graphene nano-sheets¹⁶ and nano-ribbons¹⁷ for enhancing lithium capacity to improve the recharge cyclic performances. Furthermore semi-empirical¹⁵ and molecular¹⁷ orbital calculations have been used for investigating sodium ion storage states among the graphene sheets¹⁵, as well as some heteroatom-substituted carbon materials¹⁶. There are several studies on anodic materials^17-20 and most of them focus on carbons and inorganic materials¹⁸.

Discharging and charging of LIBTs in graphitized¹⁹ carbon is well investigated up to now^21-24. It has also been established how the repulsive¹⁹ interaction can result in the pure stages during intercalation²². Although efforts have been tried for finding suitable replacements²³, now days only the carbonaceous goods are used for the commercial anodes²⁵. Carbonaceous properties widely depends on the preparing materials such as precursor or heat treatment²⁶

By this work, charging or dis-charging of Na-cations have been investigated²⁴ in Graphite oxide (GO) with the (+) electrode reaction²⁵ as: NaCoO2 ⇄ Na1-x CoO2 + x Na+ + xē and the (-) electrode mechanism as: xGO+ x Na⁺ + xē ⇄ x NaGO_, while the whole reaction is: NaCoO2 + x GO  ⇄ Na_1-xCoO2+ x Na GO.  It has been predicted that a sodium atom is stored²⁶ through two mechanisms: intercalation²⁶ and alloying²⁷. GO similar Graphite is applied as small band gap semi-metals because of its excellent conduction treatment under the influence²⁷ of electrical fields^{28, 29.} Interlayer forces³⁰ are nothing, and the distances among GO layers³¹ are large allowing²⁹ Na-ions for diffusing between GO sheets²². Electrical conductivity of the Na-GO increases, Because of the electron donor nature of the Na³³. Based on some previous studies we have used several methods to simulate the NIBs and calculated the NMR, solvent effect²⁴, voltages, charges and physical properties of our model^{32-43and77-81} .Typical commercially³¹ used sodium -ion battery including several interconnected³² electrochemical cells, where each one consist of a GO anode, a cathode formed³⁰ by sodium metal oxide (NaCoO2) and electrolyte same as NaPF6 embedded in a separator felt²⁹.

Na⁺ Diffusion

Diffusion of Na⁺ in the cells determine the key performance³¹ of Na-ion batteries cells, with the charge and discharge rates, practical and cycling capacities and stabilities respectively. The governing⁴⁵ equations describing⁴⁴ the diffusion⁴⁴ process are famous as Fick’s law as:

which “j_i” is an ion in flux condition, molcm⁻² s⁻¹, D_i are diffusivities of solute (i=1,2), cm² s⁻¹and C_i are concentrations of species i, (molcm3)44. The proportionalities44 factors D are the diffusivities or diffusion coefficients as

In condensed systems both liquid & solid, diffusion⁴⁵ is governed⁴⁵ by random particles, leads to a position exchanges by its neighbor. The kinetic parameter of these processes are temperatures depend to an Arrhenius types relationships

In liquid phase, the temperature related of diffusion⁴⁵ is less than the solid form. There are no successful⁴⁴ first-principle calculations which have been made, because of in-sufficient interpretation of the liquid structure⁴⁴  . Therefore, an easy expression⁴⁴ is gotten from Stoke’s drag law which is used as an alternative⁴⁵ for a diffusivities expression in the liquids⁵⁵ frequently (Eq. 3). Na⁺ is quite big comparing to electrons⁴⁶; the radius of a Na-ion is larger than that of an electron (electron: 10⁻²² m)⁴⁶. The motions of Na-ions are strongly impeded through the ions as discussed below⁴⁷.

Cathode Materials

In an extended approach they can be classified as 1- Layered compounds NaMO2 (M = Co, Ni, Mn), 2- Spinel compounds NaM2O4 (M = Mn, etc.) 3– Olivine compounds NaMPO4 (M = Fe, Mn, Ni, Co, etc.). When a Na-ion diffuses⁵⁶ out of the cathode during the charges cycles the valence states of the transition⁴⁶ metal ion change as; the Fe2+ to Fe3+. The reaction in cathode can be written as: (Fig.1)

NaFePO₄ – xNa⁺ – x e^–  ⇄ x NaPO₄ +(1-x) NaPO₄ and Fe²⁺– e^– ⇄ Fe³⁺

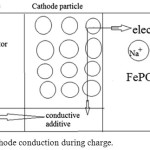Figure 1: The cathode conduction during charge. Click here to View figure

 

Anode Materials

In the anode, Na+ are found to be the suitable electropositive particles with large reversible capacities. However, due to safety considerations⁵¹, metallic Na has been substituted by various carbonaceous materials such as GO. GO-sodium anode has much lower gravimetric and volumetric energies density than pure sodium which leads toward the development of 3d transition metal oxides⁵¹. (M_xO_y, M = Fe, Co, Ni, Mn, Cu). These materials are able to incorporate more than one Na+ per metal through conversion reactions giving higher capacities in comparison to carbon anodes⁵¹. During discharge, Na+ ion is extracted⁵² from the internal layered of graphite, those passes through the electrolyte⁶³ and intercalated between the NaCoO2 compounds Figure.2.

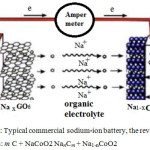Figure 2a: Typical commercial sodium-ion battery, the reversible process is: m C + NaCoO2 NanCm + Na1-nCoO2 Click here to View figure

 

Carbon-sodium anodes have much lower gravimetric and volumetric energy densities than pure sodium which lead towards the development of interstitial-free 3d transition metal oxides

Electron Density Profiles

It has been defined⁵³ as

Where η_i is occupation⁶⁴ orbitals (i), φ is the wave functions of the orbitals, χ and C are basis function and coefficient matrix respectively. Atomic units can be explicitly rewritten as follows (e/Bohr³).

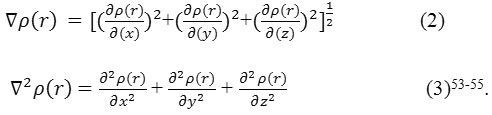
Electron localization⁶⁴ and chemical reactivity has been described by Bader⁶⁶.

Hamiltonian kinetic energy density K(r)

It is defined, since the expected values of kinetic energies operator

can be rewritten by definitions⁵³. One of commonly used definition⁵⁵ is:

“G(r)” is a positive definition of kinetic energy densities.

K(r) and G(r) are related to Laplacian electrons density⁵⁵

ELF or Electronic localization function

Becke and Edgecombe⁵⁷ exhibited that spherically averages like-spin pair probability^56,57 are localization functions

Where

and

For close-shell system, since

D and D0 terms can be simplified as

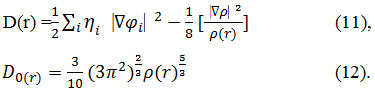
Savin et al. have reinterpreted^67,68 ELF is a meaningful^68,69 for Kohn-Sham^69,70 DFT or even post-HF wave-function⁵⁸.

LOL is the other function in tight localization regions⁶⁸ same as ELF, Schmider&Becke paper^59,60.

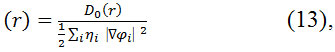
Wher

D_o (r) for spin-polarized and close-shell systems as the same way as in ELF⁶¹.

Local Information Entropy

This entropy is defined as exclusive spaces through minimizing informationentropy⁶² by  Parr et al^63,64.The formula of Shannon’s information⁶⁴ entropies for normalized and continuous probabilities function is

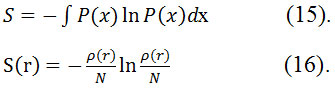
Electrostatic potential (ESP)

The total electrostatic potential measures the set of functions as GIPF⁷⁵ which for the molecular surfaces and macro properties^{65, 66}. There are a lot of reviews on ESP, interested readers are suggested to consult^{66, 67.}

It is accurate in normal cases. Reduced -density -gradient or RDG and Sign (l2)*r are a couple parameter for revealing of the weak interaction region⁶⁸. The basic applications are exemplified in Sections 4.100.1 and 4.200.1. RDG is defined as

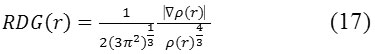
By default x is 0.05, it can be nullify this treatment by setting the parameter to zero.

is an averaged electron density of atom A.

Computational Details

Calculations are performed using both Gaussian and GAMESS-US packages⁶⁸. Pm6, Extended-Huckel and Pm3MM including pseudo=lanl2 calculations⁶⁹.

M06 and m06-L (DFT) functional is based on pseudo-potentials^69-70. The (PBE)⁷¹ exchange-correlations functional are made via minimization of the whole energy^69-71. We employed DFT with the van der Waals densities for modeling the van der Waals capacitor⁷² in the medium-range⁷³ interactions such as the interactions⁷⁴ of two cylinders. In some further calculation the interaction energy between x sodium and GO sheets. The interaction energy was calculated via the Mp6 method in all items according to

ΔE_s (eV) = { E_total ^_ (E_xNa + E_GOsheets )} + E_BSSE

Where the “ΔE_s” is the stability energy of system⁷³.

Result and Discussion

The Laplacian of electron density via Eqs (7, 8) for the Sodium diffused in the GO system which are arranged and listed in table.1. We have used

Table 1: Density, energies, G(r), K(r)and U(r) for 7 sodium insertion

ρ^s (r) = ρ^α (r) – ρ^β (r)

then the polarization-spin valuable will be replaced instead of spin densities

ELFs, Localized locators (LOLs) and Local Entropies including ESP charges, potential energies, of two graphene layers (GO sheets) have been listed in tables1-2 and these data have been plotted in seven figures figs.1-7.The values of ξ yielded from zero to the local region of un-polarized cases, are shown as a complete polarized situation and are listed in (Table1).

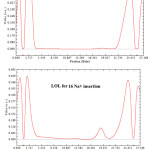Figure 3: ELF, LOL, K(r) and G( r) for 16 Na+ insertion between two layers of GO sheets.   Click here to View figure

 

Figure 4: LOL for various insertion of Na+ between two layers of GO Click here to View figure

 

Kintic energies, Lagrangien kintic energies densities, and the electrostatic potentials can be calculated as eqs. (9), (10) and:

where RA and ZA denotes vectors charges of atom A, and are listed in tables 1,2.

If pseudo-potentials are used, Z is shown the explicitly expression of those electrons. Z can be stand for the atomic charges (the fourth column), at this item V_nu is useful for analyzing the differences between exact electrostatic potential and the electrostatic potential reproduced by atomic charges. Notice that at nuclear positions, this function will be infinite and may cause some numerical problems in program; hence at these cases this function always returns 1000 instead of infinity.

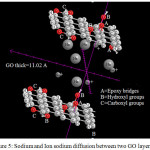Figure 5: Sodium and Ion sodium diffusion between two GO layers Click here to View figure

 

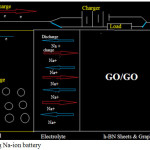Figure 6: Operating Na-ion battery Click here to View figure

 

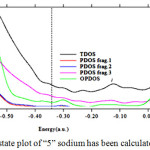Figure 7: Density of state plot of “5” sodium has been calculated of diffusion inside GO Click here to View figure

 

In which the actual kinetic energy term in D (r) from eqs. 15-16 is replaced by Kirzhnits type gradient expansions, which is

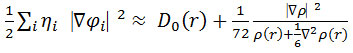
so that ELF is the kinetic energy term.

In this work we have calculated the local information entropies for each Sodium atom via eqs. 19-20 and the   integrating of this function over total space yields the entropy. The calculated data for local entropy are listed in Tables 2-5

Table 1: Density, energies, G(r), K(r)and U(r) for 7 sodium insertion

Na	Alpha(α)	Beta(β)	G(r)	K(r)	U(r)
Na(1)	0.4604895515E-06	0.4604895515E-06	0.5744381519E-05	– 0.3117752101E-06	– 0.5432606309E-05
Na(2)	0.2096714075E-05	0.2096714075E-05	0.1167764372E-04	0.3597110963E-06	-0.1203735482E-04
Na(3)	0.3170935798E-05	0.3170935798E-05	0.2997362700E-04	-0.4869104958E-05	-0.2510452204E-04
Na(4)	0.2724083172E-05	0.2724083172E-05	0.5506029806E-04	-0.4894711288E-05	-0.5016558677E-04
Na(5)	0.3552291679E-06	0.3552291679E-06	0.9933364631E-05	-0.1527079624E-05	-0.8406285007E-05
Na(6)	0.1939734653E-05	0.1939734653E-05	0.1510844208E-04	-0.9991542452E-06	-0.1410928784E-04
Na(7)	0.3182517515E-05	0.3182517515E-05	0.6263968474E-04	-0.1207120164E-04	-0.5056848310E-04

 

Table 2: Electron localization function (ELF), Localized orbital locator (LOL) and RDG for 7 sodium insertion

Na	H(r)	(ELF)	(LOL)	(RDG)
Na(1)	0317752101E-06	02781474745E-09	0.4357352365E-04	0.4198893007E+02
Na(2)	-0.3597110963E-06	0.3494449162E-07	0.2680478226E-03	0.3073178053E+02
Na(3)	0.4869104958E-05	0.583654322E-07	0.2080980347E-03	0.3688949858E+02
Na(4)	0.4894711288E-05	0.194139806E-07	0.8795808397E-04	0.6126518415E+02
Na(5)	0.1527079624E-05	0.1182183375E-09	0.1635044084E-04	0.1358456203E+03
Na(6)	0.9991542452E-06	0.2729617300E-07	0.1819939949E-03	0.4296852960E+02
Na(7)	0.1207120164E-04	0.2114921285E-07	0.1001944131E-03	0.5308390511E+02

 

Weak interactions (eqs 20-21) have significant influences for conformational structures of the macromolecules, however reproduction by the electron density via abinitio.

As sodium have unpaired electrons, leading to a difference in spin-up &down, when two Sodium atoms are adsorbed.

As a result, spin polarized cluster for NIBTs have a gap which size depends on adsorbed spin polarization. And this system can be replaced with LIBTs completely with high performance.

Conclusion

In conclusion, our calculations have been designed to study the Na adsorption on graphene oxide with two layers of GO. Our results exhibit that adsorption in GO is much stronger than pristine graphene.

Additionally, it has been found the structure of GO can be to improve the electrical transport in NIBs. Therefore, the modification and design of GO structure provide strategies for improving the performance of GO-based anodes. With the increase in defect density by GO sheets, maximum capacities obtained are much higher than that of graphite.

References

1. Z. G. Yang, J. L. Zhang, M .C .W. Kintner-Meyer, X. C. Lu, D. W. Choi, J. P. Lemmon, and J. Liu,  Chem. Rev. (2011), 111, 3577–3613.
   CrossRef
2. P. Barpanda, G. Oyama, S.-I. Nishimura, S.-C. Chung and A. Yamada, Nat. Commun. , 2014, 5, 4358.
   CrossRef
3. M. D. Slater, D. Kim, E. Lee and C. S. Johnson, Adv. Funct. Mater. , 2013, 23, 947.
   CrossRef
4. N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Chem.Rev. , 2014, 114, 11636.
   CrossRef
5. P. Ge and M. Fouletier, Solid State Ionics, 1988, 28, 1172.
   CrossRef
6. D. Stevens and J. Dahn, J. Electrochem. Soc., 2001, 148, A803.
   CrossRef
7. Y. Mizutani, T. Abe, M. Inaba and Z. Ogumi, Synth. Met., 2001, 125, 153.
   CrossRef
8. D. Stevens and J. Dahn, J. Electrochem. Soc., 2001, 148, A803.
   CrossRef
9. D. Stevens and J. Dahn, J. Electrochem. Soc., 2000, 147, 1271.
   CrossRef
10. Schniepp, H. C.; Li, J. L.; McAllister, M. J.; Sai, H.; Herrera-Alonso, M.; Adamson, D. H.; Prud’Homme, R. K.; Car, R.; Saville, D. A.; Aksay, I. A. The Journal of Physical Chemistry, (2006) B 110 (17): 8535–8539.
    
11. Pandey, D.; Reifenberger, R.; Piner, R.. Surface Science, (2008), 602 (9): 1607.
    CrossRef
    
12. Talyzin, A. V.; Szabó, T. S.; DéKáNy, I.; Langenhorst, F.; Sokolov, P. S.; Solozhenko, V. L. The Journal of Physical Chemistry C (2009). ,113 (26): 11279.
    CrossRef
    
13. M. Daniela C, K. Dmitry V, B. Jacob M,S. Alexander,  S. Zhengzong,  S. Alexander,  A. Lawrence B,  L. Wei,  T. James. ACS Nano, (2010), 4 (8): 4806–4814.
    
14. Kumar, Harish V.; Woltornist, Steven J.; Adamson, Douglas H. Carbon.2015.10.083.
    
15. T. Suzuki, T. Hasegawa, S. R. Mukai, and H. Tamon, Carbon,2003, 41:1933-1939
    CrossRef
16. T. Hasegawa, T. Suzuki, S. R. Mukai, and H. Tamon, Carbon, 2004, 42:2195-2200.
    CrossRef
17. M. Noel, and V. Suryanarayanan, Journal of Power Sources , 2002, 111, 193–209.
    CrossRef
18. J. L. Tirado, Materials Science and Engineering R , 2003, 40, 103–136.
    CrossRef
19. L.J. Fu, H. Liu, C. Li, Y.P. Wu, E. Rahm, R. Holze, and H.Q. Wu, 2006, Solid State Sciences, 8 113–128.
    CrossRef
20. E. Frackowiak, and F. Béguin, Carbon , 2002, 40, 1775–1787.
    CrossRef
21. M. S. Whittingham, and A.J. Jacobson (Eds.), Intercalation Chemistry, Academic Press (1982).
22. S.A. Safran, and D.R. Hamann, Physical Review Letters. 1979, 42  (21), 1410–1413.
    CrossRef
23. M.D. Levi, D. Aurbach, J. Maier, Journal of Electroanalytical Chemistry 624, (2008) 251–261.
    CrossRef
24. H. Zabel, S. A. Solin (Eds.), Graphite Intercalation Compound I, Springer-Verlag, (1990).
    CrossRef
25. Y.P. Wu, E. Rahm, and R. Holze, Journal of Power Sources , 2003, 114, 228–236.
    CrossRef
26. J.K. Lee, K.W. An, J.B. Ju, B.W. Cho, W.I. Cho, D. Park, and K.S. Yun, Carbon , 2001,39, 1299–1305.
    CrossRef
27. C. De las Casas, and W.Z. Li, J. Power Sources, 2012, 208, 74–85.
    CrossRef
28. K.S. Novoselov, A.K. Geim, S.V. Morozov, D. Jiang, Y. Zhang, S.V. Dubonos, I.V.
29. Grigorieva, and A.A. Firsov, Science 2004, 306 , 666–669.
30. B. Partoens, and F.M. Peeters, Physical Review B , (2006), 74, 075404-1–075404-11
    CrossRef
31. Monajjemi, M.; Lee, V.S.; Khaleghian, M.; B. Honarparvar, B.; F. Mollaamin, F. J. Phys.Chem C. 2010, 114, 15315
    CrossRef
32. Monajjemi, M. Struct Chem. 2012, 23,551–580
    CrossRef
33. Monajjemi, M.;  Boggs, J.E.  J. Phys. Chem. A, 2013, 117, 1670 −1684
    CrossRef
34. Monajjemi, M. Chemical Physics. 2013, 425, 29-45
    CrossRef
35. Monajjemi, M.; Wayne Jr, Robert. Boggs, J.E.  Chemical Physics. 2014, 433, 1-11
36. Tahan, A. Acta Biotheor, 2011, 59, 291–312
    CrossRef
37. Mollaamin, F.; Monajjemi, M. Physics and Chemistry of Liquids .2012, 50,  5,  2012, 596–604
38. Khosravi, M.; Honarparvar, B.; Mollaamin, F.; International Journal of Quantum Chemistry, 2011, 111, 2771–2777
    CrossRef
39. Monajjemi, M.  Theor Chem Acc, 2015, 134:77 DOI 10.1007/s00214-015-1668-9
    CrossRef
40. Monajjemi, M.  Journal of Molecular Modeling , 2014, 20, 2507
    CrossRef
41. Monajjemi, M.  Biophysical Chemistry. 2015 207,114 –127
    CrossRef
42. Physics and Chemistry of Liquids. 2011, 49 (5), 561-571
    CrossRef
43. Jalilian,H.; Monajjemi, M. Japanese Journal of Applied Physics. 2015, 54, 8, 08510
44. Majid Monajjemi *, Samira Bagheri, Matin S. Moosavi, Nahid Moradiyeh, Mina Zakeri, Naime Attarikhasraghi, Nastaran Saghayimarouf, Ghorban Niyatzadeh, Marzie Shekarkhand, Mohammad S. Khalilimofrad, Hashem Ahmadin and Maryam Ahadi, Molecules 2015, 20, 21636–21657; doi:10.3390/molecules201219769
    CrossRef
45. Monajjemi, M, Journal of Molecular Liquids, 2017, 230, 461–472
    CrossRef
46. D.S. Wilkinson, Mass Transport in Solid and Fluids, Cambridge University Press, (2000).
    CrossRef
47. H. Mehrer, Diffusion in Solids, Springer, 2007, pp. 27–36.
    CrossRef
48. D.A. Porter, K.E. Easterling, Phase Transformations in Metals and Alloys, 2nd edition, Chapman & Hall, 1992, pp. 1–109 .
    CrossRef
49. R.H. Petrucci, W.S. Harwood, General Chemistry, 7th edition, Prentice-Hall, 1997, pp. 315–343.
50. H. Dehmelt, Physica Scripta 1998, T22 102–110.
51. C. Wang, and J. Hong, Electrochemical and Solid-State Letters,2007, 10 (3) A65–A69.
52. R.A. Huggins, in: C.A.C. Sequeira, A. Hooper (Eds.), Proceedings of the NATO Advanced Study Institute on Solid State Batteries, Alcabideche, Portugal, September 2–17, (1984).
53. P. Poizot, S. Laruelle, S. Grugeon, L. Dupont, and L.J.M. Tarascon, Nature, 2000, 407, (6803), 496-499 .
    CrossRef
54. A.V. Churikov, N.A. Gridina, N.V. Churikova, in: V. Igor, Barsukov, S.Christopher, Johnson, E. Joseph, Doninger, Z. Vyacheslav, Barsukov (Eds.), New Carbon Based Materials for Electrochemical Energy Storage Systems, Springer,2006, pp. 269–276.
55. T. Lu, F. Chen, Acta Chim. Sinica, 2011, 69, 2393-2406.
56. T. Lu, F. Chen, J. Mol. Graph. Model , 2012,(38): 314-323.
    CrossRef
57. T. Lu, F.Chen Multiwfn: A Multifunctional Wave-function Analyzer, J. Comp. Chem, 2012, (33) 580-592.
58. R.F.W. Bader, atoms in Molecule: A quantum Theory (Oxford Univ. press, Oxford, (1990).
59. Becke and Edgecombe J. Chem. Phys,1990, 92, 5397.
60. A. Savin, Angew. Chem. Int. Ed.Engl,1992, 31, 187.
    CrossRef
61. V.G. Tsirelson, Yu.A. Abramov. Chem. Phys. Lett, 2002, 351, 142–148.
    CrossRef
62. H.L. Schmider ,A.D. Becke J Mol Struct ,Theochem,2000, 527:51 50 .
63. Jacobsen Can. J. Chem., (2008), 86(7), 695.
64. C. Aslangul, R. Constanciel, R. Daudel and P. Kottis. Adv. Quantum Chem ,1972, 6,93.
    CrossRef
    
65. R.G.Parr, P.W.Ayers, R.F.Nalewajski J Phys Chem A,2005, 109:3957–3959.
    CrossRef
66. S. Noorizadeh and E. Shakerzadeh , Phys. Chem. Chem. Phys.2010, 12, 4742.
    CrossRef
67. J.S.Murray, and P. Politzer, J. Mol. Struct. (Theochem),1994, 307, 55.
    CrossRef
68. J. S. Murray Comput. Mol. Sci., 2011, 1, 153.
    CrossRef
69. P. Politzer, J. S. Murray, Theor. Chem.  Acc. 2002, 108 134 .
70. M.W. Schmidt, K.K.Baldridge, J.A.Boatz, S. T. Elbert, M. S. Gordon, J . H. Jensen, S. Koseki, N. Matsunaga, and K. A. Nguyen et al 2004,14(11) 1347–1363.
71. Yan Zhao, Donald G. Truhlar,  Theor Chem Account , 2008,120 215–241 .
    CrossRef
72. W. Kohn, L. J. Sham, Phys. Rev. 1965, 140 A 1133-1138 .
73. J.P. Perdew, K.Burke , Ernzerhof, Phys. Rev. Lett. ,1996, 77, 3865-3868.
    CrossRef
74. D. L. Klein, R. Roth, A. K. L. Lim, A. P. Alivisatos, and P. L. McEuen, Nature, 1997, (London) 389-699 .
75. Yan Zhao, Donald G. Truhlar, Accounts of Chemical Research, 2008, 41(2) 157-167.
    CrossRef
76. B.H. Besler, K.M. Merz, P.A. Kollman, J. comp. Chem. 1990, 11 431.
77. L.E. Chirlian, M. M. Francl, J.comp.chem.,1987, 8 894.
78. Brneman GM, Wiberg KB J. Comp Chem 1990, (11): 361
79. Jalilian, H.; Monajjemi, M.; Aghaei, H, ORIENTAL JOURNAL OF CHEMISTRY, 2017, 33, (5)  2179-2187
80. Raoufi, F.; Aghaie, H.; ORIENTAL JOURNAL OF CHEMISTRY, 2017, 33, 5, 2542-2550
81. Mohammadian ,N.; Zare, K.; Monajjemi, M.; ORIENTAL JOURNAL OF CHEMISTRY, 2017, 33, No. 4,1595-1602
82. Chitsazan,A.;  Monajjemi, M.; Aghaei, H.; Sayadian, M.; ORIENTAL JOURNAL OF CHEMISTRY, 2017, 33, No. (3): 1366-1374
83. Moosavi, M.S.; Monajjemi, M.; Zare, K.; ORIENTAL JOURNAL OF CHEMISTRY, 2017, 33, No. 4, 1648-1658

---

This work is licensed under a Creative Commons Attribution 4.0 International License.