ISSN : 0970 - 020X, ONLINE ISSN : 2231-5039
     FacebookTwitterLinkedinMendeley

Non Bonded Interactions in a Cylindrical Capacitor of (M, N) @ (M', N') @ (M”, M”) three Walled Nano Carbon Nanotubes

Volume 33, Number 6

Nabieh Farhami, Majid Monajjemiand Karim Zare

Department of Chemistry, Science and Research Branch, Islamic Azad University, Tehran, Iran.

Corresponding Author E-mail: m_monajjemi@srbiau.ac.ir

DOI : http://dx.doi.org/10.13005/ojc/330640

Article Publishing History
Article Received on :
Article Accepted on :
Article Metrics
ABSTRACT:

In this study we have exhibited that there are regular non-bonded interactions among the layers of Three walled Carbon nanotubes (TWCNTs) and (10, 10), (8, 8) DWCNTs & (6,6) SWBNNTs. It has been observed the energies between three layers are sensitive to chirality dramatically. In other hands the external fields of the inner tubes make strongest fields for the outer tubes. It has been shown the non-bonded quantum mechanics in terms of wave functions and charges densities between three layers. For the systems including charges Q the densities (|ψ(x)2|) multiplied the atomic charges, yielding toward the charges densities of (|ψ(x)2|.

KEYWORDS:

Non-covalent interaction; three walled Nano tubes; cylindrical capacitor

Download this article as: 

Copy the following to cite this article:

Farhami N, Monajjemi M, Zare K. Non Bonded Interactions in a Cylindrical Capacitor of (M, N) @ (M', N') @ (M”, M”) three Walled Nano Carbon Nanotubes. Orient J Chem 2017;33(6).

Copy the following to cite this URL:

Farhami N, Monajjemi M, Zare K. Non Bonded Interactions in a Cylindrical Capacitor of (M, N) @ (M', N') @ (M”, M”) three Walled Nano Carbon Nanotubes. Orient J Chem 2017;33(6). Available from: http://www.orientjchem.org/?p=40754

Introduction

Three walled nanotubes (T-WCNTs) can be considered as a tube twisted from hexagon sheets of graphene or boron nitrides plates which have been synthesized1 in 1995 firstly. Boron nitrides tubes have structural analogs as carbon nano tubes. SWBNNTs, in contrast of CNTs is metallic or semiconductors depends on its chirality1, boron nitrides tube are occasionally believed2 to be a 1-dimension insulators regarding of their helicity3, tube’s diameter and the number of tubes wall4.

Since BNNTs were synthesized1 via arc5 discharges successfully, the mechanism6 for its formations are obscure7 yet, and the behaviors of the metallic catalyst remain an unknown question7.

Several experiment results showed which small CNTs are occasionally found inside three-walled tubes8-12. Therefore, there are strong motivations for studding in phenomenon of their stabilities in small BNNTs inside the largest one12-15, which might be helping the experimental11 synthesis12-14. Besides15, Studding on Three-walled NNTs (TWNTs) has demonstrated14,15 interesting16 variations in their electronics properties17 when they are compared18 with those of freestanding17,18 components . Therefore it is also important for seeing the inter-walled coupling18 behaviors associated with those small BNNTs19,20.

Internal-layers couplings play a critical19 function for determining properties21 of layered three-dimensional22 material. Truly, the novel studies have exhibited which mechanical20 coupling among the outer and inner shells of T-WCNTs leads19,20 for characterizing radials-breathing20 vibration that corresponds to oscillated modes21 with concerted22 inner-and outer-shells motion.

Fig.1. (10,10),(8,8),(6,6) TWCNTs in view point of Cartesian orientation Figure 1:(10,10),(8,8),(6,6) TWCNTs in view point of Cartesian orientation 

Click here to View figure
Fig.2. (10, 10), (8, 8)DWCNTs &(6,6) SWBNNTs in view point of Cartesian orientation Figure 2: (10, 10), (8, 8)DWCNTs &(6,6) SWBNNTs in view point of Cartesian orientation 

Click here to View figure

 

It has been exhibited which TWCNTs are having high oxidative resistance21, which were later confirmed23, by other scientists. Recently, some results indicate which purified22 SWBNNTs are resist for oxidase up to 1,100°C23. Furthermore, SWBNNTs are predicted to have piezoelectricity24 character and are applicable25 for room-temperatures hydrogen26 storages.

An elastic26 property of an individual SW-BNNT has been clearly studied through thermal vibration27 methods.

SWBNNTs were theoretically predicted28 the uniforms electronics properties29 which are related to its chirality and also diameters2,3.In addition, zigzags chiral are expected28 for having direct28 bands gaps. Other word, the armchairs tubes shall have in directs band28 gaps. Due to their large band gaps using MWBNNTs as the conduction29 channel for fields-effects transistors29 indicated that MWBNNTs allowed transports through the valence29 bands. Important points concerning the bands gap for boron nitrides Nano tube are that those are tunable12,13 via doping15 with carbons. Theoretical band gaps and densities of states calculation in point of view Fermi17-29 level suggested27,28 that SWBNNTs can either be p – types or n – types semiconductor through controlling24-28 the composition33 of carbons into SWBNNTs .

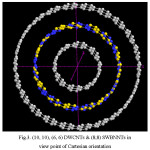Fig.3. (10, 10), (6, 6) DWCNTs & (8,8) SWBNNTs in view point of Cartesian orientation Figure 3: (10, 10), (6, 6) DWCNTs & (8,8) SWBNNTs in view point of Cartesian orientation 

Click here to View figure
Fig.4. Color-Field map of electron density versus atomic position Figure 4: Color-Field map of electron density versus atomic position 

Click here to View figure

 

The piezoelectricity approaches originated34 from the deformations effects because of twisting of the h-BN planes for forming the tubes structures. It is an important behavior in BNNTs24. It has been exhibited that BNNT can be amazing piezoelectric24 system while the piezoelectric constants for different zigzags BNNT was defined for increasing along25 with the decreases of the radiuses of BNNTs25. One of the most important features of BNNTs is that BNNTs possess large band gaps between 5.0 and 6.0 electron volte irrespective29 of the number of BNNT’s wall, diameter and chirality2,16-27 .

In this study we have exhibited that there are regular18 non-bonded interactions among the layers of TWCNTs and it has been observed the energies between three layers are sensitive to chirality dramatically12. In other hands the external fields of the inner tubes make strongest fields for the outer tubes.

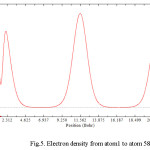 Fig.5. Electron density from atom1 to atom 588 Table.1.Cartezian and charge density of atoms 550 to 588 and HOMO/LUMO gaps Figure 5: Electron density from atom1 to atom 588
Click here to View figure
Table.1.Cartezian and charge density of atoms 550 to 588 and HOMO/LUMO gaps Table 1: Cartezian and charge density of atoms 550 to 588 and HOMO/LUMO gaps 

Click here to View table
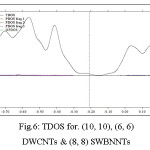 Fig.6: TDOS for. (10, 10), (6, 6) DWCNTs & (8, 8) SWBNNTs Figure 6: TDOS for. (10, 10), (6, 6) DWCNTs & (8, 8) SWBNNTs 

Click here to View figure

 

It has been shown the non-bonded quantum mechanics in terms of wave functions and charges Q the densities (|ψ(x)2|) multiplied the atomic charges, yielding toward the charges densities of |ψ(x)2|. Therefore, there are good relationships among charge and wave functions of those inner tubes rather than outers . Although the wave functions of each molecule in the systems for ΦnInnertube and Φmoutertube under the permutations of electrons coordinate is anti-symmetric, the product of those non-bonded molecule under intermolecular exchanges of the electron  could not be anti-symmetric.

The unique solution for this purpose is introducing the intermolecular anti-symmetrize operators. However, these would results due two major problem which were shown by Eisenschitz38 , that are, the anti-symmetrized unperturbed state no longer eigen-function of  H(0), which will be followed via the [Ã,H(0)]≠0, hereby the projected excited state, ÃInn-outΦnInn Φmout,become linearly dependent38,39 . and the first-order energies including exchanges could be written as:
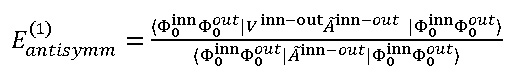
Formula
Generally, the exchange interactions are commensurate19 to the differential overlaps among other parts. The wave-function as well as the exchange interactions fades exponentially as functions of distance38,39 .Therefore, TWCNNs with small diameter and short distance between three layers have been considered based on our previous works30-49.
Computational details

Calculations were accomplished by Gammas package50. In this study, we have calculated for getting the result from DFT method and extended-hackles approaches for the no-bonded interactions among tubes. The m06-2x, and m06HF are new method with suitable corresponds in no-bonded interactions and are important for the distance calculations among fragments in the non-bonded51 systems, for medium51 (∼3–5Å) . We investigated density functional theories with theory of van der Waals densities for modeling exchange-correlations energies for the nanotubes3-22. The double ζ-basis set including polarize orbitals was used for boron and nitrogens atoms while single ζ-basis set including polarize orbital was applied for the TWCNTs, respectively53.

For non-covalent interactions, the BLYP methods are unable for describing van der Waals51-53 TWCNTs systems by medium-ranges interaction such as interaction between three tubes of TWCNTs. The B3LYP and some other functional are not suitable for illustrating the exchanges and correlations energies in distant medium-range non-bonded system obviously. In addition, some novel studies have exhibited that inaccuracies of the medium-ranges exchanges energies lead to a systematic error to predict of molecular properties53-58 .

Geometry optimization and electronic structures have been accomplished using the semi empirical methods such as CNDO, MINDO, and ZINDO which their approach  are  based  on  an  semi empirical  solution ab-initio and  the Kohn-Sham  equation57  also. The  density function  theories  in  the plane-waves  sets  with  the  projector-augmented  wave  pseudo-potential are calculated. The Perdew-Burke-Ernzerhof58exchange-correlations functional for the generalized gradient approximations or GGA are adopted58. The optimization of the lattices constant and the atomics coordinate are made through the minimization of those total energies.

The charges transferring and electrostatic potentials-derived were also calculated using the Merz-Kollman-Singh59, chelp60, or chelpG61.
The charges calculations method based on molecular electrostatics potentials fitting are not complete-suited for estimating of bigger systems which some of those inner-most atom are located62 far away from that point at which the MESP62 is computed60-62. In these conditions, variation of the inner-most atomics charge would not leads to a significant change of the MESP61 outside of the molecules, meaning where the accurate62 value for the innermost atomics charge  are not well-determined by MESP62  outside63 of those  molecules .The representatives atomics charge for molecule must be computed as averages value over various molecules and conformation. A detailed overview of those effect of those basis sets on the charges distribution might be found in63,64 . It has been extracted the charges densities profile from the first-principle calculations through the average process described65,66.

The interaction energies for capacitors were calculated through equation: ΔEs (eV)= {ETWCNT-(ESWCNT(1)+ESWBNNT(2)+ ESWCNT(3))}+ EBSSE where the “ΔEs ” are the stabilities energies of non-bonded interactions in TWCNTs.
Result and Discussion

The results are plotted in 6 curves and HOMO LUMO is listed in Table1.

We have estimated the electron densities and  Gradient norms & Laplacians, values of orbitals wave-functions, electron spin densities, electrostatic potentials from nuclear / atomics charge, electron localization functions or ELF64-66, localized orbitals locator or LOL64-66  defined via Becke & Tsirelson, total electrostatics potentials , and the exchange-correlations densities, correlations hole and correlations factor, Averages local ionization energies using the Multifunctional66 Wave-functions Analyzer65,66 Through Density-of-state DOS66 it has been represented the number of state in the units energies intervals, since energies level are contiguous, so DOS66 has drawn as curves map. The systems are isolated, so the energies levels are discrete66.

We have investigated the DOS66 graphs as the tools for analyzing the natures of electron structures in the nanotubes. The original total DOS (TDOS) of our system have calculated based on TDOSE(E) = Σi δ(E-εi) where ε eigenvalue set of single-particle Hamilton is,  is Dirac Delta function which after replacing Gaussian, it can be yielded63.
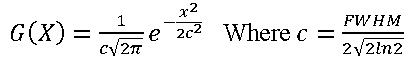
Formula
FWHM63 is acronyms of “full width at half maximum63, it is an adjustable parameter in multi-wave function, the larger FWHM the TDOS analysis is easier for performing. The normalized Lorentzian function is defined as L (X) = FWHM/2π 1/x2 +0.25FWHM2 Pseudo-Voigt function is weighted linear combination for Gaussian function and Lorentzian formula: P(x) = wgaussG(x)+(1-Wgauss)L(x).

The curve map of broadened partial DOS (PDOS) and overlap DOS (OPDOS) are valuable for visualizing orbital composition analysis, PDOS function of fragment A is defined as: PDOSA(E) = Σi Ξi,A F (E-εi) where is the composition of fragment “A” in orbital i. The OPDOS among fragments A and B are defined as OPDOSA,B(E)= ΣiXiA,B F (E-εi) where Xi A,B A, B is the composition of total cross term between fragment A and B in orbital i .

Both original and broadened TDOS/PDOS/OPDOS are shown in the graph below. The original DOS graphs are discrete comb-like lines, from which we cannot obtain any additional information other than energies level distributions, it is impossible for distinguishing different types of a line and degenerate energies levels owing for overlapping.

From the height of black curves (TDOS) we can clearly know how dense the energies levels are distributed everywhere. Besides, the curves corresponding to TDOS, PDOS (red line for fragment 1, blue line for fragment 2) and OPDOS (green line) no longer overlap, we can clearly identifies characters of each orbitals through observing those curves67-69.

References

  1. Chopra, N. G., Luyken, R. J., Cherrey, K., Crespi, V. H., Cohen, M. L., Louie, S. G., and Zettl, A., Science 1995, 269, 966-7
    CrossRef
  2. A. Rubio, J. L. Corkill, and M. L. Cohen, Phys. Rev. B , 1994, 49, 5801
  3. X. Blase, A. Rubio, S. G. Louie, and M. L. Cohen, Europhys. Lett. 1994, 28, 335
    CrossRef
  4. L. F. Sun, S. S. Xie, W. Liu, W. Y. Zhou, and Z. Q. Liu, Nature ,2000, 403, 384
    CrossRef
  5. X. Zhao, Y. Liu, S. Inoue, T. R. Suzuki, O. Jones, and Y. Ando, Phys. Rev. Lett.2004,92, 125502
    CrossRef
  6. L. Guan, K. Suenaga, and S. Iijima, Nano Lett.2008 8, 459
    CrossRef
  7. S. Okada, S. Saito, and A. Oshiyama, Phys. Rev. B 65, 2002,165410.
    CrossRef
  8. Levshov, D.; Than, T. X.; Arenal, R.; Popov, V. N.; Parret, R.; Paillet, M.; Jourdain, V.; Zahab, A. A.; Michel, T.; Yuzyuk, Y. I., et al., Experimental Evidence of a Mechanical Coupling between Layers in an Individual Double-Walled Carbon Nanotube. Nano Lett. 2011,11, 4800-4804.
    CrossRef
  9. Liu, K. H.;Hong, X. P.; Wu, M. H.; Xiao, F. J.; Wang, W. L.; Bai, X. D.; Ager, J. W.; Aloni, S.; Zettl, A.; Wang, E. G., et al., Quantum-Coupled Radial-Breathing Oscillations in Double-Walled Carbon Nanotubes. Nat. Commun. 2013,4, 1375.
    CrossRef
  10. D. Golberg , Y. Bando , K. Kurashima and T. Sato , Scripta Mater. 44 (2001) 1561
    CrossRef
  11. Y. Chen , J. Zou , S. J. Campbell , and G. L. Caer , Appl. Phys. Lett, 2004, 84 ,2430
    CrossRef
  12. C. Y. Zhi , Y. Bando , C. C. Tang , R. G. Xie , T. Sekiguchi and D. Golberg , J. Am. Chem. Soc.2005, 127,15996
    CrossRef
  13. E. J. Mele and P. Kral, Phys. Rev. Lett. 2002, 88 ,56803
    CrossRef
  14. S. M. Nakhmanson , A. Calzolari , V. Meunier , J. Bernholc and M. B. Nardelli ,2003, Phys. Rev. B 67, 235406 .
    CrossRef
  15. S. H. Jhi and Y. K. Kwon, Phys. Rev. B.2004. 69 , 245407
    CrossRef
  16. N. G. Chopra and A. Zettl , Solid State Commun, 1998,105 , 297.
    CrossRef
  17. A. Loiseau , F. Willaime , N. Demoncy , G. Hug and H. Pascard , Phys. Rev. Lett. 1996, 76 , 4737
    CrossRef
  18. M. Radosavljevic , J. Appenzeller , V. Derycke , R. Martel , Ph. Avouris , A. Loiseau , J.-L. Cochon and D. Pigache , Appl. Phys. Lett.2003,  82,4131
    CrossRef
  19. Y. Miyamoto, A. Rubio, M. L. Cohen and S. G. Louie, Phys. Rev. B , 1994, 50,4976
    CrossRef
  20. E. J. Mele and P. Kral , Phys. Rev. Lett. , 2002, 88 (2002) 56803 .
  21. S. M. Nakhmanson , A. Calzolari , V. Meunier , J. Bernholc and M. B. Nardelli , Phys. Rev. B ,2003, 67, 235406 .
    CrossRef
  22. Blase, X., Rubio, A., Louie, S. G. & Cohen, M. L. Quasiparticle band structure of bulk hexagonal boron nitride and related systems. Phys. Rev. B , 1995, 51, 6868
    CrossRef
  23. Xiang, H., Yang, J., Hou, J. & Zhu, Q. First-principles study of small-radius Single-walled BN nanotubes. Phys. Rev. B , 2003, 68, 035427
    CrossRef
  24. R. Eisenschitz and F. London, Z. Physik 60, 491(1930) and Z. Physik.Chemie, 1937, 33, 8-26
  25. O. Hirschfelder, C. F. Curtiss, and R. B. Bird, Molecular Theory of Gases and Liquids, Wiley, New York, 1954
  26. Monajjemi, M.; Najafpour, J. Fullerenes, Nanotubes, and Carbon Nanostructures, 2014, 22(6): 575–594
    CrossRef
  27. P. Pyykkö, C. Wang, M. Straka , and J. Vaara, Phys. Chem. Chem. Phys. 9, 2007, 2954-2958 (2007).
  28. C. Wang, P. Pyykkö, and M. Straka, Phys. Chem. Chem. Phys. 2010, 12, 6187-6203
    CrossRef
  29. Mahdavian, L.; Monajjemi, M.; Mangkorntong, N. Fullerenes, Nanotubes and Carbon Nanostructures, 2009, 17 (5), 484-495
    CrossRef
  30. Monajjemi,M.; Nayyer T. Mohammadian J. Comput. Theor. Nanosci. 2015, 12, 4895-4914.
    CrossRef
  31. Monajjemi, M.; Lee, V.S.; Khaleghian, M.; B. Honarparvar, B.; F. Mollaamin, F. J. Phys.Chem C. 2010, 114, 15315
    CrossRef
  32. Monajjemi, M. Struct Chem. 2012, 23,551–580
    CrossRef
  33. Monajjemi, M.;  Boggs, J.E.  J. Phys. Chem. A, 2013, 117, 1670 −1684
    CrossRef
  34. Monajjemi, M.; Khaleghian, M, Journal of Cluster Science. 2011, 22 (4),673-692
    CrossRef
  35. Monajjemi, M.; Wayne Jr, Robert. Boggs, J.E.  Chemical Physics. 2014, 433, 1-11
  36. Monajjemi, M. Falahati, M.; Mollaamin, F.; Ionics, 2013, 19, 155–164
    CrossRef
  37. Monajjemi, M.; Mollaamin, F. Journal of Cluster Science, 2012, 23(2), 259-272
    CrossRef
  38. Tahan, A.; Monajjemi, M. Acta Biotheor, 2011, 59, 291–312
    CrossRef
  39. Mollaamin, F.; Monajjemi, M. Physics and Chemistry of Liquids .2012, 50,  5,  2012, 596–604
  40. Monajjemi, M.; Khosravi, M.; Honarparvar, B.; Mollaamin, F.; International Journal of Quantum Chemistry, 2011, 111, 2771–2777
    CrossRef
  41. Monajjemi, M.  Theor Chem Acc, 2015, 134:77 DOI 10.1007/s00214-015-1668-9
    CrossRef
  42. Monajjemi, M.  Journal of Molecular Modeling , 2014, 20, 2507
    CrossRef
  43. Monajjemi, M.; Khaleghian, M.; Mollaamin, F.   Molecular Simulation. 2010, 36, 11,  865–
  44. Monajjemi, M.  Biophysical Chemistry. 2015 207,114 –127
    CrossRef
  45. Jalilian,H.; Monajjemi, M. Japanese Journal of Applied Physics. 2015, 54, 8, 08510
  46. Monajjemi, M.; Mollaamin, F. Journal of Computational and Theoretical Nanoscience, 2012, 9 (12) 2208-2214
    CrossRef
  47. Mollaamin F, Varmaghani Z, Monajjemi M. 2011; 49: 318-336.
  48. Mollaamin, F.;  Baei, MT.;  Monajjemi, M.; Zhiani, R.;  Honarparvar, B.;49. Russian Journal of Physical Chemistry A, Focus on Chemistry, 2008, 82 (13), 2354-2361
    CrossRef
  49. M Monajjemi, L Mahdavian, F Mollaamin, B Honarparvar,Fullerenes, Nanotubes and Carbon Nanostructures,2010, 18 (1), 45-55
    CrossRef
  50. Schmidt MW,Baldridge kk,Boatz, Elbert ST, Gordon Ms, Jensen JH, Koseki S, Matsunaga N,Nguyen KA, J Compt chem, 2004, 14(11)1347
  51. Yan Zhao, Donald G. Truhlar, Theor Chem Account (2008) 120:215–241
    CrossRef
  52. Yan Zhao, Donald G. Truhlar, Accounts of Chemical Research, 2008, 41, 2, 157-167
    CrossRef
  53. Check, C. E.; Gilbert, T. M. J. Org. Chem , 2005, 70, 9828–9834
    CrossRef
  54. Grimme, S. Seemingly. Angew. Chem., Int. Ed. 2006,45, 4460–4464.
    CrossRef
  55. 55.Wodrich, M. D.; Corminboeuf, C.; Schleyer, P. v. R.. Org. Lett. 2006, 8, 3631–3634.
    CrossRef
  56. Schreiner, P. R.; Fokin, A. A.; Pascal, R. A., Jr.; de Meijere, A. Org. Lett. 2006, 8, 3635–3638.
    CrossRef
  57. W. Kohn and L. J. Sham, Phys. Rev. 1965,140 A 1133-1138
  58. Perdew J P, Burke K and Ernzerhof, Phys. Rev. Lett. 1996, 77, 3865-3868
    CrossRef
  59. B.H. Besler, K.M. Merz, and P.A. Kollman, J. comp. Chem.1990, 11, 431
  60. L.E. Chirlian and M.M. Francl, J.comp.chem.1987, 8, 894.
  61. C.M. Brneman and K.B. Wiberg, J. Comp.Chem.1990, 11, 361
    CrossRef
  62. F. Martin, H. Zipse, J. Comp. Chem.2005, 26, 97 – 105
    CrossRef
  63. Balderchi, A.; Baroni, S.; Resta, R. Phys. Rev. Lett. 1988, 61, 173.
    CrossRef
  64. Tian Lu, Feiwu Chen, Sinica, 69, 2011, 2393-2406
  65. Tian Lu, Feiwu Chen, J. Mol. Graph. Model, 2012, 38, 314-323
    CrossRef
  66. Tian Lu, Feiwu Chen, Multiwfn: A Multifunctional Wave-function Analyzer,  J.Comp. Chem. 2012, 33, 580-592
    CrossRef
  67. Monajjemi, M. Falahati, M.; Mollaamin, F.; Ionics, 2013, 19, 155–164
    CrossRef
  68. Monajjemi, M., Chahkandi, B. Journal of Molecular Structure: THEOCHEM, 2005, 714 (1), 28, 43-
  69. M Monajjemi, L Mahdavian, F Mollaamin, B Honarparvar,Fullerenes, Nanotubes and Carbon Nanostructures,2010, 18 (1), 45-55.
    CrossRef

Creative Commons License
This work is licensed under a Creative Commons Attribution 4.0 International License.