Optimization for the Simultaneous Determination of Zinc in Environmental Samples With Calcon by Adsorptive Stripping Voltammetry: Response Surface Methodology

Introduction

Heavy metal contamination in the environment is a major concern worldwide because of toxicity of these metals and their potential threat to human health. Currently, quantification of heavy metals relies upon the collection of liquid discrete for subsequent laboratory analysis using techniques such as ICP-MS, AAS, GC, HPLC, FT-IR, and GS/MS¹, but these instruments too expensive and are not practically applied especially in Indonesia. Therefore, the analysis is often limited to laboratory level. Since such requirements are greatly met with electrochemical methods.

Electrochemical methods are widely used in the field of analytical chemistry is sensitive, selective, simple, less costly and less time consuming², simplicity, fast response, and suitability for the preparation of inexpensive and portable instrumentations³. Therefore we need a sensitive and selective method for determining the levels of trace amounts of metal ions, namely the adsorptive stripping voltammetry (AdSV). Adsorptive stripping voltammetry is chosen as an alternative method because it has many advantages including: high salt content from seawater not disturbing in analysis, high sensitivity, low detection limit on µg/L scale (ppb), easy use and easy sample preparation, rapid analysis, inexpensive infrastructure^4-12. In addition, by this method, it is possible to study the chemical specimens of heavy metals¹³, which can not be done by other methods. The toxicity of heavy metals is determined from its chemical species^14-15. Almost all methods of determining metals in very small quantities require considerable time at the pre-concentration stage before measurement. In voltammetric stripping adsorptive pre-concentration phase time is shorter, generally less than 1 minute^{7-8, 12, 16}.

The previous research, to find the optimum condition, determination of metal ions Cd, Cu, Pb and Zn¹⁷ and Fe, Co, Ni and Cr¹⁸ in either singular or simultaneous form of AdSV, is done by observing the effect of one of the variables being changed while the other variable is kept at a constant level. This optimization technique is called the optimization of one variable or one factor at that time.

The weakness of the optimization of one factor is that optimization does not take into account the interaction effects between the variables studied. Therefore, this technique does not describe the full effect of parameters on the response^19-22. Another disadvantage of one-factor optimization is an increase in the number of experiments required to conduct research, leading to increased time and increased consumption of reagents and materials. To overcome this problem, an analytic procedure optimization technique is needed by using RSM.

AdSV is a highly sensitive and selective technique^{7-8, 21-22}, the response obtained in the form of peak current (Ip) is strongly influenced by the following variables, namely, the calcon concentration, pH, potential accumulation and time accumulation. Therefore, it is important to determine the optimization of these parameters, which will affect the measurement of peak currents in order to improve the quality of the analysis results²³. However, in order to reach such a high sensitivity, the experiment must be carefully designed and important experimental factors, which can affect both response and accuracy, need to be optimized. A well-designed experiment can provide signals with superior quality compared to those measured without optimization^24-25.

The purpose of this research is to get the optimum condition of Zn metal ion, so it can be applied to the analysis of the metal in environmental samples (seawater, fresh water, tap water, vegetables, and fruits) simultaneously. To achieve that goal, an analytical procedure optimization technique is required using RSM with CCD^19-29. The analytic parameters of the Zn metal ions are determined as follows: detection limits, linear range, correlation coefficient, recovery and relative standard deviation (RSD).

Experimental Details

Material and Instruments

To the vessel voltammeter, 10 mL of mixed standard solutions of Cd(II), Cu(II), Pb(II) and Zn(II) 10 µg/L were added 0.2 mL KCl 0.1M and 0.2 mL 20 mL of solution.

The Instrument used in this research is Metrohm 797 Computrace with HMDE working electrode, reference electrode of Ag/AgCl/ KCl, and Pt electrode as supporting electrode; pH meters Griffin model 80, Griffin & George Loughborough, England; and analytical balance of Mettler AE 200, Toledo OH-USA; As well as glass equipment commonly used in laboratories.

General  Procedure

The research design used in this study, as a tool for optimization are CCD with 4 variables, 3 levels/level, and 31 treatment combinations. The first step of 2^k factorial design optimization is code, where the highest level (+1), the lowest level (-1) and code (0) as a center point. The program for statistical data processing is Minitab by using RSM  (Table 1).

Table 1: CCD variable level for independent parameters of the metal ion mixture (Cd, Cu, Pb and Zn).

Factors		Levels  (Cd, Cu, Pb, Zn)
		-1	0	+1
Calcon concentration (mM)	C	0.6	0.7	0.8
pH	pH	5	6	7
Potential accumulation (V)	E	-0.7	-0.6	-0.5
Time accumulation (s)	T	40	60	80

 

Sumber  : level 0  diambil dari penelitian sebelumnya⁴

Calcon concentration, pH, potential accumulation and time accumulation adjusted according to experimental design of CCD in Table 2, below. From Table 2, we get the response of the peak currents of metal ions Cd, Cu, Pb and Zn simultaneously.

Table 2: Experimental design of RSM for optimization simultaneous determination of Cd, Cu, Pb and Zn with Calcon

Run	Factor				Peak current (nA)
	Calcon (mM)	pH	Potential (V)	Time (s)	Cd	Cu	Pb	Zn
1	0.6	5	-0.7	40	21.75	129.74	52.22	57.58
2	0.6	5	-0.5	40	12.17	174.41	54.45	57.16
3	0.6	5	-0.7	80	37.35	178.61	105.90	43.44
4	0.6	5	-0.5	80	11.61	176.06	104.21	49.35
5	0.6	7	-0.7	40	16.36	266.66	40.21	87.60
6	0.6	7	-0.5	40	9.56	284.95	44.71	92.37
7	0.6	7	-0.7	80	23.61	269.02	38.17	77.73
8	0.6	7	-0.5	80	9.45	251.44	75.64	84.67
9	0.8	5	-0.7	40	25.11	180.35	41.40	61.13
10	0.8	5	-0.5	40	13.12	182.27	38.77	54.13
11	0.8	5	-0.7	80	48.71	191.26	79.17	54.13
12	0.8	5	-0.5	80	10.05	176.11	57.54	46.14
13	0.8	7	-0.7	40	92.35	295.00	39.16	83.35
14	0.8	7	-0.5	40	62.63	293.86	37.28	92.71
15	0.8	7	-0.7	80	101.69	313.50	40.20	90.03
16	0.8	7	-0.5	80	70.97	276.99	39.19	105.80
17	0.7	6	-0.6	60	104.33	221.07	80.86	101.49
18	0.7	6	-0.6	60	100.35	231.13	81.85	104.32
19	0.7	6	-0.6	60	105.21	232.14	80.86	105.29
20	0.7	6	-0.6	60	104.12	223.12	79.36	103.41
21	0.7	6	-0.6	60	103.13	222.07	83.14	103.43
22	0.7	6	-0.6	60	102.23	221.32	81.26	102.21
23	0.7	6	-0.6	60	104.12	222.04	81.26	101.21
24	0.532	6	-0.6	60	15.61	204.06	86.38	98.24
25	0.7	4.32	-0.6	60	19,67	201.89	74.87	92.89
26	0.7	6	-0.768	60	28.48	169.23	69.04	84.43
27	0.7	6	-0.6	26,4	12.25	123.32	33.70	88.11
28	0.868	6	-0.6	60	39.90	118.98	45.76	84.98
29	0.7	7.68	-0.6	60	78.77	117.77	69.87	97.65
30	0.7	6	-0.432	60	7.35	226.99	46.84	99.76
31	0.7	6	-0.6	93,6	12.72	186.71	87.97	83.61

 

Determination of Sampling Site and Sample Preparation

The sampling method is done by purposive sampling, which is done by taking into account the condition of the research area also the current and the depth of the research area. This is intended to see to what extent the concentration of pollutants spread. To know the content of heavy metals in sea water is done sampling in sea water taken around Bungus, water tap from research laboratory of Chemistry Department, lake water from Maninjau Lake and river water taken from Lubuk Minturun. Samples of water prior to analysis were preserved with 65% HNO₃ with a ratio of  2: 1000 and filtered using Whatman 42 filter paper³⁰.

Vegetable samples used in this study are, cauliflower, mustard greens, eggplant, and broccoli, while the fruits used include apples, banana kepok, melon and dragon fruit. Samples of vegetables and fruits before the determination of Zn metal content is determined first the water content, then do wet destruction with the addition of nitric acid pa and perchloric acid pa.

Each sample of 0.5000 g was carefully weighed and mashed, put into a Kestergum digestion flask. Further, the wet was destructed by the addition of 5 ml of concentrated nitric acid and 0.5 ml of concentrated perchloric acid, shaken and left overnight. Next, heated to the digestor block starting at 100°C, after the yellow vapor is exhausted the temperature is increased to 200^oC. The destruction is terminated when the white vapor and liquid in the flask remain about 0.5 mL, cooled and diluted with doubly destilled water and the volume is adjusted to 50 mL, shaken until homogeneous and left overnight and disarrayed³².

Clear solution is ready to be determined by Zn metal content with Voltammeter and Atomic Absorption Spectrophotometer as a comparison. The determination of the optimum conditions used in this study is the procedure developed by the previous research team^{4, 7-9, 11-12, 17-18}.

Detection Method

The procedure of determining RSD (relative standard deviation), LOD (limit of detection), LR (linear range) and recovery has been done by previous researchers The procedure of determining RSD (relative standard deviation), LOD (limit of detection), LR (linear range) and recovery has been done by previous researchers^{4, 7-9, 11-12, 17-18}.

Result and Discussions

Optimization of Zinc Using one Variable

The optimization by observing the effect of one  variable in the determination of trace metal Zn  in the presence  of calcon has been done [1]. The optimum condition as follow: calcon concentration 0.7 mM, pH 7,   potential accumulation -0.6 V, time accumulation 70 s. At   the optimum conditions, the relative standard deviation was obtained with 8 replicates (n = 8) measurements standard  solution  Zn(II) 10u g/L was 0.86 %, respectively. This technique does not describe the full effect on the response parameters and optimization of these factors is the increase in the number of trials required to do research, which leads to increased time and increased consumption of reagents and materials. Therefore to overcome this problem, an optimization technique of analytical procedures is by using RSM.

Optimization of Zinc using RSM

The polynomial equations, the effects of calcon concentration (x₁), pH (x₂), potential accumulation (x₃), and time accumulation (x₄) on peak current (ŷ), were obtained using the statistical software package, Minitap release 16.  For an experimental design with four factors, the model includes linier, quadratic, cross terms and can expressed by equation (1):

ŷ =  βo+ β₁ x₁+ β₂ x₂+ β₃ x₃+ β₄ x₄+ β₁₁x₁²+ β₂₂x₂²+ β₃₃x₃²+ β₄₄x₄²+ β₁₂x₁x₂+ β₁₃x₁x₃+ β₁₄x₁x₄+ β₂₃x₂x₃ + β₂₄x₂x₄+ β₃₄x₃x₄

Where ŷ in the AdSV predicted response, x₁, x₂, x₃, and x₄ are the independent variables, βo is intercept (constant), β_i is the linier coefficient, β_ii is the squared coefficient and β_ij is the cross coefficient. The explained  variation percentage was expressed by the the determination coefficient R² at 5% statistical significance level.

The data was processed, which resulting the regression coefficient in the second orde model Table 3.

Table 3: Regression  coefficients in  the second order  model

Term	Coefficient
Constanta	105.833
x1	0.244
x2	14.274
x3	2.912
x4	-2.412
x1*x1	-7.966
x2*x2	-6.672
x3*x3	-7.795
x4*x4	-9.998
x1*x2	1.966
x1*x3	0.180
x1*x4	2.148
x2*x3	2.275
x2*x4	3.068
x3*x4	1.491

 

Based on Table 3, the second order model obtained :

ŷ = 105.833+ 0.244 x1+14.2744 x2+2.912×3-2.412×4-7.966×12-6.672×22-7.795×32 9.998×42+1.966x1x2+0.180x1x3+2.148x1x4+2.275x2x3 +3.068x2x4+1.491x3x4

Table 4: ANOVA second orde model

Sumber	DF	Seq SS	Adj SS	Adj MS	F	P
Regressi	14	10343.5	10343.5	738.82	5.07	0.001
Liniar	4	4723.7	4723.7	1180.92	8.10	0.001
x1	1	1.3	1.3	1.29	0.01	0.926
x2	1	4412.7	4412.7	4412.70	30.27	0.000
x3	1	183.6	183.6	183.63	1.26	0.278
x4	1	126.0	126.0	126.05	0.86	0.366
Square	4	5214.7	5214.7	1303.68	8.94	0.001
x1*x1	1	1436.2	1063.2	1063.21	7.29	0.016
x2*x2	1	957.7	745.9	745.92	5.12	0.038
x3*x3	1	1145.9	1017.9	1017.94	6.98	0.01
x4*x4	1	1675.0	1675.0	1674.95	11.49	0.004
Interaction	6	405.1	405.1	67.52	0.46	0.825
x1*x2	1	61.9	61.9	61.86	0.42	0.524
x1*x3	1	0.5	0.5	0.52	0.00	0.953
x1*x4	1	73.8	73.8	73.79	0.51	0.487
x2*x3	1	82.8	82.8	82.81	0.57	0.462
x2*x4	1	150.6	150.6	150.55	1.03	0.325
x3*x4	1	35.6	35.6	35.58	0.24	0.628
Residu Error	16	2332.5	2332.5	145.78
Lack-of-Fit	10	2319.1	2319.1	231.91	103.61	0.000
Pure Error	6	13.4	13.4	2.24
Total	30	12676.0

 

Based on Table 4, test procedures are performed on the second order model. This hypothesis test is used to test the significance of the regression model, ie to test whether there are free variables (including quadratic and interaction effects) have a significant effect on the response variable.

The hypotheses tested were:

H0: βi = 0,

H1: there is βi ≠ 0; I = 1,2,3, …, k

Based on Table 2, the regression parameter test simultaneously yields p-value of 0.001, meaning that the p-value obtained is smaller than the significance level used by α = 0.05. Thus it is decided to reject Ho and it is concluded that there are independent variables that have a significant effect on the response variable, so that the  second order model can be accepted.

It can be seen (Table 4) the test results for each type of influence independent variable to the response variables include linear, quadratic and interaction effects. The p-value for linear and quadratic effects are 0.001 (smaller than the α level used at 0.05). The effects of these effects (linear and quadratic) have a significant influence on the response variables. In other words, there is at least one linear influential variable and at least one quadratic variable influences the response variable. While for interaction effect test obtained p-value value of 0.825, which means statistically, none of the interaction effects that have a significant effect on the response.

Furthermore,  the indicator of the accuracy of the model, based on the coefficient of determination (R²) obtained a value of 81.60%., Meaning the percentage of the diversity of responses capable of being explained by the second order model is 81.60%. Thus the second order model already has a fairly high level of accuracy. It can also be seen from the plot between the response value (experimental results) with the expected value of response (from the second order model) as can be seen in Figure 1.

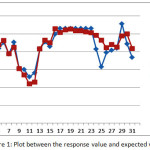Figure 1: Plot between the response value and expected value Click here to View figure

 

From Figure 1, it can be seen that most of the alleged values obtained from the second order model are very close to the true response value. Thus the second order model gives a high accuracy of estimation.

Determination of Stasioner Point

Based on the value of regression coefficient in Table 3 we can compile matrices b and B as follows:

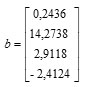
dan

Sehingga diperoleh titik stasioner sebagai berikut:

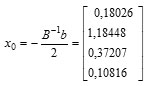
Thus, the response solution at the stationary point is obtained as follows:

Furthermore the stationary point can be returned to the real value, the conditions obtained that provide the optimal solution are as follows:

Table 5: Result of optimum condition of Zn with RSM

Variable	Optimal value (with encoding)	Optimal value (without encoding)
x1	0,18026	0,7018
x2	1,18448	7,1845
x3	0,37207	-0,5628
x4	0,10816	62,1632

 

Where  :   calcon concentration (x₁), pH (x₂), potential accumulation (x₃), and time accumulation (x₄)

Analysis of Response Surface Characteristics

To get an idea of the surface characteristics of the response, we first calculate the eigen value  (λ) of the matrix B and obtain

λ = [ – 10, 8112 – 8,8183 – 7,9457 – 4,8561 ]

Since the four eigen values are negative, the response surface shape is maximum. It can also be viewed from contour plots and surface response plots. By constructing two constants between the 4 factors observed at the stationary point, a contour plot and response surface can be constructed as shown in the figure below.

Based on data analysis with surface response method, it is concluded that peak current will reach maximum value at the time of calcon concentration = 0.7018 mM, pH = 7.1845, potential accumulation -0.5628 V and time accumulatin 62.1632 s. The maximum value of the peak current is 1143.720 nA.

Plot Contour and Surface Response at Stationary Point (Figure  2)

By making a constant of two of the four factors used, it can be shown that the contour and the response surface are the maximum. In Figure 2, the contour plot will be presented and the surface of each possible pair of factors used by taking the condition of another factor is at a stationary point.

Figure 2: it can be seen the range of values of each pair of variables that allegedly will give the maximum value. Click here to View figure

 

As described previously, that at the stationary point obtained an optimum response value of 114.720. As an alternative to achieving the optimum response value, a combination of other values can be used as shown by the innermost circle of the contour plot. All pairs of points that are in this deepest circle are expected to produce a maximum response value with the following details:

Each pair of points in the innermost circle of the plot between x₁ and x₂ will result in a predicted value of  > 100 response

Each pair of points in the innermost circle of the plot between x₁ and x₃ will produce an estimated value of  > 110 response

Each pair of points in the innermost circle of the plot between x₂ and x₃ will produce an estimated value of  > 110 response

Each pair of points in the innermost circle of the plot between x₁ and x₄ will result in a predicted value of  > 100 response

Each pair of points in the innermost circle of the plot between x₂ and x₄ will result in a predicted value of  > 100 response

Each pairs of points in the innermost circle of the plot between x₃ and x₄ will produce an estimated value of  > 110 response

It can be given the choice of alternatives to generate maximum response values, there is flexibility in determining the level of each factor that is thought to be capable of generating maximum response value.

Application Method

To evaluate the validation of the proposed method for the analysis of real samples, the proposed procedure is applied to various samples such as water samples (sea water, tap water, river and lake water), vegetables (cabbage, broccoli, mustard greens, eggplant) (Apple, dragon fruit, melon and banana kepok). The Zinc concentration in the sample can be seen in Table 6. determined by the standard addition method using the recommended procedure under optimum conditions in the sample of vegetables and fruits

Table 6: Comparison of methods of determination of Zn in vegetable and fruit samples

Sample	Metode AdSV (mg/L)	Metode AAS (mg/L)
Broccoli	2.712	1.238
Cauliflower	2.198	1.218
Eggplant	2.153	1.471
Mustard	4.598	1.216
Apples	2.176	1.270
Banana kepok	5.786	1.417
Dragon fruit	7.453	1.241
Melon	4.091	1.232

 

The results from Table 6 show that the AdSV method gives satisfactory results when compared to the atomic absorption spectrophotometer (AAS) method. Furthermore, determination of Zn metal in environmental samples in AdSV by using calcon, can be seen in Table 7.

Table 7: Determination of Zn in environmental samples by AdSV using calcon

Sample	Zn (mg/L)
Broccoli	2.785
Cauliflower	1.88
Eggplant	2.005
Mustard	4.876
Apples	2.105
Banana kepok	7.412
Dragon fruit	7.612
Melon	3.871
Sea water	0.062
Tap water	0.034
Water from Maninjau	0.193
Water from river	0.010

 

Acknowledment

The authors are grateful to  Ministry of Research and Higher Education for supporting this work No : 01/UN.16.17/PP.Proter/LPPM/2017, April 7, 2017.

Conclution

Based on data analysis with RSM, obtained optimum condition of the simultaneous determination zinc, calcon concentration: 0.70 mM, at pH 7.18,  potential accumulation -0,56 V and time accumulation 62.16 sec. From the optimum condition obtained by value of RSD 2.5% with recovery 98.01%, linear range (0.2 -105) μg/L, and LOD 1.21 μg/L. This RSM can be applied to the simultaneous determination of zinc in environmental samples (water: lakes, taps, sea, rivers, fruits: apples, dragon fruit, cantaloupe and banana kepok and vegetables: broccoli, cauliflower, mustard and eggplant) effective.

References

1. Wang, S;  Xu, H;  Li, J. Environmental electroanalytical chemistry. Chinese J.  Anal. Chem. 2002, 30(8),  1005-1011.
2. Gupta, VK; Sethi, B; Sharma, RA; Agarwal, S;  Bharti, A.  Mercury selective potentiometric sensor based on low rim functionalized thiacalix [4]-arene as a cationic receptor. J. Mol. Liq. 2013, 177, 114-118.
   CrossRef
3. Krausa, M; Schorb, K.  Trace detection of 2,4,6-trinitrotoluene in the gaseous phase by cyclic voltammetry. J. Electroanal. Chem. 1999,   1-2, 10-14.
   CrossRef
4. Deswati;  Suyani, H; Safni. The Method of the development of analysis Cd, Cu, Pb and Zn in sea water by adsorptive stripping voltammetry (AdSV) in the presence of calcon as complexing agent. Indones. J. Chem. 2012, 12(1), 20 -27.
   CrossRef
5. Ensafi, A.A., Abbasi, S; Mansour, HR. Differential pulse adsorptive stripping voltammetric determination of copper(II) with 2-mercaptobenzimidazol at Hanging Mercury-Drop Electrode. Anal. Sci. 2001, 17, 609-612.
   CrossRef
6. Zang, S;  Huang, W.  Simultaneous determination of Cd(II) and Pb(II) using a chemically modified electrode. Anal. Sci. 2001, 17, 983-985.
   CrossRef
7. Deswati; Buhatika,C; Suyani, H;   Emriadi; Loekman, U.  Simultaneous determination of copper, lead, cadmium and zinc by adsorptive stripping voltammetry   in  the presence of murexide. Int. J. Res. Chem. Environ.  2014, 4(2),  143 -152.
8. Deswati; Munaf, E; Suyani, H; Loekman, U;  Pardi, H. The sensitive  and simple determination of trace metals Fe, Co, Ni and  Cr in   water   samples   by   adsorptive stripping voltammetry (AdSV) in the presence of calcon. Res. J. Pharm, Biol and Chem. Sci. 2014, 5(4), 990-999.
9. Deswati;  Amelia, L; Suyani, H; Zein, R; Jin, J. Applicability of kalsein in the simultaneous determination of trace metals copper, lead and cadmium by cathodic adsorptive stripping voltammetry. Rasayan. J. Chem. 2015, 8(3), 362-372.
10. Deswati; Suyani, H; Zein, R;  Refilda; Sutopo, J. Application of adsorptive stripping voltammetry for the determination of heavy metals Cd, Cu, Pb and Zn in the culture of fish floating net cages in Maninjau Lake, Agam, West Sumatra, Indonesia. J. Chem, Pharm Res. 2015, 7(8), 942-947.
11. Deswati; Suyani, H; Zein, R; Alif, A; Pardi, H. Applicability of calcein as a chelating agent for simultaneous determination of Cd(II), Cu(II), Pb(II) and Zn(II) in water samples   by adsorptive stripping voltammetry.  J. Chem, Pharm Res. 2015, 7(10), 833 -840.
12. Deswati; Suyani, H;  Zein, R; Alif, A; Pardi, H. Adsorptive stripping voltammetric method for the individual determination of Cd(II), Cu(II), Pb(II), and Zn(II) in vegetable samples using calcein. Rasayan J. Chem., 2017, 10(2), 549-557.
13. Jugade, R.M; Joshi, AP.  Highly sensitive adsorptive stripping Voltammetric method for  the ultra trace determination of chromium(VI). Anal.  Sci. 2006, 22, 571-574.
    CrossRef
14. Proti, P. Introduction to modern Voltammetric and polarographic analysis techniques. Amel Electrochemistry Ed. IV, 2001.
15. Richard,  JC; Martin, J;  Milton, T. Analytical technique for trace element analysis : An overview. Trend in Anal. Chem. 2005, 24(3), 266 – 274.
16. Amini, MK; Kabiri, M. Determination of trace amounts of nickel by differential pulse adsorptive cathodic stripping voltammetry using calcon carboxylic acid as a chelating agent.  J. Iran. Chem. Soc. 2005, 2, 32-39.
    CrossRef
17. Deswati; Suyani, H; Safni; Loekman, U; Pardi, H. Simultaneous determination cadmium, copper and lead in sea water by adsorptive stripping voltammetry in the presence of calcon as complexing agent. Indones. J. Chem., 2013, 13(3), 236 -241.
    CrossRef
18. Deswati; Munaf, E; Suyani, H; Zein, R; Pardi, P.. Simultaneous determination of trace amounts of iron, cobalt, nickel and chromium in water samples with calcon as a complexing agent by adsorptive stripping voltammetry. Asian J. of Chem. 2015, 27(11), 3978-3982.
    CrossRef
19. Deswati; Suyani, H; Zein, R; Izzati Rahmi, HG. Application of respon surface methodology for the determination of cadmium in sea water by adsorptive stripping voltammetry in the presence of calcon.  J. Chem. Pharm. Res. 2015, 7(8), 750 -757.
20. Deswati; Izzati Rahmi, HG; Suyani, H; Zein, R. Respon surface methodology optimization for the determination of zinc in water samples by adsorptive stripping voltammetry. J. Chem. Pharm. Res. 2015, 7(10), 862-870.
21. Deswati; Izzati Rahmi, HG; Suyani, H; Zein, R;. Alif, A. Application of central composite design for optimization the determination of lead  adsorptive cathodic stripping voltammetry. Rasayan. J. Chem.  2016, 9(1), 8-17.
22. Deswati; Izati Rahmi, HG; Suyani, H; Zein, R; .Alif, A.  Optimization central  composite design for the simultaneous determination of Cd(II) ion in fruit and vegetable samples by adsorptive stripping voltammetry. Oriental J. Chem. 2016, 32(3), 1493-1502.
    CrossRef
23. Paolicchi, I; Renedo, OD; Lomillo, MAL; Martinez, MAA. Application of an a optimazation procedure in adsorptive stripping voltammetry for the determination of trace contaminant metals in aqueos medium. Anal. Chim. Acta. 2004, 511, 223 -229.
    CrossRef
24. Morgan, E. Chemometrics: Experimental design , ACOL, Newyork, Wiley, 1991.
25. Jurado-Gonzales, JA; Galindo-Riano, MD; Garcia-Vargas, M. Experimental design in the development of a new method for the sensitive determination of cadmium in sea water by adsorptive cathodic strippping voltammetry. Anal Chim Acta.  2003, 487, 229-41
    CrossRef
26. Izzati Rahmi, HG; Deswati; Suyani, H; Zein, R. Design experiment optimization for the determination of copper in water samples by  adsorptive  stripping voltammetry. Res. J. Pharm, Biol and Chem. Sci.  2016, 7(3), 673-682.
27. Dewi, AK; Sumarjaya, IW;  Srinadi, IGAM. Penerapan metode permukaan respons dalam masalah optimasi. E-Jurnal Matematika. 2013, 2(2),  32-36.
    CrossRef
28. Bezerra, MA; Santelli, RE; Oliveira, EP Villar, LS; Escaleira, LA. Respon surface methology (RSM) as a tool for optimization in analytical chemistry. Talanta. 2008, 76, 965 – 977.
    CrossRef
29. Yilmaz, S;  Ozturk, B;  Ozdemir,D; Eroglu, AE; Ertas, FN. Application of experimental design on determination of aluminum content in saline samples by adsorptive cathodic stripping Voltammetry. Turk. J. Chem. 2013, 37, 316 -324.
30. Ensafi, A.A; Khayamian, T; Benvidi, A; Mirmomtaz, E. Simultaneous determination of copper, lead and cadmium by cathodic adsorptive stripping voltammetry using artificial neural network. Anal. Chimica Acta. 2006, 561, 225-232.
    CrossRef
31. Miller, J.C; Miller, J.N.  Statistics for Analytical Chemistry. Ellis Horwood, New York, 1994.
32. Sulaeman, Suparto and Eviati. Technical guidelines for chemical analysis of soil, plants, water and fertilizers. Agency for Agricultural Research and Development, Ministry of Agriculture. 2005.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.