Tautomeric Study of Neutral, Protonated and Deprotonated Isorhodanine Based on High Level Density Functional Theory

Introduction

Derivatives of rhodanine family, a structurally distinct class of heterocyclic compounds, have accepted important prevalence in medicinal, pharmaceutical chemistry, as well as in the industrial applications^1,2. Of particular interest is their ability to donate electrons toward metal ions, which makes them suitable as ligands in the complexation reaction for use in analytical chemistry as sensitive reagents for the analysis of heavy metals^3,4. Recently, tautomerization of rhodanine family have been theoretically and experimentally studied^5-8. These studies suggested that the dioxo, dithione, oxo/thione and thione/oxo derivatives are the predominant form. Moreover, the intramolecular proton transfer (IPT) process of heterocyclic compounds including, particularly, biologically active compounds, has received a great importance in many fields of chemistry and biochemistry. The term ‘‘tautomerism” refers to a compound existing in an equilibrium between two or more isomeric forms called tautomers⁹.

On the other hand, Protonation and deprotonation reactions (B + H⁺→ BH⁺ and HA – H⁺ → A^–, where B and A are the basic and acidic centers, respectively) play a very  important role in organic chemistry and biochemistry^10,11 and are the first steps in many fundamental chemical rearrangements.^12,13 The capability of an atom or molecule in the gas phase to accept or to lose a proton can be characterized by calculating, from the above reactions, the proton affinity (PA), molecular gas phase basicity (GB) and the deprotontation enthalpy (DH_dep), which give a deep understand of the correlations between molecular structures, molecular stability, and reactivity of the organic molecules.¹⁴ Using standard conditions, The PA is defined as the negative of the enthalpy change associated with the gas phase protonation reaction and the deprotonation energy is defined as the enthalpy change associated with the gas phase deprotonation reaction. Great progress has been made in experimental and theoretical investigations of the protonation and deprotonation of heterocyclic compounds.^15-29 Most of these studies have been carried out to predict the correct protonation and deprotonation sites and the possible role played by the protonation and deprotonation process in the isomerization process.

For this study, one of the rhodanine family,isorhodanine(thiazolidin-2-one-4-thione)compound (Scheme 1), was chosen. Despite the fact that rhodanine family and its derivatives have been extensively studied, there is a paucity of data relating to the  relative  stabilities,  proton  affinities (PAs),  gas  phase  basicity (GBs)  and  the  deprotonation  energy (DH_dep)  of  the  compound  under  probe. To the best of our knowledge, the protonation and deprotonation of the investigated compound have not been reported in the literature. Therefore, our main objectives are of three folds: firstly, to calculate the relative stabilities of the possible tautomeric forms of the compound under probe in its neutral, protonated and deprotonated cases in both the gas- and solution-phase (water), secondly, tocalculate the PA, GB and DH_dep and finally, to study the isomerization process leading from the most stable species to the other tautomericones.

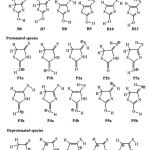Scheme 1: Schematic tautomeric structures of (a) neutral, (b) protonated and (c) deprotonated isorhodanine. Click here to View Scheme

 

Computational Details

All quantum chemical calculations were carried out with the aid of the Gaussian 09 set of programs.³⁰ Geometry optimizations and calculations of harmonic vibrational frequencies of the different species under consideration (Scheme 1) were initially carried out using the hybrid density functional B3LYP, that is, Becke’s³¹ three-parameter nonlocal hybrid exchange potential with the nonlocal correlation of Lee, Yang, and Parr³² with 6-311+G(d,p) basis set. This approach has been shown to yield reliable geometries for a wide variety of systems. The corresponding harmonic vibrational frequencies of the different stationary points of the potential energy surface (PES) were evaluated at the same level of theory in order to identify the local minima and the transition states (TS) as well as to estimate the corresponding zero point energy corrections (ZPE), which were scaled by the empirical factor 0.9806 proposed by Scott and Radom,³³Single point B3LYP calculations with a high level basis set 6-311++G(3df,2p) provided more reliable relative energies for the local minima and transition states. We have  additionally  carried  out  calculations  in  solution  using  the  polarizable  continuum model  (PCM). The proton affinity, gas phase basicity and enthalpy of deprotonation have been calculated based on the mathematical details shown in the literature²⁸. The electronic structure of both neutral, and the protonated species were analyzed by means of the atoms-in-molecules (AIM) theory.³⁴ For this purpose, we have located the bond critical points (BCP) and the ring critical points (RCBs) for the particular case of cyclic systems using of the B3LYP/6-311+G(d,p) level, and evaluated the charge densities at each point. Moreover, we have obtained the corresponding molecular graphs defined by the network of bond paths. To perform the AIM analysis we have used the AIM2000 suite of programs.³⁵

Results and Discussion

Three forms of isorhodanine, neutral, protonated and deprotonated, will be considered in this study classified as follows: For neutral case: five tautomers can be envisaged resulting from 1,3-Hydrogen transfer. Each of these tautomers presents several conformers, resulting from the rotation of the hydrogen atom around the single bond (C4-S7 and/or C2-O6), that lead in total, to eleven structures. So that, eleven structures are presented in Scheme 1.Protonation of the isorhodaninemay take place at two sites:the carbonyl (C2=O6) or thiocarbonyl(C4=S7) groups, leading to structures P1 and P2.Some of thetautomers that result from1,3-hydrogen transferhave been included in this work. In this case, two hydrogentypes could be involved: hydrogen attached to the nitrogen atposition 3 (N3-H8) leading to structuresP3andP5, hydrogen attached tocarbon atom at position 5 (C5-H9(10)), leading to structure P4. In summary, fivetautomers and their five tautomers have been considered (Scheme 1). Deprotonation of the isorhodanine can be accomplished by the elimination of two types of hydrogen: amino hydrogen (N3-H8), leading to structure D1, and hydrogen attached to carbon atom at position 5 (C5-H9(10)) leading to structure D2. Another three tautomers have been included due to 1,3-H transfer marked by D3, D4 and D5 (scheme 1)

Relative Stability

The relative energies, DE,of the neutral, the protonated and the deprotonated species, single point energies, zero point energies, and thermal corrections to energy of all the species under probe in bot gas phase and water are gathered in Table 1. All structures which are listed areenergy minima. Scheme 1 shows schematically the different neutral, protonated and deprotonated species which have been found.Table 1 shows that the oxo/thione forms in all cases (R1, P2b and D1) are the most stable tautomers in both the gas phase and the solution. The calculations predict that the oxo/thione form (R1) is 5.2 kcal mol^-1 more stable than the oxo/thiol form R4. These results are in agreement with the previous results,^5-8,27,28 The protonated and deprotonated oxo/thione forms P2band D1 are thermodynamically more stable than the protonated and deprotonated oxo/thiol forms P4a and D3by 2.5 and 4.6 kcal mol^-1, respectively.

Our results show that the neutral oxo/thiol forms R4 and R5 are more stable other neutral enol/thione and enol/thiol forms; implying that the hydrogen atom during the 1,3-H transfer process prefers to migrate to heteroatom of the thiocarbonyl group (C2=S7) than that of the other heteroatom of the carbonyl group (C2=O6). These results can be explained in terms of the higher polarizability and consequently the size of the sulfur atom than of the oxygen atom. Moreover, from the gathered results in Table 1, the stability trend of the neutral species is R1 >R4 >R3>R8 > R6> R10.

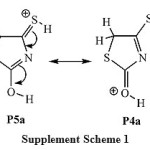
For protonation species (Table 1), the results of the relative stabilities of the different protonated species show that the relative stability order of the most stable protonated tautomers is as follow: P2b > P3b > P4a  » P5a > P1a. It is found that tautomer P2b, which is produced by the direct protonation of the heteroatom of thiocarbonyl group C4=S7,is predicted to be 6.6 kcal mol^-1 more stable than the tautomer P1b, which is produced by the direct protonation of the heteroatom of the carbonyl group C2=O6.These results can be will understood if one considers that sulfur has larger size and lower electronegativity so it better accommodates the positive charge of the conjugate acid stabilizing the system. This means that, in agreement with a similar heterocyclic systems,²⁸ the thiocarbonyl group C4=S7 is the preferred site for the protonation; implying that isorhodanine compound is a sulfur base. The most stable enol/thione and one/thioltautomers are, respectively, P3a and P5a. Importantly, the structuresP4andP5are almost energetically degenerate. This degeneracy can be explained in terms of the resonance that exit between the two tautomers, see the supplement scheme S1 for P4a«P5a resonance structure.

Table 1: Gas and solvent phase single point energy (E in hartree), zero point energy (ZPE in hartree), thermal correction to energy (TCE) in hartree, and relative energies, (DE in kcal mol^-1) of neutral, protonated and deprotonated isorhodanine.

	Gas				water
	Ea	ZPEb	TCEb	DEc	Ea	ZPEb	TCEb	DEc
neutral
R1	-1042.6537	0.0625	0.0688	0.0	-1042.6640	0.0624	0.0687	0.0
R2	-1042.6322	0.0585	0.0652	8.8	-1042.6465	0.0586	0.0653	6.6
R3	-1042.6335	0.0586	0.0653	8.1	-1042.6459	0.0586	0.0652	6.8
R4	-1042.6385	0.0587	0.0656	5.2	-1042.6487	0.0586	0.0655	5.3
R5	-1042.6385	0.0587	0.0656	5.2	-1042.6487	0.0586	0.0655	5.3
R6	-1042.6241	0.0619	0.0683	17.9	-1042.6359	0.0617	0.0680	16.8
R7	-1042.6174	0.0616	0.0681	21.8	-1042.6332	0.0615	0.0680	18.3
R8	-1042.6223	0.0583	0.0653	15.0	-1042.6290	0.0581	0.0651	17.1
R9	-1042.6220	0.0585	0.0654	15.3	-1042.6295	0.0583	0.0652	17.0
R10	-1042.6165	0.0579	0.0652	18.3	-1042.6267	0.0580	0.0651	18.5
R11	-1042.6158	0.0580	0.0652	18.8	-1042.6273	0.0582	0.0652	18.3
Protonated
P1a	-1042.9710	0.0744	0.0811	6.6	-1043.0611	0.0749	0.0814	9.6
P1b	-1042.9662	0.0741	0.0808	9.3	-1043.0586	0.0744	0.0811	10.7
P2a	-1042.9746	0.0713	0.0781	0.6	-1043.0700	0.0719	0.0786	0.4
P2b	-1042.9755	0.0713	0.0781	0.0	-1043.0710	0.0720	0.0787	0.0
P3a	-1042.9743	0.0712	0.0783	0.8	-1043.0525	0.0715	0.0781	10.9
P3b	-1042.9743	0.0712	0.0783	0.8	-1043.0595	0.0717	0.0788	7.1
P4a	-1042.9701	0.0709	0.0781	3.1	-1043.0542	0.0713	0.0780	9.6
P4b	-1042.9701	0.0709	0.0781	3.1	-1043.0585	0.0714	0.0785	7.3
P5a	-1042.9715	0.0714	0.0780	2.5	-1043.0520	0.0714	0.0781	11.2
P5b	-1042.9705	0.0714	0.0781	3.2	-1043.0525	0.0715	0.0781	10.9
Deprotonated
D1	-1042.1239	0.0492	0.0554	0.0	-1042.2055	0.0492	0.0553	0.0
D2	-1042.1152	0.0494	0.0557	5.7	-1042.1977	0.0495	0.0557	5.3
D3	-1042.0936	0.0450	0.0519	14.3	-1042.1778	0.0453	0.0520	12.9
D4	-1042.0763	0.0487	0.0551	29.4	-1042.1699	0.0490	0.0553	22.2
D5	-1042.0921	0.0449	0.0518	15.1	-1042.1777	0.0452	0.0519	12.8

^a at B3LYP/6-311++G(2df,2p)//B3LYP/6-311+G(d,p) level of theory

^batB3LYP/6-311+G(d,p) level of theory

^cDE = E+ZPE*0.9806+TCE

 

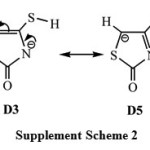
For the deprotonation species, the calculations expect that the global minimum corresponds to the tautomer D1 in which the deprotonation process takes place by the elimination of the hydrogen atom (H8) of the amino group N3-H8. The tautomer D2, in which the deprotonation process occurs by the elimination of the hydrogen atom of the methylene group C5-H(9)10. Gas phase relative energies results show that D2 is 5.7kcal mol^-1 less stable than D1. Interestingly, D1 form is found to be highly stable by about 14-29 kcal mol^-1 than the oxo/thiol and enol/thione forms (D3, D4 and D5), implying that D1 tautomer is the predominant in the gas phase. It is worth mentioning that nitrogen is more electronegative  compared with carbon so it better accommodates negative charge of the conjugate base stabilizing the anionic system. Therefore, the relative stability trend of the deprotonated species in the gas phase is as follow: D1 > D2 > D3 » D5 > D4. It is worth to mention that the tautomeric forms of D3 and D5 are almost degenerate, leading the one to expect a resonance structure. See the supplement scheme S2.

Scheme 1a Click here to View Scheme

 

Scheme 2a Click here to View Scheme

 

In  order to confirm the above mentioned results, the proton affinities (PAs), molecular basicity (GB) and the deprotonation enthalpy (DH_dep) valueshave been calculating the B3LYP/6.-11++(3df,2p)//B3LYP/6.-11+(d,p level of theory. Previous studies showed that the proton affinity values computed using density functional theory are as effective as high level ab initio results.^28,29The obtained results are reported inTable 2. Our calculations show that S7 is the most basic centers and the relative trend of intrinsic basicity is as follow:S7> O6> S1 >N3., confirming that the isorhodanine is a sulfur base compound.Our results also suggest that the amino hydrogen atom (N3-H8) is more basic than the methylene hydrogen atom (C5-H9(10)). In comparison with similar systems, the N3-H8 bond in isorhodanineis characterized by a moderate acidity and it is sensibly lower than that of thiohydantoin²⁶ (~336-341 kcal mol^-1) and uracil²⁵ (~334-358 kcal mol^-1)²⁵.Finally, considering the solvent effect shows a drastic change in the values of PA, GBand DH_dep. This change agrees with those obtained for other systems (see Table 2)^22,29.

Table 2: Gas and solvent phase proton affinity, PA / kcal mol^-1, gas-phase basicity, GB / kcal mol^-1, and the enthalpy of deprotonation, DH_dep/ kcal mol^-1, of isorhodanine obtained at B3LYP/6.-11++(3df,2p)//B3LYP/6.-11+(d,p level of theory. 

	Gas phase			water
	PA	GB	DHdep	PA	GB	DHdep
S1	172.2	165.0	–	-43.3	-45.2	–
O6	190.1	184.6	–	-33.7	-32.5	–
N3	166.9	160.2	–	-53.3	-51.4	–
S7	194.4	187.9	–	-25.8	-22.7	–
N3-H8	–	–	324.2	–	–	554.8
C5-H2(3)	–	–	330.0	–	–	560.0

 

Intramolecular Proton transfer

The question remained in this part is: whether of the above mentioned tautomerscould be observed in the gas phase and in water? In order to answer this question the transition states of the intramolecular proton transfer (IPT) processes through 1,3-H migration have been located and characterized at the same level of theory (B3LYP/6-311++G(3df,2p)//6.311-G(d,p). It is well known that the IPT process is of great importance in many chemical and biological systems37-39. A possible mechanisms of IPT, tautomericequilibria and appropriateproperties associated with IPT processes have been studied theoretically and experimentally40-46. Of particular importance, we aim to study the IPT processes of N(H)-C=ON=C-OH , N(H)-C=SN=C-SH and C(H2)-C=SC(H)=C-SH in gas phase and in water. Table 3 reports the (B3LYP/6-311++G(3df,2p)//6.311-G(d,p) relative activation energies of IPT process in the gas phase and the solvent for all cases under probe. The corresponding figures are available from author upon request.
Our computed results show that the IPT reaction, in all cases, is characterized by high activation barriers in gas phase as well as in water.

Table 3: Relative energies, ΔE / kcal mol-1, of the intramolecular proton transfer processes of the neutral, protonated and deprotonated isorhodanine.

	IPT reaction	Gas	Water
neutral
TSN1	R1®R3	33.9	36.4
TSN2	R1®R4	50.5	52.7
TSN3	R1®R6	46.6	50.9
TSN4	R6®R8	63.0	64.1
TSN5	R4®R10	50.2	52.9
protonated
TSP1	P2b®P5a	38.0	42.0
TSP2	P1a®P3b	56.1	60.1
TSP3	P1a®P1b	14.8	15.3
TSP4	P1b®P4b	35.0	38.0
deprotonated
TSD1	D1®D3	49.5	53.2
TSD2	D2®D4	32.2	34.6

 

For neutral species as can be seen in Table 2, the reaction barrier of the transition of oxo/thione to oxo/thiol form (R1®R3) through TSN1 is equal to 33.9  kcal mol^-1 and that of  transition of oxo/thione to enol/thione form R1®R6 via TSN3 is found to be 46.6 kcal mol^-1in gas phase.

For protonated isorhodanine, the gas phase activation barriers of the IPT process of the protonated oxo/thione to enol/thione form (P2b®P5a) via TSP1 is about 38 kcal mol^-1. Whereas, the gas phase activation energy of the transition of the protonated isorhodanine to the oxo/thiol form (P1a®P1b®P4b) through TSP3 then TSP4 is about 35 kcal mol^-1 with respect to the global minimum.

For deprotonated isorhodanine, the IPT reaction (C(H2)-C=S®C(H)=C-SH (D1®D3) to form the oxo/thiol form, D3, starting from the oxo/thione form, D1,via TD1 requires a very high activation barriers of about 50 kcal mol^-1in gas phase. While, the formation of the enol/thione tautomer of D4 from the global minimum, D1, through TD2 requires about 32 kcal mol^-1 in gas phase.

In summary, our results show that the gas phase activation barriers for the IPT processes of the neutral, the protonated and the deprotonated species are very and thermodynamically unfavored. However, the same processes show a gas phase activation barriers in the case of the protonated and deprotonated species lower than those in the case of the neutral form, reflecting some possible catalytic effect of the protonation and deprotonation process on the keto-enol/thione-thiol processes. The same effects were also shown previously²⁸.

Geometrical aspects

Our results show that the 1,3-H transfer process accompanies by a significant change of the corresponding C2=O6 and C4=S7 bond lengths and the N3-C2=O6, N3-C4=S7and C5-C4=S7 bond angles. The C2=O6 and C4=S7 bonds are elongated and the N3-C2=O4 and N3-C4=S7 bond angles are decreased. Most relevant geometrical parametersof all possible structures R1-R11 are reported in Table 4.

Table 4: Selected geometrical structures, C2=O6 (B1) and C4=S7 (B2) Bond lengths / Å and N3-C2=O6 (A1), N3-C4=S7 (A2) and C5-C4=S7 (A3) Bond angles in / °of the tautomeric forms of the neutral isorhodanine, obtained at B3LYP/6-311+G(d,p) level of theory in gas phase and in solution.

	Gas					Water
	B1	B2	A1	A2	A3	B1	B2	A1	A2	A3
R1	1.198	1.642	124.6	125.3	124.3	1.205	1.650	124.3	125.0	124.2
R2	1.192	1.758	125.8	118.6	121.1	1.206	1.746	124.9	118.7	121.5
R3	1.340	1.777	124.9	120.1	123.7	1.337	1.780	125.5	120.3	123.3
R4	1.193	1.756	125.5	122.5	117.1	1.206	1.746	124.7	122.9	117.3
R5	1.205	1.772	127.4	120.5	126.2	1.217	1.771	127.3	120.7	125.8
R6	1.324	1.640	123.0	125.2	121.5	1.315	1.657	123.2	124.3	121.6
R7	1.205	1.772	127.4	120.5	126.2	1.217	1.771	127.3	120.7	125.8
R8	1.344	1.777	121.7	119.5	123.9	1.341	1.781	121.1	120.3	123.1
R9	1.328	1.640	120.5	125.4	120.8	1.318	1.658	119.0	124.4	121.3
R10	1.340	1.776	124.8	115.3	128.5	1.337	1.779	125.3	115.2	128.4
R11	1.344	1.776	121.8	115.1	128.2	1.341	1.779	121.0	115.2	128.2
MAD	–	–	–	–	–	0.064	0.048	2.0	2.7	2.5

 

Our results show a significant variation in the bond lengths and bond angles when the protonation and deprotonation processes take place. These changes are mirrored when the molecular graphs based on quantum theory of atoms in molecules (QTAIM) of Bader³⁴ have been studied. Fig. 1 shows the optimized geometrical structures and the corresponding molecular graphs based on QTAIM of Bader³⁴ of the predominant structures of the neutral (R1), protonated (P2b) and deprotonated (D1) forms of isorhodanine molecule. As can be seen, the changes in the geometries of the neutral parents system after protonation anddeprotonation processes exhibits the expected variation. For example, the C4=S7 bond becomes longer when the protonation and deprotonation processes take place. Protonation process leads to lengthening of C4=S7 bond and shortening of the adjacent bonds (N3-C2 and C4-C5). Whereas, deprotonation process leads to an enhancement in conjugation of the remaining imine group with the adjacent C2=O6 and C4=S7 groups. To confirm these results, it is found that thecharge densities at the bond critical points (BCPs) of the protonated C4=S7 bond (P2b) decreases in comparison with the neutral one (R1). Whereas those of the C2=O6 and C4=S7 bonds (D1) decrease in comparison with R1when the deprotonation of the amino group take place.

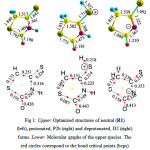Figure 1: Upper: Optimized structures of neutral (R1) (left), protonated, P2b (right) and deprotonated, D2 (right) forms. Lower: Molecular graphs of the upper species. The red circles correspond to the bond critical points (bcps) while the yellow circles correspond to the ring critical points (rcps). Click here to View Figure

 

Solvent effect on the relative stability

Ongoing from the gas phase to solution (water), the following observation have been noticed:

Relative energies

The calculated relative energies in water phase of all species under considerations are gathered in Table 1. The effect of solvent on the relative energies of the tautomeric forms are shown in Fig. 2. As can be see, introducing of the solvent does not change the relativity stability trend, but interestingly, drop the relative energy difference between the global minima in the case of the neutral species (R1 (Fig. 2a) and the deprotonated species (D1 (Fig. 2c)) and the other tautomeric forms, which leads to stabilize the tautomeric forms. Whereas, in the case of the protonated species (Fig.2b), the relative energy gaps between the global minimum (P2b) and the other protonated tautomeric forms rise, leading to destabilize the tautomeric structures. These findings can be explained by the  solvent-solute interaction. In the case of the protonated species, interaction of the heteroatoms (O6 or S7) with the incoming proton leads weakness the interaction between the solvent (water) the heteroatoms), which leads to destabilize the tautomeric forms with respect to the global minimum (see Table 1).

Figure 2: The solvent effect on the relative stability of (a) neutral (b) protonated and (c) deprotonated of isorhodaninetautomers. Click here to View Figure

 

Fig. 3 shows the activation barriers of the neutral species in both gas phase and solvent. As can be seen from the figure that the solvated activation barriers are systematically higher than those in the gas phase, which leads to destabilize the transition states in when the solvent is introduced. These findings indicate that the IPT processes are preferred in gas phase

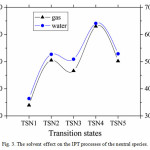Figure 3: Thesolvent effect on the IPT processes of the neutral species.  Click here to View Figure

 

Geometrical structure

It is well known that the geometry of the solute does undergo important changes on going from the gas phase to solution.The effect of medium on the molecular geometry of the isorhodanine was investigated with PCM. Our results show a significant changes in the geometrical parameters by changing the medium.The mean absolute deviations (MAD) arealso gathered in Table 4. It can be seen from Table 3 that the mean absolute deviation (MAD) of C2=O6 and C4=S7 bond lengths in water from gas phase are 0.064 and 0.048 Å, respectively whereas of N3-C2=O6, N3-C4=S7 and C5-C4=S7 bond angles they are 2.0, 2.7 and 2.5°, respectively. Interestingly, all calculated gas phase bond lengths and bond angles of the tautomer R1 are significantly shorter and larger, respectively, than those in water where intermolecular hydrogen may exist between solute and solvent

Conclusions

We have carried out a computational study on the  structure and relative stability of neutral, protonated and deprotonated isorhodaninetautomers using density functional theory at B3LY/6-311+G(d,p) level in the gas phase and in solution. The results of this work can be summarized as follow. DFT calculations predict that the oxo/thione tautomer of the thizaolidine-2-one-4-thione, in its neutral, protonated and deprotonated forms, is the most stable and predominant in both gas phase and in solution. Prototropictautomerization process would be take place at the sulfur atom rather than at the oxygen atom. Protonation at sulfur would be larger than protonation at oxygen. Deprotonation of the amino group (N-H) would be preferred than of the methylene group. The most stable protonated form of the  thiazolidin-2-one-4-thione have the incoming proton attached to the sulfur atom. Results revealed that thiazolidin-2-one-4-thione possesses moderately strong proton affinities. Although protonation and deprotonation process may play a catalytic role in lowering the activation barriers of the isomerization process, these barriers for proton migration between the different tautomers are still rather large and the process is thermodynamically not allowed. Changing of the medium has no significant effect on the relative stabilities of the different forms in all cases.

In solution, the most remarkable results were certainly the drastic change of the proton affinity and the molecular gas phase basicity on going from gas to water. So that according to the proposed solvation model, one concludes that the protonation is not energetically favorable in solution. Moreover, consideration of the solvent causes some reordering of the relative stability of isorhodanine forms in all cases.Our results also indicate that in the gas phase, all calculated C2=O6 and C4=S7 bond distances are significantly shorter than in water where solute-solvent interactions (hydrogen bonds) are present and fell in the range 0.064-0.048Å. All calculated bond angles (containing N, O and S) in the gas phase are significantly smaller than in those in water and fell in the range 2.0-2.7°.

Acknowledgment

A generous allocation of computational time at the Scientific Computational Center (CCC) of the Universidad Autónoma de Madrid (Spain) is acknowledged.

References

1. Pozharskii A. F.; Soldatenkov A.T.; Katrizky A. R.; Heterocyclic in Life and society, Wiley, New York, 1997.
2. Ludlow J. W.; Guikema J. A.; Consigli R. A., Anal. Biochem.,1986, 154, 104-109.
3. Raper E.S., Coord. Chem. Rev., 1985, 61, 115-184.
4. Majidi M. R.; Asadpour-Zeynali K.; Hosseini S.-A., Electroanalysis, 2007, 19, 364-369.
5. Tamasabhi D., J. Mol. Struct. (Theochem), 2003, 638, 11-20.
6. Enchev V.; Chorbadjiev S.; Jordanov B.; Chemistry of heterocyclic compounds, 2002, 38, 1110-1120.
7. Andreocci M. V.; Cauletti C.; Sestili L., Spectrochim. Acta A, 1984,40, 1087-1096.
8. Al-Sehemi A. G.; El-Gogary T. M., J. Mol. Struct. (THEOCHEM),2008,907, 66-73.
9. Raczynska E.D.; Kosinska W.; Osmialowski B.; Gawinecki R.; Chem. Rev., 2005, 105, 3561-3612.
10. Stewart R., in The Proton: Appellation to Organic Chemistry, Academic Press, NewYork, 1985.
11. Carrol F.A., Perspectives on structure and mechanism in organic chemistry, Brooks-Cole, New York, 1998.
12. Uggerud E., Mass Spectrom. Rev., 1992, 11,389-430.
13. Chandra A. K. ; Goursot A., J. Phys. Chem., 1996,100, 11596-11599.
14. Rao J. S.;  Sastry G. N.; Int. J. of Quantum Chemistry, 2006, 106, 1217-1224.
15. Mautner M. M.-N., J. Am. Chem. Soc.,1988, 110, 3071-3075.
16. Berthelot M.; Decouzon M.; Gal J.F., Laurence C.; Le Questel Y. J;  Maria P.-C.;Tortajada J., J. Org. Chem.,1991, 56, 4490-4494.
17. Szulejko J. E.; McMahon T. B., J. Am. Chem. Soc., 1993, 115, 7839-7848.
18. Wieczorek R.; Dannenberg J. J., J. Am. Chem. Soc.,2004, 126, 12278-12279.
19. Van Beelen S. E.; Koblenz T. A.; Ingemann S.; Hammmerum S., J. Phys. Chem. A, 2004, 108, 2787-2793..
20. Lamsabhi M.; Alcamí M.; Mo O.; Bouab W.; Esseffar M.; Abboud J. L.M..; Yāñez M., J. Phys. Chem. A, 2000,104, 5122-5130.
21. Abboud J. L.-M.; Mo O.; de Paz J. L. G.; Yāñez M.; Esseffar M.; Bouab W.; El-Mouhtadi M.; Mokhlisse R.; Ballesteros E.; Herreros M.; Homan H.; Lopez-Mardomingo C.; Notario R., J. Am. Chem. Soc., 1993, 115, 12468-12476.
22. Lamsabhi M.; Esseffar M.; Bouab W.; El Messaoudi T.; El Messaoudi M.; Abboud J. L.-M.; Alcamí M.; Yāñez M., J. Phys. Chem. A, 2002, 106, 7383-7389.
23. Mo O.; De Paz J. L. G.; Yāñez M., J. Phys. Chem. A, 1987, 91, 6484-6490.
24. Dang P.; Madan A. K., J. Chem. Inf. Comput. Sci., 1994, 34, 1162-1166.
25. Locock R. A.; Coutts R. T., Org. Mass Spectrom.,1970, 3(6), 735-745.
26. Nguyen M. T.; Chandra A. K.; Zeegers-Huyskens T., J. Chem. Soc.Faraday Trans.,1998, 94(9), 1277-1287.
27. Safi Z., Eurpoean Journal of Chemistry, 2012,3,343-348.
28. Safi Z.; Frenking G., Int. J. of Quantum. Chem.,2013,113 (7),  908-915.
29. Safi Z.; Omar S., Chem. Phys. Lett.2014, 610–611, 321-330.
30. M. J. Frisch, et al Gaussian 09; Gaussian, Inc., Pittsburgh, PA, 2009.
31. Becke A. D., J. Chem. Phys.,1993, 98, 5648-56452.
32. Lee C.; Yang W.; Parr R. G., Phys. Rev. B, 1988, 37, 785-789.
33. Scott A. P.; Radom L., J. Phys. Chem. 1996, 100, 16502-19513.
34. Bader R. F. W, in  Atoms in Molecules: A Quantum Theory, Clarendon Press Oxford Univ.: Oxford, 1990.
35. Biegler-König F.; Schönbohm J., J. Comp. Chem., 2002, 23, 1489-1494.
36. Pappalardo R. R.; Marcos E. S.; Ruiz-López M. F., J. Am. Chem. Soc.,1993, 11, 3722-3811.
37. Madeja F.; HavenithM.,J. Chem. Phys.,2002, 117, 7162-7168.
38. Alavi S.; Thomson L.D.,J. Chem. Phys., 2002, 117, 2599-2602.
39. Bell R.L.; Truong, T.N.,J. Chem. Phys.1994, 101, 10442-10451.
40. Zhanpeisov N.U.; Cox W.W.,J. Phys. Chem. A,1999,103, 4564-4571.
41. Shukla M.K.; Leszczynski J.,J. Phys. Chem. A,2000,104, 3021-3027.
42. Gorb L.; Podolyan Y.; Leszczynski J.; Siebrand W.; Ferna´ndez-Ramos A.; Smedarchina Z., Biopolymers, 2002, 61, 77-83.
43. Taylor J.; Eliezer I.; Sevilla M.D.,J. Phys. Chem. B,2001, 105, 1614-1617.
44. Cui Q.; Karplus M.,J. Phys. Chem. B,2003, 107, 1071-1078.
45. Kulhanek P.; Schlag, E.W.; Koca, J.,J. Am. Chem. Soc.2003, 125, 13678-13679.
46. Li P. ; Bu Y.X., J. Phys. Chem. A, 2004, 108, 1028-1036.

 

---

This work is licensed under a Creative Commons Attribution 4.0 International License.