Optimisation of Arsenic (III) by Colorimetric Incorporated with Image Processing Technique

Introduction

Inorganic arsenic contamination has caused a remarkable impact on the contamination of soil and groundwater in many countries of the world¹. Arsenic occurs in nature water in various forms of inorganic and organic² and mainly found in two inorganic forms i.e. As³⁺ and As⁵⁺, whereby As (III) is more toxic than As (V)³. According to Shen et. al (2013)⁴, As (III) is able to bind to a specific protein which could alter the protein’s conformation, leading to a deterioration in cellular functions. In addition, based on the report by Bednar et al. (2004)⁵ determination of each inorganic arsenic species is crucial due to the extensive variation in the toxicology, mobility, and absorptivity of each species.

Although laboratory analysis provides a highly accuracy and precision technique to measure arsenic in water samples, however due to time and cost constraints. Various test kit have been developed based on colorimetric method, but the results is normally based on comparison of the color formed on the test strip with a reference color scale which is rather subjective and operator-dependent. Thus there is a need for improvement for in-situ analysis of arsenic. According to Wang et al. (2011)⁶, an ideal field deployable sensor would be able to detect low µg/L concentration of analyte directly on-site with little or no sample preparation as well as persistence to interference ions. In fact, colorimetric methods can provide results nearly as accurate and reliable as those from analytical laboratories when the reaction is automatically evaluated by means of a color detector⁷. An electronic device for measuring color has been introduced to minimize human error in interpreting the color with naked eyes for determination of arsenic. For example, Anderson et al. (2008)⁸ measured reflectance of the developed color spot and convert it to digital signal by an electronic transducer which requires 30 to 40 minutes to detect of arsenic.

Thus, a more rapid, simple and ecofriendly approach was developed in this study to determine arsenic (III) by incorporation of image processing technique into colorimetric method. The effects of different factors were investigated by a 2⁴ full factorial design with a blocking factor. The effects consists of weight load used for drying silver nitrate-impregnated filter paper, drying period of silver nitrate-impregnated filter paper, mass ratio of sulfamic acid to zinc powder and reaction period between arsine gas generated and silver nitrate which were evaluated at two levels to determine the significant factors before optimize the detection of arsenic (III).

Materials and Methods

Reagents and Materials

Arsenic (III) stock solution containing 1,000 mg As (III)/L (Merck, Germany) was used to prepare As (III) working standard solutions. Sulfamic acid, silver nitrate and zinc powder were also obtained from Merck (Germany). All the chemicals used in this study were of analytical grade.

Preparation of As (III) working standard solutions

As (III) working standard solutions containing 0 to 300 µg/L of As (III) were freshly prepared from the As (III) stock solution by proper dilutions using ultrapure water.

Preparation of 5% (w/v) silver nitrate solution

A 5% solution of silver nitrate was prepared by dissolving the silver nitrate using ultrapure water in a 100 mL volumetric flask.

Preparation of silver nitrate-impregnated filter paper

Whatman filter paper No.3 was cut into a 2.5 cm (diameter) round-shaped piece of the paper. It was then dipped into the silver nitrate solution for period of 2 seconds and followed by drying it between two pieces of dry Whatman filter papers which was pressed using a 100 or 500 g load for 20 or 60 seconds. This silver nitrate-impregnated filter paper was used as arsine sensor paper.

Colored complex formation

Minitab software (version 17.0) (USA) was utilized to randomize the ninety-six experimental runs with all possible combinations of factors in duplicates at high and low levels to investigate the effect of weight load (100 or 500 g) used for drying silver nitrate-impregnated filter paper (DW), drying period of silver nitrate-impregnated filter paper (DP) (20 or 60 s), mass ratio of sulfamic acid to zinc powder (MSZ) (1.0 g: 0.5 g or 4.0 g: 2.0 g), and reaction period (RP) (5 or 10 minutes).

Table 1: Low and High Levels of Factors

Factor	Low level (-1)	High level (+1)
Weight load used for drying silver nitrate-impregnated filter paper (DW)(X1), g	100	500
Reaction period (RP)(X4), min.	5	10
Mass ratio sulfamic acid to zinc powder (MSZ)(X3)	1:0.5	4:2
Drying period of silver nitrate-impregnated filter paper (DP)(X2), s	20	60

A 60 mL of polypropylene bottle was filled with 50 mL of arsenic (III) working standard solution. To the solution, desired amount of sulfamic acid was added and swirled before adding zinc powder and swirled again to ensure homogeneity of the mixture.  The arsine sensor paper was then inserted inside the cap of the bottle before close the bottle with cap. The bottle was swirled gently before stand for the selected reaction period.  Each experiment was performed in duplicates at 25 ºC and at the levels as presented in Table 1. As soon as the reaction period was over, the colored arsine sensor paper was removed from the cap and used for image analysis.

Color image processing

For each colored arsine sensor paper, two images were captured by a digital camera (Sony Cyber-shot, DSC-W610) at the distance of 15 cm. All conditions including distance, lighting conditions (automatic mode) and camera setting were kept constant for all experiments. The color (red, green and blue) of the images were transformed into digital readings from 0 to 225 using Image J software and used for further statistical analysis.

Statistical Analysis

To determine significant factors, Analysis of Variance (ANOVA), Student’s t-analysis, correlation between response variables, linear regression analysis were carried out. Main and interaction effects plots were also formed for each color value. All these data analysis was performed using Minitab software (version 17.0) (USA). Besides that, normal probability and residual versus fitted value plots were also formed using the software.

Optimisation of detection

Optimisation plot was constructed to suggest the optimum conditions of arsenic (III) detection using the Minitab software. Validation of the suggested optimum conditions was performed by conducting the detection experiments at the suggested conditions in 5 replications. The experiments was carried out similar to the procedure as mentioned in the section of Colored complex formation at the suggested optimum conditions.

Data Analysis

To determine the significant factors that affect the detection of arsenic (III), all data analysis including linear regression analysis, Analysis of Variance (ANOVA), Student’s t-analysis and correlation between response variables were implemented using the Minitab software version 17.0 (Minitab Inc., PA, USA). Main effects plot was also developed for each color value for significant contribution factors.

Results and Discussion

Colorimetric method used in this work was based on modification of the methods developed by Cherukuri and Anjaneyulu (2005)⁹ and later by Ong et al. (2015)¹⁰.

Table 2: Experimental results for detection of arsenic (III)

DW (g)	DP (s)	MSZ	RP (min)	Arsenic (III) Concentration (µg/L)	Color value			Std Order	Run Order	Center Pt
					Red	Green	Blue
100	20	1	5	0	134.929	153.018	147.315	1	1	1
100	20	1	5	10	133.998	151.394	145.087	2	2	1
100	20	1	5	50	132.183	149.634	141.730	3	3	1
100	20	1	5	100	114.965	117.107	83.968	4	4	1
100	20	1	5	200	81.996	75.166	37.681	5	5	1
100	20	1	5	300	69.744	60.594	29.444	6	6	1
100	20	4	5	0	130.952	149.481	141.914	7	7	1
100	20	4	5	10	129.994	148.549	139.079	8	8	1
100	20	4	5	50	128.233	142.955	119.901	9	9	1
100	20	4	5	100	109.984	107.052	54.206	10	10	1
100	20	4	5	200	76.035	66.674	39.770	11	11	1
100	20	4	5	300	62.758	54.816	25.165	12	12	1
100	20	1	10	0	127.595	146.614	140.348	13	13	1
100	20	1	10	10	126.131	143.815	136.440	14	14	1
100	20	1	10	50	124.349	139.430	125.608	15	15	1
100	20	1	10	100	94.167	90.073	46.823	16	16	1
100	20	1	10	200	66.920	57.250	27.520	17	17	1
100	20	1	10	300	55.009	47.087	26.081	18	18	1
100	20	4	10	0	127.838	145.430	139.492	19	19	1
100	20	4	10	10	124.303	140.702	130.960	20	20	1
100	20	4	10	50	116.619	127.183	88.124	21	21	1
100	20	4	10	100	81.522	79.398	31.002	22	22	1
100	20	4	10	200	63.480	56.726	23.869	23	23	1
100	20	4	10	300	45.391	43.210	22.024	24	24	1
100	60	1	5	0	136.792	153.882	147.563	25	25	1
100	60	1	5	10	132.738	149.684	140.869	26	26	1
100	60	1	5	50	129.333	142.622	127.591	27	27	1
100	60	1	5	100	120.250	130.602	104.074	28	28	1
100	60	1	5	200	112.361	111.685	71.303	29	29	1
100	60	1	5	300	106.105	100.668	51.942	30	30	1
100	60	4	5	0	127.069	144.288	133.833	31	31	1
100	60	4	5	10	126.768	143.310	131.752	32	32	1
100	60	4	5	50	128.274	144.533	127.201	33	33	1
100	60	4	5	100	111.125	115.634	66.637	34	34	1
100	60	4	5	200	92.451	81.186	44.570	35	35	1
100	60	4	5	300	71.154	59.406	30.447	36	36	1
100	60	1	10	0	133.098	152.654	148.877	37	37	1
100	60	1	10	10	126.638	145.583	142.822	38	38	1
100	60	1	10	50	112.648	129.302	127.987	39	39	1
100	60	1	10	100	95.679	89.897	45.293	40	40	1
100	60	1	10	200	63.582	55.871	24.001	41	41	1
100	60	1	10	300	49.367	42.740	22.007	42	42	1
100	60	4	10	0	122.400	139.719	133.587	43	43	1
100	60	4	10	10	127.090	143.890	135.080	44	44	1
100	60	4	10	50	121.196	130.382	89.783	45	45	1
100	60	4	10	100	84.055	82.267	28.763	46	46	1
100	60	4	10	200	68.112	62.123	21.130	47	47	1
100	60	4	10	300	54.150	47.651	21.993	48	48	1
500	60	1	10	0	136.793	155.491	152.644	49	49	1
500	60	1	10	10	131.622	149.281	146.564	50	50	1
500	60	1	10	50	135.405	151.637	146.537	51	51	1
500	60	1	10	100	114.595	121.003	93.401	52	52	1
500	60	1	10	200	104.155	98.945	52.794	53	53	1
500	60	1	10	300	94.655	86.561	43.278	54	54	1
500	60	1	5	0	133.138	149.563	141.373	55	55	1
500	60	1	5	10	132.178	148.875	140.904	56	56	1
500	60	1	5	50	125.615	139.866	117.701	57	57	1
500	60	1	5	100	113.730	115.078	64.876	58	58	1
500	60	1	5	200	101.051	94.947	39.514	59	59	1
500	60	1	5	300	83.001	73.410	26.479	60	60	1
500	20	1	5	0	128.106	145.621	139.839	61	61	1
500	20	1	5	10	130.079	147.265	140.111	62	62	1
500	20	1	5	50	130.201	145.643	129.774	63	63	1
500	20	1	5	100	102.316	102.132	63.249	64	64	1
500	20	1	5	200	70.654	61.166	29.168	65	65	1
500	20	1	5	300	59.520	50.683	24.021	66	66	1
500	20	4	5	0	131.697	150.428	147.854	67	67	1
500	20	4	5	10	125.379	141.680	131.462	68	68	1
500	20	4	5	50	96.648	106.171	70.494	69	69	1
500	20	4	5	100	76.423	71.536	25.635	70	70	1
500	20	4	5	200	49.939	45.328	22.642	71	71	1
500	20	4	5	300	46.059	42.446	25.182	72	72	1
500	20	1	10	0	130.418	148.622	145.224	73	73	1
500	20	1	10	10	131.638	148.659	144.986	74	74	1
500	20	1	10	50	126.705	143.390	138.145	75	75	1
500	20	1	10	100	119.817	124.719	91.182	76	76	1
500	20	1	10	200	90.857	88.574	55.037	77	77	1
500	20	1	10	300	78.105	70.236	32.173	78	78	1
500	20	4	10	0	128.167	144.262	137.551	79	79	1
500	20	4	10	10	129.817	146.586	140.104	80	80	1
500	20	4	10	50	123.058	136.867	119.304	81	81	1
500	20	4	10	100	114.697	115.249	65.165	82	82	1
500	20	4	10	200	89.996	81.248	30.444	83	83	1
500	20	4	10	300	72.356	60.805	23.572	84	84	1
500	60	4	5	0	135.358	153.436	148.180	85	85	1
500	60	4	5	10	131.337	149.016	143.035	86	86	1
500	60	4	5	50	127.215	142.622	128.297	87	87	1
500	60	4	5	100	109.072	108.769	62.776	88	88	1
500	60	4	5	200	82.429	69.917	27.049	89	89	1
500	60	4	5	300	56.139	48.689	21.712	90	90	1
500	60	4	10	0	132.673	150.651	143.491	91	91	1
500	60	4	10	10	116.933	131.173	112.984	92	92	1
500	60	4	10	50	121.582	124.256	70.959	93	93	1
500	60	4	10	100	83.550	74.764	26.496	94	94	1
500	60	4	10	200	66.479	55.596	19.859	95	95	1
500	60	4	10	300	47.531	41.547	21.623	96	96	1

 

Red, green and blue (RGB) color values are the responses in this work which produced by a change in the level of a factor.  The regression analysis of red, green and blue color values are displayed in Table 3, 4 and 5, respectively. The results revealed that the main effects of mass ratio of sulfamic acid to zinc powder (MSZ) and reaction period (RP) were significant at a 5% of probability level (p < 0.05) for all color values. However, for interaction effect, drying weight-drying period of silver nitrate-impregnated filter-paper-reaction period (DW x DP x RP) interaction and drying weight-mass ratio of sulfamic acid to zinc powder -reaction period (DW x MSZ x RP) interaction were significant at a 5% of probability level (p < 0.05) for red and green. However, such interaction effects do not exist in blue color.

Table 3: Statistical Parameters for 2⁴ full factorial design of red color value

Term	Effects	Coefficients	Standard Error	T-value	P-value
Constant	–	103.04	1.21	122.11	0.000
DW	1.820	0.910	0.862	1.06	0.295
DP	1.798	0.899	0.862	1.04	0.301
MSZ	-7.607	-3.803	0.862	-4.41	0.000
RP	-16.106	-8.053	0.862	-9.34	0.000
DW x DP	-2.091	-1.046	0.862	-1.21	0.229
DW x MSZ	0.232	0.116	0.862	-0.80	0.429
DW x RP	0.096	0.048	0.862	0.06	0.956
DP x MSZ	0.232	0.116	0.862	-0.80	0.429
DP x RP	1.034	0.517	0.862	0.60	0.551
MSZ x RP	-1.000	-0.500	0.862	-0.58	0.564
DW x DP x MSZ	1.060	0.530	0.862	0.61	0.541
DW x DP x RP	4.532	2.266	0.862	2.63	0.010
DW x MSZ x RP	-3.982	-1.991	0.862	-2.31	0.024
DP x MSZ x RP	1.974	0.987	0.862	1.14	0.256
DW x DP x MSZ x RP	-1.438	-0.719	0.862	-0.83	0.407

 

Table 4: Statistical Parameters for 2⁴ full factorial design of green color value

Term	Effects	Coefficients	Standard Error	T-value	P-value
Constant	–	110.910	0.950	116.73	0.000
DW	1.281	0.640	0.950	0.67	0.502
DP	1.482	0.741	0.950	0.78	0.438
MSZ	-9.366	-4.683	0.950	-4.93	0.000
RP	-17.673	-8.836	0.950	-9.30	0.000
DW x DP	-2.944	-1.472	0.950	-1.55	0.125
DW x MSZ	-1.874	-0.937	0.950	-0.99	0.327
DW x RP	-0.383	-0.192	0.950	-0.20	0.841
DP x MSZ	-0.820	-0.410	0.950	-0.43	0.668
DP x RP	0.414	0.207	0.950	0.22	0.828
MSZ x RP	-0.260	-0.130	0.950	-0.14	0.892
DW x DP x MSZ	0.922	0.461	0.950	0.49	0.629
DW x DP x RP	4.410	2.205	0.950	2.32	0.023
DW x MSZ x RP	-4.283	-2.141	0.950	-2.25	0.027
DP x MSZ x RP	1.739	0.869	0.950	0.92	0.363
DW x DP x MSZ x RP	-1.803	-0.902	0.950	-0.95	0.346

Table 5: Statistical Parameters for 2⁴ full factorial design of blue color value

Term	Effects	Coefficients	Standard Error	T-value	P-value
Constant		86.74	1.18	73.81	0.000
DW	0.05	0.02	1.18	0.02	0.985
DP	0.20	0.10	1.18	0.08	0.934
MSZ	-15.74	-7.87	1.18	-6.70	0.000
RP	-17.01	-8.51	1.18	-7.24	0.000
DW x DP	-2.95	-1.48	1.18	-1.26	0.213
DW x MSZ	-2.32	-1.16	1.18	-0.99	0.327
DW x RP	-0.20	-0.10	1.18	-0.09	0.932
DP x MSZ	-1.58	-0.79	1.18	-0.67	0.503
DP x RP	-1.03	-0.51	1.18	-0.44	0.664
MSZ x RP	-0.36	-0.18	1.18	-0.15	0.877
DW x DP x MSZ	0.79	0.40	1.18	0.34	0.737
DW x DP x RP	1.87	0.93	1.18	0.80	0.429
DW x MSZ x RP	-1.45	-0.73	1.18	-0.62	0.539
DP x MSZ x RP	-0.34	-0.17	1.18	-0.14	0.887
DW x DP x MSZ x RP	-1.60	-0.80	1.18	-0.68	0.498

Equations 1, 2 and 3 indicate the models that relate the levels of parameter and red, green and blue color values, respectively.

Red color value

103.04 + 0.910X₁ + 0.899X₂ -3.803X₃ -8.053X₄ – 1.046X₁X₂ + 0.116X₁X₃ + 0.048X₁X₄ +0.116X₂X₃ + 0.517X₂X₄-0.500X₃X₄ + 0.530X₁X₂X₃ + 2.266X₁X₂X₄ -1.991X₁X₃X₄ + 0.987X₂X₃X₄ -0.719 X₁X₂X₃X₄                                                           (1)     

Green color value

110.910 +0.640X₁ + 0.741X₂ -4.683X₃ -8.836X₄ – 1.472X₁X₂ – 0.937X₁X₃ -0.192X₁X₄ – 0.140X₂X₃ + 0.207X₂X₄ -0.130 X₃X₄ + 0.461X₁X₂X₃ + 2.205X₁X₂X₄ -2.141X₁X₃X₄ +0.869 X₂X₃X₄ -0.902 X₁X₂X₃X₄                                                           (2)                                                            

Blue color value

86.74 + 0.02X₁ + 0.10X₂ -7.87X₃ -8.51X₄ – 1.48X₁X₂ – 1.16X₁X₃ -0.10X₁X₄ – 0.79X₂X₃– 0.51X₂X₄-0.18X₃X₄ + 0.40X₁X₂X₃ + 0.93X₁X₂X₄ -0.73X₁X₃X₄ -0.17X₂X₃X₄ -0.80X₁X₂X₃X₄                                                                                                                                           (3)                                                                                                                                                                                                   

 A factor that positively significant can be seen from the color value decreases as the change from low to high level or vice versa, while if the colors are red, green and blue formed a high level of the same factors, it is negative effect. Figures 1, 2 and 3 illustrate the main effects of the factors for red, green and blue color values.

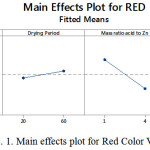Figure 1: Main effects plot for Red Color Value   Click here to View Figure

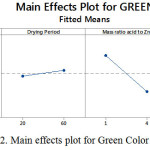Figure 2: Main effects plot for Green Color Value   Click here to View Figure

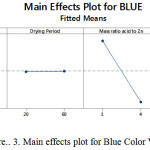Figure 3: Main effects plot for Blue Color Value   Click here to View Figure

 

Tables 6, 7 and 8 show the results of Analysis of Variance for three response colors, respectively. The sum of squares used to estimate the factors’ effects and F-ratios are also presented in the tables. The results revealed that the main effects of MSZ and RP are highly significant (at 5% level of significance). However, the MSZ and RP interaction are not significant and most of the interaction effects are insignificant as compared to other effects accepts for DW x DP x RP and DW x MSZ x RP. Therefore, recalculation of regression coefficients, standard error, t and p-values were conducted and the results are shown in Tables 9, 10 and 11 for red, green and blue color values, respectively.

In equations 4, 5 and 6, respectively, shows a reduced model equation with resultant coefficients for red, green and blue color values.

Red color value           = 103.04 -3.803X₃ -8.053X₄ + 2.266X₁X₂X₄ -1.991X₁X₃X₄               (4)

Green color value        = 110.910 – 4.683X₃ -8.836X₄ + 2.205X₁X₂X₄ -2.141X₁X₃X₄           (5)

Blue color value          = 86.74 -7.87X₃ -8.51X₄                                                                                (6)

Table 6: Analysis of Variance (ANOVA) for red color value

Term	Degrees of Freedom	Sum of Squares (SS)	Mean Square (MS)	F-value	P-value
BLOCKS	6	–	–	–	–
DW	1	79.5	79.5	1.11	0.295
DP	1	77.6	77.6	1.09	0.301
MSZ	1	1388.6	1388.6	19.45	0.000
RP	1	6226.0	6226.0	87.18	0.000
DW x DP	1	104.9	104.9	1.47	0.229
DW x MSZ	1	45.2	45.2	0.63	0.429
DW x RP	1	0.2	0.2	0.00	0.956
DP x MSZ	1	1.3	1.3	0.02	0.894
DP x RP	1	25.7	25.7	0.36	0.551
MSZ x RP	1	24.0	24.0	0.34	0.564
DW x DP x MSZ	1	26.9	26.9	0.38	0.541
DW x DP x RP	1	492.9	492.9	6.90	0.010
DW x MSZ x RP	1	380.5	380.5	5.33	0.024
DP x MSZ x RP	1	93.5	93.5	1.31	0.256
DW x DT x MSZ x RP	1	49.6	49.6	0.69	0.407
Error	75	5355.9	71.4	–	–
Total	96	74467.4	–	–	–

S = 8.45055      R-sq = 92.81%     R-sq(adj) = 90.89%

Table 7: Analysis of Variance (ANOVA) for green color value

Term	Degrees of Freedom	Sum of Squares (SS)	Mean Square (MS)	F-value	P-value
BLOCKS	6	–	–	–	–
DW	1	39	39.4	0.45	0.502
DP	1	53	52.7	0.61	0.438
MSZ	1	2105	2105.2	24.29	0.000
RP	1	7496	7495.7	86.49	0.000
DW x DP	1	208	208.1	2.40	0.125
DW x MSZ	1	84	84.3	0.97	0.327
DW x RP	1	4	3.5	0.04	0.841
DP x MSZ	1	16	16.1	0.19	0.668
DP x RP	1	4	4.1	0.05	0.828
MSZ x RP	1	2	1.6	0.02	0.892
DW x DP x MSZ	1	20	20.4	0.24	0.629
DW x DP x RP	1	467	466.7	5.39	0.023
DW x MSZ x RP	1	440	440.2	5.08	0.027
DP x MSZ x RP	1	73	72.6	0.84	0.363
DW x DP x MSZ x RP	1	78	78.0	0.90	0.346
Error	75	6500	86.7	–	–
Total	96	140097	–	–	–

S = 9.30933   R-sq = 95.36%  R-sq(adj)  = 94.12%    

Table 8: Analysis of Variance (ANOVA) for blue color value

Term	Degrees of Freedom	Sum of Squares (SS)	Mean Square (MS)	F-value	P-value
BLOCKS	6	–	–	–	–
DW	1	0	0.1	0.00	0.985
DP	1	1	0.9	0.01	0.934
MSZ	1	5947	5947.2	44.85	0.000
RP	1	6944	6944.2	52.37	0.000
DW x DP	1	209	209.2	1.58	0.213
DW x MSZ	1	129	129.3	0.98	0.327
DW x RP	1	1	1.0	0.01	0.932
DT x MSZ	1	60	60.2	0.45	0.503
DT x RP	1	25	25.3	0.19	0.664
MSZ x RP	1	3	3.2	0.02	0.877
DW x DP x MSZ	1	15	15.1	0.11	0.737
DW x DP x RP	1	84	83.8	0.63	0.429
DW x MSZ x RP	1	51	50.5	0.38	0.539
DP x MSZ x RP	1	3	2.7	0.02	0.887
DW x DP x MSZ x RP	1	62	61.6	0.46	0.498
Error	75	9946	132.6	–	–
Total	96	239449	–	–	–

S = 11.5157  R-sq = 95.85%  R-sq(adj) = 94.74%    

Table 9: Statistical parameters for 2⁴ full factorial design of red color value for reduced model

Term	Effects	Coefficients	Standard Error	T-value	P-value
Constant	–	103.04	0.844	124.75	0.000
MSZ	-7.607	-3.803	0.844	4.50	0.000
RP	-16.106	-8.053	0.844	-9.54	0.000
DW x DP x RP	4.532	2.266	0.844	2.68	0.009
DW x MSZ x RP	-3.982	-1.991	0.844	-2.36	0.021

 

Table 10: Statistical parameters for 2⁴ full factorial design of green color value for reduced

Term	Effects	Coefficients	Standard Error	T-value	P-value
Constant	–	110.910	0.926	119.76	0.000
MSZ	-9.366	-4.683	0.926	-5.06	0.000
RP	-17.673	-8.836	0.926	-9.54	0.000
DW x DP x RP	4.410	2.205	0.926	2.38	0.019
DW x MSZ x RP	-4.283	-2.141	0.926	-2.31	0.023

 

Table 11: Statistical parameters for 2⁴ full factorial design of blue color value for reduced

Term	Effects	Coefficients	Standard Error	T-value	P-value
Constant		86.74	1.12	77.48	0.000
MSZ	-15.74	-7.87	1.12	-7.03	0.000
RP	-17.01	-8.51	1.12	-7.60	0.000

Table 12, 13 and 14 illustrate the output following the removal of the insignificant main effects and interactions. The results of ANOVA for reduced models of red, green and blue color values are shown in Table 12, 13 and 14, respectively. From the results, we have sufficient evidence to conclude that reaction period (RP) was the strongest effect of the overall contributed to the three color intensities. The reduced model now contains only the main effects MSZ, RP and the DW x DP x RP and DW x MSZ x RP interactions. The X₄ coefficient was found to be the largest negative coefficient for the three models (5), (6) and (7), showing that the longer the reaction period, three color values decreased accordingly. The mass ratio of sulfamic acid to zinc powder (MSZ) was the second important factor. Third and fourth significant factors which significantly contributed for red and green color values were drying weight-drying period of silver nitrate-impregnated filter-paper-reaction period (DW x DP x RP) interaction and drying weight-mass ratio of sulfamic acid to zinc powder -reaction period (DW x MSZ x RP) interaction, respectively.

Table 12: Analysis of Variance (ANOVA) of Red Color Value for reduced model

Term	Degrees of Freedom	Sum of Squares (SS)	Mean Square (MS)	F	P
BLOCKS	6	–	–	–	–
MSZ	1	1388.6	1388.6	20.29	0.000
RP	1	6226.0	6226.0	90.99	0.000
DW x DP x RP	1	492.9	492.9	7.20	0.009
DW x MSZ x RP	1	380.5	380.5	5.56	0.021
Error	87	5884.3	68.4	–	–

S = 8.27180 R-sq = 92.10%   R-sq(adj) = 91.27%     

 

Table 13: Analysis of Variance (ANOVA) of Green Color Value for reduced model

Term	Degrees of Freedom	Sum of Squares (SS)	Mean Square (MS)	F	P
BLOCKS	6	–	–	–	–
MSZ	1	2105	2105.2	25.57	0.000
RP	1	7496	7495.7	91.04	0.000
DW x DP x RP	1	467	466.7	5.67	0.019
DW x MSZ x RP	1	440	440.2	5.35	0.023
Error	87	7081	82.3	–	–

S = 9.07367 R-sq = 94.95%   R-sq(adj) = 94.42%     

 

Table 14: Analysis of Variance (ANOVA) of Blue Color Value for reduced model

Term	Degrees of Freedom	Sum of Squares (SS)	Mean Square (MS)	F	P
BLOCKS	6	–	–	–	–
MSZ	1	5947	5947.2	49.43	0.000
RP	1	6944	6944.2	57.71	0.000
Error	88	10589	120.3	–	–
Total	96	239449	–	–	–
BLOCKS	6	–	–	–	–

S = 10.9693   R-sq = 95.58%   R-sq(adj) = 95.23%  

Figures 4, 5 and 6 present the interaction effects of red, green and blue color values, respectively. It is evident that, the effects of both MSZ and RP were more observable at high levels for all color as shown in the interaction plots of Figures 4, 5 and 6.

Figure 4: Interaction effects of reduced model for Red Color Value Click here to View Figure

Figure 5: Interaction effects for Green Color Value   Click here to View Figure

Figure 6: Interaction effects for Blue Color Value   Click here to View Figure

 

Normal distribution plot

The estimate values for all response colors showed that the experimental data are normally distributed as the experimental points were reasonably aligned, as shown in Figures 7, 8 and 9 of the normal probability plots of residual values. The residual plots showed outliers are occurred (Fig. 10, 11 and 12). However, the results showed that there were no outlier between the ranges of +25 to -15 for red color value while the ranges for green and blue color values are between +25 to – 20 and +25 to -30 respectively.

Figure 7: Normal probability plot of residual values for red color value   Click here to View Figure

Figure 8: Normal probability plot of residual values for green color value Click here to View Figure

Figure 9: Normal probability plot of residual values for blue color value Click here to View Figure

Figure 10: Residual versus fitted value plot for red color value   Click here to View Figure

Figure 11: Residual versus fitted value plot for green color value   Click here to View Figure

Figure 12: Residual versus fitted value plot for red color value   Click here to View Figure

 

Main effect of reaction period

Figures 1 to 3 show that red, green and blue values decreased by 15.79%, 14.29% and 17.89%, respectively, when the reaction period increased from 5 minutes to 10 minutes. The results from Tables 9 to 11 also exhibited that the reaction period also plays a significant role on color values. This can be explained by the fact that more arsenic (III) is reduced to arsine gas which will react with silver ions and produce darker color compound on the impregnated filter paper when longer reaction period was used.

 Main effect of mass ratio of sulfamic acid to zinc powder

As it can be seen from Figures 4 to 6, the mass ratio of sulfamic acid to zinc powder is the most significant factor as indicated by an increase in the mass ratio of sulfamic acid to zinc powder from 1 g: 0.5 g to 4 g: 2 g, caused decrease in the RGB values with the highest decrease in color values of 17.02%, 7.83%, 6.42%, for blue, green and red color values, respectively, as shown in Figures 1 to 3. This is due to the formation of darker color complex on the silver nitrate impregnated filter paper when higher mass ratio of sulfamic acid to zinc powder was applied which resulted in more production of arsine gas which reacts with silver nitrate on the impregnated filter paper. Thus, it can be said that the effect of mass ratio of sulfamic acid to zinc powder is negative in color values, but it is positive effect in detection of arsenic (III) as darker color has lower color value. Interaction effect of drying weight-drying period of silver nitrate-impregnated filter- paper-reaction period (DW x DP x RP) interaction and drying weight-mass ratio of sulfamic acid to zinc powder -reaction period (DW x MSZ x RP) interaction. Apart from main effect, interaction effects between the parameters were also investigated in this study and results are presented in Figures 7 to 9. Among all the interaction effects, there were only two of the three interaction effects i.e. drying weight-drying period of silver nitrate-impregnated filter- paper-reaction period (DW x DP x RP) interaction and drying weight-mass ratio of sulfamic acid to zinc powder-reaction period (DW x MSZ x RP) interaction were significantly affect all color values except blue color value on the production of color compunds on the silver nitrate-impregnated filter paper.

Optimisation of Arsenic (III) Detection

Experiments with various mass ratio of sulfamic acid to zinc powder (MSZ) i.e. 1.0 g: 0.5 g; 2.5 g: 1.25 g and 4.0 g: 2.0 g, and different reaction periods (RP) (5 minutes, 7.5 minutes and 10 minutes) were conducted to validate the optimum conditions by optimisation plot using Minitab software version 17, whereas the weight load used for drying silver nitrate-impregnated filter paper (DW) and drying period of silver nitrate-impregnated filter paper (DP) were fixed at low levels i.e. 100 g and 20 seconds, respectively, as both were found to be insignificant factors. The optimization plot (Fig. 13) shows the effect of each factor on the responses or composite desirability. The vertical red lines on the graph represent the current factor settings. The numbers displayed in bracket show the current factor level settings (in red). Both horizontal blue dash lines and numbers indicated by y which represents the responses for the current factor level. The plot displays the optimum mass ratio of sulfamic acid to zinc powder (MSZ) and the optimum reaction period (RP).

Figure 13: Optimization plot for Arsenic (III) detection   Click here to View Figure

 

Conclusion

In this work, various effects were investigated using 24 full factorial design for detection of arsenic (III) by colorimetric incorporated with image processing technique. The mass ratio of sulfamic acid to zinc powder was the most significant factor affected RGB color values and followed by reaction period. Drying weight-drying period of silver nitrate-impregnated filter-paper-reaction period (DW x DP x RP) interaction as well as drying weight-mass ratio of sulfamic acid to zinc powder-reaction period (DW x MSZ x RP) interaction significantly affected red and green color values, thus significantly influenced the detection. The optimum conditions for detection of arsenic (III) were found to be using 1 g of sulfamic acid and 0.5 g of zinc powder at 5 minutes. The present work also demonstrates that the developed method can be used to detect arsenic (III) rapidly and easily.

Acknowledgments

The authors thank to Ministry of Higher Education for financing this work via research grant (PRGS/1/2012/STWN01/UPNM/02/1) and Universiti Pertahanan Nasional Malaysia for providing the research facilities.

References

1. Kathleen, M. M.; Hoang, T. H.; Kyoung-Woong, K. Rev. Environ. Health. 2011, 26(1), 71–78.
2. Cullen W. R.; Reimer K. J. Chem. Rev. 1989, 89(4), 713–64.
3. Mizumura, A.; Watanabe, T.; Kobayashi, Y.; Hirano, S. Toxicol. Appl. Pharmacol. 2010, 242(2), 119–125.
4. Shen, S.; Li, X.-F.; Cullen, W.R.; Weinfeld, M.; Le, X.C. Chem. Rev. 2013, 113(10), 7769-7792.
5. Bednar, A.J.; Garbarino, J.R.; Burkhardt, M.R.; Ranville J.F.; Wildeman T.R. Water Res., 2004, 38, 355–364.
6. Wang, Y.; Pan., G.; Wang, K.Q. Nanotech 2011: Technical Proceedings of the 2011 NSTI Nanotechnology Conference and Expo, Boston, MA, 2011, 3, 521-524.
7. Safarzadeh-Amiri, A.; Fowlie, P.; Kazi, A.I.; Siraj, S.; Ahmed, S.; Akbor, A. Sci. Total Environ. 2011, 409, 2662–2667.
8. Anderson, R.D.; McNeill, L.S.; Edwards, M.; Morton, S.C. J. Environ. Eng. 2008, 134(5), 382-388.
9. Cherukuri, J.; Anjaneyulu, Y. Int. J. Environ. Res. Public Health. 2005, 2(2), 322 – 327.
10. Ong, K. K.; Zainuddin, M.; Teoh, C. C.; Yusof, N. A.; Wan Yunus, W. M. Z.; Mohd Azmi, A. F. Environ. Eng. Manag. J. 2015, 14(8), 1963-1968.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.