Insights into the Reaction Mechanism of the Tetrahydrobenzo [b] pyran by means of Kinetic Studies in the Presence of Fructose as a Green Catalyst

Introduction

A significant tool for synthesize in organic chemistry is multiple component reaction (MCR) method with via solvent-free or in water [1-4]. The multicomponent process (MCPs) provides a powerful method for the construction of a variety of chemicals including pharmaceuticals, complex organic molecules, and biological active compounds in a time and cost effective approach. Significant consideration has been focused on MCPs because of their valuable features such as high efficiency, mild conditions, simplistic completion, lower costs, shorter reaction times, higher atom-economy, energy saving, and environment friendliness [5-12]. An important source with various applications in biology, pharmacology and diseases therapy is 4H-Pyran nucleus. These compounds are also employed in industrial and biodegradable agrochemicals [13-22]. Organic chemists encouraged to develop efficiencies and procedures for synthesis of these kinds of compounds [23-26]. Development of catalytic systems with special properties as environment friendly, commercially available is a big challenge in the recent decays [27]. Therefore, kinetic and mechanistic studies of such compounds via catalyst has attracted our interest. Many kinetic investigations of different reactions have previously been reported using spectrophotometry techniques [28-45].

As part of our ongoing pursuit for the kinetics and mechanistic investigations of various reactions [46-58], we herein investigated the kinetic and mechanism of multicomponent reaction between 4-methoxybenzaldehyde (1), malononitrile (2), and dimedone (3) in the presence of fructose as a catalyst in a mixture of water and ethanol. Synthesis of substituted tetrahydropyridines has been previously reported by N. Hazeri and et al [59].

Figure 1: The reaction between 4-methoxybenzaldehyde 1, malononitrile 2 and dimedone 3 in the presence of fructose in a mixture of water and ethanol solvents.   Click here to View Figure

 

Chemicals and Apparatus Used

The 4-methoxybenzaldehyde (1), malononitrile (2) dimedone (3) and Fructose were obtained from Merck (Darmstadt, Germany), Acros (Geel, Belgium) and Fluka (Buchs, Switzerland), and used without further purifications. All extra pure solvent also obtained from Merck (Darmstadt, Germany). A Cary UV-vis spectrophotometer model Bio-300 with a 10 mm light-path quartz spectrophotometer cell was employed throughout the current work. Conditions for optimizing and following the reaction was chosen (2×10^-3 M) in accordance with the reported work [60].

Results and Discussions

Kinetics

The reaction of 4-methoxybenzaldehyde 1, malononitrile 2 and dimedone 3, in the presence of fructose was followed by UV-Vis spectrophotometry technique. First, selection of an appropriate wavelength for kinetic study was necessary. For this reason, in the first experiment, 10^-2 M solution of each reactant 1, 2, 3 and 2×10^-3 M solution of Fructose were prepared in a mixture of water and ethanol (2:1) as a solvent. Approximately 0.3 mL aliquot from each reactant was pipetted into a 1.2 mL light path quartz spectrophotometer cell and the relevant spectrum of each compound at 35°C was recorded over the wavelength range 200-600 nm. In the second experiment, 0.8 mL aliquot of 8×10^-3 M solution catalyst and 0.8 mL aliquot of 4×10^-2 M solution of reactants 1 and 2 were pipetted into a quartz spectrophotometer cell then 0.8 mL aliquot of 4×10^-2 M solution of reactant 3 was added to the mixture according to the stoichiometry of each reactant in the overall reaction. The reaction was monitored by recording scans of the entire spectra with 2 minute intervals during the whole reaction time at the ambient temperature (Fig. 2). As can be seen in Fig. 2, B the appropriate wavelength was discovered to be 390, 395, 400, and 405 nm (corresponding mainly to the product). Since at these wavelengths, reactants 1, 2, 3 and Fructose have relatively no absorbance value (in comparison with the relevant spectrum of each compound), it gave us the chance to find the practical conditions for following the kinetics and mechanism of the reaction. Herein, in all the experiments, the UV-vis spectrum of the product was measured over the concentration range (10^-3M ≤ M product ≤10^-2M) to confirm a linear relationship between the absorbance and concentrations values.

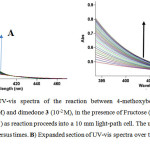Figure 2A):  The UV-vis spectra of the reaction between 4-methoxybenzaldehyde 1 (10-2 M), malononitrile 2 (10-2 M) and dimedone 3 (10-2 M), in the presence of Fructose (2×10-3 M) in a mixture of water and ethanol (2:1) as reaction proceeds into a 10 mm light-path cell. The upward arrow indicate the progress of product versus times. B) Expanded section of UV-vis spectra over the wavelength range 390-420 nm.   Click here to View Figure

 

In the third experiment under same concentration of each reactant (10^-2 M), experimental absorbance curve was recorded versus time at 35°C temperature and wavelength of 395 nm. This graph can be seen in Fig. 3, the experimental absorbance curve (dotted line) exactly fits to the second order curve (solid line). It is obvious that the reaction is second order. In this case, overall order of rate low can be written as: a+b+g= 2.

Rate=k_ovr[1]^α[2]^γ[3]^β[Cat]                                                                                                   (1)

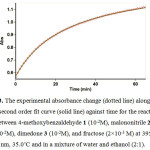Figure 3: The experimental absorbance change (dotted line) along with the second order fit curve (solid line) against time for the reaction between 4-methoxybenzaldehyde 1 (10-2M), malononitrile 2 (10-2M), dimedone 3 (10-2M), and fructose (2×10-3 M) at 395 nm, 35.0˚C and in a mixture of water and ethanol (2:1).   Click here to View Figure

 

Concentration Effect

For finding the partial order of reactants 1 and 2 under pseudo-order conditions, fourth and fifth experiments was designed, respectively.  In the fourth experiment, 5×10^-3 M of reactant 1, 10^-2 M of reactant 2, 10^-2 M of reactant 3 and 2×10^-3 M of fructose were used. The rate law for fourth experiment can be expressed:

rate = k _ove[1]^α[2]^β[3]^γ[Cat]

rate = k_obs[1]^α[Cat]                            (2)

k_obs = k_ove [2]^β[3]^γ

And also in fifth experiment, 10^-2 M of reactant 1, 5×10^-3 M of reactant 2, 10^-2 M of reactant 3 and 2×10^-3 M of fructose were applied.  The rate law can be written

rate = k _ovr[1]^α[2]^β[3]^γ[Cat]

rate = k_obs[2]^β [Cat]                            (3)

k_obs = k_ovr[1]^α[3]^γ

In the fourth experiment the original experimental absorbance curves versus times provided a pseudo-first order (Fig. 4. A). The experimental absorbance curve versus times along with a first-order fit for this experiment was recorded at 395 nm and 35.0˚C. Then, the rate constant, of the reactions were automatically obtained by the software program [60]. Herein, according to equation 2, partial order with respect to compound 1 is 1 (a=1). For recognizing of the partial order with respect to compound 2, in the fifth experiment, the experimental absorbance curve versus times provided a first-order fit (Fig. 4. B) at 395 nm and 35.0˚C. Hence, in accord with experiments, we can write equation 3 which indicats the partial order with respect to compound 2 is one (β=1).

With respect to the results of third, fourth and fifth experiments:

a+β+ γ =2 from the third experiment, a=1 on the basis of fourth experiment and β=1 based on fifth experiment. Therefore the partial order of compound 3 can be determined as zero (γ =0) and the experimental rate law can be expressed:

rate= k_obs [1][2]                                      (4)

k_obs = k_ovr [Cat]

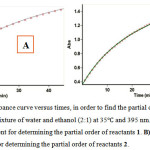Figure 4: The experimental absorbance curve versus times, in order to find the partial order of reactants 1 and 2 under pseudo-order conditions in a mixture of water and ethanol (2:1) at 35 and 395 nm. A) Obtained pseudo-first order fit curve in the fourth experiment for determining the partial order of reactants 1. B) Obtained pseudo-first order fit curve in the fifth experiment for determining the partial order of reactants 2.   Click here to View Figure

 

Effect of temperature and solvent

For determining the effect of temperature and solvent environment on the reaction rate, previous experiments were repeated under various temperatures and solvents. For this purpose, a mixture of ethanol and water (water/ethanol, 2:1, 58.6 D) and another mixture of ethanol and water (water/ethanol, 1:1, 52.7 D) have been used in the experiment. In the presence of solvent with high dielectric constant (water/ethanol, 2:1) rate of the reaction speed up at all temperatures investigation. The obtained rate constants are listed in Table 1 under different temperatures and solvents.

Table 1:  k_obs (M^-2min^-1) for the reaction between 1 (10^-2 M), 2 (10^-2M) and 3 (10^-2 M) and fructose (2×10^-3 M) in different solvent media and temperatures. 

Solvent: mix of water/ethanol (1:1) (52.7)a
T	T=308.15 K	T=313.15 K	T=318.15 K	T=323.15 K
kobs	1.95 (0.0014)b	3.15 (0.0012)	5.60 (0.0025)	7.80 (0.0016)
Solvent: mix of water/ethanol (2:1) (58.6)a
T	T=308.15 K	T=313.15 K	T=318.15 K	T=323.15 K
kobs	2.40	3.75	6.21	8.47
	(0.0025)b	(0.0018)	(0.0012)	(0.0019)
kovr = k obs /[cat]	1.20 × 10+3	1.88 × 10+3	3.11 × 10+3	4.24 × 10+3
ln ( kovr  / T )	1.36	1.79	2.28	2.57
T × ln ( kovr / T)	418.93	560.44	724.83	831.47

^a: dielectric constant (D)

^b: standard deviation (SD).

As can be seen in Table 1, rate of reaction was accelerated with increase of temperature. Increasing rate constants with high dielectric solvent indicate that at the rate determining step, active complex must have more charges rather than reactant species ,therefore, solvent stabilize active complex more than reactant species. The second-order rate constant (ln k_ovr) of the reaction was inversely proportional to the temperature, which is agreement with the Arrhenius equation. This behavior is shown in Fig. 7. The activation energy, for the reaction between 1, 2, 3 and fructose was calculated in the mixture of water and ethanol (2:1) (E_a = 71.05 ± 1.39 kJ ⁄ mol) form the slope of Fig. 7.

Figure 5: The spectulative mechanism of the tetrahydrobenzo[b]pyran formation   Click here to View Figure

 

The activation parameters which involve DG^ǂ, DS^ǂ and DH^ǂ can be now calculated by the Eyring equation (Fig. 6A, equation 5). Fig. 6B shows also a different linearized form of Eyring equation (equation 7). The standard errors for activation parameters have been calculated and reported for both used forms of Eyring equation in Fig. 6(A,B) [61].

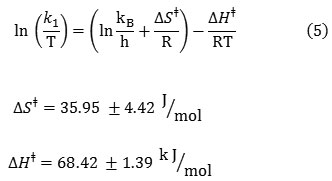
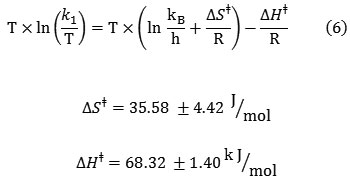
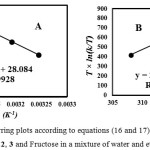Figure 6(A,B): Eyring plots according to equations (16 and 17), for the reaction between 1, 2, 3 and Fructose in a mixture of water and ethanol (2:1).   Click here to View Figure

 

The value of calculated activation parameters (DS^ǂ, DH^ǂ and DG^ǂ)have been listed for the reactions between 1, 2, 3 and fructose in a mixture of water and ethanol (2:1), at 308.15 K in Table 2.  

Table 2: Activation parameters for the reaction between compounds 1, 2, 3 and fructose measured in different solvent media.

water/ethanol	DHǂ(kJ mol-1)	DSǂ (Jmol-1)	DGǂ(kJ mol-1)	Ea (kJ ⁄ mol)
(2:1) (58.6)a	68.32 ± 1.40	35.58 ± 4.42	57.35 ± 2.76	70.88 ± 1.40b	71.05 ± 1.39c
(1:1) (52.7)a	75.71 ± 1.71	57.83 ± 5.43	57.88 ± 3.37	78.27 ± 1.71b	78.45 ± 1.70c

a: dielectric constant (D)

b: according to this equation: Ea = DHǂ + RT

c: in accord with the Arrhenius equation

Overall, it can be seen that activation enthalpy (DH^ǂ) and free energy of activation (DG^ǂ) are positive and have rather large values which suggest that the energy required for the reaction is relatively high, The high enthalpy of activation results because bonds need to be broken before the transition state.

Looking at detail, the activation enthalpy was lower in the presence of solvent with high dielectric constant (water/ethanol, 2:1), at the same temperature, and this give rise to lower activation energy for reaction in solvent with high dielectric constant because E_a is directly proportional to the activation enthalpy Ea = DH^ǂ + RT .

Speculative Mechanism

With regarding of the obtained results, a simplified scheme of the speculative mechanism is shown in Fig. 5.

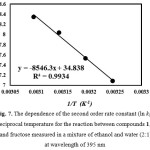Figure 7: The dependence of the second order rate constant (ln k1) on reciprocal temperature for the reaction between compounds 1, 2, 3 and fructose measured in a mixture of ethanol and water (2:1) at wavelength of 395 nm Click here to View Figure

 

For investigating the rate-determining step of the speculative mechanism, the rate law can be written for the final step of reaction:

Rate = k₄[I₃][Cat]                                                                                                    (7)                                                                                                                                     For obtaining the concentration of [I₃], the steady state approximation was applied as below:

k₃[I₂] = k₄[I₃]                                                                                                                        (9)

The value of equation 9 was replaced in the equation 7, therefore the rate equation can be obtained:

Rate = k₃[I₂][Cat]                                                                                                (10)

The concentration of intermediate [I₂] can be obtained as follow:

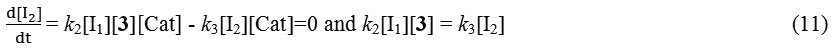
And with the replacement of the equation 11 in 10 the following equation is obtained:

Rate = k₂[I₁][3][Cat]                                                                          (12)

And we can obtain the value of [I₁] as below for generation of equation 15:

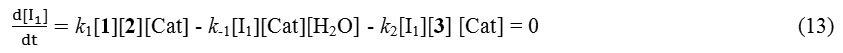
k₁[1][2] = [I₁](k_-1[H₂O] + k₂[3])                                                                                          (14)

The equation 15 is the general rate law for the reaction. As can be seen, steps 3 and 4 have no chance to be the RDS since equation 15 is independent of k₃ and k₄ rate constants. Also, the concentration of the compound 3 appears in the equation 15, and this is not compatible with the experimental data because the experimental rate law shows that the rate law is free of the concentration of compound 3 (With respect to the results: a+β+ γ =2 from the third experiment, a=1 on the basis of fourth experiment and β=1 based on the fifth experiment). On contrary, this is possible for steps 1 and 2 (see equation 15). If step 2 is a RDS, as a result, the following speculation is logical: k₂[3] << k_-1[H₂O][Cat]

In this case, the rate law becomes:

Equation 16 is not consistent with the experimental rate law (equation 4) because the overall order of reaction is three, in addition, it depends on the concentration of compound 3.

If step 1 is a RDS, in this case:

k₂[3] >> k_-1[H₂O][Cat]

The rate law can be expressed:

Rate = k₁[1][2][Cat]                                                                                    (17)

Rate = k_obs[1][2]                                                                                                               (19)

The final equation 19 which obtained from the steady state assumption and the mechanism of the reaction is in agreement with the experimental equation 4 and indicates that the overall order of the reaction is two. In addition, the partial order with respect to each reactant 1, 2 and 3 is one, one and zero, respectively. Due to the presence of k₁ in the rate low (equation 17), it obvious that the first step (k₁) is overall rate constant (k_{1 =} k_ovr, deduced from comparison between equation 4 and 17). Therefor step 1 (k₁) is a rate determining step (RDS), and step 2 (k₂) is a fast step. Herein, the transition state (step 1, Fig. 5) carries a dispersed charge in reaction, so solvents with higher dielectric constant speed up the reaction rate by stabilizing the species at the transition state more than reactants, and therefore E_a would be lower (Table 3, 2 and 1).

Conclusion

The overall order of reaction for the synthesis of tetrahydrobenzo[b]pyran in the presence of fructose showed second-order kinetics and the partial orders with respect to 4-methoxybenzaldehyde 1, malononitrile 2 and dimedone 3 were one, one and zero, respectively. Rate of reaction accelerates in solvent with high dielectric constant. The second-order rate constant of the reaction was proportional to the temperature and was in agreement with the Arrhenius equation. The first step of the speculative mechanism was recognized as a rate-determining step (k₁) confirmed by the steady-state approximation. From the temperature, concentration and solvent studies, the activation energy (E_a = 71.05 ± 1.39 kJmol^-1) and the related activation parameters (ΔG^‡ = 57.35 ± 2.76 kJmol^-1, ΔS^‡ = 35.58 ± 4.42 Jmol^-1 and ΔH^‡ = 68.32 ± 1.40 kJ mol^-1) were calculated.

Acknowledgement

We gratefully acknowledge the financial support received from the Research Council of the University of Sistan and Baluchestan.

References

1. Hassan, V.; Ashraf, F.; Mol Divers, 2011, 15, 233.
2. Gelens, E.; De Kanter, FJJ.; Schmitz, RF.; Sliedregt, LAJM.; Van Steen, B.J.; Kruse, CG.; Leurs, R.; Groen M.B.; Orru R.V.A.; Mol. Divers. 2006, 10, 17.
3. Shaabani, A.; Maleki, A.; Rezayan, A.H.; Sarvary, A.; Mol. Divers. 2011,15, 41.
4. Xin, X.; Wang, Y.; Kumar, S.; Liu, X.; Lin, Y.; Dong, D.; Org. Bimol. Chem. 2010, 8, 3078.
5. Elders, N.; Van der Born, D.; Hendrickx, L.J.D.; Timmer, B.J.J.; Krause, A.; Janssen, E.; De Kanter, F.J.J.; Ruijter, E.; Orru, R.V.A.; Angew. Chem. Int Ed. 2009, 48,5856.
6. Bonfield, E.R.; Li, C.; J. Adv. Synth. Catal. 2008, 350.
7. Dömling, A.; Chem. Rev. 2006,17, 106.
8. Ramón, D.J.; Yus, M.; Angew. Chem. Int Ed. 2005, 44, 1602.
9. Dömling, A.; Ugi, I.; Angew. Chem. Int Ed. 2000,39, 3168.
10. Chapman, CJ.; Frost, C.G.; Synthesis. 2007, 01, 1.
11. Sun, W. B.; Zhang, P.; Fan, J.; Chen, S. H.; Zhang, Z.H.; Synth. Commun. 2010, 40, 587.
12. Symeonidis, T. M.; Chamilos, D.J.; Hadjipavlou-Litina, M.; Kallitsakis, K.E.; Litinas. Bioorg. Med. Chem. Lett. 2009, 19, 1139.
13. Mohr, S. J.; Chirigos, M. A.; Fuhrman, F. S.; Pryor, J. W.; Cancer. Res. 1975, 35, 3750.
14. Wang, J. L.; Liu, D.; Zhang, Z.; Shan, S.; Han, X.; Srinvasula, S. M.; Croce, C. M.; Alnemeri, E. S.; Huang, Z.; Proc Natl Acad Sci USA. 2000, 97, 7124.
15. Darbarwar, M.; Sundarmurthy, V.; Synthesis. 1982, 337.
16. Ghosal, S.; Murugandam, V.; Mukhopadhyay, B.; Bhattacharya, S.; Ind J Chem. 1997, 36B, 596.
17. Khafagy, M. M.; El-Wahas, A. H. F. A.; Eid, F. A.; El-Agrody, A. M.; Farmaco. 2002, 57, 715.
18. Bianchi, G.; Tava, A.; Agric. Biol. Chem. 1987, 51, 2001.
19. Hiramoto, K.; Nasuhara, A.; Michiloshi, K.; Kato, T.; Kikugawa, K.; Mutat Res. 1997, 47,395.
20. Anderson, D. R.; Hegde, S.; Reinhard, E.; Gomez, L.; Vernier, W. F.; Lee, L.; Liu, S.; Sambandam, A.; Snider, P. A.; Masih, L.; Bioorg MedChem Lett. 2005, 15, 1587.
21. Skommer, J.; Wlodkowic, D.; Matto, M.; Eray, M.; Pelkonen.; J. Leukemia. Res. 2006, 30, 322.
22. Eiden, F.; Denk, F.; Arch Pharm Weinhein Ger (Arch Pharm). 1991,324, 353.
23. Poyser, R.H.; Hamilton, T.C.; Drugs of the Future. 1994, 19, 39.
24. Empfield, J.R.; Russell, K.; Annu Rep Med Chem. 1996, 30, 81.
25. Pirotte, B.; Fontaine, J.; Lebrun, P.; Curr Med Chem. 1995, 2, 573.
26. Atwal, K.S.; Curr Med Chem. 1996, 3, 27.
27. Debecker, D.P.; Gaigneaux, E.M.; Busca, G.; Chem. Eur J. 2009, 5, 3920.
28. Langer, S.; Ljungström, E.; Ellermann, T.; Nielsen, O.J.; Sehested, J.; Chem. Phys. Lett. 1995, 53, 240.
29. Ivanov, V.V.; Decker, C.; Polym. Int. 2001, 50,113.
30. Fung, P.C.; Sin, K.M.; Tsui, S.M.; Coloration. Technology. 2000, 116,170.
31. Misiti, F.; Castagnola, M.; Zuppi, C.; Giardina, B.; Messana, I.; Biochem. J. 2001, 356, 799.
32. Brudnik, K.; Twarda, M.; Sarzyński, D.; Jodkowski, J.T.; J. Mol. Model. 2013, 19,1489.
33. Almandoz, M.C.; Dávila, Y.A.; Sancho, M.I.; Gasull, E.I.; Blanco, S.E.; Spectrochimica. Acta. Part A: Molecular and Biomolecular Spectroscopy. 2010, 77, 51.
34. Lu, L.L.; Li, Y.H.; Lu, X.Y.; Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy. 2009, 74, 829.
35.  Tatarchuk, V.V.; Sergievskaya, A.P.; Druzhinina, I.A.; Zaikovsky, V.I.; J. Nanopart. Res, 2011, 13, 4997.
36.  Bugarcic, Z.D.; Rosic, J.; Petrovic, B.; Summa, N.; Puchta, R.; Eldik, R.V.; J. Bio. Inorg. Chem. 2007, 12, 1141.
37.  Rvovic, M.D.; Divac, V.M.; Puchta, R.; Bugarčić, Z.M.; J. Mol. Model. 2011, 17, 1251.
38.  Bugarcic, Z.D.; Rosic, J.; Petrovic, B.; Summa, N.; Puchta, R.; Eldik, R.V.; J. Bio. Inorg. Chem. 2007, 12, 1141.
39. Erasmus, J.J.C.; Conradie, M.M.; Conradie, J.; Reac. Kinet. Mech. Cat. 2012, 105, 233.
40.  Rilak, A.; Petrovic, B.; Grguric´-Šipka, S.; Tešic, Z.; Bugarcˇic, Z.D.; Polyhedron. 2011,30, 2339
41.  Kalyan, BP.; Gupta, K.S.; Transition. Met. Chem. 2012, 37, 671.
42.  Chandra, AK.; J. Mol. Model. 2012, 18, 4239.
43.  Sandhiya, L.; Kolandaivel, P.; Senthilkumar, K.; Struct. Chem. 2012, 23, 1475.
44.  Pandeeswaran, M.; Elango, K.P.; J. Sol. Chem. 2009, 38, 1558.
45.  Altun, O.; Akbas, H.; J. Chem. Thermodynamics. 2007, 39, 1413.
46.  Shaharaki, M.; Habibi-Khorassani, S.M.; Ebrahimi, A.; Maghsoodlou, M.T.; Paknahad, A.; Prog. React. Kinet Mech. 2012, 37, 321.
47.  Shahraki, M.; Habibi‐Khorassani, S. M. J Phys Org Chem. 2015, 28 (6), 396-402.
48.  Pourpanah, S. S.; Habibi-Khorassani, S. M.; Shahraki, M. Chinese J Catal. 2015, 36(5), 757-763.
49.  Habibi-Khorassani, S.M.; Maghsoodlou, M.T.; Ebrahimi, A.; Zakarianejad, M.; Fattahi, M.; J. Sol. Chem. 2007, 36, 1117.
50. Habibi-Khorassani, S.H.; Maghsoodlou M., Ebrahimi A., Zakarianejad, M.; Mohammadzadeh, P.; Shahraki, M. Orient J Chem. 2008, 24, 73.
51. Habibi-Khorassani S. M.; Shahraki, M.; Dehdab, M.; Poorshamsoddin, M. A. J Solution Chem. 2015, 44, 2154.
52. Habibi-Khorassani, S.M.; Maghsoodlou, M.T.; Ebrahimi, A.; Zakarianejad, M.; Mohammadzadeh, P.; Shahraki, M.; Int. J. Chem. Sci. 2008, 6, 647.
53. Shahraki, M.; Habibi-Khorassani, S. M.; Dehdab, M. RSC Adv. 2015, 5(65), 52508-52515.
54. Dehdab, M.; Habibi-Khorassani, S.; Shahraki, M., Catal Lett. 2014, 144(11), 1790-1796.
55. Yogananth, A.; Sheik Mansoor, S. Orient J Chem. 2015, 31(1), 17-23.
56. S. M. Habibi-Khorassani, M. T. Maghsoodlou, M. Shahraki, S. Talaie Far, M. R. Mousavi. Adv in Phys Chem. 2014, 1.
57. Yaghoubian, H.; Habibi-Khorassani, S.M.; Ebrahimi, A. Orient J Chem, 2015, 31(4), 2107-2113.
58.  Zakarianejad, M.; Ghasempour, H.; Habibi-Khorassani, S.M.; Maghsoodlou, M.T.; Makiabadi, B.; Nassiri, M.; Ghahghayi, Z.; Abedi, A.; ARKIVOC. 2013, (iv), 171.
59. Nourallah, H.; Maghsoodlou, M. T.; Mir, F.; Kangani, M.; Saravani, H.; Molashahi, E.; Chinese. Journal of Catalysis. 2014, 35, 391.
60. Schwartz.; Gelb, L. M.; R. I., Anal. Chem. 1978, 50, 1592.
61. Lente, G.; Fabian, I.; Poe, A.J.; New. J. Chem. 2005, 29, 759.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.