A Study of Fe₃O₄@ Si₁₈O₂₇ Catalyst Through Statistical-Nucleus Independent Chemical Shifts(S-NICS) Method

Introduction

Electronic towards the structural aspects have proved to be an important key in physical organic chemistry in the explanation of structures, reactivity and stabilities of various organic compounds and natural product molecules¹ .

The chemical shift of a nucleus in molecular rings occurs from the nuclear shielding effect of an applied magnetic field. The magnitude of such an induced magnetic field is commensurate with the stability of the applied external magnetic field (B₀).  Thus the effective field (B_eff) at the nucleus is given by B_eff = B₀ (1− σ_i), where “1” is the unit matrix and σ_i is the second-rank nuclear shielding matrix. In ordinary NMR experiments B₀ is a uniform field along the z-axis and the resonance NMR frequency, ν_i, of a given nucleus in a molecule is therefore dependent to its gyromagnetic ratio, γ_i, as specified by ν_i = (γ_i/2π)B₀(1 − σ_i)^2.

The nucleus-independent chemical shift (NICS) is a computational method that calculates the absolute magnetic shielding at the center of the ring taken with reversed sign. Negative NICS values indicate aromaticity and positive values antiaromaticity^3-5 .

For further investigation of aromaticity, another method called the harmonic oscillator model of aromaticity (HOMA)⁶ has been applied, and is distinguished as a normalized sum of the squared deviations of bond length from the normal value⁷.An aromatic compound has a HOMA value of one whereas a non-aromatic compound has the value 0.

Several criteria for explanation of aromaticity can be considered and may divided into five categories, which are: (1) the energetic approach to aromaticity (2) geometrical considerations (3) reactivity of aromatic compounds (4) magnetic parameters of aromaticity^8-10, and the (5) Statistical-Nucleus-Independent Chemical Shifts approach (S-NICS) which is the subject of this work.

In using the energetic criterion for establishing the aromaticity of a compound, it is evident that the excess of stability of the structure is due to cyclic electron delocalization relative to suitable references systems^11-12 . Moreover, Cooper, Gerratt, and Raimondi¹³ have developed some appropriate reference systems for calculation of the resonance energy. In using structural considerations, the geometry should show a decrease in aromaticity of bond alternation which have been reported by Julg and Kruszewski in several quantitative measurements¹⁴ . Monajjemi and Boggs have shown the low aromaticity of borazine in the rings of B₁₈N₁₈ and B₁₅N₁₅ by the non-bonded interaction method^15-18 .

Regarding NMR chemical shifts and diamagnetic susceptibilities, protons attached to aromatic rings typically undergo a downfield shift from the olefin region; therefore, an up-field shift appears in the proton NMR spectrum¹⁹ . So aromaticity can be defined as the ability of a compound to sustain an induced ring current, these compounds are then called dia-tropic and antiaromatic compounds are called Para-tropic. NMR chemical shifts and diamagnetic susceptibilities , anisotropy is important when measuring a compound’s aromaticity ²⁰.

Recently aromaticity in terms of nucleus-independent chemical shifts in long distances of NICS (1, 2.5, 3, and 3.5) Å, around the ring center, NICS (0), at the center of ring plane and aromatic ring current shielding (ARCS) were compared in several studies. In short range of distances (r<0.3) there are no theoretical or mathematical reports of statistical approach in nucleus independent chemical shift calculations, while the asymmetry (η) and skew (κ) parameters fluctuate in behavior around the center of rings.

For further discussion of statistical approach in nucleus independent chemical shift calculations, especially in short range of distances, we have focused in relaxations of CAS, dipole-dipole and contribution ²¹. We have shown that the asymmetry (η) and skew (κ) parameters fluctuate in behavior around the center of rings due to minimum isotropy in the center. The most fluctuations are appearing around the minimum or maximum functions mathematically.

Nuclear spin relaxation studies in the gas phase had started in 1987 ²². Spin-relaxation data in the gas phase provide a stringent test of the anisotropy of an existing intermolecular potential. In some cases, spin-relaxation data is a powerful test of the anisotropic part of the intermolecular interaction. There are other observables such as the Beenakker effects, depolarized Rayleigh scattering, sound absorption, and pressure broadening of rotational lines in the IR, which are also sensitive to the anisotropy of the potential ²³.

The basis of this work is on random motions of probes in the shielding and deshielding spaces of aromatic and antiaromatic molecules to consider maximum abundant of points in due to dipole–dipole, CSA and contribution relaxations. The main purpose of random displacement of various probes inside of shielding and deshielding spaces are for understanding of mechanism and consequences of anisotropic spin–spin interactions in short ranges, Although the relaxation of proton and hydrogen probes are much less, than the large ion probes such as Li+.

In CSA, relaxation Chemical shift anisotropy (CSA) originates from the orientation dependence of the chemical shift, and hence changes under rotation of the molecule and induces minor variations in the magnetic field at the site of the nucleus.

The time dependence of anisotropic interactions does however contribute to relaxation but the average amount can be time independent.

In this study, the major components of Haeberlen parameters, and chemical shift anisotropy (CSA) tensors have been calculated for borazine, benzene, naphthalene, B_nN_nH_x rings (n=12, 15, 18) and B₃N₃H_n (n = 0, 2, 4, 6, 8,). The numerous random points around the center of those molecules have been produced by generation of pseudo-random numbers, which are distributed in a Gaussian function in the interval [0, 1).

The hydrogenated and dehydrogenated structures of borazine and B_nN_n rings have been investigated to understand more about the unknown parameters of those rings in point of electromagnetic, aromaticity, delocalization mechanism, conjugated system and hyperactive conjugation in BN alternate systems. Therefore, the hydrogenation and dehydrogenation of borazine has moved gradually in two directions toward cyclotriborazane (B₃N₃H₁₂) and B₃N₃ respectively .

Our result has been compared by the energy decomposition analysis (EDA) method . The total  bonding energy and the  conjugation between three B-N  bonds in borazine is significantly smaller than that for benzene and magnetically properties shows a singular behavior in borazine and B₃N₃H_x rings .

Fowler and Steiner computed the total current density induced by a magnetic field perpendicular to the molecular plane of borazine. They found that the  currents are localized in three islands of circulation on the nitrogen atoms and concluded that borazine is moderately aromatic . Nucleus-independent chemical shift values (NICS) show a little and no evidence of ring currents, indicating with no aromaticity for borazine due to the polar B–N bond .In contrast, the S-NICS data shows a weak but stable aromaticity for borazine according to the 1999 definition provided by IUPAC definition of aromaticity.

We have optimized various isomers of B₃N₃ and B₄N₄ to understand which members of each group are more stable.  Scheme 1 shows that in both groups the planar ring isomer of B₃N₃ and B₄N₄ with B and N alternate are more stable than the others.

We have discussed the electronic properties in their structures to find the reason for relative stability in these rings in point of isotropy and anisotropy. Finally the electronic structures of B_nN_n rings of (B₃N₃) _N for (N= 4, 5, 6) of B₁₂N_12, B₁₅N₁₅ and B₁₈N₁₈ has been studied by S-NICS method ²⁴.

Magnetite (Fe3O4) is the earliest discovered magnet which crystallizes in the inverse cubic spinel structure. Each cubic spinel cell contains eight interpenetrating oxygen and the tetrahedral sites, occupied by one-third of the iron atoms, form a diamond structure. The remaining Fe atoms are located at the octahedral sites with the nearest-neighbor atoms lined up as strings along six different [110] directions. In other words Fe₃O₄ consists of a cubic close packed array of oxide ions where all of the Fe²⁺ ions occupy half of the octahedral sites and the Fe³⁺ are split evenly across the remaining octahedral sites and the tetrahedral sites .

Both FeO and γ-Fe₂O₃ have a similar cubic close packed array of oxide ions and this accounts for the ready interchangeability between the three compounds on oxidation and reduction as these reactions entail a relatively small change to the overall structure therefore, Fe₃O₄ samples can be non-stoichiometric²⁵ .

Fe₃O₄ is ferromagnetic with a curie temperature of 858 K and The ferromagnetism of Fe₃O₄ arises because the electron spins of the Fe^II and Fe^III ions in the octahedral sites are coupled and the spins of the Fe^III ions in the tetrahedral sites are coupled but anti-parallel to the former. Fe₃O₄ is used as a catalyst in the Haber process and in the water gas shift reaction .

The latter uses an HTS (high temperature shift catalyst) of iron oxide stabilized by chromium oxide . This iron-chrome catalyst is reduced at reactor start up to generate Fe₃O₄ from α-Fe₂O₃ and Cr₂O₃ to CrO₃ . Fe₃O₄ is an electrical conductor with conductivity significantly higher than Fe₂O₃, and this is ascribed to electron exchange between the Fe^II and Fe^III centers ²⁵

Magnetite particles are of interests in bioscience applications such as in magnetic resonance imaging (MRI) since iron oxide magnetite nanoparticles represent a non-toxic alternative to currently employed gadolinium-based contrast agents. However, due to lack of control over the specific transformations involved in the formation of the particles, truly super paramagnetic particles have not yet been prepared from magnetite, i.e. magnetite nanoparticles that completely lose their permanent magnetic characteristic in the absence of an external magnetic field .
As a half-metallic material, Fe3O4 shows normal metallic behavior in the minority spin, while
at the same time there is a gap of~0.5 eV in the majority spin at the Fermi level. From an itinerant point of view, the high conductivity (~250 -1 cm-1) of the high-temperature phase is a natural consequence of the partially filled 3 d band of the octahedral -site Fe atoms .

Production of nano-particles can be performed chemically by taking for example mixtures of Fe^II and Fe^III salts and mixing them with alkali to precipitate colloidal Fe₃O₄. The reaction conditions are critical to the process and determine the particle size .Nano particles of Fe₃O₄ are used as contrast agents in MRI scanning.Magnetic nanoparticles have attracted much interest not only in the field of magnetic recording but also in the areas of medical field of magnetic sensing. Especially, nanoparticles of iron oxide are reported to be applicable as a material for use in drug delivery systems, cancer therapy and MRI .

On the other hand, most of the applications require magnetic particles to disperse in a non-magnetic matrix. The matrixes play an important role in determining physical properties of the composite nanoparticle in addition to providing a means of particle dispersion.

Another important characteristic of the matrix is to act as the protection of magnetic nanoparticles against corrosion or oxidation especially in the case of metallic nanoparticles . Among carbon-based or oxide matrixes such as silica, alumina, titanic oxide or zeolite, silica can be a most suitable material for the matrix because of its non-toxicity, inertness to magnetic field and easiness to form cross-lined network structure .

Silica surfaces are chemically stable, biocompatible and can be easily functionalized for bio conjugation purpose. Hence silica-coated magnetite composite nanoparticles (Fe3O4@SiO2) have been synthesized by many groups . Recently, silica coated magnetite functionalized with γ-mercapto-propyl-trimethoxy-silane have been successfully applied to extract Cd2+, Cu2+, Hg2+, and Pb2+ from water in a wide pH range .

Catalysts play a very important role in modern science and technology as they improve reaction yields; reduce temperatures of chemical processes in synthesis.There are two main types of catalysis, heterogeneous, where the catalyst is in the solid phase with the reaction occurring on the surface and homogeneous, where the catalyst is in the same phase as the reactants .

The heterogeneous catalysts can be readily separated from the reaction mixture but the reaction rate is restricted due to their limited surface area . Meanwhile homogeneous catalysts can react very fast and provide a good conversion rate per molecule of the catalyst, but since they are miscible in the reaction medium, it can be a painstaking process to remove them from the reaction medium . The difficulty in removing homogenous catalysts from the reaction medium leads to problems in retaining the catalyst for reuse . The bridge between heterogeneous and homogeneous catalysts can be achieved through the use of Fe3O4 nanoparticles . Fe3O4 particularly is useful and important group of nanoparticles in the magnetic nanoparticles (MNPs) groups which show strong magnetic moments that are rarely retained outside of the presence of an external magnetic field. These nanoparticles may be composed of a series of materials such as metals like cobalt and nickel, alloys like iron/platinum and metal oxides like iron oxides²⁶ .and ferrites²⁷.Fe3O4 Nanoparticles of silica catalytic material provide the benefit of increased surface area which allows for an increased reaction rate²⁸. Moreover, nanoparticles can permit additional catalytic functionalities due to their unique properties²⁹.As instance, the MNPs being used to extract selected cells from biological samples and cultures³⁰.

A few catalysis of magnetic nanostructures have been developed up to now, including the preparation of nanocomposite materials consisting of magnetic core nanoparticles which have been coated by the shell of other catalytically active nanomaterials. Another type of catalyst which is of interest for organic synthesis involves the use of organic molecules. These molecules show a large degree of specificity for their reactions and may allow a more successful reaction than conventional chemistry. Overall, the binding of catalysts to magnetic nanoparticles allows the retention of these materials after the end of the reaction for reuse.

Theoretical Background

NMR Shielding

The reduced anisotropy

and anisotropy (Δσ) with relation of

including shielding asymmetry (η) can be defined as:

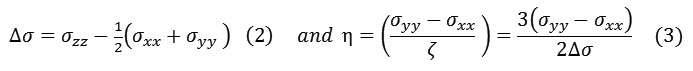
In some cases of an axially symmetric tensor,

will be zero and hence η = 0. However, the asymmetry (η) parameter indicates that how much the line figure deviates from an axially symmetric tensor, therefore, (0 ≤ η ≤ +1).

The shielding tensor can be expressed as the sum of a symmetric, an anti-symmetric, and a scalar terms, which are rank 2, rank 1 and rank zero tensors respectively as:

The total chemical shielding tensor “r” is a non-symmetric tensor that can be decomposed into three independent tensors as: (1), an isotropic component, (2) a traceless symmetric component, and (3) a traceless anti-symmetric component . In spherical tensor representation, as Haeberlen  have pointed out, at a fundamental level tensors are better represented in spherical fashion, such that a general second-order property “σ” may be written as

where the number in brackets refers to tensor rank. Spherical tensors are intrinsically involved in considering  the effects of  tensor quantities on density matrix  evolution  , so  the use of  this representation  is  inevitable  for such  work. It is worth noting that:

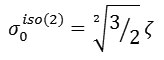
and

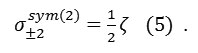
The proportionalities  in  these equations  indicate that  shielding  anisotropy  and  asymmetry  can readily  be  related  to  spherical  tensor  components,  thus  facilitating  theoretical interpretation,  whereas  the  relation  between  spherical  tensor  components  and  span/skew  is more  obscure.  The isotropic tensor can be represented by a scalar average as :

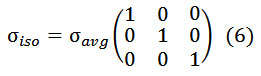
The symmetric component of the shielding tensor has tensor elements with r_ij = r_ji. This tensor is responsible for the CSA relaxation most often described in the literature and can be  diagonalized by rotation into the shielding tensor principal coordinate system.The anti-symmetric tensor also induces CSA relaxation but this is almost impossible to measure because the induced effects are close to parallel to the external magnetic field which cannot be diagonalized.

By this work, in a statistical calculation we have shown that a time independent average of (Ω^*) can be replaced of all above sum of asymmetric, an anti-symmetric, and a scalar terms, which are rank 2, rank 1 and rank zero tensors respectively. This method is based on random motions of probes in the shielding and deshielding spaces of aromatic and antiaromatic molecules to consider maximum abundant of relaxations points in due to dipole–dipole and spin –dipole interactions.

The magnetic environment of a spin is seldom isotropic. Therefore, is represented by a tensor of Span.

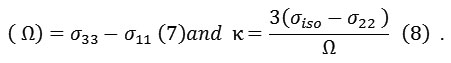
In the Herzfeld-Berger notation , tensors have explained by three parameters, which they are combination of the major components in the standard notation. Those are including, the span (Ω), which describes the maximum width of the model, (Ω ≥ 0), and the skew (κ) of the tensor which is a magnitude of the values.

The accurate formulation of the span (Ω), including the factor of (1-σ_ref) has been described by Ω = (σ₃₃– σ₁₁) (1-σ_ref) (9). In the Haeberlen-Mehring-Spiess notation, different combinations of the major components are used to explain the line figure, and is needed the major components become orderly according to their segregation from the isotropic value in this convention

The CSA relaxation rates depend on the anisotropy parameter in the standard parameters, of the shielding tensor, (σ₁₁, σ₂₂, σ₃₃), are labeled according to the IUPAC rules, and they formalized and adopt the high frequency-positive order. Therefore, σ₃₃ corresponds to the direction of minimum shielding, with the highest frequency, whenever σ₁₁ corresponds to the direction of maximum shielding, with the lowest frequency .

Moreover the orientation of asymmetry tensoris given by

; (-1 ≤ κ ≤ +1), and related on the position of σ₂₂ with consideration of σ_iso, the sign of κ is either positive or negative.

Based onour calculations especially various B_nN_n Rings, Benzene and naphthalene, (κ) is mostly positive^31-40, and the negative values are belong to some critical or boundary points. In the case of an axially symmetric tensor, σ₂₂ equals either σ₁₁ or σ₃₃ and κ= ±1 thereforea = Ω/3, and the parameter “a” and “κ” are zero when σ₂₂ = σ_isoand the parameter “μ” used with the Herzfeld-Berger is related to the span of a tensor. Meanwhile, the spinning rate is given by μ = Ω*ν_ref,

For a non-zero anti-symmetric tensor [44] give the relaxation rates

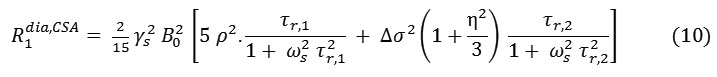
and ρ²  is defined by:

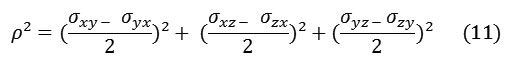
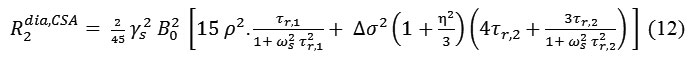
Where and   correspond to the correlation times for isotropic tumbling and small-step molecular rotation, respectively and in the case of axial symmetry (η=0) or for isotropic tumbling .

Based on recent works^41-66, in this study, we consider a model of SiO2 rings as a molecule for Fe₃O₄@SIO₂ catalyst using ab initio calculations within the density functional theory (DFT) for calculating the aromaticity of rings for organic calculations.

Results and Discussion

Total shielding constants, orientations of the principal axes such as standard components,Haeberlen-Mehring, and Herzfeld-Berger parameters for Fe3O4@Si₁₈O₂₇ in various statistical situations have been calculated by DFT methods and the data are listed in tables1-5.

In short distances of region around the molecular centers, the asymmetric parameter (η),and the skew (κ), exhibited Gaussian distribution based on their fluctuation behavior, which is dependent on their distances from the center of the molecular rings.In contrast, of those parameters, the isotropy does not have a fluctuating behavior and it increased by increasing its distance from the center of the rings with a linear relationship. The slopes of these lines are changed, and among the levels of various distances for isolated Si₁₈O₂₇ and Fe3O4@Si₁₈O₂₇(less than 0.2 Å and more than 0.2 Å for SiO2 ring, less than 0.25 Å and more than 0.25 Å for Fe3O4@Si₁₈O₂₇)(Fig.1).

The isotropy during the replacing of Fe3O4@sio2 are positive which indicates negative values for aromaticity,but the slopes are decreased from the replacing from 0.1 to center (Fig.1).

As we have shown in Fig.1-7, the slopes of aromaticity curves versus distances to the center of the Fe3O4@SiO2 ring are decreased by decreasing the distances gradually which indicates distortion of aromatic electronic structures, and on the other hand these slopes are increased by increasing the distance,emphasizing a special electronic structure in Fe3O4@SiO2. Therefore, S-NICS has an increased ability to identify exact points in the area of shielding space byaromaticity criterion in such compounds via Monte Carlo stochastic calculation.

In all previous works [3,10], different basis sets yielded isotropies of various magnitude, and the criterion ofaromaticity cannot be certain by using different methods, because in multiple calculations the numerous basis sets can evaluate different isotropies for two situations of one aromatic molecule.

It is acceptable that the difference between isotropies in NICS values can express the quality of the distinct aromaticity for a few molecules, but these differences between isotropies are not able to express the mechanism of aromaticity as well as S-NICS.

In theS-NICS method via the statistical calculations, the best point of the shielding space around the center of symmetric or non-symmetric aromatic molecules can evaluated as an aromaticity criterion. and in this method the expectation of the (η*) and (κ*)have been calculated as the Gaussian curve functions versus one , two  or three dimensional distances around the center of the SiO2 (Tables 1-4and Fig.1-7).

The isotropy (σ_iso^*) which is related to all of (η*) and (κ *)and (Ω*) and ( *) is the best criterion for various aromatic molecules by the S-NICS method, which can express both qualitative and quantitative magnitudes for symmetric or non-symmetric aromatic molecules (table 3).

So “κ” can be calculated in two ways, the first one by the expectation value of the Gaussian curve (κ*) and the second one with the eqs. (27,28). Such as stochastic rules in the Monte Carlo calculation for π = 3.14 in a circle,it is evident, that the value of the Monte Carlo calculation will be more accurate by increasing the random numbers of the stochastic test, and it is significant that |κ*- κ |→0.0 by addition of random numbers in the S-NICS method.

Similar to the NICS method, in S-NICS, negative nucleus-independent chemical shifts denote aromaticity and positive values denote antiaromaticity.In S-NICS methods, the shielding and deshielding spaces are significant to discuss the mechanism of the aromatic molecules in point of ring currents, which are the circulating π electrons in an aromatic molecule produce opposite to the applied magnetics field.

The stability of the isotropy criterion is highly affectedon the best places in the shielding area spaces and it is dependent on the structures of the aromatic rings. Soby using this method, a suitable and stable magnitude of isotropy can calculated as an aromaticity criterion. It is obvious that structural factors cause changes in the magnetic field experienced by the nuclei and change the resonant frequency.Therefore the chemical shielding and many other factors such as electronegativity,hydrogen bonding, and magnetic anisotropy of π-systems will be changed because of the electrons around the proton which produce a magnetic field, countering the applied field. This reduces the field experienced at the nucleus.The electrons are said to shield the proton, an effect that is exactly dependent on the distance of the center. In addition, S-NICS can find the most accurate places for effective points for calculation of isotropy as an aromaticity criterion. The chemical shielding is a vector orientation function for all of the shielding parameters that can change in various places inside the shielding area of the rings for aromatic compounds.

The asymmetric (η),skew(k)parameters have frequent changing or fluctuatingvalues which have been modeled by a Gaussian distribution. And the shielding space around the center of benzene, naphthalene and borazine are canonical , where the (+) denotes the shielding and (–) indicates deshielding areas, and anisotropy as an orientation function has a fluctuating behavior and their values have been changed statistically in a Gaussian distribution.

On the other hand, the nearby protons will experience three fields:  the applied field, the shielding field of the valence electrons and the field due to the π systems. So field lines opposed to the applied field cause a reduced field in this area equivalent to shielding, anisotropic induced magnetic field lines due to the induced circulation of the π electron in the ring area of benzene, naphthalene and borazine.S-NICS hasbeen investigated by the Monte Carlo model by computation of nucleus-independent chemical shifts in many points of shielding areas around the rings of borazine, benzene and naphthalene, by choosing specified and suitable distances (Scheme 3).The statistical simulation by the Monte Carlo method is the generation of pseudo-random numbers that are distributed in a Gaussian distribution, and the algorithm is based on a pseudorandom number generator that produces numbers x that are uniformly distributed in the interval [0, 1).

These random varietiesx are then transformed via some algorithm to create a new random variate having the required probability distribution, (Tables 1, 2). The asymmetry (η), and skew (κ) parameters fluctuate by the changing of tensors, while in the case of an axially symmetric tensor, σ₂₂ equals either σ₁₁ or σ₃₃ and a = Ω/3, the span is κ= ±1 by changing asymmetry between 0 ≤ η ≤ +1.

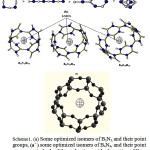Scheme1: (a) Some optimized isomers of B3N3, and their point groups, (aˊ ) some optimized isomers of B4N4, and their point groups, in both of them, the rings with alternation of B and N are more stable and the arrangements of stability are shown. (b) The sphere region of S-NICS in optimized structures of B12N12, B15N15 and B18N18 Rings .all molecules are optimized with B3LYP/EPR-II level.(C)The sphere region of S-NICS in optimized structures ofSi18O27 Click here to View Scheme

 

Table 1: The NMR Parameters for BQ=0/09(3)

B3LYP/6-31G    NMR=GIAO       0/09(3)
atom	σ11	σ22	σ33	∆σ	ƞ	σ0iso(2)	σ±2sym(2)	Span(Ω)	ƙ	σiso	ζzz
1	-956.9445	1083.4728	7532.725	7469.4609	0.4097519	6098.5658	2489.8203	8489.6695	0.5193176	2553.0844	4979.6406
2	-3374.1985	848.4266	5337.8656	6600.7516	0.9595783	5389.2937	2200.2506	8712.0641	0.0306258	937.36457	4400.5011
3	178.9333	744.1915	3142.4491	2680.8867	0.3162712	2188.8546	893.6289	2963.5158	0.6185219	1355.1913	1787.2578
4	-1183.6157	-469.2794	6653.7304	7480.178	0.1432459	6107.316	2493.3927	7837.3461	0.8177096	1666.9451	4986.7853
5	110.992	975.0664	12561.8095	12018.78	0.1078405	9812.9335	4006.2601	12450.818	0.861202	4549.2893	8012.5202
6	-367.8772	16.3726	2243.4669	2419.2192	0.2382482	1975.2118	806.4064	2611.3441	0.7057073	630.6541	1612.8128
7	-2763.2793	159.7606	5052.1679	6353.9273	0.6900551	5187.7698	2117.9758	7815.4472	0.251984	816.2164	4235.9515
8	-6289.8512	187.4013	2580.0565	5631.2815	1.7253406	4597.7536	1877.0938	8869.9077	-0.460501	-1174.131	3754.1876
9	-2148.2802	477.4417	2876.8497	3712.269	1.0609638	3030.9439	1237.423	5025.1299	-0.045036	402.00373	2474.846
10	-6512.5485	7.9388	2252.0367	5504.3416	1.7769121	4494.1115	1834.7806	8764.5852	-0.487917	-1417.524	3669.5611
11	-42.9918	220.3325	4828.4089	4739.7386	0.0833351	3869.8385	1579.9129	4871.4007	0.8918897	1668.5832	3159.8257
12	-4147.0372	-106.0939	4209.0304	6335.596	0.9567237	5172.8029	2111.8653	8356.0676	0.0328122	-14.70023	4223.7306
13	117.3647	419.4482	8906.534	8638.1276	0.0524564	7052.7432	2879.3759	8789.1693	0.9312601	3147.7823	5758.7517
14	-794.9836	459.2989	1653.8328	1821.6752	1.0327987	1487.337	607.22505	2448.8164	-0.024399	439.3827	1214.4501
15	-1318.8868	852.2523	8128.2713	8361.5886	0.3894844	6826.9584	2787.1962	9447.1581	0.5403614	2553.8789	5574.3924
16	-4035.1798	216.586	3860.1255	5769.4224	1.1054224	4710.5411	1923.1408	7895.3053	-0.077036	13.8439	3846.2816
17	-3007.5149	557.9322	1705.0616	2929.853	1.8254058	2392.1273	976.61765	4712.5765	-0.513163	-248.1737	1953.2353
18	-2652.2661	200.5141	3365.2841	4591.1601	0.9320455	3748.5292	1530.3867	6017.5502	0.0518466	304.5107	3060.7734
19	-1172.0822	1262.6031	7679.6091	7634.3487	0.478368	6233.1912	2544.7829	8851.6913	0.4498938	2590.0433	5089.5658
20	-844.0735	1466.732	7313.6022	7002.273	0.4950119	5717.1225	2334.091	8157.6757	0.4334647	2645.4202	4668.182
21	-132.9882	742.4337	2027.6005	1722.8778	0.7621741	1406.6723	574.2926	2160.5887	0.189645	879.01533	1148.5852
22	134.332	752.8564	2813.5901	2369.9959	0.3914718	1935.0227	789.99865	2679.2581	0.5382868	1233.5928	1579.9973
23	-1619.9856	1199.4706	5526.3823	5736.6398	0.7372233	4683.7751	1912.2133	7146.3679	0.2109401	1701.9558	3824.4265
24	-347.6019	1091.5889	10841.9332	10469.94	0.206189	8548.3568	3489.9799	11189.535	0.7427613	3861.9734	6979.9598
25	66.743	1106.2361	10142.7306	9556.2411	0.1631645	7802.3523	3185.4137	10075.988	0.7936692	3771.9032	6370.8274
26	-1552.0935	1098.0741	6058.0436	6285.0533	0.6324929	5131.5365	2095.0178	7610.1371	0.3035165	1868.0081	4190.0355
27	-4379.5365	5.4372	3699.8494	5886.8991	1.1173048	4806.4569	1962.2997	8079.3859	-0.085472	-224.75	3924.5994
28	-4706.3136	297.386	6313.2225	8517.6863	0.8811723	6954.4069	2839.2288	11019.536	0.0918493	634.76497	5678.4575
29	-5750.8297	150.5728	5251.3484	8051.4769	1.0994385	6573.7624	2683.8256	11002.178	-0.07277	-116.3028	5367.6512
30	-3377.6973	68.9263	1923.1441	3577.5296	1.4451132	2920.9336	1192.5099	5300.8414	-0.300406	-461.8756	2385.0197
31	-2529.0503	415.9993	2861.8965	3918.422	1.1273861	3199.2609	1306.1407	5390.9468	-0.092591	249.61517	2612.2813
32	-13313.7769	236.7772	6478.223	13016.723	1.5615168	10627.72	4338.9076	19792	-0.369296	-2199.592	8677.8152
33	-342.1912	-59.7532	3910.972	4111.9442	0.1030308	3357.2653	1370.6481	4253.1632	0.8671869	1169.6759	2741.2961
34	105.1833	260.4736	4135.8266	3952.9982	0.0589263	3227.4912	1317.6661	4030.6433	0.9229452	1500.4945	2635.3321
35	-8181.1451	-77.0719	2897.3435	7026.452	1.7300495	5736.8638	2342.1507	11078.489	-0.463029	-1786.958	4684.3013
36	-122.1222	-6.8953	7541.5657	7606.0745	0.022724	6210.1063	2535.3582	7663.6879	0.9699291	2470.8494	5070.7163
37	73.7637	445.2708	8317.0012	8057.484	0.0691606	6578.6671	2685.828	8243.2375	0.9098638	2945.3452	5371.656
38	-2371.0975	638.6244	6844.6029	7710.8395	0.5854853	6295.6433	2570.2798	9215.7004	0.3468273	1704.0433	5140.5596
39	-1705.6132	815.6228	7552.004	7996.9992	0.4729091	6529.2833	2665.6664	9257.6172	0.4553164	2220.6712	5331.3328
40	-3476.9414	273.655	867.2673	2468.9105	2.2786952	2015.7831	822.97015	4344.2087	-0.726711	-778.673	1645.9403
41	-3289.9488	414.833	1998.3208	3435.8787	1.6173949	2805.2804	1145.2929	5288.2696	-0.401132	-292.265	2290.5858
42	-1793.8273	-205.034	2362.3919	3361.8226	0.7088982	2744.816	1120.6075	4156.2192	0.2354622	121.17687	2241.215
43	-4159.9595	141.0963	6540.979	8550.4106	0.754535	6981.1253	2850.1369	10700.939	0.1961348	840.70527	5700.2738
44	-5750.4931	236.0481	5858.1423	8615.3648	1.042302	7034.1581	2871.7883	11608.635	-0.031394	114.56577	5743.5765
45	-11729.9838	133.1489	9979.1707	15777.588	1.1278466	12881.875	5259.1961	21709.155	-0.092915	-539.2214	10518.392
46	-1.2686	0.3899	60.9549	61.39425	0.0405209	50.126359	20.46475	62.2235	0.9466922	20.0254	40.9295

 

Table 2: The NMR Parameters for BQ=0.1(1)

B3LYP/6-31G    NMR=GIAO       0/1(1)
atom	σ11	σ22	σ33	∆σ	ƞ	σ0iso(2)	σ±2sym(2)	Span(Ω)	ƙ	σiso	ζzz
1	-956.9445	1083.4728	7532.725	7469.4609	0.4097519	6098.5658	2489.8203	8489.6695	0.5193176	2553.0844	4979.6406
2	-3374.1985	848.4266	5337.8656	6600.7516	0.9595783	5389.2937	2200.2506	8712.0641	0.0306258	937.36457	4400.5011
3	178.9333	744.1915	3142.4491	2680.8867	0.3162712	2188.8546	893.6289	2963.5158	0.6185219	1355.1913	1787.2578
4	-1183.6157	-469.2794	6653.7304	7480.178	0.1432459	6107.316	2493.3927	7837.3461	0.8177096	1666.9451	4986.7853
5	110.992	975.0664	12561.8095	12018.78	0.1078405	9812.9335	4006.2601	12450.818	0.861202	4549.2893	8012.5202
6	-367.8772	16.3726	2243.4669	2419.2192	0.2382482	1975.2118	806.4064	2611.3441	0.7057073	630.6541	1612.8128
7	-2763.2793	159.7606	5052.1679	6353.9273	0.6900551	5187.7698	2117.9758	7815.4472	0.251984	816.2164	4235.9515
8	-6289.8512	187.4013	2580.0565	5631.2815	1.7253406	4597.7536	1877.0938	8869.9077	-0.460501	-1174.131	3754.1876
9	-2148.2802	477.4417	2876.8497	3712.269	1.0609638	3030.9439	1237.423	5025.1299	-0.045036	402.00373	2474.846
10	-6512.5485	7.9388	2252.0367	5504.3416	1.7769121	4494.1115	1834.7806	8764.5852	-0.487917	-1417.524	3669.5611
11	-42.9918	220.3325	4828.4089	4739.7386	0.0833351	3869.8385	1579.9129	4871.4007	0.8918897	1668.5832	3159.8257
12	-4147.0372	-106.0939	4209.0304	6335.596	0.9567237	5172.8029	2111.8653	8356.0676	0.0328122	-14.70023	4223.7306
13	117.3647	419.4482	8906.534	8638.1276	0.0524564	7052.7432	2879.3759	8789.1693	0.9312601	3147.7823	5758.7517
14	-794.9836	459.2989	1653.8328	1821.6752	1.0327987	1487.337	607.22505	2448.8164	-0.024399	439.3827	1214.4501
15	-1318.8868	852.2523	8128.2713	8361.5886	0.3894844	6826.9584	2787.1962	9447.1581	0.5403614	2553.8789	5574.3924
16	-4035.1798	216.586	3860.1255	5769.4224	1.1054224	4710.5411	1923.1408	7895.3053	-0.077036	13.8439	3846.2816
17	-3007.5149	557.9322	1705.0616	2929.853	1.8254058	2392.1273	976.61765	4712.5765	-0.513163	-248.1737	1953.2353
18	-2652.2661	200.5141	3365.2841	4591.1601	0.9320455	3748.5292	1530.3867	6017.5502	0.0518466	304.5107	3060.7734
19	-1172.0822	1262.6031	7679.6091	7634.3487	0.478368	6233.1912	2544.7829	8851.6913	0.4498938	2590.0433	5089.5658
20	-844.0735	1466.732	7313.6022	7002.273	0.4950119	5717.1225	2334.091	8157.6757	0.4334647	2645.4202	4668.182
21	-132.9882	742.4337	2027.6005	1722.8778	0.7621741	1406.6723	574.2926	2160.5887	0.189645	879.01533	1148.5852
22	134.332	752.8564	2813.5901	2369.9959	0.3914718	1935.0227	789.99865	2679.2581	0.5382868	1233.5928	1579.9973
23	-1619.9856	1199.4706	5526.3823	5736.6398	0.7372233	4683.7751	1912.2133	7146.3679	0.2109401	1701.9558	3824.4265
24	-347.6019	1091.5889	10841.9332	10469.94	0.206189	8548.3568	3489.9799	11189.535	0.7427613	3861.9734	6979.9598
25	66.743	1106.2361	10142.7306	9556.2411	0.1631645	7802.3523	3185.4137	10075.988	0.7936692	3771.9032	6370.8274
26	-1552.0935	1098.0741	6058.0436	6285.0533	0.6324929	5131.5365	2095.0178	7610.1371	0.3035165	1868.0081	4190.0355
27	-4379.5365	5.4372	3699.8494	5886.8991	1.1173048	4806.4569	1962.2997	8079.3859	-0.085472	-224.75	3924.5994
28	-4706.3136	297.386	6313.2225	8517.6863	0.8811723	6954.4069	2839.2288	11019.536	0.0918493	634.76497	5678.4575
29	-5750.8297	150.5728	5251.3484	8051.4769	1.0994385	6573.7624	2683.8256	11002.178	-0.07277	-116.3028	5367.6512
30	-3377.6973	68.9263	1923.1441	3577.5296	1.4451132	2920.9336	1192.5099	5300.8414	-0.300406	-461.8756	2385.0197
31	-2529.0503	415.9993	2861.8965	3918.422	1.1273861	3199.2609	1306.1407	5390.9468	-0.092591	249.61517	2612.2813
32	-13313.7769	236.7772	6478.223	13016.723	1.5615168	10627.72	4338.9076	19792	-0.369296	-2199.592	8677.8152
33	-342.1912	-59.7532	3910.972	4111.9442	0.1030308	3357.2653	1370.6481	4253.1632	0.8671869	1169.6759	2741.2961
34	105.1833	260.4736	4135.8266	3952.9982	0.0589263	3227.4912	1317.6661	4030.6433	0.9229452	1500.4945	2635.3321
35	-8181.1451	-77.0719	2897.3435	7026.452	1.7300495	5736.8638	2342.1507	11078.489	-0.463029	-1786.958	4684.3013
36	-122.1222	-6.8953	7541.5657	7606.0745	0.022724	6210.1063	2535.3582	7663.6879	0.9699291	2470.8494	5070.7163
37	73.7637	445.2708	8317.0012	8057.484	0.0691606	6578.6671	2685.828	8243.2375	0.9098638	2945.3452	5371.656
38	-2371.0975	638.6244	6844.6029	7710.8395	0.5854853	6295.6433	2570.2798	9215.7004	0.3468273	1704.0433	5140.5596
39	-1705.6132	815.6228	7552.004	7996.9992	0.4729091	6529.2833	2665.6664	9257.6172	0.4553164	2220.6712	5331.3328
40	-3476.9414	273.655	867.2673	2468.9105	2.2786952	2015.7831	822.97015	4344.2087	-0.726711	-778.673	1645.9403
41	-3289.9488	414.833	1998.3208	3435.8787	1.6173949	2805.2804	1145.2929	5288.2696	-0.401132	-292.265	2290.5858
42	-1793.8273	-205.034	2362.3919	3361.8226	0.7088982	2744.816	1120.6075	4156.2192	0.2354622	121.17687	2241.215
43	-4159.9595	141.0963	6540.979	8550.4106	0.754535	6981.1253	2850.1369	10700.939	0.1961348	840.70527	5700.2738
44	-5750.4931	236.0481	5858.1423	8615.3648	1.042302	7034.1581	2871.7883	11608.635	-0.031394	114.56577	5743.5765
45	-11729.9838	133.1489	9979.1707	15777.588	1.1278466	12881.875	5259.1961	21709.155	-0.092915	-539.2214	10518.392

 

Table 3: The NMR Parameter for BQ=0/1(2)

B3LYP/6-31G    NMR=GIAO       0/1(2)
atom	σ11	σ22	σ33	∆σ	ƞ	σ0iso(2)	σ±sym(2)	Span(Ω)	ƙ	σiso	ζzz
1	-956.9445	1083.4728	7532.725	7469.4609	0.4097519	6098.5658	2489.8203	8489.6695	0.5193176	2553.0844	4979.6406
2	-3374.1985	848.4266	5337.8656	6600.7516	0.9595783	5389.2937	2200.2506	8712.0641	0.0306258	937.36457	4400.5011
3	178.9333	744.1915	3142.4491	2680.8867	0.3162712	2188.8546	893.6289	2963.5158	0.6185219	1355.1913	1787.2578
4	-1183.6157	-469.2794	6653.7304	7480.178	0.1432459	6107.316	2493.3927	7837.3461	0.8177096	1666.9451	4986.7853
5	110.992	975.0664	12561.8095	12018.78	0.1078405	9812.9335	4006.2601	12450.818	0.861202	4549.2893	8012.5202
6	-367.8772	16.3726	2243.4669	2419.2192	0.2382482	1975.2118	806.4064	2611.3441	0.7057073	630.6541	1612.8128
7	-2763.2793	159.7606	5052.1679	6353.9273	0.6900551	5187.7698	2117.9758	7815.4472	0.251984	816.2164	4235.9515
8	-6289.8512	187.4013	2580.0565	5631.2815	1.7253406	4597.7536	1877.0938	8869.9077	-0.460501	-1174.131	3754.1876
9	-2148.2802	477.4417	2876.8497	3712.269	1.0609638	3030.9439	1237.423	5025.1299	-0.045036	402.00373	2474.846
10	-6512.5485	7.9388	2252.0367	5504.3416	1.7769121	4494.1115	1834.7806	8764.5852	-0.487917	-1417.524	3669.5611
11	-42.9918	220.3325	4828.4089	4739.7386	0.0833351	3869.8385	1579.9129	4871.4007	0.8918897	1668.5832	3159.8257
12	-4147.0372	-106.0939	4209.0304	6335.596	0.9567237	5172.8029	2111.8653	8356.0676	0.0328122	-14.70023	4223.7306
13	117.3647	419.4482	8906.534	8638.1276	0.0524564	7052.7432	2879.3759	8789.1693	0.9312601	3147.7823	5758.7517
14	-794.9836	459.2989	1653.8328	1821.6752	1.0327987	1487.337	607.22505	2448.8164	-0.024399	439.3827	1214.4501
15	-1318.8868	852.2523	8128.2713	8361.5886	0.3894844	6826.9584	2787.1962	9447.1581	0.5403614	2553.8789	5574.3924
16	-4035.1798	216.586	3860.1255	5769.4224	1.1054224	4710.5411	1923.1408	7895.3053	-0.077036	13.8439	3846.2816
17	-3007.5149	557.9322	1705.0616	2929.853	1.8254058	2392.1273	976.61765	4712.5765	-0.513163	-248.1737	1953.2353
18	-2652.2661	200.5141	3365.2841	4591.1601	0.9320455	3748.5292	1530.3867	6017.5502	0.0518466	304.5107	3060.7734
19	-1172.0822	1262.6031	7679.6091	7634.3487	0.478368	6233.1912	2544.7829	8851.6913	0.4498938	2590.0433	5089.5658
20	-844.0735	1466.732	7313.6022	7002.273	0.4950119	5717.1225	2334.091	8157.6757	0.4334647	2645.4202	4668.182
21	-132.9882	742.4337	2027.6005	1722.8778	0.7621741	1406.6723	574.2926	2160.5887	0.189645	879.01533	1148.5852
22	134.332	752.8564	2813.5901	2369.9959	0.3914718	1935.0227	789.99865	2679.2581	0.5382868	1233.5928	1579.9973
23	-1619.9856	1199.4706	5526.3823	5736.6398	0.7372233	4683.7751	1912.2133	7146.3679	0.2109401	1701.9558	3824.4265
24	-347.6019	1091.5889	10841.9332	10469.94	0.206189	8548.3568	3489.9799	11189.535	0.7427613	3861.9734	6979.9598
25	66.743	1106.2361	10142.7306	9556.2411	0.1631645	7802.3523	3185.4137	10075.988	0.7936692	3771.9032	6370.8274
26	-1552.0935	1098.0741	6058.0436	6285.0533	0.6324929	5131.5365	2095.0178	7610.1371	0.3035165	1868.0081	4190.0355
27	-4379.5365	5.4372	3699.8494	5886.8991	1.1173048	4806.4569	1962.2997	8079.3859	-0.085472	-224.75	3924.5994
28	-4706.3136	297.386	6313.2225	8517.6863	0.8811723	6954.4069	2839.2288	11019.536	0.0918493	634.76497	5678.4575
29	-5750.8297	150.5728	5251.3484	8051.4769	1.0994385	6573.7624	2683.8256	11002.178	-0.07277	-116.3028	5367.6512
30	-3377.6973	68.9263	1923.1441	3577.5296	1.4451132	2920.9336	1192.5099	5300.8414	-0.300406	-461.8756	2385.0197
31	-2529.0503	415.9993	2861.8965	3918.422	1.1273861	3199.2609	1306.1407	5390.9468	-0.092591	249.61517	2612.2813
32	-13313.7769	236.7772	6478.223	13016.723	1.5615168	10627.72	4338.9076	19792	-0.369296	-2199.592	8677.8152
33	-342.1912	-59.7532	3910.972	4111.9442	0.1030308	3357.2653	1370.6481	4253.1632	0.8671869	1169.6759	2741.2961
34	105.1833	260.4736	4135.8266	3952.9982	0.0589263	3227.4912	1317.6661	4030.6433	0.9229452	1500.4945	2635.3321
35	-8181.1451	-77.0719	2897.3435	7026.452	1.7300495	5736.8638	2342.1507	11078.489	-0.463029	-1786.958	4684.3013
36	-122.1222	-6.8953	7541.5657	7606.0745	0.022724	6210.1063	2535.3582	7663.6879	0.9699291	2470.8494	5070.7163
37	73.7637	445.2708	8317.0012	8057.484	0.0691606	6578.6671	2685.828	8243.2375	0.9098638	2945.3452	5371.656
38	-2371.0975	638.6244	6844.6029	7710.8395	0.5854853	6295.6433	2570.2798	9215.7004	0.3468273	1704.0433	5140.5596
39	-1705.6132	815.6228	7552.004	7996.9992	0.4729091	6529.2833	2665.6664	9257.6172	0.4553164	2220.6712	5331.3328
40	-3476.9414	273.655	867.2673	2468.9105	2.2786952	2015.7831	822.97015	4344.2087	-0.726711	-778.673	1645.9403
41	-3289.9488	414.833	1998.3208	3435.8787	1.6173949	2805.2804	1145.2929	5288.2696	-0.401132	-292.265	2290.5858
42	-1793.8273	-205.034	2362.3919	3361.8226	0.7088982	2744.816	1120.6075	4156.2192	0.2354622	121.17687	2241.215
43	-4159.9595	141.0963	6540.979	8550.4106	0.754535	6981.1253	2850.1369	10700.939	0.1961348	840.70527	5700.2738
44	-5750.4931	236.0481	5858.1423	8615.3648	1.042302	7034.1581	2871.7883	11608.635	-0.031394	114.56577	5743.5765
45	-11729.9838	133.1489	9979.1707	15777.588	1.1278466	12881.875	5259.1961	21709.155	-0.092915	-539.2214	10518.392
46	-1.4025	0.303	60.591	61.14075	0.041842	49.919384	20.38025	61.9935	0.9449781	19.8305	40.7605

 

Table 4: The NMR Parameter for BQ=0/1(3)

B3LYP/6-31G    NMR=GIAO       0/1(3)
	σ11	σ22	σ33	∆σ	ƞ	σ0iso(2)	σ±sym(2)	Span(Ω)	ƙ	σiso	ζzz
1	-956.9445	1083.4728	7532.725	7469.4609	0.4097519	6098.5658	2489.8203	8489.6695	0.5193176	2553.0844	4979.6406
2	-3374.1985	848.4266	5337.8656	6600.7516	0.9595783	5389.2937	2200.2506	8712.0641	0.0306258	937.36457	4400.5011
3	178.9333	744.1915	3142.4491	2680.8867	0.3162712	2188.8546	893.6289	2963.5158	0.6185219	1355.1913	1787.2578
4	-1183.6157	-469.2794	6653.7304	7480.178	0.1432459	6107.316	2493.3927	7837.3461	0.8177096	1666.9451	4986.7853
5	110.992	975.0664	12561.8095	12018.78	0.1078405	9812.9335	4006.2601	12450.818	0.861202	4549.2893	8012.5202
6	-367.8772	16.3726	2243.4669	2419.2192	0.2382482	1975.2118	806.4064	2611.3441	0.7057073	630.6541	1612.8128
7	-2763.2793	159.7606	5052.1679	6353.9273	0.6900551	5187.7698	2117.9758	7815.4472	0.251984	816.2164	4235.9515
8	-6289.8512	187.4013	2580.0565	5631.2815	1.7253406	4597.7536	1877.0938	8869.9077	-0.460501	-1174.131	3754.1876
9	-2148.2802	477.4417	2876.8497	3712.269	1.0609638	3030.9439	1237.423	5025.1299	-0.045036	402.00373	2474.846
10	-6512.5485	7.9388	2252.0367	5504.3416	1.7769121	4494.1115	1834.7806	8764.5852	-0.487917	-1417.524	3669.5611
11	-42.9918	220.3325	4828.4089	4739.7386	0.0833351	3869.8385	1579.9129	4871.4007	0.8918897	1668.5832	3159.8257
12	-4147.0372	-106.0939	4209.0304	6335.596	0.9567237	5172.8029	2111.8653	8356.0676	0.0328122	-14.70023	4223.7306
13	117.3647	419.4482	8906.534	8638.1276	0.0524564	7052.7432	2879.3759	8789.1693	0.9312601	3147.7823	5758.7517
14	-794.9836	459.2989	1653.8328	1821.6752	1.0327987	1487.337	607.22505	2448.8164	-0.024399	439.3827	1214.4501
15	-1318.8868	852.2523	8128.2713	8361.5886	0.3894844	6826.9584	2787.1962	9447.1581	0.5403614	2553.8789	5574.3924
16	-4035.1798	216.586	3860.1255	5769.4224	1.1054224	4710.5411	1923.1408	7895.3053	-0.077036	13.8439	3846.2816
17	-3007.5149	557.9322	1705.0616	2929.853	1.8254058	2392.1273	976.61765	4712.5765	-0.513163	-248.1737	1953.2353
18	-2652.2661	200.5141	3365.2841	4591.1601	0.9320455	3748.5292	1530.3867	6017.5502	0.0518466	304.5107	3060.7734
19	-1172.0822	1262.6031	7679.6091	7634.3487	0.478368	6233.1912	2544.7829	8851.6913	0.4498938	2590.0433	5089.5658
20	-844.0735	1466.732	7313.6022	7002.273	0.4950119	5717.1225	2334.091	8157.6757	0.4334647	2645.4202	4668.182
21	-132.9882	742.4337	2027.6005	1722.8778	0.7621741	1406.6723	574.2926	2160.5887	0.189645	879.01533	1148.5852
22	134.332	752.8564	2813.5901	2369.9959	0.3914718	1935.0227	789.99865	2679.2581	0.5382868	1233.5928	1579.9973
23	-1619.9856	1199.4706	5526.3823	5736.6398	0.7372233	4683.7751	1912.2133	7146.3679	0.2109401	1701.9558	3824.4265
24	-347.6019	1091.5889	10841.9332	10469.94	0.206189	8548.3568	3489.9799	11189.535	0.7427613	3861.9734	6979.9598
25	66.743	1106.2361	10142.7306	9556.2411	0.1631645	7802.3523	3185.4137	10075.988	0.7936692	3771.9032	6370.8274
26	-1552.0935	1098.0741	6058.0436	6285.0533	0.6324929	5131.5365	2095.0178	7610.1371	0.3035165	1868.0081	4190.0355
27	-4379.5365	5.4372	3699.8494	5886.8991	1.1173048	4806.4569	1962.2997	8079.3859	-0.085472	-224.75	3924.5994
28	-4706.3136	297.386	6313.2225	8517.6863	0.8811723	6954.4069	2839.2288	11019.536	0.0918493	634.76497	5678.4575
29	-5750.8297	150.5728	5251.3484	8051.4769	1.0994385	6573.7624	2683.8256	11002.178	-0.07277	-116.3028	5367.6512
30	-3377.6973	68.9263	1923.1441	3577.5296	1.4451132	2920.9336	1192.5099	5300.8414	-0.300406	-461.8756	2385.0197
31	-2529.0503	415.9993	2861.8965	3918.422	1.1273861	3199.2609	1306.1407	5390.9468	-0.092591	249.61517	2612.2813
32	-13313.7769	236.7772	6478.223	13016.723	1.5615168	10627.72	4338.9076	19792	-0.369296	-2199.592	8677.8152
33	-342.1912	-59.7532	3910.972	4111.9442	0.1030308	3357.2653	1370.6481	4253.1632	0.8671869	1169.6759	2741.2961
34	105.1833	260.4736	4135.8266	3952.9982	0.0589263	3227.4912	1317.6661	4030.6433	0.9229452	1500.4945	2635.3321
35	-8181.1451	-77.0719	2897.3435	7026.452	1.7300495	5736.8638	2342.1507	11078.489	-0.463029	-1786.958	4684.3013
36	-122.1222	-6.8953	7541.5657	7606.0745	0.022724	6210.1063	2535.3582	7663.6879	0.9699291	2470.8494	5070.7163
37	73.7637	445.2708	8317.0012	8057.484	0.0691606	6578.6671	2685.828	8243.2375	0.9098638	2945.3452	5371.656
38	-2371.0975	638.6244	6844.6029	7710.8395	0.5854853	6295.6433	2570.2798	9215.7004	0.3468273	1704.0433	5140.5596
39	-1705.6132	815.6228	7552.004	7996.9992	0.4729091	6529.2833	2665.6664	9257.6172	0.4553164	2220.6712	5331.3328
40	-3476.9414	273.655	867.2673	2468.9105	2.2786952	2015.7831	822.97015	4344.2087	-0.726711	-778.673	1645.9403
41	-3289.9488	414.833	1998.3208	3435.8787	1.6173949	2805.2804	1145.2929	5288.2696	-0.401132	-292.265	2290.5858
42	-1793.8273	-205.034	2362.3919	3361.8226	0.7088982	2744.816	1120.6075	4156.2192	0.2354622	121.17687	2241.215
43	-4159.9595	141.0963	6540.979	8550.4106	0.754535	6981.1253	2850.1369	10700.939	0.1961348	840.70527	5700.2738
44	-5750.4931	236.0481	5858.1423	8615.3648	1.042302	7034.1581	2871.7883	11608.635	-0.031394	114.56577	5743.5765
45	-11729.9838	133.1489	9979.1707	15777.588	1.1278466	12881.875	5259.1961	21709.155	-0.092915	-539.2214	10518.392
46	-1.2697	0.3822	60.9302	61.37395	0.040373	50.109825	20.458	62.1999	0.9468826	20.014233	40.916

 

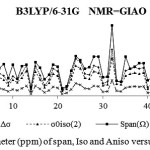Figure 1: NMR Parameter (ppm) of span, Iso and Aniso versus atomic number Click here to View Figure

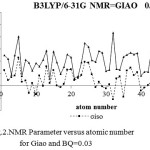Figure 2: NMR Parameter versus atomic number for Giao and BQ=0.03 Click here to View Figure

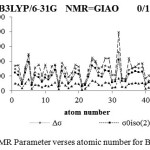Figure 3: NMR Parameter verses atomic number for BQ=0.1 Click here to View Figure

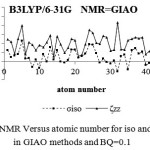Figure 4: NMR Versus atomic number for iso and ZZ in GIAO methods and BQ=0.1 Click here to View Figure

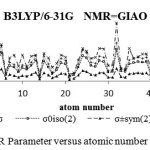Figure 5: NMR Parameter versus atomic number  for Span Click here to View Figure

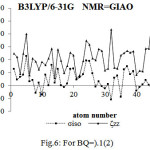Figure 6: For BQ=).1(2) Click here to View Figure

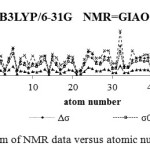Figure 7: ppm of NMR data versus atomic number Click here to View Figure

Figure 8: ZigmaIso for the Giao=0.1(3)  Click here to View Figure

 

References

1. Minkin, V. J. ;Glukhovtsev, M. N. ;Simkin, B.Y. ;Electronic and Structural Aspects, Wiley, New York, 1984.
2. Mason, J. ;Solid State Nucl.Magn.Reson.1993,2, 285.
3. Schleyer, P. v. R. ; Jiao, H. ; van EikemaHommes, N. J. R. ;Malkin, V. G. ;Malkina, O. L. ; J. Am. Chem. Soc. 1997, 119, 12669.
4. Schleyer, P. v. R. ;Maerker, C. ;Dransfeld, A. ; Jiao, H. ; van EikemaHommes, N. J. R.  J. Am. Chem.Soc.1996,118, 6317.
5. Schleyer, P. v. R. ; Jiao, H. ;Pure. Appl. Chem.1996, 68, 209.
6. Kruszewski, J .; Krygowski, T. M. ;Tetrahedron Letters,1972,36, 3839.
7. Stepien, B.T. ;Krygowski, T.M. ;Cyranski, M.K. ;Mlochowski, J.;Orioli, P. ;Abbate, F.  ARKIVOC,2004, 3,185.
8. Katritzky, A. R. ; Barczynski, P.;Musumarra, G. ; Pisano, D. ;Szafran, M.  J. Am. Chem.Soc.1989, 111, 7.
9. Feixas, F. ;Matito, E. ;Poater, J. ;Solà, M.  Journal of Computational Chemistry.2008, 29, 543.
10. Katritzky, A. R.;Karelson,  M.;Sild, S.;Krygowski, T. M.;  Jug. K.  J. Org. Chem.1998,63, 5228.
11. Fias, S.; Van Damme, S.; Bultinck,P.; Journal of Computational Chemistry. 2008,29, 358.
12. Hehre, W. J.  R.;Ditchfield, Radom, L.;Pople, J. A.  J. Am. Chem. Soc.1970, 92, 4796.
13. Cooper, D. L.;Gerratt, J.;  Raimondi, M.  Nature,1986,323, 699.
14. Julg, A. Francois, Ph.;Theor. Chim.Acta.1967,7, 249.
15. Monajjemi, M.;Struct. Chem.2012,23, 551.
16. Monajjemi, M.; Lee, V. S.;Khaleghian, M.;Honarparvar, B.;Mollaamin. F.;J. Phys. Chem. C.2010114, 15315.
17. Monajjemi, M.;Khaleghian, M.;J. Cluster Sci.2011, 22, 673.
18. Monajjemi, M.; Boggs, J.E, J. Phys. Chem. A,20133.
19. Frueh, D.;Nucl.P.;Reson.M,Spectrosc.2002,41, 305.
20. Jiao, H.;  .Schleyer, P. v. R,J. Am. Chem. Soc. 1995,117, 11529.
21. Martin, N. H.; Nance, K.H.;Journal of Molecular Graphics and Modelling.2002,21, 51.
22. Luginbhl, P.;Wuthrich , K.;Progress in Nuclear Magnetic Resonance Spectroscopy.2002, 40, 199.
23. Magn. R. L.;Reson. Rev.1987,12, 91.
24. Monajjemi,M.; Mohammadian,T.N.; J. Comput. Theor.Nanosci.2015, 12, 4895-4914.
25. Greenwood, Norman N.; Earnshaw, Alan Chemistry of the Elements (2nd ed.). Butterworth-Heinemann.(1997). ISBN 0080379419.
26. Laurent, S.; Forge, D.; Port, M.; Roch, A.; Robic, C.; Vander Elst, L.; Muller, R.N. Chem. Rev. 2008, 108, 2064–2110.
27. Kodama, R.H. Magnetic nanoparticles. J. Magn. Magn.Mater.1999, 200, 359–372.
28. Chang, L.L.; Erathodiyil, N.; Ying, J.Y. Acc. Chem. Res. 2012, 46, 1825–1837.
29. Fujishima, A.; Zhang, X.; Tryk, D.A. Surf. Sci. Rep. 2008, 63, 515–582.
30. Wang, X.; Starz-Gaiano, M.; Bridges, T.; Montell, D. Protoc, Exch,2008, 28.
31. Mahdavian, L.; Monajjemi, M. Microelectronics Journal. 2010,41(2-3), 142-149
32. Ali R. Ilkhani .; MajidMonajjemi, Computational and Theoretical Chemistry.2015, 1074 19–25
33. Monajjemi,M *.; Bagheri,S.; Moosavi,M.S..; Moradiyeh,N.; Zakeri,M.; Attarikhasraghi,N.; Saghayimarouf,N.; Niyatzadeh,G.; Shekarkhand,M.; Mohammad S. Khalilimofrad, Ahmadin,H.; Ahadi,M.; Molecules 2015, 20, 21636–21657;
34. Monajjemi, M., Chahkandi, B. Journal of Molecular Structure: THEOCHEM, 2005, 714 (1), 28, 43-60.
35. Monajjemi, M.; Rajaeian, E.; Mollaamin, F.; Naderi, F.; Saki, S. Physics and Chemistry of Liquids. 2008, 46 (3), 299-306
36. Monajjemi, M.;  Razavian, M.H.;  Mollaamin,F.;  Naderi,F.;  Honarparvar,B.; Russian Journal of Physical Chemistry A , 2008 , 82 (13),  2277-2285
37. Monajjemi, M. Chemical Physics. 2013, 425, 29-45
38. Monajjemi, M.; Ketabi, S.; Amiri, A. Russian Journal of Physical Chemistry, 2006, 80 (1), S55-S62
39. Monajjemi, M.; Wayne Jr, Robert. Boggs, J.E. Chemical Physics.2014, 433, 1-11
40. Monajjemi, M.; Honarparvar, B.; Nasseri, S. M. .; Khaleghian M. Journal of Structural Chemistry. 2009, 50, 1, 67-77
41. Ardalan, T.; Ardalan, P.; Monajjemi, M. Fullerenes, Nanotubes, and Carbon Nanostructures, 2014, 22: 687–708
42. Monajjemi, M.;  Karachi, N.; Mollaamin, F. Fullerenes, Nanotubes, and Carbon Nanostructures, 2014, 22: 643–662
43. Yahyaei, H.; Monajjemi, M. Fullerenes, Nanotubes, and Carbon Nanostructures.2014, 22(4), 346–361
44. Monajjemi, M. Falahati, M.; Mollaamin, F.; Ionics, 2013, 19, 155–164
45. Monajjemi, M.; Mollaamin, F. Journal of Cluster Science, 2012, 23(2), 259-272
46. Tahan, A.; Monajjemi, M. Acta Biotheor,2011, 59, 291–312
47. Lee, V.S.; Nimmanpipug, P.; Mollaamin, F.; Kungwan, N.; Thanasanvorakun, S..; Monajjemi, M.  Russian Journal of Physical Chemistry A, 2009,83, 13, 2288–2296
48. Monajjemi, M.; Heshmat, M.; Haeri, HH, Biochemistry (Moscow), 2006, 71 (1), S113-S122
49. Monajjemi, M.; JafariAzan, M.; Mollaamin, F. Fullerenes, Nanotubes, and Carbon Nanostructures.2013, 21(6), 503–515
50. Mollaamin, F.; Monajjemi, M.Physics and Chemistry of Liquids .2012, 50,  5,  2012, 596–604
51. Monajjemi, M.; Khosravi, M.; Honarparvar, B.; Mollaamin, F.; International Journal of Quantum Chemistry, 2011, 111, 2771–2777
52. Monajjemi, M.; Baheri, H.; Mollaamin, F.  Journal of Structural Chemistry.201152(1), 54-59
53. Mahdavian, L.; Monajjemi, M.; Mangkorntong, N. Fullerenes, Nanotubes and Carbon Nanostructures, 2009, 17 (5), 484-495
54. Monajjemi, M.; Farahani, N.; Mollaamin, F. Physics and Chemistry of Liquids, 2012, 50(2) 161–172
55. Monajjemi, M.  TheorChemAcc, 2015, 134:77 DOI 10.1007/s00214-015-1668-9
56. Monajjemi, M.  Journal of Molecular Modeling, 2014, 20, 2507
57. Monajjemi , M.; Honarparvar, B.; Monajemi, H.;.Journal of the Mexican Chemical Society, 2006, 50 (4), 143-148
58. Monajjemi, M.; Khaleghian, M.; Mollaamin, F.  Molecular Simulation. 2010, 36, 11,  865–
59. Monajjemi, M.  Biophysical Chemistry.2015207,114 –127
60. Sarasia, E.M.; Afsharnezhad, S.; Honarparvar, B.; Mollaamin, F.; Monajjemi, M. Physics and Chemistry of Liquids.2011, 49 (5), 561-571
61. Amiri, A.; Babaeie, F.; Monajjemi, M.Physics and Chemistry of Liquids. 2008, 46, 4, 379-389
62. Jalilian,H.; Monajjemi, M. Japanese Journal of Applied Physics. 2015,54, 8, 08510
63. Naghsh,F, orient.jchem,2015, 31(1) 465-478
64. Chitsazan, A, orient.jchem,2015, 31(1) 393- 408
65. Barmaki, Z, orient.jchem, 2015, 31(3) 1723-1733
66. Bonsakhteh, B.; Rustaiyan, A.H, orient.jchem, 2014, 30(4) 1703-1718

---

This work is licensed under a Creative Commons Attribution 4.0 International License.