Vibrational Frequencies of PH3 and NF3: Lie Algebraic Method
J. Vijayasekhar1*, K. Srinivasa Rao2 and B. V. S. N. Hari Prasad3
1Department of Mathematics, GITAM University, Hyderabad.
2Department of ECE, K L University, Vaddeswaram, Andhra Pradesh.
3Department of Mathematics, Dhanekula Institute of Engg. and Technology,Vijayawada.
Corresponding Author E-mail: vijayjaliparthi@gmail.com
DOI : http://dx.doi.org/10.13005/ojc/320352
Article Received on : May 30, 2016
Article Accepted on : June 17, 2016
The subject field of vibrational frequencies of polyatomic molecules is an interesting and innovative work in the field of molecular spectroscopy. In this paper we are concerned with the vibrational frequencies of Phosphine (PH3) and Nitrogen triflouride (NF3) using Lie algebraic method.
KEYWORDS:Vibrational spectra; Lie algebraic method
Download this article as:| Copy the following to cite this article: Vijayasekhar J, Rao K. S, Prasad B. V. S. N. H. Vibrational Frequencies of PH3 and NF3: Lie Algebraic Method. Orient J Chem 2016;32(3). |
| Copy the following to cite this URL: Vijayasekhar J, Rao K. S, Prasad B. V. S. N. H. Vibrational Frequencies of PH3 and NF3: Lie Algebraic Method. Orient J Chem 2016;32(3). Available from: http://www.orientjchem.org/?p=17868 |
Introduction
In the last part of the 19th century, Marius Sophus Lie proposed Lie algebras. Nevertheless, these methods have been useful in the study of the problems in the beginning portion of the 20th century, after the evaluation of quantum mechanics1, 2. Iachello (1981) presented Lie algebraic method (vibron model) for the study of vibrational spectra of molecules. This method is based on the second quantization of the Schrodinger wave equation with a 3- Dimensional Morse potential function and is described as ro-vibration spectra of diatomic molecules. Considerable attention has been given to determining vibration spectra of molecules. Therefore the study of molecular spectroscopy is fundamental to understanding both experimental and theoretical approaches. There are two general methods which are used to describe molecular vibrations. In the classical approach, the molecular Hamiltonian is parameterized in terms of internal coordinates and the potential energy function is represented in terms of force field constants by spectroscopic data. Although diatomic molecules have very accurate information on force fields, but not in the case of polyatomic molecules. The molecular rotation-vibration spectrum is provided by the Dunham expansion. It is a series of expansion of energy levels of rotational (J) and vibrational (v) quantum numbers. The constant coefficients yij are called Dunham parameters. For diatomic molecules, the expansion is
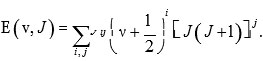
This approach is useful when the spectra can be expressed by a small number of parameters. The major drawbacks of this approach are that there is no Hamiltonian operator and it requires more number of parameters for large polyatomic molecules. The second approach is the potential approach. This approach is based on the Schrodinger wave equation. In this approach, the energy levels are computed by fitting the Schrodinger wave equation in terms of interatomic potential. The potential is expanded in terms of interatomic variable. For diatomic molecules, the possible expansion is
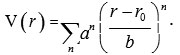
The potential coefficients, a’s are evaluated by fitting the experimental data on energy levels. The basic drawback of this approach is that it is very difficult to fit potential coefficients if the numbers of atoms are more in the molecule6. To overcome the difficulties raised in analysing the vibrational spectra, we consider the third approach (Lie algebraic method).
Lie Algebraic Method
The Hamiltonian in the case of stretching vibrations for the polyatomic is of the form 5
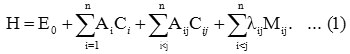
Here i vary from 1 to n for n stretching bonds and Ai , Aij and λij are algebraic parameters, which are determined by spectroscopic data. Where Ci is an invariant operator of the uncoupled bond with eigenvalue
![]()
and the operator Cij for coupled bonds are diagonal with matrix elements
![]()
while the Majorana operator Mij has both diagonal and non-diagonal matrix elements
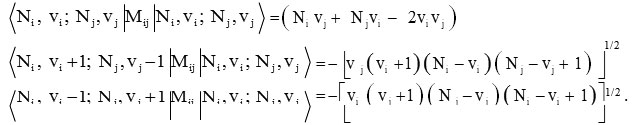
Where vi (i=1, 2, 3..) are vibrational quantum numbers. The vibron number for stretching bonds of molecule will be calculated by the following relation Ni (i =1, 2, 3.. )
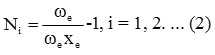
Here ωe and ωe xe are the spectroscopic constants. The initial guess value for the parameter Ai is obtained by using the energy equation for the single-oscillator fundamental mode, which is given as,
![]()
Initial guess for Aij may be taken as zero. The parameter λij obtained from the relation
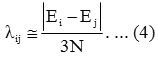
To have better results a numerical fitting procedure is required to obtain the parameters Ai , λii starting from values as given by Equations (3) and (4)3,4.
Results
Table 1: Vibrational spectra of PH3 and NF3
| Vibrational mode | Vibrational frequency (cm–1) | |
|
PH3 |
NF3 |
|
|
(1 0 0) |
2319.42356 | 1032.645 |
|
(2 0 0) |
4564.0573 | 2046.936 |
|
(3 0 0) |
6643.0241 | 2670.678 |
Table 2: Fitting parameters3, 4
| PH3 | NF3 |
| N=52Ai =-10.0456 Aij=-0.065 ëij=-0.0123 | N=140Ai =-2.43Aij= 0.07ëij=-0.332 |
Conclusion
In this paper we have reported the vibrational frequencies of PH3 and NF3 for three vibrational modes.
Acknowlwdgements
The author J. Vijayasekhar would like to thank K. Srinivasa Rao and Nirmal Kumar Sarkar for providing the necessary literature for this study.
References
- Iachello, F.; Oss S. J. Mol. Spectrosc. 1992, 153(1-2), 225-239.
CrossRef - Iachello, F.; Oss, S. Eur. J. Phys D. 2002, 19(3), 307-314.
- Choudhury, J.; Sarkar, N. K.; Bhattacharjee, R. Chin. Phys. Lett., 2013, 30(7), 070301(1-4).
- Karumuri, S. R.; Srinivas, G.; Vijayasekhar, J.; Sunil Babu, K.; S. S. Kumar, V.; Hanumaiah, A. Open Journal of Microphysics. 2013, 3, 47-51.
CrossRef - Oss, S. Adv. Chem. Phys. 1996, 93, 455-649.
- Karumuri, S. R.; Rao, V. U. M.; Vijayasekhar, J. Orient. J Chem. 2016, 32(1), 437-440.
CrossRef

This work is licensed under a Creative Commons Attribution 4.0 International License.









