ISSN : 0970 - 020X, ONLINE ISSN : 2231-5039
     FacebookTwitterLinkedinMendeley

Controller Performance Analysis for A Delayed Process Based on Integral Error Performance Indices

Volume 32, Number 3

Deeksha Naithani1, Mayank Chaturvedi2*and Pradeep Kumar Juneja3

1Department of Electrical Engineering.

2Department of Electronics and Communication Engineering3 Graphic Era University, Dehradun.

Corresponding Author E-mail ID: mayankchaturvedi.geit@gmail.com

 

DOI : http://dx.doi.org/10.13005/ojc/320344

Article Publishing History
Article Received on : May 28, 2016
Article Accepted on : June 25, 2016
Article Metrics
ABSTRACT:

In the present work, heat exchanger process is selected for investigation, which can be modelled as first order plus dead time model. PI controllers using various tuning techniques that are Ziegler-Nichols, Shinskey, Skogestad, Liptak and Moros have been designed for the selected process. Important time response characteristics and integral error performance indices viz. ISE, IAE and ITAE are calculated and compared to evaluate controller performance.

KEYWORDS:

Performance indices; Heat exchanger; dead time; FOPDT

Download this article as: 

Copy the following to cite this article:

Naithani D, Chaturvedi M, Juneja P. K. Controller Performance Analysis for A Delayed Process Based on Integral Error Performance Indices. Orient J Chem 2016;32(3).

Copy the following to cite this URL:

Naithani D, Chaturvedi M, Juneja P. K. Controller Performance Analysis for A Delayed Process Based on Integral Error Performance Indices. Orient J Chem 2016;32(3). Available from: http://www.orientjchem.org/?p=17896

Introduction

In process industries controlling the process is main issue. For the industries it is very important to keep process working properly for optimum results and good quality of product. Most of the industrial processes have inherent dead time and its existence is extremely undesirable in the processes including chemical processes1-4. Dead time also known as delay time and occurs due to delay involved in measurement devices, final control element and human controller and between two consecutive actions of the process5, 6. The present analysis emphasize on first order plus dead time (FOPDT) process model as they represent a wide class of chemical processes available in chemical industries. The FOPDT process model can be given by the transfer function:

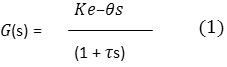
 equation

Where K is process gain, θ is dead time and τ is time constant

A heat exchanger process which can be modelled as FOPDT process model is selected for investigation. A chemical process for heating contains a chemical reactor and a heat exchanger system7. In literature two assumptions are made regarding this process. First assumption is that a liquid level remains constant. The second assumption is heat storage capacity of insulating wall is negligible8.

Proportional Integral controllers are widely used in process industries because of ease and simplicity in tuning9. PI controller used to eliminate steady state error. It is generally used where speed of response is not an issue10. The proportional action gives change in input proportional to the error. The integral action gives integral of error and main purpose is to eliminate offset. The proportional controller then takes the appropriate action11, 12. In general PI controller can be given as

 equation

Performance indices are the quantitative measurement of the system and articulates about the systems optimality. In other words it make a distinction between optimum and non-optimum systems. Systems parameters are so adjusted that index should reach an extreme value probably the minimum value for best performance of the system13. Steady state and dynamic time response characteristics also signifies the performance of the controller and hence the overall performance of the system.

Methodology

In present analysis a heat exchanger which can be modelled as FOPDT process model is selected. After selecting pertinent FOPDT process model, controller parameters are calculated to design PI controller using various tuning techniques such as Ziegler- Nichols, Liptak, Moros, Shinskey and Skogestad. The PI controller is then implemented in the system to control the process, in a closed loop with unity feedback. Integral Error based performance indices viz. ISE, ITAE and IAE performance indices are calculated along with steady state and dynamic time response characteristics using step input. The performance indices and time response characteristics have been compared to gauge the controller performance. Figure 1 gives the flowchart for organized analysis.

Fig. 1: Flowchart for organized analysis 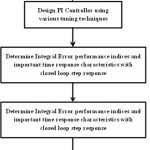Figure 1: Flowchart for organized analysis

Click here to View Figure

The selected FOPDT process model for heat exchanger can be given as:

 Where, process gain = 1

Dead time (θ) = 14.7 sec

Time constant= 21.3 sec

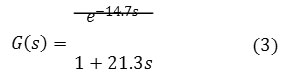
equation
Results and Discussion

Various PI controllers using a number of tuning techniques are designed for the selected FOPDT process model. The closed loop step responses and integral error performance indices are calculated for the system. Figure 2 shows the comparison of closed loop step responses of the process for the PI controller designed using Ziegler- Nichols, Liptak, Shinskey, skogestad, Moros tuning technique.

Table 1: Comparison of important time response characteristics

Tuning techniques Rise Time Settling time
Ziegler-Nicholas

143

298

Liptak

16.6

257
Shinskey

137

309
Skogestad

109

259

Moros

18.9

297

 

Table 2: Comparison of integral error performance indices

Tuning techniques ISE

IAE

 ITAE
Ziegler-Nicholas 34.12

64.97

 4341
Liptak 22.92

42.41

 2536
Shinskey 28.17

56.73

 3885
Skogestad 25.77

49

 2910
Moros 24.18

48.05

 3238

 

Table 1 exhibits the comparison of time response characteristics. The comparison of integral error performance indices viz. IAE, ITAE and ISE are given in Table 2.The minimum rise time and settling time are for the PI controller using Liptak tuning technique, whereas maximum rise time and settling time is obtained using Ziegler Nichols and Shinskey tuning methods respectively. Performance indices are maximum for PI controllers designed using Ziegler Nichols tuning technique and minimum in case of PI controller designed with Liptak tuning technique.

Conclusion

PI controllers have been designed with various tuning techniques, for Heat exchanger process which is modelled as FOPDT process model, to choose one of the best PI controller. For the selected complex industrial process, the PI controller using Liptak tuning technique gives the best time response characteristics and optimum value of performance indices. Hence the PI controller designed using Liptak tuning technique exhibits the best performance in comparison with all the other PI controllers in the heat exchanger process.

References

  1. Normey-Rico, J. E.; Camacho, E. F.; Control Engineering Practice, 2008, 16, 407–428.
    CrossRef
  2. García, P; Albertos, P; Journal of Process Control, 2010, 20, 877–884
    CrossRef
  3. Jangwan, R.; Chaturvedi, M.; Juneja, P.K.; Sunori, S; Singh, P; Proceedings of the International Conference on Advances in Computing, Communications and Informatics, IEEE Xplore, 2014, 712 – 717.
  4. Chaturvedi, M; Juneja, P; IEEExplore, ICAES 2013, 2013, 313-315.
  5. Chaturvedi, M.; Juneja, P.K.; Chauhaan, P; Proceedings of the International Conference on Advances in Computing, Communications and Informatics, IEEE Xplore, 2014, 853 – 858.
  6. Seborg, D. E.; Edgar, T. F.; Mellichamp, D. A.; Wiley, New York, 2004.
  7. Wang X, Ye H. In International Conference on Transportation, Mechanical, and Electrical Engineering, IEEE, 2011, 1036-1039
  8. Kumar, A.; Garg, K. K.; International Journal for Scientific Research & Development,2015, 3 (04).
  9. Padhy, P. K.; Majhi, S; Computers & Chemical Engineering, 2006, 30 (5), 790-796.
    CrossRef
  10. Chidambaram, M.; Hung. J. Ind. Chem., 1994, 22, 37-43.
  11. O’Dwyer, A.; Imperial College Press, London, 2003, 57.
  12. Shamsuzzoha, M; Lee, M.; Industrial & Engineering Chemistry Research, 200746(7), 2077-91.
    CrossRef
  13. Balestrino, A.; Landi, A; Medaglia, M.; Satler, M.; In 14th Mediterranean Conference on Control and Automation, IEEE, 2006, 16.

Creative Commons License
This work is licensed under a Creative Commons Attribution 4.0 International License.