Borane Clusters Hiding Inside Carbonyl Clusters
Enos Masheija Kiremire
Department of Chemistry and Biochemistry University of Namibia, Private Bag 13301, Windhoek Namibia. Corresponding Author Email: kiremire15@yahoo.com
DOI : http://dx.doi.org/10.13005/ojc/31.Special-Issue1.15
This paper is based upon the 14n Rule for transition metal carbonyl clusters and the for 4n rule for borane clusters. It reveals that the when the shielding 10n electrons are removed from the 14n based cluster what remains is a cluster that obeys the 4n rule. For instance it shows that Os5(CO)16 (14n+2) cluster of 72 valence electrons corresponds to B5H52- (4n+2) of 22 electron cluster, and Rh6(CO)16 (14n+2) corresponds to B6H62- cluster(4n+2) of 26 electrons. It is also shows that some of the giant clusters are equivalent to simple borane clusters when the shielding electrons are removed. The borane clusters so derived can readily be categorized into series which correspond to those of the carbonyl clusters. The isolobal concept has also been found to conform to cluster series.
KEYWORDS:Borane Clusters; transition metal
Download this article as:| Copy the following to cite this article: Kiremire E. M. Borane Clusters Hiding Inside Carbonyl Clusters. Orient J Chem 2015;31(Special Issue1). |
| Copy the following to cite this URL: Kiremire E. M. Borane Clusters Hiding Inside Carbonyl Clusters. Orient J Chem 2015;31(Special Issue1). Available from: http://www.orientjchem.org/?p=10728 |
Introduction
The existence of series in boranes and carbonyl clusters were discovered by Wade and Mingos1-2. Their studies were supported by Molecular Orbital Theory. Recently, it has been found that the carbonyl and borane clusters in fact do encompass a wide spectrum of series3-4. These series which are interrelated and are based on 14n and 4n rules3-4. If the carbonyl series are given by ST = 14n+q and the corresponding main group elements are given by SG= 4n+q where q can take up multiple integers of 2, positive or negative, then it became clear that ST = (14n+q)-10n = SG = 4n+q. This implies that if we remove 10n value electrons from the valence electrons (V) of a carbonyl cluster we will have the remaining electrons (VT) available for conversion into a corresponding formula of a compound of the main group element. With this in mind, the correlation was focused mainly on converting carbonyl clusters into borane clusters. These findings are presented in Table 1.
Results and Discussion
The removal of 10n electrons from carbonyl clusters clearly revealed the close relationship between the 14n series for the transition metal carbonyl clusters and the 4n series of main group elements especially the boranes. The method involves first calculating the valence electrons(V) of the carbonyl cluster. Then subtracting the equivalent 10n electrons. The remaining electrons (VT) are distributed between equivalent valence electrons of boron skeletal atoms (VB) and the valence electrons of the hydrogen atoms (VB) assumed to be associated with boron skeletal atoms. For example, Os5(CO)16, V = 8X5+16X2 = 72, VT = 72-50 = 22, VB = 5X3 = 15, VH = VT-VB = 22-15 = 7. Hence, the borane cluster formula (FB) corresponding to Os5(CO)16 cluster = B5H7 = B5H52-. Other borane clusters have been derived in the same way. More examples are illustrated in Schemes 1 and 2.
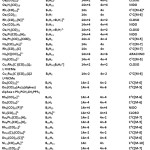 |
Table 1: Equivalence Relationship of Carbonyl and Borane Clusters Click here to View table |
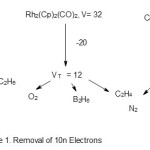 |
Scheme 1 Click here to View scheme |
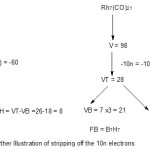 |
Scheme 2 Click here to View scheme |
Equivalence Relationship In Series
hen the carbonyl series of transition metals and that of the main group elements are scrutinized, then the equivalence relationship between them is clearly discerned. That is if the carbonyl series of the transition metal are given by ST = 14n + α and that of the main group elements by SG = 4n+ β such that α = β including the sign before it, then equivalence relationship between the series does exist. For instance, 14n Ξ 4n (Monocapped series) as α = β = 0. Similarly 14n +2 Ξ 4n +2( Closo series), 14n+4 Ξ 4n+4(Nido series), 14n+6 Ξ 4n+6 (Arachno), 14n+8 Ξ 4n+8 (Hypho),14n +10 Ξ 4n+10(Klapo), 14n-2 Ξ 4n-2 (Bicapped),14n-4 Ξ4n-4(Tricapped), 14n-6 Ξ 4n-6(Tetracappe),14n-8 Ξ4n-8(Pentacapped), 14n-10 Ξ4n-10(Hexacapped) and so on. Therefore, the removal of 10n electrons from a transition metal carbonyl series converts it into an equivalent series of the main group element. This is the principle underlying the clusters presented in Table 1. Many examples other than those presented in the table can be derived.
Structural Relationship of the Cluster Series
Closo, Nido and Arachno
It is important to briefly explain the terms closo, nido and arachno before touching on equivalence relationship between boranes and carbonyl clusters. These are terms that evolved with the discovery of boranes. They are actually series of compounds which were found to possess structural relationship that was observed within them and reported by Rudolph2a. The closo ones have the ideal geometries with all the atoms linked with triangular sides. An example is the octahedral B6H62−with six skeletal atoms[M-6]. When one atom is removed an ideal square pyramid shape is produced such as B5H9 (M-5). The result shape is that of a nido cluster regarded as derived from the octahedral closo system [M-6]. The removal of another atom from B5H9 (M-5) gives a 4-skeletal atom cluster B4H10(M-4). This is regarded as arachno with two atoms missing from the shape of the original closo octahedral geometry. As we have observed, the spectrum of series especially the carbonyls is wide.
Consider Os5(CO)16 and B5H52- clusters. For the carbonyl cluster, n = 5, 14n = 14×5 = 70 and number of valence electrons(V) =5×8+16×2 = 72 and hence its series (ST = 14n +2 = 72). Also its corresponding cluster number k = 2n-1 = 2×5-1 = 9. This means the carbonyl cluster belongs to 14n+2 series. In the case of the borane cluster, n =5 as well, 4n =4×5 =20 and V =5×3+5+2 = 22 and so SG = 4n+2 = V and likewise it belongs to 4n +2
series. Its k value = 2n-1 = 2×5-1 =9. This implies that Os5(CO)16 and B5H52― clusters are equivalent and their cluster number k values are equal. Hence, it is likely that their skeletal atom geometries will be similar. Indeed, the skeletal atoms of the two clusters portray a trigonal bipyramid5 shape as sketched in Figure 1.
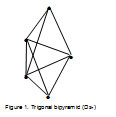 |
Figure 1 Click here to View figure |
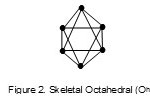 |
Figure 2 Click here to View figure |
The clusters Rh6(CO)16 (V = 86) and B6H62-(26) are equivalent5 since the former belongs to 14n+2 while the later 4n+2. Furthermore, their cluster number values k = 11 are equal and they also have an octahedral skeletal geometry as sketched in Figure 2. Just to familiarize ourselves with the method of establishing the equivalence relationship, let us work on this example. This is well illustrated in Scheme 3.
 |
Scheme 3 Click here to View scheme |
In exploring the equivalence relationship further, let us focus on diatomic skeletal systems further. The cluster system Rh2(Cp)2(CO)26 is equivalent to B2H6, C2H4, and O2. The rhodium cluster belongs to the nido series 14n+4 and with k- value of k = 2n-2 = 2. This means that the two atoms are linked with a double bond, Rh=Rh. Similarly, in the diatomic atoms O2, and C2 in C2H4 will be doubly linked, O=O, and C=C.
However in the case of B2H6 the double bond is represented by two banana bonds5 as sketched in Figure 3.
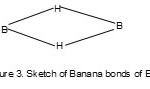 |
Figure 3 Click here to View figure |
The carbonyl complex6, Cr2(Cp)2(CO)4 belongs to closo series (14n+2) with k = 2n-1 = 2×2-1 =3. This means that the two chromium atoms are triply linked, that is, CrΞCr. As can be seen from Table 1,this complex is equivalent to C2H2(4n+2), with k=2n-1 =3. The C2H2 diatomic skeletal molecule indeed has a triple bond, CΞC. The Mn2(CO)10 belongs to the Arachno series(14n+6) with k =2n-3 =2×2-3=1. Therefore the manganese carbonyl has a
single bond Mn-Mn. It is equivalent to C2H6 (C-C) and F2(F-F) which belong to 4n+6 series and do have single bonds. What is fascinating is what the shape of B2H8(4n+6) will be. What is also interesting is that theoretical studies7 which have been done on BH5(4n+4) and B2H8(4n+6) molecules which unlike their hydrocarbon counterparts CH4 (4n+4) and C2H6 (4n+6) are unstable. On the basis of the work done by Olah, etal7, the possible structures of the hypothetical molecules BH5 and B2H8 are sketched in Figure 4. Also according to the series, the B2H8(4n+6) molecule is expected to have a single bond k = 2n-3 = 2×2-3 = 1. As can be deduced from the series, the counterparts for BH5 are CH4 and its analogues such as SiH4, GeH4, SnH4 and PbH4 belong to 4n+4 series as well as carbonyls such as Fe(CO)5, Ru(CO)5, and Os(CO)5 which belong to 14n+4 series. The bond between the H2 and B atom is a simplified form of a three-centered bond.
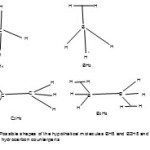 |
Figure 4 Click here to View figure |
Capping Series
The capping carbonyl series give rise to corresponding capped boranes. Many of the hypothetical capped borane series equivalents are useful in categorization of carbonyl clusters. For instance Os10(C )(CO)242- is equivalent to B10H4. The series for B10H4 can be determined as n = 10, 4n = 40 and V = 10×3+4 = 34 and hence SG = 4n-6 =34 = V. This series can be written as 4n +3(-2). We know from the knowledge of series that 4n represents the first capping C1 and that every (-2) multiple after the 4n represents an additional capping, this means that the series 4n-6, has Cp = C1 +C3 = C4C. By extrapolating B10H4 to Os10(C )(CO)242- complex, then it can be deduced that the carbonyl cluster is tetra-capped octahedral C4C[M-6] as it known to be the case8. This code is also important as it indicates that the cluster is in the row number six[M-6] beginning from M-1 of the column in which the closo [M-6] is found and then the cluster capped based on [M-6] is in column number six from the closo system [M-6] in the capping series3-4.
| Table 2. Valence Correlation Between Carbonyl cluster and Main Group Cluster | ||||||
| Generating | ||||||
| Function | Carbonyl | Main Group | ||||
| Closo Series | Formula | V= S= 14n+2 | 4n+2 | |||
| F(n) | → | 3n+1 | ||||
|
1 |
4 |
Os(CO)4 |
16 |
6 |
||
|
2 |
7 |
Os2(CO)7 |
30 |
10 |
||
|
3 |
10 |
Os3(CO)10 |
44 |
14 |
||
|
4 |
13 |
Os4(CO)13 |
58 |
18 |
||
|
5 |
16 |
Os5(CO)16 |
72 |
22 |
||
|
6 |
19 |
Os6(CO)19 |
86 |
26 |
||
|
7 |
22 |
Os7(CO)22 |
100 |
30 |
||
|
8 |
25 |
Os8(CO)25 |
114 |
34 |
||
|
9 |
28 |
Os9(CO)28 |
128 |
38 |
||
|
10 |
31 |
Os10(CO)31 |
142 |
42 |
||
The derivation of main group compound equivalent to a carbonyl cluster could easily be reflected in Table 2 of closo series. For instance in case of Os(CO)4 (V =16) if 10 (n =1)valence electrons are removed then 6 valence electrons will remain. This corresponds to the elements of group 6(or 16) such O, S, Se, and Te, or a combination of fragments such as CH2 or CR2. This clearly is in full agreement with Hoffman’s isolobal concept9. In the case of Os2(CO)7, the valence electrons of 10 for n = 2, could correspond to species such as N2 and C2H2.
Conclusion
The results obtained and displayed in Tables 1and 2 strongly support of power of the 14n and 4n series and their applications to categorize carbonyl and main group element clusters. They are also in agreement with the Hoffmann’s isolobal concept. The assumption is that the skeletal elements in transition metal carbonyl clusters must obey the 18 electron rule while those in the main group elements must obey the octet rule. This work greatly complements what has been published elsewhere in literature on carbonyl and borane clusters1-2,10-13.
Acknowledgement
The author wishes to acknowledge the University of Namibia for financial and material support, NAMSOV, Namibia for generous funding and my wife, Merab Kambamu Kiremire for her encouragement to write up this paper.
References
- Wade, K. ,J. Chem. Soc., Dalton, 1971, 792-793.
- (a) Mingos, D. M. P., Nature Physical Science, 1972, 236, 99-102. (b) Welch, A. J. Chem. Soc., Chem. Comm., 2013,49, 3615-3616.
- Kiremire, E.M., Orient. J. Chem., 2014, 30(4), 1475-1485.
- Kiremire, E.M., Orient. J. Chem., 2015, 31(1), 387-392.
- Cotton, F. A., Wilkinson, G., ‘Advanced Inorganic Chemistry’, 4th Edition, John Wiley & Sons, New York, 1980.
- Crabtree, R. H., ‘The Organometallic Chemistry of The Transition metals’, 4th Edition, John Wiley and Sons, Inc., New Jersey, 2005.
- Olah, G. A., Prakash, G. K., S., Rasul, L., PNAS, 2012, 109(18), 6825-6828.
- Teo, B. K., Longoni,G., Chung, F. R. K., Inorg. Chem., 1984, 23, 1257-1266.
- Hoffmann, R., Angew. Chem. Int. Edition, 1981, 21(10), 711-724.
- Hughes, A. K., Wade, K., Coord. Chem. Rev., 2000, 197, 191-229.
- Rudolph, R. W.,Accounts Chem. Res., 1976, 9(12), 446-452.
- Belyakova, O. A., Slovokhotov, Y. L., Russian Chemical Bulletin, International Edition, 2003, 52(11), 1-29.
- King, R. B., Inorg. Chimica Acta, 1986, 116, 99-107.

This work is licensed under a Creative Commons Attribution 4.0 International License.









