SWNTs and MWNTs (M=2) for Nano Drug Delivery: Temperature and Solvent effect

Introduction

The highly electrophilic central carbon atom of the -N=C=S group reacts rapidly, and under mild conditions with oxygen-, sulfur-, or nitrogen centered nucleophiles to give rise to carbamates, thiocarbamates, or thiourea derivatives, respectively. The -NCS group of isothiocyanates absorbs UV light with low intensity near 240 nm. Among the most extensively investigated isothiocyanates is PEITC which occurs naturally as glucosinolate in a variety of cruciferous vegetables such as: kale, turnip, cabbage and broccoli. Phenethyl-ITC (PEITC) is one of the best-studied members of the ITC family of compounds that has generated a great deal of research interest due to its cancer chemopreventive activity [1-10]. Angiogenesis (formation of new blood vessels): cancer, rheumatoid arthritis, endometriosis and diabetic retinopathy. Therefore, antiangiogenic therapy represents one of the most promising approaches to control tumor growth and invasiveness. PEITC inhibits transcriptional activity of nuclear factor-kB (NF-kB) and suppresses expression of NF-kB–regulated genes, including vascular endothelial growth factor (VEGF) 3, 4], Because VEGF plays an important role in angiogenesis by promoting endothelial cell proliferation, migration, and differentiation. PEITC effectively inhibits in vitro angiogenic features. PEITC effectively inhibited chemically-induced lung, mammary gland, forestomach and esophagus tumorigenesis. Phenethylisothiocyanate exhibits antileukemic activity in vitro and in vivo [2-10].

The carbon nanotube (CNT) is a representative nano-material. CNT is a cylindrically shaped carbon material with a nanometric-level diameter [11-18].

Its structure, which is in the form of a hexagonal mesh, resembles a graphite sheet and it carries a carbon atom located on the vertex of each mesh. The sheet has rolled and its two edges have connected seamlessly [19-25].

Although it is a commonplace material using in pencil leads, its unique structure causes it to present characteristics that had not found with any other materials. CNT can be classified into single-wall CNT, double-wall CNT and multi-wall CNT according to the number of layers of the rolled graphite [26,30].

The type attracting most attention is the single-wall CNT, which has a diameter deserving the name of “nanotube” of 0.4 to 2 nanometers. The length is usually in the order of microns, but single-wall CNT with a length in the order of centimeters has recently released [31,40].

CNT can be classified into single-wall CNT, double-wall CNT and multi-wall CNT according to the number of layers of the rolled graphite. The type attracting most attention is the single-wall CNT, which has a diameter deserving the name of “nanotube” of 0.4 to 2 nanometers [28-32].

The length is usually in the order of microns, but single-wall CNT with a length about centimeters have recently released. The extremities of the CNT have usually closed with lids of the graphite sheet [40-49].

The lids consist of hexagonal crystalline structures (six-membered ring structures) and a total of six pentagonal structures (five-membered ring structures) placed here and there in the hexagonal structure [50-55]. The first report by Iijima was on the multiwall form, coaxial carbon cylinders with a few tens of nanometers in outer diameter [49-56]. Two years later single walled nanotubes were reported [57-63]. SWCNTs have considered as the leading candidate for nano device applications because of their one-dimensional electronic bond structure, molecular size, and biocompatibility, controllable property of conducting electrical current and reversible response to biological reagents hence SWCNTs make possible bonding to polymers and biological systems such as DNA and carbohydrates[64-69].

So, The structure ofSWCNT as well as their dipole moments and relative energies have been studied by molecular dynamics simulation and quantum mechanics calculations within the Onsager self – consistent reaction field (SCRF) model using a Hartree-Fockmethod (HF) at the HF/3-21G level and the structural stability of considered nanotube in different solvent media and temperature have been compared and analyzed.We investigate effects of water, methanol and a mixture of them on interaction of Temozolomide with SWCNT, utilizing these force fields too [48-66].

The calculations have been done with the GAUSSIAN 98 program according to Hartree-Fock (HF) theory at the HF/STO-3G level. Gibbs free energy,enthalpy,entropy and dipole moment values are compared in gas phase, water and methanol, in this research[64-80]. Thus, by utilizing a Hartree-Fock method, we studied the effects of different  solvents on interaction of Temozolomide with  open-end of  SWCNT within the onsager  self-consistent reaction field (SCRF) model,  and the temperature effects on the stability of the interaction between Temozolomide and single-walled carbon in various solvents[80-97].

Computional Details

The term “Ab Initio” is given to computations which are derived directly from theoretical principles, with no inclusion of experimental data. The most common type of ab initio calculation is called a HartreeFock calculation (abbreviated HF), in which the primary approximation is called the central field approximation. A method, which avoids making the HF mistakes in the first place, is called Quantum Monte Carlo (QMC). There are several flavors of QMC variational, diffusion and Green’s functions. These methods work with an explicitly correlated wave function and evaluate integrals numerically using a Monte Carlo integration. These calculations can be very time consuming, but they are probably the most accurate methods known today. In general, ab initio calculations give very good qualitative results and can give increasingly accurate quantitative results as the molecules in question become smaller.

There are three steps in carrying out any quantum mechanical calculation in HyperChem 7.0 program package [68]. First, prepare a molecule with an appropriate starting geometry. Second, choose a calculation method and its associated options. Third, choose the type of calculation with the relevant options.DFT is based on a theorem due to Hohenberg and Kohn, which states that all ground state properties are functions of the total electronic charge density ρ(r).There are several different DFT functional available differing primarily in the choice of the basis functions, in which, the electronic wave functions are expanded and the scheme of integration.[69,70].

The Becke’s three parameter exact exchange functional (B3) combined with gradient corrected correlation functional of Lee–Yang–Parr (LYP) have been employed to calculate energy, dipole moment, charge distribution and thermo chemical data and  NMR  parameters by implementing the 6-31G,STO-3G basis sets.  All the NMR shielding parameters were calculated supposing gauge-included atomic orbital (GIAO) method.

NMR spectroscopy is a research technique that exploits the magnetic properties of certain atomic nuclei to determine physical and chemical properties of atoms or the molecules in which they are contained. It relies on the phenomenon of nuclear magnetic resonance and can provide detailed information about the structure, dynamics, reaction state, and chemical environment of molecules. Ab initio calculation of nuclear magnetic shielding has become an indispensable aid in the analysis of molecular structure and accurate assignment of NMR spectra of compounds.

NMR is based on the quantum mechanical property of nuclei. The chemical shielding refers to the phenomenon, which is associated with the secondary magnetic field created by the induced motions of the electrons that surrounding the nuclei when in the presence of an applied magnetic field. In general, the electron distribution around a nucleus in a molecule is more spherically symmetric. Therefore, the size of electron current around the field, and hence the size of the shielding, will depend on the orientation of the molecule within the applied field B₀.

Calculations of nucleus-dependent and -independent chemical shifts were carried out using the gauge-invariant atomic orbital (GIAO) approach.

Calculations were performed using an all-electron linear combination of atomic orbitals Hatree–Fock (HF) and density functional theory (DFT) calculations using the Gaussian 03 package. The optimizations of (2-fluoro-2-isothiocyanatoethyl)benzene, (2-chloro-2 isothiocyanatoethyl)benzene, (2-bromo-2-isothiocyanatoethyl)benzene, (2 isothiocyanatopropyl)benzene, (2-isothiocyanato Butyl)benzene and (1-isothiocyanatoethane-1,2-diyl) di benzene (used in this study are shown in Figure. 2)  are carried out including exchange and correlation contributions using Beckẻs three parameter hybrid and Lee-Yang-Parr (LYP) correlation [B3LYP]; including both local and non-local terms. We have geometric optimization calculation at the HF/6-31G, HF/6-31G**, HF/6-311G**. We have also performed a geometric optimization calculation at the B3LYP/6-31G, B3LYP/6-31G** and B3LYP/6-31G** level. The NMR isotropic shielding constants were calculated using the standard GIAO (Gauge-Independent Atomic Orbital) approach of Gaussian 03 program package [98].

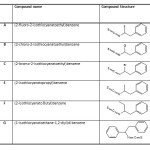Table 1: Chemical shifts of the considered compounds were calculated at the same level using the Gauge- Included Atomic Orbital (GIAO) approach.  Click here to View table

 

Molecular mechanics (Monte Carlo simulation)

The Metropolis implementation of the Monte Carlo algorithm has been developed by studying the equilibrium thermodynamics of many-body systems. Choosing small trial moves, the trajectories obtained applying this algorithm agree with those obtained by Langevin’s dynamics. This is understandable because the Monte Carlo simulations always detect the so-called “important phase space” regions which are of low energy. Because of imperfections of the force field, this lowest energy basin usually does not correspond to the native state in most cases, so the rank of native structure in those decoys produced by the force field itself is poor.

In density function theory the exact exchange (HF) for a single determination is replaced by a more general expression the exchange correlation functional, which can include terms accounting for both exchange energy and the electron correlation, which is omitted from Hartree-Fock theory:

 

where E_χ(p) is the exchange function and E_C(p) is the correlation functional.

Langevin dynamics (LD) simulation

The Langevin equation is a stochastic differential equation in which two force terms have been added to Newton’s second law to approximate the effects of neglected degrees of freedom .These simulations can be much faster than molecular dynamics.The molecular dynamics method is useful for calculating the time dependent properties of an isolated molecule. However, more often, one is interested in the properties of a molecule that is interacting with other molecules.

Results and Discussion

We used different force field to determination of energy and other type of geometrical parameters, on the particular SWCNT, and DWCNTs Because of the differences among force fields, the energy of a molecule calculated using two different force fields will not be the same.In the process of investigating the combination of particular molecules and CNT to achieve more information about these important gene transfer systems, we attempted to construct different (2-fluoro-2- isothiocyanatoethyl) benzene, (2-chloro-2- isothiocyanatoethyl) benzene, (2-iso-thiocyanatopropyl) benzene, (2-bromo-2-isothiocyanatoethyl)benzene and (2-isothiocyanatoButyl)benzene and link them individually to outer surface of SWCNT to develop practical application of these molecules to interact with SWNTs and DWCNTs. These coupling have been performed between C atom of nanotubes and halogen of molecules.In Fig.1 the couplings between these molecules and single wall nano tubes with outer surface of SWNT has been displayed. Optimizations of these structures have been performed by using UFF and AM1[71].

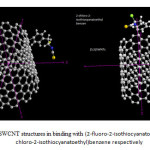Figure 1: (5,5) and (9,9) SWCNT structures in binding with (2-fluoro-2-isothiocyanatoethyl)benzene and (2-chloro-2-isothiocyanatoethyl)benzene respectively  Click here to View figure

 

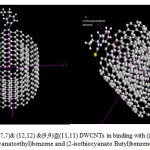Figure 2: (7,7)& (12,12) &(9,9)@(11,11) DWCNTs in binding with ((2-bromo-2-isothiocyanatoethyl)benzene and (2-isothiocyanato Butyl)benzene respectively  Click here to View figure

 

So, it is not reasonable to compare the energy of one molecule calculated with a particular force field with the energy of another molecule calculated using a different force field. In this study difference in force field illustrated by comparing the energy of calculated by using force fields, MM+, Amber and OPLS. Theoretical energy values using different force fields, which is the combination of attraction van der Waals forces due to dipole-dipole interactions and empirical repulsive forces due to Pauli repulsion has been demonstrated in Table1.Since the solute dipole moment induces a dipole moment in opposite direction in the surrounding medium.

Table 1: Calculated dipole moment and optimized energy parameters(relative) with different levels of Theory, which are affected by different dielectric constants. 

Media		Temperature Dipole moment Energy
a		305 5.54 -51.1211	307 4.44 -51.0136	309 3.89 -51.083	311 7.9 -55.373	313 4.5 -63.534	315 3.22 -47.443	317 4.33 -56.610	319 4.25 -33.968	321 3.45 0.0
b		1.02 -34.927	2.714 -35.496	2.25 -37.185	1.34 -49.365	1.276 -38.160	3.95 -30.994	1.916 0.0	1.653 -30.44	2.997 -35.442
c		6.4 -36.34	5.03 -25.247	3.83 -35.165	3.55 -33.345	5.84 -34.55	4.33 0.0	2.44 -34.555	5.31 -17.361	6.66 -26.231
e		1.152 -39.48	4.194 -42.35	3.261 -47.36	3.416 -55.33	2.44 0.0	3.565 -36.26	3.461 -37.26	2.44 -34.55	2.651 -38.98
f		2.84 -31.72	1.68 -34.31	3.55 0.0	2.58 -23.82	1.27 -33.259	3.28 -43.156	2.77 -46.18	1.94 -40.46	2.961 -62.287
g		3.218 -51.27	2.726 -38.561	3.943 -56.234	3.149 -54.48	3.242 -42.57	5.645 -35.545	3.345 -35.72	3.83 -43.635	4.46 0.0
		HF		B3LYP		Molecular Mechanic Methods		E
(7,7)SWNTS		E×10-5 Sto-3g 3-21g	μ Sto-3g 3-21g	E Sto-3g 3-21g	μ Sto-3g 3-21g		Dielectric constant	MM+	Amber	OPLS
(11,11)SWNTS		-35.24	29.85	-42.36	43.85		1	472.55	250.32	317.77
		-35.49	75.59	-72.65	68.61		78.00	422.56	862.79	375.63
(7,7)@(12,12)DWNTS		-52.55	31.51	-56.29	36.79		32.00	540.69	176.17	364.42
		-42.36	47.55	-50.63	23.30		24.00	224.12	147.42	516.47
(5,5)@(10,10)DWNTs		-34.57	34.69	-62.65	16.81		70.00	541.65	360.79	247.74
		-22.76	64.14	-34.03	23.34		72.00	545.18	149.87	391.12

 

Figure 2: The chart of optimized energy using theoretical methods in various media, for SWNTs and DWNTS  Click here to View figure

 

Also, polarization of the medium in turn polarizes the charge distribution in the solvent. The dipole moment value of SWCNT in different solvent media at same temperatures has been reported.

References

1. Brzezinski, W.Medelewski, P. Z Pflanzenzuchtg.1984, 93, 177-183.
2. Fahey, J. Zalcmann,A.T.Talalay, P. Phytochemistry.2001, 56, 5–51
3. Nugon-Baudon, L.Rabot, S.Flinois, J-P.Lory, S.Beaune, P. Br. J. Nutr.1998,80, 231–234,
4. Grubbs, C. J.Steele, V. E.Casebolt, T.Juliana, M.M.Eto, I.Whitaker,L.M.Dragnev,K. H.Kelloff, G. J.Lubet, R. L. Anticancer Res.1995,15,709– 716
5. Nakagawa, H.Tsuta, K.Kiuchi, K.Senzaki, H.Tanaka, K.Hioki, K.Tsubura, A. Carcinogenesis (Lond.),2001,22,891–897
6. Wattenberg, L. W. Cancer Res.1981,41, 2991–2994
7. Bresnick, E.Birt, D. F.Wolterman, K.Wheeler, M.Markin, R. S. Carcinogenesis (Lond.),1990, 11,1159–1163
8. Stoewsand, G. S. Anderson, J. L. and Munson, L. Cancer Lett.1988, 39,199–207
9. Bogaards, J. J.Verhagen, H. Willems, M. van Poppel, G.van Bladeren, P. J Carcinogenesis (Lond.),1994, 15, 1073–1075
10. M. Monajjemi & J. Najafpour , Fullerenes, Nanotubes, and Carbon Nanostructures, 2014,22(6),575–594,.
11. Monajjemi, M.Baei, M.T.Mollaamin, F. Russian Journal of Inorganic Chemistry. 2008, 53 (9), 1430-1437
12. Monajjemi, M. Rajaeian, E. Mollaamin, F.Naderi, F.Saki, S. Physics and Chemistry of Liquids. 2008, 46 (3), 299-306
13. Monajjemi, M. Seyed Hosseini, M. Journal of Computational and Theoretical Nanoscience 2013 ,10 (10), 2473-2477
14. Yahyaei ,H.Monajjemi, M. Fullerenes, Nanotubes, and Carbon Nanostructures.2014, 22(4), 346–361
15. Monajjemi, M .Jafari Azan, M.Mollaamin, F. Fullerenes, Nanotubes, and Carbon Nanostructures.2013, 21(6), 503–515
16. Bhupesh Bishnoi.Bahniman Ghosh ,Quantum Matter,2014, 3, 469-475
17. SuleCelasun ,Rev. Theor. Sci. 2013,1, 319-343
18. Nafisi, S.Monajemi, M.Ebrahimi, S.  Journal of Molecular Structure.2004,705 (1-3) 35-39
19. Monajjemi , M.Baheri ,H.Mollaamin ,F.  Journal of Structural Chemistry.2011, 52(1), 54-59
20. Monajjemi, M.Seyed Hosseini, M. Mollaamin, F. Fullerenes, Nanotubes, and Carbon Nanostructures. 2013, 21, 381–393
21. DavideFiscaletti.AmritSorli ,Quantum Matter,2014, 3, 200-214
22. Monajjemi, M.  Boggs, J.E.  J. Phys. Chem. A, 2013,117,1670 −1684
23. Monajjemi , M. Honaparvar , B. KhaliliHadad ,B. Ilkhani ,AR. Mollaamin, F. Afr. J. Pharm. Pharmacol .2010, 4 (8), 521-529
24. Piglosiewicz,B.;Vogelsang,J.Schmidt,S.JaePark,D.Groß,P.Lienau, C ,Quantum Matter.2014, 3, 297-306
25. Monajjemi, M. Chemical Physics. 2013, 425, 29-45
26. Fazaeli ,R.Monajjemi ,M.Ataherian ,F.Zare, K. Journal of Molecular Structure THEOCHEM.2002, 581 (1), 51-58
27. Monajjemi, M.Mollaamin, F, J Clust Sci,2011,22,673.
28. Anurag Srivastava, NileshiSaraf, and A. K. Nagawat , Quantum Matter.2013, 2, 401-407
29. IijimaSumio. Nature (London), 1991,354, 56.
30. S. Iijima, Nature, 1991,354, 56.
31. S,Iijima,S.Ichihasi,T,Nature,1993,363, 603
32. Bethune,D. S.Kiang,C. H.deVries,M. S. Gorman,G.;Vazques, J. Beyers,R,Nature ,1993,363, 605
33. Ramanathan,T.Fisher,F.T.Ruoff,R.S.Brinson,L.C.Chem mater,2005  17, 1290
34. Monajjemi, M .Sobhanmanesh, A .Mollaamin, F.Fullerenes, Nanotubes, and Carbon Nanostructures,2013, 21,47–63
35. Monajjemi ,M.Karachi ,N.Mollaamin, F. Fullerenes, Nanotubes, and Carbon Nanostructures, 2014, 22,643–662
36. Davide Fiscaletti,Rev. Theor. Sci.2013,1, 103-144
37. Monajjemi, M. Mahdavian, L.  Mollaamin, F. Bull .Chem.Soc.Ethiop ,2008, 22(2),1-10.
38. Guo,J.-Y.. Xu,C.-X. . Sheng,F.-Y. .Jin, Z.-L.Shi,Z.-L. Dai,J. . Li,Z.-H. Quantum Matter,2013,2, 181-186
39. Mollaamin ,F. Baei, MT. Monajjemi, M.Zhiani , R.;Honarparvar , B. Russian Journal of Physical Chemistry A, Focus on Chemistry,2008, 82, (13), 2354-2361
40. Monajjemi, M.Ghiasi, R. Ketabi, S. Journal of Chemical Research.2004, 1,11-18
41. Mahdavian,L. Monajjemi, M.Mangkorntong ,N.Fullerenes, Nanotubes and Carbon Nanostructures,2009, 17 (5), 484-495
42. Mollaamin, F. Gharibe, S. Monajjemi, M. Int. J. Phy. Sci ,2011,6, 1496-1500
43. Monajjemi, M . Faham, R. Mollaamin, F.Fullerenes, Nanotubes, and Carbon Nanostructures 2012 20, 163–169
44. Monajjemi, M. Khaleghian, M. Tadayonpour, N. Mollaamin, F. International Journal of Nanoscience,2010, 9 (05), 517-529
45. Mollaamin , F .Najafi ,F. Khaleghian, M.  KhaliliHadad, B. Monajjemi ,M. Fullerenes, Nanotubes, and Carbon Nanostructures,2011,19, 653–667
46. Monajjemi, M. Chegini , H.  Mollaamin , F. Farahani ,P,Fullerenes, Nanotubes, and Carbon Nanostructures.2011,19, 469–482
47. Monajjemi, M.Yamola ,H. Mollaamin,F.Fullerenes, Nanotubes, and Carbon Nanostructures 2014, 22, 595–603
48. Monajjemi, M. Heshmata, M. Haeri, HH , Biochemistry (Moscow),2006, 71 (1), S113-S122
49. Monajjemi, M.  TheorChemAcc ,2015, 134:77 DOI 10.1007/s00214-015-1668-9
50. A. Rubio. J.L. Corkill.M.L. Cohen. Phys. Rev. B ,1994, 49, 5081
51. X. Blasé. A. Rubio.S.G. Louie. M.L. Cohen. Europhys.Lett,1994.28, 335.
52. N.G. Chopra. J. Luyken. K. Cherry. V.H. Crespi. M.L. Cohen,S.G. Louie. A. Zettl, Science.1995 , 269, 966
53. N.G. Chopra.A. Zettl.Solid State Commun.1998 ,105, 297
54. J. Cumings. A. Zettl, Solid State Commun.2004, 129, 661
55. R. Ma.Y. Bando. H. Zhu.T. Sato, C. Xu, D. Wu, J. Am.Chem. Soc.2002, 124, 7672,
56. P.W. Fowler, K.M. Rogers, G. Seifert, M. Terrones, and H. Terrones, Chem. Phys. Lett. 1999, 299, 359
57. Monajjemi, M . Falahati, M. Mollaamin, F. Ionics, 2013 , 19, 155–164
58. Monajjemi , M. Heshmat ,M. Aghaei , H. Ahmadi , R. Zare,K. Bulletin of the Chemical Society of Ethiopia, 2007,21 (1)
59. Monajjemi , M.  Lee, V.S.  Khaleghian, M.  B. Honarparvar, B.  F. Mollaamin, F, J. Phys.Chem. C. 2010, 114 (2010) 15315
60. A. Rubio, J.L. Corkill, M.L. Cohen, Phys. Rev. B.1994, 49,5081
61. X. Blase, A. Rubio, S.G. Louie, M.L. Cohen, Europhys. Lett.1994, 28, 335.
62. N.G. Chopra, J. Luyken, K. Cherry, V.H. Crespi, M.L. Cohen,S.G. Louie, A. Zettl, Science ,1995, 269, 966.
63. O.R. Lourie, C.R. Jones, B.M. Bartlett, P.C. Gibbons, R.S. Ruoff,W.E. Buhro, Chem. Mater.2000, 12 ,1808
64. R. Ma, Y. Bando, T.Sato, Chem. Phys. Lett.2001,337 ,61.
65. W. Han, Y. Bando.; K. Kurashima.; T. Sato, Appl. Phys. Lett.1998,73, 3085
66. (a) D. Golberg. Y. Bando.M. Eremets. K. Takemura. K. Kurashima.H.Yusa, Appl. Phys. Lett.1996 ,69, 2045
67. D.P. Yu, X.S. Sun, C.S. Lee, I. Bello, S.T. Lee, H.D. Gu, K.M. Leung, G.W. Zhou, Z.F. Dong. Z. Zhang. Appl. Phys. Lett.1998,72 , 1966.
68. F.Jensen. H.Toftlund, Chem. Phys. Lett.1993, 201,89 , 94
69. Monajjemi, M . Aghaie , H. Naderi , F. Biochemistry (Moscow).2007,72 (6), 652-657
70. Monajjemi, M.  Journal of Molecular Modeling , 2014, 20, 2507
71. Davide Fiscaletti,Rev. Theor. Sci.2013 1, 103-144
72. Monajjemi , M. Chahkandi ,B.  Zare,K. Amiri, A. Biochemistry (Moscow),200,70, (3), 366-376
73. Monajjemi, M . Afsharnezhad ,S. Jaafari , M.R. Abdolahi ,T. Nikosade ,A. Monajemi ,H.Russian Journal of physical chemistry A, 2007,2,1956-1963
74. Monajjemi, M. Khaleghian, M,  Journal of Cluster Science. 2011, 22(4), 673-692
75. Mollaamin , F. Monajjemi , M , Journal of Computational and Theoretical Nanoscience. 2012, 9 (4) 597-601
76. Monajjemi, M. Struct. Chem, 2012, 23 551.
77. Jon M. Matxain. Jesus M. Ugalde.; M. D. Towler. and R. J. Needs. J. Phys. Chem. A 2003, 107, 10004-10010
78. WU Haishun.XUXiaohong, JIAO Haijun, ZhangFuqiang .; JIA Jianfeng. Chinese Science Bulletin.2003, 48, 11 1102 1107
79. Monajjemi, M . Ketabi ,S.Amiri, A. Russian Journal of Physical Chemistry , 2006, 80 (1), S55-S62
80. M. Monajjemi . Robert Wayne Jr, J.E. Boggs, Chemical. Physics. 2014, 433,1-11
81. Jon M. Matxain. Jesus M. Ugalde. M. D. Towler.and R. J. Needs. J. Phys. Chem. A 2003, 107, 10004-10010
82. WU Haishun. XU iaohong. JIAO Haijun, ZHANG Fuqiang . JIA Jianfeng Chinese Science Bulletin.2003,48 (11),  1102 1107
83. Monajjemi , M. Honarparvar, B. Monajemi, H.Journal of the Mexican Chemical Society, 2006, 50 (4), 143-148
84. Monajjemi ,M. Mollaamin ,F. Journal of Computational and Theoretical Nanoscience,2012 ,9 (12) 2208-2214
85. Monajjemi, M.Mahdavian, L. Mollaamin, F. Honarparvar, B. Fullerenes, Nanotubes and Carbon Nanostructures, 2010,18, 45–55
86. Friedrich, B. J.D. Weinstein. R. Decarvalho . J.M. Doyle. Trap. J. Chem. Phys. 1999,110,2376-2383.
87. Ramsay, N.E. Magnetic Shilding of Nuclei. J. Phys. Rev.1950, 78, 699-703.
88. Frischend, M.J. J.B. Foresman,. Gaussian 94 user’ reference (Gaussian, Inc., Pittsburgh). 1995
89. Ghalandari, B. Monajjemi, M. Mollaamin, F. Journal of Computational and Theoretical Nanoscience, 2011,8, 1212–1219
90. Monajjemi , M.Khosravi , M. Honarparvar, B. Mollaamin, F. International Journal of Quantum Chemistry, 2011, 111, 2771–2777
91. Monajjemi, M. Rajaeian, E.  Mollaamin, F. Physics and Chemistry of Liquids,2008, 46, 299.
92. Tahan, A .Monajjemi, M. Acta Biotheor,2011, 59, 291–312
93. Monajjemi, M. Farahani, N. Mollaamin, F. Physics and Chemistry of Liquids 2012, 50(2) 161–172
94. Monajjemi, M.Razavian, M.H.  Mollaamin,F.  Naderi,F.  Honarparvar,B. Russian Journal of Physical Chemistry A , 2008 , 82 (13),  2277-2285
95. Mollaamin , F.  Varmaghani , Z. Monajjemi , M, Physics and Chemistry of Liquids. 2011,49, 318
96. Monajjemi, M. Honarparvar, B. H. Haeri, H. Heshmat, M. Russian Journal of Physical Chemistry C, 2008, 80(1),S40-S44.
97. Cheeseman, J.R. M.J. Frisch. F.J. Devlin .P.J.Stephens, Chemical Physics Letters, 1996,252 (3-4), 211-220.
98. Naghsh,F, oriental journal of chemistry, 2015, 31(1)
99. Chitsazan, A,oriental journal of chemistry, 2015, 31(1)
100. Frisch, M.J., Trucks, G.W., Schlegel, H.B., Scuseria, G.E., Robb, M.A., Cheeseman, J.R., Montgomery, J.A., Vreven, T., Kudin, K.N., Burant, J.C., Millam, J.M., Iyengar, S.S., Tomasi, J., Barone, V., Mennucci, B., Cossi, M., Scalmani, G., Rega, N., Petersson, G.A., Nakatsuji, H., Hada, M., Ehara, M., Toyota, K., Fukuda, R., Hasegawa, J., Ishida, M., Nakajima, T., Honda, Y., Kitao, O., Nakai, H., Klene, M., Li. X., Knox, J.E., Hratchian, H.P., Cross, J.B., Bakken, V., Adamo, C., Jaramillo, J., Gomperts, R., Stratmann, R.E., Yazyev, O., Austin, A.J., Cammi. R., Pomelli, C., Ochterski, J.W., Ayala, P.Y., Morokuma, K., Voth, G.A., Salvador, P., Dannenberg, J.J., Zakrzewski, V.G., Dapprich, S., Daniels, A.D., Strain, M.C., Farkas, O., Malick, D.K., Rabuck, A.D., Raghavachari, K., Foresman, J.B., Ortiz, J.V., Cui, Q., Baboul, A.G., Clifford, S., Cioslowski, J., Stefanov, B.B., Liu, G., Liashenko, A., Piskorz, P., Komaromi, I.,Martin, R.L., Fox, D.J., Keith, T., Al-Laham, M.A., Peng, C.Y., Nanayakkara, A., Challacombe, M., Gill, P.M.W., Johnson, B., Chen, W., Wong, M.W., Gonzalez, C., and Pople, J.A., Gaussian 03, Revision B.03, Gaussian, Inc, Wallingford CT (2004).

---

This work is licensed under a Creative Commons Attribution 4.0 International License.