Potentiometric studies and theoretical calculations of Some azo rhodanines and their metal complexes

Introduction

Potentiometric titrations are the most useful techniques to investigate equilibrium in solutions and to determine dissociation constants. The potentiometric titration is used due to the simplicity of equipment and minimal time requirements. Rhodanine and its derivatives has attracted special interest due to their inhibition of mycobacterium tuberculosis [1] and as potential medicinal preparations [2]. Azo compounds based on rhodanine play a central role as chelating agents for a large number of metal ions, as they form a stable six-membered ring after complexation with the metal ion and can also be used as analytical reagents [3]. In continuation to the previous work [4-7], we report herein the synthesis of 3-phenylazo-2-thioxo-4-thiazolidinone derivatives. Molecular and electronic structures of the ligands have been discussed. The stability constants of the binary complexes of Cd²⁺, Fe²⁺, Fe³⁺, UO₂²⁺ and Zr⁴⁺ with azo rhodanines were determined from potentiometric titrations data at different temperatures and constant ionic strength of 0.1 M KCl according to Irving-Rossotti’s method. The substituent effects on the dissociation and stability constants of the binary complexes were also investigated. Furthermore, the corresponding thermodynamic functions of the dissociation and complexation are evaluated and discussed.

Experimental

Measurements

All the compounds and solvents used were purchased from Aldrich and Sigma and used as received without any further purification. Elemental microanalyses of the separated compounds for C, H, N and S were determined on Automatic Analyzer CHNS Vario ELIII, Germany. The pH measurements were performed with a Metrohm 836 Titrando (KF& Potentiometric Titrator) equipped with a combined porolyte electrode. The electrode system was calibrated according to the method of Irving et al. [8]. The pH–meter readings in the non–aqueous medium were corrected [9]. The temperature was controlled by circulating thermostated water bath (Neslab 2 RTE 220) through the outer jacket of the vessel within ± 0.05 ^oC.

Preparation of 3-(4`-phenylazo derivatives)-2-thioxo-4-thiazolidinone (HL_n)

The organic compounds (Scheme 1) 3-(4`-phenylazo derivatives)-2-thioxo-4-thiazolidinone (H₂L₁ and H₂L₂) were prepared prviously [5] by gradual addition of an aqueous solution of 0.01 mole of NaNO₂ to a concentrated HCl solution of 0.01 mole of sulphadiazine, sulphamethazine and sulphamethoxazole in the ice bath. The formed diazonium chloride solutions were added gradually with vigrous stirring to a 0.01 mole cold solution of 3-phenyl-2-thioxo-4-thiazolidinone in 40 ml pyridine. After dilution, the compounds (H₂L₁ and H₂L₂) formed were filtered off and washed with water. The crude materials were recrystallized from ethanol and then dried in a vacuum desiccator over anhydrous CaCl₂.

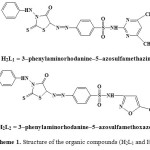Scheme 1: Structure of the organic compounds (H2L1 and H2L2).   Click here to View scheme

 

Potentiometric Measurements

The solutions of 1.0 M KCl and 0.01 M HCl were also prepared in double distilled water. The solution of the organic compound (0.001 M) was prepared by dissolving the accurate weight of the solid in DMF. Metal ion solutions (0.0005 M) were prepared from metal chlorides in double distilled water and standardized with EDTA [10]. Oxalic acid solution was used as a titrant for the standardization of sodium hydroxide solution in 40 % (by volume) DMF–water mixture.

The general conditions, apparatus and methods of calculation were the same as in the previous work [5-7]. The experimental procedure involved the potentiometric titrations of the solutions at 298 K against standard 0.02 M NaOH in 40 % (by volume) DMF–water mixture are listed below:

1. 5 ml 0.01 M HCl + 5 ml 1 M KCl + 20 ml DMF.
2. 5 ml 0.01 M HCl + 5 ml 1 M KCl + 15 ml DMF + 5 ml 0.00l  M ligand.
3. 5 ml 0.01 M HCl + 5 ml l M KCl + 15 ml DMF + 5 ml 0.001 M ligand + 5 ml 0.0005 M metal salt.

The total volume was made up to 50 ml with double distilled water before the titration. The titrations were carried out in an inert atmosphere by pubbling purified nitrogen through the solutions. All the potentiometric titrations were made over the pH range 4.0–11.0. These titrations were repeated for the temperatures of 308 and 318 K.

The molecular structures of the investigated compounds are optimized by HF method with 3-21G basis set. The molecules were built with the Perkin Elmer ChemBio Draw and optimized using Perkin Elmer ChemBio3D software [7].

Results and Discussion

Proton-ligand stability constants

From the titration curves of HCl in the absence and presence of ligands (H₂L₁ and H₂L₂) the average proton-ligand formation number associated with ligands (H₂L_n) at various pH values,`n_A, were calculated by applying the following equation as Irving and Rossotti’s method [11]:

 

where, N° is the concentration of sodium hydroxide solution, V₁ and V₂ are the volumes of alkali required to reach the same pH on the titration curve of hydrochloric acid and reagent, respectively. TC°_L is the total concentration of the reagent, E° is the initial concentration of the free acid. Y is the number of available protons in the azo compounds (Y=1), V° is the initial volume (50 ml) of the mixture. The formation curves (`n<sub>A</sub> vs. pH) for the proton-ligand systems were constructed and found to extend between 0 and 2 in the`n_A scale. This means that the compounds have two dissociable protons (the enol of the sulfonamide group, pK₁^H and carbonyl oxygen in the rhodanine moiety, pK₂^H) [12]. At the same volume of NaOH added the compound titration curves showed a lower pH values than the titration curve of the free acid. The displacement of a compound titration curve along the volume axis with respect to the free acid titration curve is an indication of proton dissociation. The dissociation constants were calculated using Irving and Rossotti’s method [11]. The dissociation constant of –OH group of rhodanine moiety (pK₂^H ) should be higher than that of the sulfonamide group (pK₁^H ) due to the weakly acidic of the phenolic –OH group (i.e,  stronger bonding between the proton and the oxygen donor) [13].

The pK^H values of azorhodanine compounds (Table 1) are influenced by the inductive effect of the substituents. Electron-donating group increase the electron density due to their high positive inductive effect, whereby stronger O–H bond in the sulfonamide group is formed [13]. The suggested three types of tautomerism (Scheme 2) are:

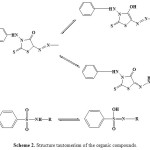Scheme 2: Structure tautomerism of the organic compounds.   Click here to View scheme

 

Metal-ligand stability constants

The formation curves for the binary metal complexes were obtained by plotting the average metal-ligand formation number (`n ) versus the free ligand exponent (pL), according to Irving and Rossotti’s[14]. The free ligands exponent, pL and the average number of the reagent molecules attached per metal ion,`n, can be calculated using eqs. 2 and 3:

 

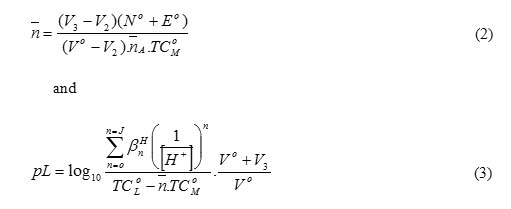
where TC°_M  is the total concentration of the metal ion present in the solution and β^H_n is   the overall proton-ligand stability constant. V₁, V₂ and V₃ are the volumes of alkali required to reach the same pH on the titration curves of hydrochloric acid, azorhodanine compound and binary complex, respectively. These curves were analyzed and the successive stability constants were determined using different computational methods [15,16]. The following general remarks according to the values in Table 2 are:

1. For the binary complexes, the maximum value of`n was » 2 indicating the formation of 1:1 and 1:2 (metal:ligand) complexes only.
2. No possibility of formation of polynuclear complexes, due to the metal ion solution was very dilute (5 x 10^-5 M) [17].
3. The metal titration curves were displaced to the right-hand side of the ligand titration curves along the volume axis, indicating proton release upon complex formation of the metal ion with the azo compound. The large decrease in pH for the metal titration curves relative to ligand titration curves point to the formation of strong metal complexes[18].
4. During the potentiometric titrations, the colour of the solution after complex formation was observed to be different from the colour of the ligand.
5. For the same ligand, the stability of the binary complexes increases in the order Fe²⁺< Cd²⁺< Fe³⁺< UO₂²⁺< Zr⁴⁺ [17,18]. This order largely reflect the changes in the heat of complex formation across the series from a combination of the crystal-field stabilization energies [19] and the influence of both the polarizing ability of the metal ion [20].

Effect of temperature

The dissociation constants (pK^H) for the azorhodanine compounds (H₂L₁ and H₂L₂), as well as the stability constants of their complexes with Cd²⁺, Fe²⁺, Fe³⁺, UO₂²⁺ and Zr⁴⁺ have been evaluated at 298, 308 and 318 K, and are given in Tables 1 and 2. The values of enthalpy change, ∆H, for the dissociation and binary complex process was calculated from the slope of the plot pK^H or log K vs. 1/T using the graphical representation of Van’t Hoff eqs. 4 and 5 (Figs. 1 and 2):

Figure 1: Van’t Hoff plot pKH of H2L1 against 1/T.   Click here to View figure

 

Figure 2: Van’t Hoff plot pKH of H2L2 against 1/T.   Click here to View figure

 

Table 1: Thermodynamic functions for the dissociation of ligands (H₂L₁ and H₂L₂) in 40 % (by volume) DMF-water mixture and 0.1 M KCl at different temperatures.

Compound	T (K)	Dissociation constant   pK1H       pK2H		DG  (kJ.mol-1)      DG1          DG2		DH  (kJ.mol-1)  – DH1        – DH2		DS  (J.mol-1.K-1) -DS1           -DS2
H2L1	298 308 318	7.31 7.16 7.02	9.36 9.19 9.03	41.70 42.22 42.74	53.40 54.19 54.98	26.31	29.94	51.64 51.65 51.66	78.72 78.73 78.74
H2L2	298 308 318	7.15 7.00 6.86	9.53 9.38 9.24	40.79 41.28 41.76	54.37 55.31 56.26	26.31	26.31	48.59 48.60 48.58	94.16 94.15 94.18

 

 

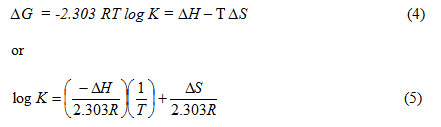
Where, R gas constant = 8.314 J.mol^-1K^-1. K is the dissociation constant for the ligand stability, T is the temperature (K).

The entropy ∆S can be calculated from the ∆G and ∆H values, using the well known relationships 4 and 6:

∆ S = (∆H – ∆G) / T           (6)

The thermodynamic parameters of the dissociation process of the azorhodanine compounds (H₂L₁ and H₂L₂) are recorded (Table 1). The following general remarks can be pointed out:

1. The protonation constants of each ligand decreased with increasing temperature (Table 2). Therefore corresponding enthalpy changes are exothermic, i.e, the lower temperature is favorable for protonation of all the ligands.
2. A positive value of DG indicates that the dissociation process is not spontaneous [21].
3. The DS values for the dissociation process are negative, confirming that the dissociation is entropically unfavorable.

Table 2: Stepwise Stability Constants for ML and ML₂ Complexes of H₂L₁ and H₂L₂ in 40 % (by volume) DMF-Water Mixtures and 0.1 M KCl at different temperatures.

Compound	Mn+	298 K		308 K		318 K
		log K1	log K2	log K1	log K2	log K1	log K2
H2L1	Fe2+	7.42	5.23	7.58	5.39	7.73	5.54
	Cd2+	7.76	5.85	7.93	6.00	8.09	6.14
	Fe3+	7.95	5.97	8.12	6.13	8.27	6.28
	UO22+	8.10	6.16	8.27	6.32	8.43	6.46
	Zr4+	8.46	6.31	8.59	7.26	8.75	6.63
H2L2	Fe2+	6.41	5.15	6.56	5.31	6.70	5.46
	Cd2+	7.08	5.67	7.25	5.82	7.42	5.96
	Fe3+	7.28	5.73	7.43	5.88	7.57	6.02
	UO22+	7.50	5.91	7.66	6.06	7.82	6.21
	Zr4+	7.83	6.21	7.98	6.36	8.13	6.50

 

Table 3:  Thermodynamic Functions for ML and ML₂ Complexes of H₂L₁ and H₂L₂ in 40 % (by volume) DMF-Water Mixture and 0.1 M KCl at 298 K.

Compound	Mn+	DG (kJ.mol-1)		DH  (kJ.mol-1)		DS (J.mol-1.K-1)
		– DG1	– DG2	DH1	DH2	DS1	DS2
H2L1	Fe2+	42.33	29.84	28.13	28.13	236.44	194.53
	Cd2+	44.27	33.37	29.94	26.31	249.02	200.26
	Fe3+	45.36	34.06	29.03	28.13	249.63	208.69
	UO22+	46.21	35.14	29.94	27.22	255.53	209.26
	Zr4+	48.27	36.00	26.31	29.03	250.26	218.22
H2L2	Fe2+	36.57	29.38	26.31	28.13	211.00	192.98
	Cd2+	40.39	32.35	30.85	26.31	239.06	196.84
	Fe3+	41.53	32.69	26.31	26.31	227.65	197.98
	UO22+	42.79	33.72	29.03	27.22	241.01	204.49
	Zr4+	44.67	35.43	27.22	26.31	241.24	207.18

 

The thermodynamic parameters of the stepwise stability constants of binary complexes are recorded (Table 3). It is known that the divalent metal ions exist in solution as octahedrally hydrated species [15]. The obtained values of DH and DS can then be considered as the sum of the contributions of release of H₂O molecules and metal-ligand bond formation. Examination of these values shows that:

 

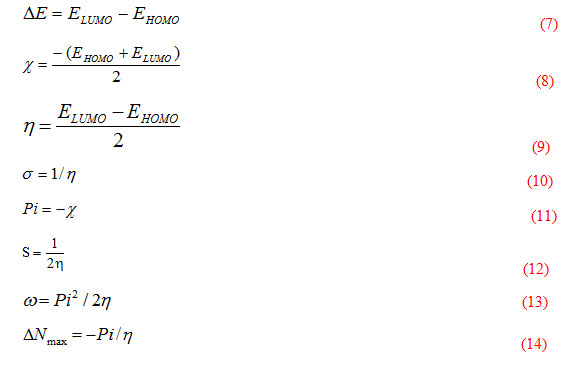
Table 4: The selected geometric parameters for H₂L₁.

C(34)-H(53) 1.114 C(34)-H(52) 1.114 C(34)-H(51) 1.113 C(33)-H(50) 1.114 C(33)-H(49) 1.114 C(33)-H(48) 1.114 C(30)-H(47) 1.1 N(26)-H(46) 1.051 C(22)-H(45) 1.103 C(21)-H(44) 1.103 C(19)-H(43) 1.103 C(18)-H(42) 1.105 C(14)-H(41) 1.103 C(13)-H(40) 1.103 C(12)-H(39) 1.103 C(11)-H(38) 1.103 C(10)-H(37) 1.104 N(8)-H(36) 1.051 O(7)-H(35) 0.972 C(31)-N(32) 1.264 C(27)-N(32) 1.27 N(28)-C(27) 1.271 C(29)-N(28) 1.265 C(30)-C(29) 1.34 C(31)-C(30) 1.34 C(17)-C(22) 1.347 C(21)-C(22) 1.343 C(20)-C(21) 1.344 C(19)-C(20) 1.343 C(18)-C(19) 1.342 C(17)-C(18) 1.347 C(9)-C(14) 1.346 C(13)-C(14) 1.342 C(12)-C(13) 1.342 C(10)-C(11) 1.342 C(2)-S(3) 1.789 C(4)-S(3) 1.483 C(5)-C(4) 1.356 N(1)-C(5) 1.277 C(2)-N(1) 1.267 C(29)-C(34) 1.507 C(31)-C(33) 1.506 N(26)-C(27) 1.274 S(23)-N(26) 1.702 S(23)-O(25) 1.457 S(23)-O(24) 1.457 C(20)-S(23) 1.801 N(16)-C(17) 1.269 N(15)-N(16) 1.252 C(4)-N(15) 1.268 N(8)-C(9) 1.272 N(1)-N(8) 1.356 C(5)-O(7) 1.365 C(2)-S(6) 1.574

H(50)-C(33)-H(49) 108.243 H(50)-C(33)-H(48) 107.225 H(50)-C(33)-C(31) 111.964 H(49)-C(33)-H(48) 108.309 H(49)-C(33)-C(31) 109.844 H(48)-C(33)-C(31) 111.125 N(32)-C(31)-C(30) 119.974 N(32)-C(31)-C(33) 116.924 C(30)-C(31)-C(33) 123.098 H(53)-C(34)-H(52) 108.513 H(53)-C(34)-H(51) 107.615 H(53)-C(34)-C(29) 110.458 H(52)-C(34)-H(51) 107.591 H(52)-C(34)-C(29) 110.46 H(51)-C(34)-C(29) 112.07 H(47)-C(30)-C(29) 121.726 H(47)-C(30)-C(31) 121.315 C(29)-C(30)-C(31) 116.959 N(28)-C(29)-C(30) 120.09 N(28)-C(29)-C(34) 116.334 C(30)-C(29)-C(34) 123.576 C(31)-N(32)-C(27) 120.697 C(27)-N(28)-C(29) 120.526 N(32)-C(27)-N(28) 121.754 N(32)-C(27)-N(26) 121.372 N(28)-C(27)-N(26) 116.874 H(46)-N(26)-C(27) 115.064 H(46)-N(26)-S(23) 118.863 C(27)-N(26)-S(23) 124.607 N(26)-S(23)-O(25) 110.604 N(26)-S(23)-O(24) 110.3 N(26)-S(23)-C(20) 82.563 O(25)-S(23)-O(24) 123.708 O(25)-S(23)-C(20) 110.6 O(24)-S(23)-C(20) 111.535 H(44)-C(21)-C(22) 118.636 H(44)-C(21)-C(20) 120.429 C(22)-C(21)-C(20) 120.934 C(21)-C(20)-C(19) 118.324 C(21)-C(20)-S(23) 120.686 C(19)-C(20)-S(23) 120.982 H(43)-C(19)-C(20) 120.751 H(43)-C(19)-C(18) 118.69 C(20)-C(19)-C(18) 120.558 H(45)-C(22)-C(17) 121.793 H(45)-C(22)-C(21) 117.041 C(17)-C(22)-C(21) 121.165 H(42)-C(18)-C(19) 118.206 H(42)-C(18)-C(17) 120.199 C(19)-C(18)-C(17) 121.595 C(22)-C(17)-C(18) 117.424 C(22)-C(17)-N(16) 125.779 C(18)-C(17)-N(16) 116.797 C(17)-N(16)-N(15) 119.578

H(40)-C(13)-C(14) 120.015 H(40)-C(13)-C(12) 119.845 C(14)-C(13)-C(12) 120.14 H(39)-C(12)-C(13) 120.157 H(39)-C(12)-C(11) 120.156 C(13)-C(12)-C(11) 119.687 H(38)-C(11)-C(12) 119.888 H(38)-C(11)-C(10) 120.044 C(12)-C(11)-C(10) 120.068 H(41)-C(14)-C(9) 121.135 H(41)-C(14)-C(13) 118.322 C(9)-C(14)-C(13) 120.543 H(37)-C(10)-C(11) 118.653 H(37)-C(10)-C(9) 120.715 C(11)-C(10)-C(9) 120.633 C(14)-C(9)-C(10) 118.928 C(14)-C(9)-N(8) 122.978 C(10)-C(9)-N(8) 118.094 N(16)-N(15)-C(4) 119.257 C(2)-S(3)-C(4) 93.397 H(35)-O(7)-C(5) 110.072 S(3)-C(4)-C(5) 110.772 S(3)-C(4)-N(15) 131.765 C(5)-C(4)-N(15) 117.462 H(36)-N(8)-C(9) 115.199 H(36)-N(8)-N(1) 116.684 C(9)-N(8)-N(1) 123.548 C(4)-C(5)-N(1) 116.148 C(4)-C(5)-O(7) 123.104 N(1)-C(5)-O(7) 120.747 C(5)-N(1)-C(2) 114.001 C(5)-N(1)-N(8) 122.372 C(2)-N(1)-N(8) 123.481 S(3)-C(2)-N(1) 105.682 S(3)-C(2)-S(6) 125.061 N(1)-C(2)-S(6) 129.256

 

1. The stepwise stability constants (log K₁ and log K₂) for binary complexes increase with increasing temperature (Figs. 3 and 4). Therefore corresponding enthalpy changes are endothermic, i.e, the higher temperature is favorable for formation of binary complexes.
2. The negative value of DG for the complexation process indicates the spontaneous nature of such process [22].
3. The DS values for the ligand complexes are positive, confirming that the complex formation is entropically favourable [23].

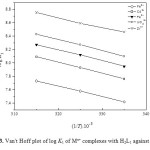Figure 3: Van’t Hoff plot of log K1 of Mn+ complexes with H2L1 against 1/T.   Click here to View figure

 

Figure 4: Van’t Hoff plot of log K1 of Mn+ complexes with H2L2 against 1/T.   Click here to View figure

 

Geometrical structure of the ligands

Molecular structures of the azorhodanine compounds (H₂L₁ and H₂L₂) are optimized by HF method with 3-21G basis set. The calculated molecular structures for H₂L₁ and H₂L₂ ligands are shown in Fig. 5. Selected geometric parameters bond lengths and bond angles of H₂L₁ and H₂L₂ ligands are listed in Tables 4 and 5.

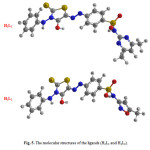Figure 5: The molecular structures of the ligands (H2L1 and H2L2).   Click here to View figure

 

Bond lengths (Å)	Bond angles (o)	Bond angles (o)
C(32)-H(48) 1.114 C(32)-H(47) 1.113 C(32)-H(46) 1.114 C(29)-H(45) 1.097 N(26)-H(44) 1.051 C(22)-H(43) 1.103 C(21)-H(42) 1.103 C(19)-H(41) 1.103 C(18)-H(40) 1.105 C(14)-H(39) 1.103 C(13)-H(38) 1.103 C(12)-H(37) 1.103 C(11)-H(36) 1.103 C(10)-H(35) 1.104 N(8)-H(34) 1.051 O(7)-H(33) 0.972 C(17)-C(22) 1.347 C(21)-C(22) 1.343 C(20)-C(21) 1.343 C(19)-C(20) 1.343 C(18)-C(19) 1.342 C(17)-C(18) 1.347 C(9)-C(14) 1.346 C(13)-C(14) 1.342 C(12)-C(13) 1.341 C(11)-C(12) 1.341 C(10)-C(11) 1.342 C(9)-C(10) 1.345 C(28)-C(29) 1.341 C(30)-C(29) 1.343 N(31)-C(30) 1.267 O(27)-N(31) 1.32 C(28)-O(27) 1.228 C(2)-S(3) 1.789 C(4)-S(3) 1.483 C(5)-C(4) 1.356 N(1)-C(5) 1.277 C(2)-N(1) 1.267 N(26)-C(30) 1.269 C(28)-C(32) 1.499 S(23)-N(26) 1.703 S(23)-O(25) 1.457 S(23)-O(24) 1.457 C(20)-S(23) 1.799 N(16)-C(17) 1.269 N(15)-N(16) 1.252 C(4)-N(15) 1.268 N(8)-C(9) 1.272 N(1)-N(8) 1.356 C(5)-O(7) 1.365 C(2)-S(6) 1.574	H(48)-C(32)-H(47) 108.159 H(48)-C(32)-H(46) 108.544 H(48)-C(32)-C(28) 110.078 H(47)-C(32)-H(46) 108.178 H(47)-C(32)-C(28) 111.696 H(46)-C(32)-C(28) 110.1 C(29)-C(28)-O(27) 110.086 C(29)-C(28)-C(32) 126.208 O(27)-C(28)-C(32) 123.706 N(31)-O(27)-C(28) 106.877 C(30)-N(31)-O(27) 111.773 H(45)-C(29)-C(28) 125.92 H(45)-C(29)-C(30) 127.858 C(28)-C(29)-C(30) 106.222 C(29)-C(30)-N(31) 105.041 C(29)-C(30)-N(26) 128.236 N(31)-C(30)-N(26) 126.721 H(44)-N(26)-C(30) 113.836 H(44)-N(26)-S(23) 117.867 C(30)-N(26)-S(23) 124.175 N(26)-S(23)-O(25) 107.48 N(26)-S(23)-O(24) 106.852 N(26)-S(23)-C(20) 83.868 O(25)-S(23)-O(24) 123.145 O(25)-S(23)-C(20) 113.244 O(24)-S(23)-C(20) 114.278 H(42)-C(21)-C(22) 118.77 H(42)-C(21)-C(20) 120.376 C(22)-C(21)-C(20) 120.853 C(21)-C(20)-C(19) 118.47 C(21)-C(20)-S(23) 120.646 C(19)-C(20)-S(23) 120.881 H(41)-C(19)-C(20) 120.688 H(41)-C(19)-C(18) 118.842 C(20)-C(19)-C(18) 120.47 H(43)-C(22)-C(17) 121.815 H(43)-C(22)-C(21) 117.033 C(17)-C(22)-C(21) 121.152 H(40)-C(18)-C(19) 118.196 H(40)-C(18)-C(17) 120.215 C(19)-C(18)-C(17) 121.589 C(22)-C(17)-C(18) 117.466 C(22)-C(17)-N(16) 125.763 C(18)-C(17)-N(16) 116.771 C(17)-N(16)-N(15) 119.584 H(38)-C(13)-C(14) 120.016 H(38)-C(13)-C(12) 119.845 C(14)-C(13)-C(12) 120.139 H(37)-C(12)-C(13) 120.157 H(37)-C(12)-C(11) 120.151 C(13)-C(12)-C(11) 119.692 H(36)-C(11)-C(12) 119.896 H(36)-C(11)-C(10) 120.038 C(12)-C(11)-C(10) 120.066	H(39)-C(14)-C(9) 121.139 H(39)-C(14)-C(13) 118.323 C(9)-C(14)-C(13) 120.538 H(35)-C(10)-C(11) 118.658 H(35)-C(10)-C(9) 120.712 C(11)-C(10)-C(9) 120.63 C(14)-C(9)-C(10) 118.934 C(14)-C(9)-N(8) 122.996 C(10)-C(9)-N(8) 118.069 N(16)-N(15)-C(4) 119.253 C(2)-S(3)-C(4) 93.394 H(33)-O(7)-C(5) 110.083 S(3)-C(4)-C(5) 110.781 S(3)-C(4)-N(15) 131.744 C(5)-C(4)-N(15) 117.474 H(34)-N(8)-C(9) 115.254 H(34)-N(8)-N(1) 116.754 C(9)-N(8)-N(1) 123.621 C(4)-C(5)-N(1) 116.133 C(4)-C(5)-O(7) 123.113 N(1)-C(5)-O(7) 120.752 C(5)-N(1)-C(2) 114.012 C(5)-N(1)-N(8) 122.369 C(2)-N(1)-N(8) 123.458 S(3)-C(2)-N(1) 105.678 S(3)-C(2)-S(6) 125.059 N(1)-C(2)-S(6) 129.261

 

Molecular structures (HOMO & LUMO) for H₂L₁ and H₂L₂ are presented in Fig. 6. The HOMO–LUMO energy gap (ΔE), which is an important stability index, is applied to develop theoretical models for explaining the structure and conformation barriers in many molecular systems [24,25]. The calculated quantum chemical parameters are given in Table 6. Additional parameters such as separation energies (∆E), absolute electronegativities (χ), chemical potentials (Pi), absolute hardness (η), absolute softness (σ), global electrophilicity (ω) [7], global softness (S), and additional electronic charge (∆N_max), are calculated according to the following equations [26]:

Table 6: The calculated quantum chemical parameters for the ligands (H₂L₁ and H₂L₂).

Compound	EHOMO (eV)	ELUMO (eV)	∆E (eV)	χ (eV)	η (eV)	σ (eV)-1	Pi (eV)	S  (eV)-1	ω (eV)	∆Nmax
H2L1	-2.250	-2.121	0.129	2.186	0.065	15.504	-2.186	7.752	37.026	33.884
H2L2`	-2.251	-2.147	0.104	2.199	0.052	19.231	-2.199	9.615	46.496	42.288

 

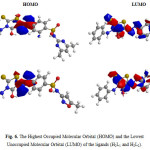Figure 6: The Highest Occupied Molecular Orbital (HOMO) and the Lowest Unoccupied Molecular Orbital (LUMO) of the ligands (H2L1 and H2L2).   Click here to View figure

 

The azorhodanine compound (H₂L₂) is more reactive than azorhodanine compound (H₂L₁) as reflected from energy gap values (Table 6). The value of ∆E for ligands H₂L₁ and H₂L₂ is found 0.129 and 0.104 e.V, respectively.

References

1. A.Z. El-Sonbati, M.A. Diab, A.A. El-Bindary, G.G. Mohamed, S.M. Morgan,  Thermal, spectroscopic studies and hydrogen bonding in supramolecular assembly of azo rhodanine complexes, Inorg. Chim. Acta 430 (2015) 96.
2. F.C. Brown, C.K. Bradsher, B.F. Moser and S. Forrester, Studies of the synthesis of bicyclo[2.2.0] hexane and certain reactions of 3-benzhydrylcyclopentene-4-carboxylic acid  J. Org. Chem. 24 (1959) 1056.
3. A.C. Fabretti and G. Peyronel, Siver(I) and Gold(I) complexes of rhodanine, Transition Met. Chem. 2 (1977) 224.
4. A.A. El-Bindary, A.Z. El-Sonbati, M.A. Diab, E.E. El-Katori, H.A. Seyam. Potentiometric and Thermodynamic Studies of Some Schiff-base Derivatives of 4-Aminoantipyrine and Their Metal Complexes, Int. J. Adv. Res., 2(4) (2014) 493.
5. A.Z. El-Sonbati, A.A. El-Bindary and R.M. Ahmed, Potentiometric and conductometric studies on the complexes of some rare earth metals with rhodanine azosulfonamide derivatives. XII, J. Sol. Chem. 32 (2003) 617.
6. A.Z. El-Sonbati, A.A. El-Bindary, S.A. Abd El-Mksoud, A.A.M. Belal, R.A. El-Boz, Spectroscopic, potentiometric and thermodynamic studies of azo rhodanines and their metal complexes, J. Mol. Liq. 199 (2014) 538.
7. A.A. El-Bindary, A.Z. El-Sonbati, M.A. Diab, Sh.M. Morgan, Geometrical structure, potentiometric and thermodynamic studies of rhodanine azodye and its metal comlexes, J. Mol. Liq. 201 (2015) 36.
8. H.M. Irving, M.G. Miles, L.D. Pettit, A study of some problems in determining the stoicheiometric proton dissociation constants of complexes by potentiometric titrations using a glass electrode, Anal. Chim. Acta 38 (1967) 475.
9. R.G. Bates, M. Paabo, R.A. Robinson, Interpretation of pH measurements in alcohol-water solvents, J. Phys. Chem. 67 (1963) 1833.
10. G. H. Jeffery, J. Bassett, J. Mendham and R. C. Deney, “Vogel’s Textbook of Quantitative Chemical Analysis”, 5^th Edn., Longman, London, 1989.
11. K. Irving and H.S. Rossotti, The calculation of formation curves of metal complexes from pH titration curves in mixed solvents, J. Chem. Soc. (1954) 2904.
12. B.A. El-Shetary, S.L. Stefan, F.I. Zidan and S.B. El-Maraghy, Determination of stability constants of some substituted 4-pyrazolone dyes containing o-methoxy, o-carboxy and o-nitro groups with trivalent lanthanide ions, Monatsh.Chem. 118 (1987) 1101.
13. V.D. Athawale and S.S. Nerkar, Stability constants of complexes of divalent and rare earth metals with substituted salicynals, Monatsh. Chem. 131 (2000) 267.
14. K. Irving and H.S. Rossotti, Methods for computing successive stability constants from experimental formation curves, J. Chem. Soc. (1953) 3397.
15. F.I.C. Rossotti and H.S. Rossotti, Graphical methods for determining equilibrium constants. I. Systems of mononuclear complexes, Acta Chem. Scand. 9 (1955) 1166.
16. M.T. Beck and I. Nagybal, “Chemistry of Complex Equilibrium”, Wiley, New York, 1990.
17. P. Sanyal and G.P. Sengupta, Potentiometric studies of complex-formation of some trivalent rare-earths with p,p’-bromosulphonosalicylidene, J. Ind. Chem. Soc. 67 (1990) 342.
18. V.D. Athawale and V. Lele, Stability constants and thermodynamic parameters of complexes of lanthanide ions and (±)-norvaline, J. Chem. Eng. Data. 41(1996) 1015.
19. F.R. Harlly, R.M. Burgess and R.M. Alcock, “Solution Equilibria”, P. 257, Ellis Harwood, Chichester, 1980.
20. G.A. Ibañez and G. M. Escandar, Complexation of cobalt(II), nickel(II) and zinc(II) ions with mono and binucleating azo compounds: A potentiometric and spectroscopic study in aqueous solution, Polyhedron 17 (1998) 4433.
21. C.S.G. Phillips and R. J. P. Williams, Inorganic Chemistry: Metals, Vol. 2, P. 268, Oxford University Press, New York, NY, USA, 1966.
22. A.T. Mubarak, A.Z. El-Sonbati, A.A. El-Bindary, Potentiometric and conductometric studies on the complexes of some transition metals with rhodanine azosulfonamide derivatives XI, Chem. Pap. 58 (2004) 320.
23. A. Bebot-Bringaud, C. Dange, N. Fauconnier and C. Gerard, NMR, potentiometric and spectrophotometric studies of phytic acid ionization and complexation properties toward Co²⁺, Ni²⁺, Cu²⁺, Zn²⁺ and Cd²⁺, J. Inorg. Biochem. 75 (1999) 71.
24. N.A. El-Ghamaz, A.Z. El-Sonbati, M.A. Diab, A.A. El-Bindary, G.G. Mohamed, Sh.M. Morgan, Correlation between ionic radii of metal azodye complexes and electrical conductivity, Spectrochim. Acta A. 147 (2015) 200.
25. N.A. El-Ghamaz, A.Z. El-Sonbati, M.A. Diab, A.A. El-Bindary, M.K. Awad, Sh.M. Morgan, Dielectrical, conduction mechanism and thermal properties of rhodanine azodyes, Mater. Sci. Semicond. Process. 19 (2014) 150.
26. A.Z. El-Sonbati, A.F. Shoair, A.A. El-Bindary, A.S. Mohamed, Synthesis, characterization, DNA binding and catalytic activities of Ru(III) complexes, J. Mol Liq. 209 (2015) 635.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.