Density functional theory (B3LYP/6-311+G**) study of some semicarbazones formation mechanism

Introduction

Nitrogen containing compounds are very widely distributed in nature and are essential to life, playing a vital role in the metabolism of all living cells. Presently, over 70 % drugs incorporate imine functionality, and these compounds owe their bioactivities to the nitrogen-containing units [1]. The most promising and convenient synthetic route for these chiral nitrogen-containing building blocks is the use of imines as electrophiles [2].  Although the synthesis of these nitrogen-containing compounds by the easily available imine is one of the most important and convenient routes, as compared with the counterpart C=O bond, C=N bond is a less explored area. This stereo selectivity of imines has been used in the synthesis of peptidic antibiotics as well as other biologically active molecules. In pharmaceutical and agro allied industries, enantio-selectivity of imines has been extensively employed, e.g. in the synthesis of chiral herbicide (S)–Metolachlor [3]. Over the years there has been a keen interest in developing new applications of imine chemistry that enable the facile construction of the nitrogen heterocyclic frameworks found in alkaloids and other biologically active nitrogen heterocycles [4].  Semicarbazones are of much interest due to their wide spectrum of pharmacological activities, recently studies have shown that they exhibit anticonvulsant [5], analgesic, anti-inflammatory properties etc. [6].  Antipyretic activity of synthesized 4-methylphenylsemicarbazone derivatives has also been investigated by [7].

Computational Methodology

The geometries of the reactants, various intermediates, transition states and products were optimized using the hybrid density functional theory, i.e., Becke’s three-parameter nonlocal exchange functional with the nonlocal correlation functional of Lee, Yang, Parr (B3LYP) [8]^.  For systems involving heavy atoms, the B3LYP/6-311+G** level of theory is a balanced choice of method for computational efficiency and accuracy, and spin contamination issue is suppressed effectively by this method [9]. Zero-point energies and harmonic vibrational frequencies were calculated at the B3LYP/6-311+G** level with the optimized geometries. The intermediates were characterized by all the real frequencies, while the transition states were characterized by one imaginary frequency. Intrinsic reaction coordinate (IRC) calculations at the B3LYP/6-311+G** level were used to confirm connections of transition state between two local minima [10]. In finding the most likely geometries of all saddle points, no arbitrary assumptions were made [11]. The energies of all the stationary points were calculated using thermochemical recipe at T1 theory level which is a composite scheme based on single-point energies, i.e., RRIMP2(FC/ 6-311++G(2df,2p)[6-311G*]. All the ab initio calculations were carried out using SPARTAN 8 and 14 packages.

Results and Discussion

In all the five system investigated, the reaction mechanism involves two transition and an intermediate elementary steps. The mechanism is a two-step reaction pathway.

The general reaction mechanism for reaction between acetophenone and semicarbazide is as presented in Figure 1 below.

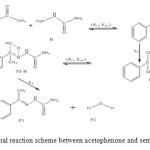Figure 1: General reaction scheme between acetophenone and semicarbazide.  Click here to View figure

 

In the transition state reaction scheme, the first step involving C=O, N–H partial cleavage, C–N and O–H partial bonding is found to have activation energy of 50 kJ/mol.  This in turn forms the intermediate through an endothermic (+27 kJ/mol) [12] and non-spontaneous step (+79 kJ/mol) in Figures 2 and 3 respectively.  Next the intermediate, through intra-molecular interaction, in turn forms the second transition state (TSII) which eventually disappears to form the products. This endothermic and non-spontaneous transformation is accomplished through C=N, O–H bond formation and N–H bond cleavage with energy barrier of 187 kJ/mol as seen respectively in Figures 2 and 3 below. The two-step reaction mechanism presented by the potential and free energies profiles shows that the overall transformation is endothermic (+122 kJ/mol) and slightly non-spontaneous (+1 kJ/mol). The first consecutive (bimolecular) step is found to be the rate determining step. The geometrical variations of the transition states and intermediate during the course of reaction are as presented in Tables 1 and 2 below, while Tables 3 and 4 respectively show thermodynamic and kinetic parameters for the reaction.

Table 1: Variations in bond distances during transformation through TSI, INT and TSII 

TSI	Bond Length (A0)	INT	Bond Length (A0)	TSII	Bond Length (A0)
C2,C7	1.526	C2,C7	1.540	C2,C7	1.469
C7,C8	1.523	C7,C8	1.526	C7,C8	1.491
C7,O1	1.345	C7,O1	1.430	C7,O1	2.301
O1,H10	1.359	O1,H8	0.963
N1,H10	1.206
C7,N1	1.697	C7,N1	1.484	C7,N1	1.346
N1,H2	1.021
N1,N2	1.404	N1,N2	1.397	N1,N2	1.411

 

Table 2: Variations in bond distances during transformation through TSI, INT and TSII 

TSI		INT		TSII
C2C7O1	115.85			C5O1H8	53.10̊
C2O1H3	79.14̊	C5O1H11	108.39̊	N1H8O1	112.42̊
N1C2O1	92.13̊	N1C5O1	112.01̊	N1C5O1	71.98̊
O1H3N1	115.48̊
		C5N1H8	111.79̊	C5N1H8	105.46̊
		C6C5N1	109.58̊	C6C5N1	121.06̊
		C4C5N1	108.39̊	C4C5N1	119.10̊

 

It can be seen that there is an increase of about 0.014  in C2-C7 bond length as the reaction proceeds from TS1 to INT, while the same bond length decreases by 0.071  proceeding from INT to TSII. Similar trend was observed in C7-C8 bond order as the reaction progresses from the first transition state through intermediate to the second transition state.  However, there is a progressive increase in bond length (for C7-O1) from the first transition state to the second transition state in the magnitude of 0.085  at intermediate and 0.871 at TSII in readiness for C7-O1 bond fission in the final product. In the same vein, C7-N1 bond length experiences decrease progressively from TSI through INT to TSII (with 0.213   from TSI to INT and 0.138  from INT to TSII) characteristic of double bond. It can also be seen that N1-N2 remains almost unchanged as it is relatively far away from the reactive site. Similar trends were also observed in bond angles as the molecules undergo transformation through the stationary points to the product.

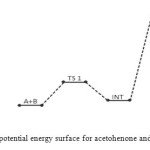Figure 2: Profiles of the potential energy surface for acetohenone and semicarbazide reaction.  Click here to View figure

 

Figure 3: Profiles of the Gibbs free energy for acetohenone and semicarbazide reaction.  Click here to View figure

 

Table 3: DFT B3LYP (6-311+G**) Thermodynamic parameters for acetophenone and semicarbazide reaction at 298.15 K

	ΔfH0(kJ mol-1)	S0(Jmol-1K-1)	G0(kJ mol-1)	Ee(kJ mol-1)
A	-86.47	351.05	-1010545.65	-1010822.21
B	-107.46	307.13	-736799.88	-736937.45
TSI	-221.97	447.25	-1747118.51	-1747708.73
INT	-223.27	443.20	-1747266.86	-1747749.68
TSII	-243.42	455.10	-1747099.61	-1747566.42
P1	+16.29	422.26	-1546612.34	-1547023.23
P2	-237.59	188.86	-200732.23	-200611.72

 

Table 4: DFT B3LYP (6-311+G**) Calculated kinetic Parameters for acetophenone and semicarbazide reaction at 298.15 K

Steps	k2    (dm3mol-1s-1)	k1 (s-1)	K2	K1	A       (dm3mol-1s-1)
A + B TSI			7.84 10-7		4.4
A+B INT	4.87 106
INT TSII				1.42 104	70.65 1012
INT P1+P2		8.84 1016

 

The general reaction mechanism for reaction between cyclohexanone and semicarbazide is as presented in Figure 4 below.

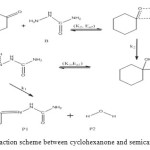Figure 4: General reaction scheme between cyclohexanone and semicarbazide.  Click here to View figure

 

The bimolecular transition step leading to the first activated complex (TSI) is computed to be non-spontaneous (161 kJ/mol) Figure 6 belowe. This transition is accomplished through intermolecular engagement involving C=O bond partial cleavage, O–H and C–N partial bond formation. It’s also associated with very high energy barrier of 168 kJ/mol. The pre-exponential factor and equilibrium values are very small as only few of the reacting molecules is energized enough to overcome the activation energy for this step. The TSI then forms slightly less stable (relative to the two reacting molecules) intermediate [13]. The bimolecular consecutive step slightly non-spontaneous and exothermic (+4 kJ/mol and –8 kJ/mol respectively, it is found to be the rate determining step the value of which is presented in Table below. The resulting intermediate further undergoes intra-molecular interaction through second transition state (TSII) involving C=N partial formation and C–O and H–N partial cleavage as presented in the Table below to form the products. The products (P1+P2) has stabilization energy of (–66 kJ/mol) relative to the starting molecules, indicating that the two-step mechanism is largely spontaneous and slightly exothermic by –12 kJ/mol. The unimolecular consecutive step has barrier height of 99 kJ/mol,which makes it much faster than the preceding bimolecular consecutive step. The geometrical variations of the transition states and intermediate during the course of reaction are as presented in Tables 5 and 6 below, while Tables 7 and 8 respectively show thermodynamic and kinetic parameters for the reaction.

Table 5: Variations in bond distances during transformation through TSI, INT and TSII 

TSI	Bond Length (A0)	INT	Bond Length (A0)	TSII	Bond Length (A0)
C1,C6	1.527	C1,C6	1.540	C1,C6	1.500
C5,C6	1.529	C5,C6	1.533	C5,C6	1.502
C6,O1	1.340	C6,O1	1.432	C6,O1	3.617
C6,N1	1.729	C6,N1	1.473	C6,N1	1.282
O1H1	1.340	O1H11	0.964
N1,N2	1.404	N1,N2	1.425	N1,N2	1.368
		N1H13	1.021	N1H13	1.140

 

One observes that as the reaction proceeds from first transition state to the intermediate, C1-C6 bond length increases by 0.013 , but decreases by 0.040  on getting to the second transition state. C5-C6 bond length was found to undergo similar variations as the reaction progresses from TSI through INT to TSII. It was also seen that C6-O1 bond order experiences increase progressively from TSI to TSII preparatory for the bond fission in the final product.  C6-N1 bond length progressively decreases by 0.256  at INT and 0.191  at TSII leading to double bond formation in the final product [14]. While the bond angle C5C6O1 decreases by 35.58 ̊, C1C6O1 increases by 10.04 ̊as the system transforms from TSI to TSII. Similar increases were seen for C5C6N1, C5C6N1 and C6N1N2, moving from TSI through INT to TSII.

Table 6: Variations in bond angles during transformation through TSI, INT and TSII

TSI		INT		TSII
<C5C6O1	115.66 ̊	<C5C6O1	106.31 ̊	<C5C6O1	80.08 ̊
<C1C6O1	116.55 ̊	<C1C6O1	110.26 ̊	<C1C6O1	126.59 ̊
<C5C6C1	113.32 ̊	<C5C6C1	110.77 ̊	<C5C6C1	116.85 ̊
<N1C6O1	90.72 ̊	<N1C6O1	112.48 ̊	<N1C6O1	61.57 ̊
<C5C6N1	108.35 ̊	<C5C6N1	107.21 ̊	<C5C6N1	118.86 ̊
<C1C6N1	109.43 ̊	<C1C6N1	109.73 ̊	<C1C6N1	124.14 ̊
<C6N1N2	127.19 ̊	<C6N1N2	112.42 ̊	<C6N1N2	130.20 ̊

 

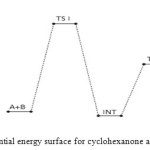Figure 5: Profiles of the potential energy surface for cyclohexanone and semicarbazide reaction.  Click here to View figure

 

Figure 6: Profiles of the Gibbs free energy for cyclohexanone and semicarbazide reaction. Click here to View figure

 

Table 7: DFT B3LYP (6-311+G**) Thermodynamic and kinetic parameters for cyclohexanone and semicarbazide reaction at 298 K

Species	ΔfH0(kJ mol-1)	S0(Jmol-1K-1)	G0(kJ mol-1)	Ee(kJ mol-1)
A	-224.41	325.60	-813541.20	-813856.79
B	-107.46	307.13	-736741.59	-736937.45
TSI	-344.85	426.02	-1550121.59	-1550626.99
INT	-377.86	416.53	-1550278.59	-1550802.90
TSII	-290.85	439.05	-1550204.55	-1550703.40
P1	-124.17	402.04	-1349616.20	-1350064.63
P2	-237.59	189.17	-200732.49	-200741.95

 

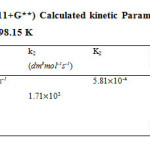Table 8: DFT B3LYP (6-311+G**) Calculated kinetic Parameters for cyclohexanone and semicarbazide reaction at 298.15 K  Click here to View table

 

The general reaction mechanism for reaction between benzyl methyl ketone and semicarbazide is as presented in Figure 7 below.

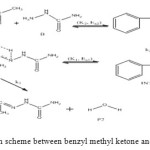Figure 7: General reaction scheme between benzyl methyl ketone and semicarbazide.  Click here to View figure

 

The benzyl methyl ketone and semicarbazide through hydrogen abstraction O–H and C–N bond forms an activated complex (with un-stability of +159 kJ/mol). This transition state disappears to form a more stable (–1 kJ/mol and –160 kJ/mol compared to the starting molecules and the transition state TSI respectively) intermediate. This transformation of the reactants to intermediate has a barrier height of 160 kJ/mol. The intermediate in turn form the respective semicarbazone via a second activated complex with activation energy and relative stability of 197 kJ/mol and –59 kJ/mol. The energetics of the general reaction suggest indicates that the overall mechanism is moderately spontaneous (– 60 kJ/mol) but largely endothermic (170 kJ/mol). The energetics (electornic and free) of the overall mechanism are presented in Figures 8 and 9 respectively. Kinetically, the rate determining step is found to be the bimolecular consecutive step. The geometrical variations of the transition states and intermediate during the course of reaction are as presented in Tables 9 and 10 below, while Tables 11 and 12 respectively show thermodynamic and kinetic parameters for the reaction.

Table 9: Variations in bond distances during transformation through TSI, INT and TSII benzalmethylketone and semicarbazide

TSI	Bond Length (A0)	INT	Bond Length (A0)	TSII	Bond Length (A0)
C9,O2	1.347	C10,O2	1.428	C8O2	2.318
O2,H1	1.368	O2,H19	O.970
C9,N1	1.666	C10,N1	1.478	C8N1	1.331
N1,H1	1.208
N1,H2	1.023	N1,H10	1.018	N1H2	1.073
N1,N2	1.410	N1,N2	1.405	N1,N2	1.410

 

Eventual break off of C-O bond in the final product was indicated as the bond length increases by 0.971   from the first transition state (TSI) to the second transition state (TSSII). However characteristic C=N bond formation [15] was shown as the bond length decreases progressively by 0.335  at TSII. Meanwhile, N1-N2 bond order was observed to remain unchanged being distant from active center. While C8C9C10 alternates by -1.27 ̊ at INT and by 7.84 ̊ at TSII, C8C9O2 decreases continuously by 9.46 ̊ at INT and by 15.25 ̊ at TSII.

Table 10: Variations in bond angles during transformation through TSI, INT and TSII benzyl methyl ketone and semicarbazide

TSI		INT		TSII
<C8C9C10	113.91 ̊	<C7C10C8	112.64 ̊	<C7C8C9	120.48 ̊
<C8C9O2	116.02 ̊	<C8C10O2	106.56 ̊	<C7C8O2	91.31 ̊
<C10C9O2	115.89 ̊	<C7C10O2	110.56 ̊
<N1C9O2	91.85 ̊	<N1C10O2	112.77 ̊
<C9N1N2	126.04 ̊	<C10N1N2	114.86 ̊	<C8N1N2	116.48 ̊
<C10C9N1	107.91 ̊	<C7C10N1	104.54 ̊	<C7C8N1	116.88 ̊
<C8C9N1	108.32 ̊	<C8C10N1	109.90 ̊	<C8C9N1	121.48 ̊

 

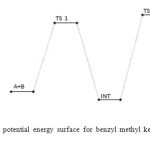Figure 8: Profiles of the potential energy surface for benzyl methyl ketone and semicarbazide reaction.  Click here to View figure

 

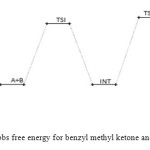Figure 9: Profiles of the Gibbs free energy for benzyl methyl ketone and semicarbazide reaction.  Click here to View figure

 

Table 11: DFT B3LYP (6-311+G**) Thermodynamic parameters for benzyl methyl ketone and semicarbazide reaction at 298.15 K

Species	ΔfH0(kJ mol-1)	S0(Jmol-1K-1)	G0(kJ mol-1)	Ee (kJ mol-1)
A	-106.21	370.73	-1113712.22	-1114057.47
B	-107.46	307.13	-736741.33	-736937.45
TSI	-223.17	464.72	-1850294.44	-1850833.46
INT	-262.40	455.77	-1850454.33	-1851011.73
TSII	-295.48	476.75	-1850278.96	-1850815.87
P1	+10.99	442.44	-1649784.07	-1650265.32
P2	-237.59	189.17	-200732.23	-200558.16

 

Table 12: DFT B3LYP (6-311+G**) Calculated kinetic parameters for benzyl methyl ketone and semicarbazide reaction at 298.15 K

Steps	A	k2               (dm3mol-1s-1)	K2	k1                         (s-1)	K1
A+B TSI	3.38 102dm3mol-1s-1		8.6369 10-4
A+B INT		2.1087 103
INTI TSII	2.11 1014 s-1				1.0508 10-4
INT P1+P2				4.8366 1019

 

The general reaction mechanism for reaction between 2-hexanone and semicarbazide is as presented in Figure 10 below.

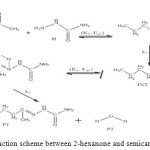Figure 10: General reaction scheme between 2-hexanone and semicarbazide.   Click here to View figure

 

The first activated complex (TS1) formation appears to be exothermic and non-spontaneous with a barrier height of (176 kJ/mol).  This step has equilibrium value for this step suggest that only very few reacting molecules actually pre-aggregate to form the activated complex, necessitating the need for reaction condition adjustment for forward equilibrium. The transition state proceeds to form the intermediate (INT) through O–H single bond formation, C–N single bond formation, C=O bond cleavage and N–H single bond cleavage, with their corresponding bond length and bond angle shown in the Table below. The intermediate has lower stabilization energy of (168 kJ/mol) than the activated complex TS1 as shown in Figure 12 below. The intermediate, by intra-molecular interaction through C=N and O–H bond formation leads to second activated complex TS II. This intra-molecular step is both exothermic by (–106 kJ/mol) and non-spontaneous by +62 kJ/mol, with some reasonable equilibrium value and energy height of 80 kJ/mol (Figure 11) [16].  Finally, through C–O bond cleavage and subsequent dehydration, the transition state (TSII) forms the products (semicarbazone and water). The two consecutive steps are competing for the reaction rate determination, but the bimolecular (first) step manage to be the rate determining step, since the higher the rate constant value the faster the reaction [17].

Table 13: Variations in bond distances during transformation through TSI, INT and TSII 2-hexanone

TSI	Bond Length (A0)	INT	Bond Length (A0)	TSII	Bond Length (A0)
O1,H3	1.378	O1,H11	0.963
C2,O1	1.345	C5,O1	1.456	C5,O1	2.362
C2,C3	1.545
C2,N1	1.671	C5,N1	1.461	C5,N1	1.327
N1,H3	1.201			N1,H8	1.064
				O1,H8	1.700

 

Table 14: Variations in bond distances during transformation through TSI, INT and TSII 2-hexanone

TSI		INT		TSII
<C2N1H3	72.22̊			<C5O1H8	53.10̊
<C2O1H3	79.14̊	<C5O1H11	108.39̊	<N1H8O1	112.42̊
<N1C2O1	92.13̊	<N1C5O1	112.01̊	<N1C5O1	71.98̊
<O1H3N1	115.48̊
		<C5N1H8	111.79̊	<C5N1H8	105.46̊
		<C6C5N1	109.58̊	<C6C5N1	121.06̊
		<C4C5N1	108.39̊	<C4C5N1	119.10̊

 

Figure 11: Profiles of the potential energy surface for 2-hexanone and semicarbazide reaction.  Click here to View figure

 

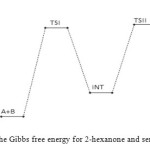Figure 12: Profiles of the Gibbs free energy for 2-hexanone and semicarbazide reaction.  Click here to View figure

 

Table 15: DFT B3LYP (6-311+G**) Thermodynamic and kinetic parameters for 2-hexanone and semicarbazide reaction

Species	ΔfH0 (kJ mol-1)	S0(Jmol-1K-1)	G0 (kJ mol-1)	Ee (kJ mol-1)
A	-276.81	359.37	-816674.47	-817033.12
B	-107.46	326.99	-736800.14	– 736937.72
TSI	-392.73	485.61	-1553244.62	-1553795.19
INT	-430.45	447.52	-1553412.39	– 1553982.12
TSII	-366.39	466.88	-1553236.48	– 1553786.52
P1	-170.35	435.90	-1352742.65	– 1353235.19
P2	-237.59	189.17	-200732.49	– 200558.16

 

Table 16: DFT B3LYP (6-311+G**) Calculated kinetic parameters for 2-hexanone and semicarbazide reaction at 298.15 K  Click here to View table

 

The general reaction mechanism for reaction between cinnamaldehyde and semicarbazide is as presented in Figure 13 below.

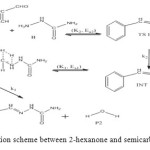Figure 13: General reaction scheme between 2-hexanone and semicarbazide.  Click here to View figure

 

The cinnamaldehyde and semicarbazide interact through C–N, O–H  bond formation and C–O bond cleavage to form TS1 with barrier height of about 21 kJ/mol compared to the starting molecules. The activated complex TSI is less stable than the two molecules A and B by (67 kJ/mol). This intermolecular engagement leads to intermediate with stabilization energy of 4 kJ/mol. The step (consecutive) leading to the intermediate formation is e-thermic and non-spontaneous with +71 kJ/mol free energy and very low equilibrium which suggests that input (in form of energy) is required to shift the reaction equilibrium forward. Again the intermediate undergoes intra-molecular interaction through C–N and O–H bond formation to form the second activated complex (TSII) which has an energy barrier of 58 kJ/mol but with appreciable equilibrium constant. The second transition state is highly unstable by 126 kJ/mol compared to the intermediate from which it was formed.  The second activated complex TSII eventually forms the major product and the leaving water molecules with high stabilization energy of (–216 kJ/mol). Free energy and potential energy reaction profiles (Figures 14 and 15) suggest a two-step mechanism involving two transition states and an intermediate, and the overall is slightly spontaneous by –19 kJ/mol and  exothermic by – 25 kJ/mol. The geometrical variations of the transition states and intermediate during the course of reaction are as presented in Tables 9 and 10 below, while Tables 11 and 12 respectively show thermodynamic and kinetic parameters for the reaction. The geometrical variations of the transition states and intermediate during the course of reaction are as presented in Tables 17 and 18 below, while Tables 19 and 20 respectively show thermodynamic and kinetic parameters for the reaction.

Table 17: Variations in bond distances during transformation through TSI, INT and TSII

TSI	Bond Length (A0)	INT	Bond Length (A0)	TSII	Bond Length (A0)
C8,C9	1.506	C8,C9	1.497	C8,C9	1.428
C9,O1	1.404	C9,O1	1.415	C9,O2	2.417
C9,N1	1.485	C9,N1	1.485	C9,N1	1.322
N1,H2	2.401			N1,H11	1.026
N1,N2	1.405	N1,N2	1.411	N1,N2	1.397
O1,H2	0.964	O1,H9	0.966	O2,H11	2.013

 

C8-C9 bond length decreases, while C9-O1 bond order increases progressively characteristic of bond fission in the final product. Again double bond order characteristic of C=N in the product was indicated by the continuous bond decrease from TSI through INT to TSII. Also worth mentioning is the O-H bond stretching by 1.049  preparatory to its cleavage in the final product. Similar variations were also observed in bond angles as the system undergoes transformation through TSI, INT and TSII to the final product.

Table 18: Variations in bond Angles during transformation through TSI, INT and TSII

TSI		INT		TSII
<C7C8C9	125.11 ̊	<C7C8C9	123.19	<C7C8C9	127.57
<C8C9O1	109.83 ̊	<C8C9O1	108.34	<C8C9O2	123.84
<N1C9O1	110.00 ̊	<N1C9O1	106.08	<N1C9O2	79.17
<C8C9N1	113.30	<C8C9N1	114. 53	<C8C9N1	130.14
<C9N1H2	53.70 ̊
<C9N1H10	109.70 ̊	<C9N1H11	108.71	<C9N1H11	111.52
<C10N2N1	120.13	<C10N2N1	118.14	<C10N2N1	120.53
		<C9N1N2	112.74	<C9N1N2	122.50

 

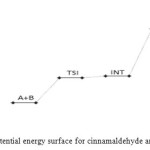Figure 14: Profiles of the potential energy surface for cinnamaldehyde and semicarbazide reaction.  Click here to View figure

 

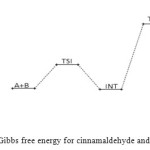Figure 15: Profiles of the Gibbs free energy for cinnamaldehyde and semicarbazide reaction.  Click here to View figure

 

Table 19: DFT B3LYP (6-311+G**) Thermodynamic and kinetic parameters for cinnamaldehyde and semicarbazide reaction

Species	ΔfH0(kJ mol-1)	S0(Jmol-1K-1)	G0 (kJ mol-1)	Ee (kJ mol-1)
A	+20.11	364.06	-1110542.45	-1110830.99
B	-107.46	326.99	-736799.88	-736937.45
TSI	-97.49	448.26	-1847275.64	-1847747.96
INT	-121.49	449.87	-1847271.44	-1847769.76
TSII	-143.60	455.99	-1847145.94	-1847711.47
P1	+114.47	435.43	-1646629.26	-1647051.71
P2	-237.59	188.86	-200732.49	-200741.95

 

Table 20: DFT B3LYP (6-311+G**) Calculated kinetic parameters for Cinnamaldehyde and semicarbazide reaction at 298.15 K

Steps	A	k2               (dm3mol-1s-1)	K2	k1 (s-1)	K1
A+B TSI	9.5441 dm3mol-1s-1		2.1710 10-14
A+B INT		7.7197 102
INTI TSII	3.5232 1013s-1				2.4582 109
INT P1+P2				9.6855 1016

 

Mechanism and Rate Law of the Reaction

Below are the elementary steps making the formation mechanism

 

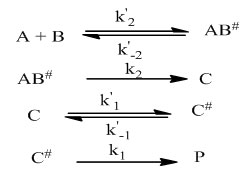
The rate laws for all the products of the reaction can be written as follow:

 

 

Conclusion

Formation mechanisms of five semicarbazones have been investigated at B3LYP (6-311+G**) theory level. The bimolecular consecutive was found to be the rate determining step except in the (Z)-2-(hexan-2-ylidene)hydrazinecarboxamide formation mechanism where both the bimolecular and unimolecular consecutive steps were found to be competing (k₂ = 2.40 10² dm³mol^-1s^-1 and k₂ = 3.81 10² s^-1), with the bimolecular still becoming the rate determining step and the unimolecular step the fastest. During the course of transformation through the first transition state (TS1), intermediate and second transition state (TS2) to the product geometrical (bond lengths and bond angles) variations alongside bond cleavage and bond formation were observed.

Authors’ contributions

AAS carried out the total experimental work under the guidance of UA. SD performed the data analysis, while HA prepared all the JPEG files, with AAS drafting the manuscript. All authors read and approved the final manuscript.

Acknowledgements

The authors are grateful to the head of the department of chemistry of Ahmadu Bello University for systemic support through the provision of dedicated power source.

Competing interests

The authors declare that they have no competing interests.

References

1. Liu, G., Cogan, O. A., Ellman, J. A.,  J. Amer. Chem. Soc. 1997, 119: 9913-9914
2. Kleinman, E. F., Chapter 4. In: Comprehensive Organic Synthesis, 3rd ed., Trost, B. M.; Fleming, I. (eds.), Pergamon Press, Oxford, 1991, Vol. 2, p. 893).
3. Blaser, H. U., Pugin, B., Spinder, F., Togni, A., Comp. Rend. Chim. 2002, 5: 379-385
4. Rudolph A. C., Machauer R., and Martin S. F., Tetrahedron Letters 2004; 45: 4895.
5. Pandeya, S. N., Mishra, V.;,Ponnilavarasan, I.;,Stables, J. P.,  Pol. J. Pharmacol., 2000, 52, 283.
6. Singh, H. P., Chauhan, C. S.,  Pandeya, S. N., Sharma C. S., Srivastava B. and Singhal M.,. Der. Pharm. Lett. 2010, 2: 460-462.
7. Singhal, M. and A. Paul, 2011b.. Global J. Pharmacol., 5 60-66.
8. Becke A. D.,  J. Chem. Phys. 1993, 98, 5648 (b) Lee C., Yang. W.,  Parr. R. G., Phys. Rev. B; Condens. Matter Mater. Phys. 1988. 3, 785.
9. Huang W., Jicun L., Xinli S., Yuzhen L., Hua H., Baoshan W., Hongmei S. and Fanao K. J. Phys. Chem. A 2006, 110, 10336 – 10344
10.  Gonzalez, C.; Schlegel, H. B. J. Phys. Chem.1969. 90,2154.
11.  Hideo, T., Hakuai, I., Masato M. I., J. Comput. Chem. Jpn., vol. 2, 4, pp. 127-134 (2003).
12.  Shabaan A. K. E., and Saadullah G. A., Chemistry Central Journal 2011, 5: 66
13.  Isamu S., Tadafumi U., Mitsuru S., Hideaki K., Hiroyuki O and Yujiro H.  Organic Letters 2006 vol.8, No.6, 1041-1044
14.  Hideo T., Hakuai I and Masato M. I. J. Comput. Chem. Jpn vol.2, No. 4 pp 127-134 (2003)
15.  G.S. Hammond. J. Am.chem. Soc. 77, 334 (1955)
16.  Robert C. M., Heidi M. M., and Peslherbe G. H., Can. J. Chem. 83; 1615-1625 (2005)
17. Szajewski R. P. and Whitesides G. M.  Journal of the American Chemical Society, vol. 102, No. 6, pp. 2011–2026, 1980.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.