Predicting ESR Peaks in Titanium (III), Vanadium (IV) and Copper (II) Complexes of Halo Ligands by NMR, ESR and NQR Techniques: A DFT Study

Introduction

We applied ADF 2010.02[1-10] to fifteen Ti (III), V (IV) and Cu (II)complexes with halo ligands. Each one of these three metal ions possessed only one unpaired electron. Cryoscopic conditions needed during ESR transitions of Ti (III) and V (IV) complexes[11-15]falling in low energy microwave region were difficult to obtain and cumbersome to maintain.No doubt, ESR spectra of Cu(II)complexes could be obtained at room temperature but the presence of  the large Jahn-Teller effect and the high l_Cu(II) [-830 cm^-1]  values would, again , cause errors[16-24]in their experimentally determined the A_ten parameters. All these difficulties were overcome by the ADF software.

DFT enabled us to deeply understand the relation between magnetic parameters and electronic and geometrical structures of molecules. As ESR was related to the electronic structure and geometry of systems, DFT provided an alternative to the traditional Hartree – Fock (HF) and post-HF approaches to the calculation of ESR parameters. This had   brought DFT on the forefront in calculating ESR parameters during the last decade.

The software gave one ESR [Hyperfine Coupling Constant (A _ten)], two NQR [Nuclear Quadrupole Coupling Constant(Q) , Asymmetric Coefficient (h)]  and two NMR  parameters[Shielding Constant (σ),Chemical Shift (δ)]  of  metal ions and Coordinating Atoms (CA).With the help of the 5 parameters: A _ten , NQCC,h, σ, δ ,we could predict the number of ESR peaks in  halo complexes of these three univalent metal ions.

A very brief back ground of the development of DFT as applied to NMR of complexes of transition metal ions was given as follows:

While the discussion on NMR of transition metal complexes encircled around ligand field theory [25], in the late 70s, some review articles were collected [26] on small molecules. De Brouchere (1978) published a 100 page review containing 289 references [27]. But till then no calculations on nuclear shielding and spin- spin coupling parameters were carried out. HFapproach given by Nakatsuzi [28]did present a paper on the calculation of the above named parameters of the complexes. But it was found lacking in high oxidation states of d¹⁰ systems [29].In 80s, NMR shielding codes based on HFSor X α method were developed which was latter known as DFT [29-31]. In 1993, Kohn-Sham DFT[32,33] employed IGLO method[32,33] to calculate nuclear shielding. LORG approach [34] as improved upon by GIAO*DFT [35-37] and CSGT methods[37] was employed. The spin-spin coupling constants (j) of the metal complexes were first of all calculated by Malkin et al[38].In 1996, Dickson and Zieglar [39] calculated FC term[40]by finite-perturbation approach. Later on, SD term[41,42] was also included in spin- spin coupling values.

The following 15 complexes such as [TiX₄]^1- (X=F, Cl, Br, I), [TiX₆]^3- (X=F, Cl, Br), [VF₄]⁰ (X=F, Cl, Br, I), [CuX₂]^2- (X=F, Cl , Br, I)  were studied.

With the help of the five parameters A _ten , NQCC,h, σ, δ  one ESR [Hyperfine Coupling Constant (A _ten)], two NQR [Nuclear Quadrupole Coupling Constant(Q) , Asymmetric Coefficient  (h)]  and two NMR  parameters[Shielding Constant (σ) ,Chemical Shift (δ)]  of  metal ions and  Coordinating Atoms (CA), we were able to predict the number of ESR peaks in the halo complexes of these three univalent metal ions [Ti (III), V (IV),Cu (II))].

Basis for prediction of the number of ESR peaks

As already stated, a total of 5 parameters of ESR (A _ten), NQR (NQCC,h) and NMR (σ, δ) of the metal ion and the coordinating atoms of ligands as obtained from the software were needed. The metal ion should have only one specific value for each one of these parameters, but these parameters might differ in values for coordinating atoms (CA) of the ligands. If the coordinating atoms had the same or nearly the same values of these five parameters, it would indicate that all the ligands were spatially equivalent. They might, further, undergo hyperfine interaction with the metal ion.  Both the hyperfine interaction and relative magnitude of the parameters for metal and CA will form the basis to determine the number of ESR peaks.

Prediction of Hyperfine Interaction between Metals and Ligands in Ti (III) and V (IV) Complexes

After knowing the values of nuclear quantum number and g factor of the nucleus of metal (I_M,  g _M) and of the coordinating atoms (CA) of ligands (I _CA , g _CA) from the literature, we would calculate the nuclear magnetic moments in terms of β_n  both for  the metal (μ_M)  and the coordinating atoms (μ_CA) of ligands as follows:

_μM =g _M [I_M (I_M+1)] ^1/2         |

And                         |   ——————————-   (a)

_μCA =g _CA [I_CA (I_CA+1)] ^1/2      |

Then [μ _M/μ _CA] ratio called μ_n ratio was calculated to draw the following inferences:

If this ratio was comparable and isotopes with non zero I possessed appreciable % natural abundance, the unpaired electron would be delocalized both on the metal ion and the ligands. So the hyperfine interaction between metal and ligands should be possible.

The peaks should arise both from the metal ion and the ligands.

Small or large ratios implied that μ_CA of ligands and the metal (μ_M) differ largely. No hyperfine interaction between metal ion and ligands should be possible. The electron would be localized only on metal ion irrespective of the values of I and % abundance of metal ions and CA.

The peaks should arise only from the metal ion.

Prediction of Hyperfine Interaction between Metals and Ligands in Cu (II) Complexes

The presence of a large Jahn-Teller effect, generally, allowed the hyperfine interaction and the peaks should arise both from the Cu (II) and the coordinating atoms of the ligands irrespective of their [μ_Cu /μ _CA] ratios.

Rules for calculating ESR Peaks in the metal ion Complexes  

 If I_M andI_CA were the nuclear spinsofmetal (M) and the CA respectively. Then:

(A)Number of ESR peaks given by a metal ion would be 2I_M +1 — (b)

(B)Peaks arising from ligands could be predicted from their stereochemical arrangement if the hyperfine interaction was possible as follows:

(i) When all the n ligands were spatially equivalent, then each ESR line of metal ion would split up into lines:

(2 n I_CA+1)—————————————————————–      (c)

(ii) If n₁ ligands were spatially of one type; n₂ of the other type and so on, then

total number of lines into which one line of the metal ion  split would be :

(2 n₁ I_CA+1)(2n₂ I_CA+1)(2 n₃ I_CA+1)———————————— (d)

(iii) If all the ligands were spatially nonequivalent, one line of metal ion would split into:

(2 I_CA+1) ⁿ —————————————————————- (e)

(c) In case, the A _ten of the metal ion was higher than that of CA, then first the lines obtained from metal ion should be calculated. Each one of this line could, further, split into a number of lines given by coordinating atoms if hyperfine interaction among the metal ion and the ligands was possible. Conversely, if coordinating atoms possessed higher A_ten value/s, then first the lines given by the ligands were calculated. Each line of ligands would, then, split by the metal ion.

(d) There could happen an overlapping of ESR lines due to different reasons. So, experimentally observed number of lines might be less than theoretically predicted lines. Further, if the predicted number of lines were very large with small A_ten values of species, the lines would merge to give a continuum.

Material and methods

Obtaining ESR and NQR parameters

After optimization of complexes, the software was run by Single Point, LDA, Default, Spin Orbit, Unrestricted,  Collinear commands using DZ or TPZ Basis sets with Nosym symmetry in its “ESR/EPR Program” to obtain ESR (A_ten) and NQR (NQCC,η) parameters for the Cu(II) and the coordinating atoms (¹⁴N, ³⁵Cl, ⁸⁹ Br, ¹²⁷ I)  of the ligands [43-46].

Obtaining NMR Parameters

σ and δ values of Cu (II) and ¹⁴N, ³⁵Cl, ⁸⁹ Br, ¹²⁷ I of ligands were obtained from “NMR/EPR Program” by the above commands except for replacing Spin Orbit by None [35, 9-10].

Results

Table: 1A gave expanded forms of acronyms. Tables: 1B contained I_M, I _CA, g_M, g_CA , μ_M and μ_CA (in terms of β_n) and ratios (μ_n) of μ_M and μ_CA to predict the possibility of hyperfine interaction between the metal ion and ligands.Tables:1C gave values of A _ten , NQCC,h, σ, δ  parameters  of CA of ligands, number of spatially different ligands along with A _ten ,σ, δ values of  the metal ions along with the number of theoretically expected ESR peaks.

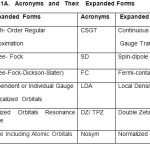Table1A: Acronyms and Their Expanded Forms.  Click here to View table

 

Discussion

Prediction of number of ESR peaks in Ti (III) Complexes

Table: 1B predicted of Hyperfine Interaction between Ti (III) and the halo ligands. Table: 1C contained A _ten ,  σ , δ values of the parameters  of Ti(III) and the A _ten , NQCC, η , σ , δ parameters of  halo ligands for [TiX4]^1- ( X= F, Cl, Br, I) along with the predicted  number of  ESR peaks.

Their ESR discussion was divided into two parts:

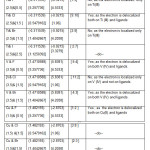Table1B: Prediction of Hyperfine Interaction between Metals and Ligands  Click here to View table

 

Prediction of ESR peaks in [Ti X₄]^1- (X =F, Br, I)

They showed the following common features:

[i] The four halo ligands possessed same values of A _ten , NQCC , η, σ , δ  parameters respectively to show that all the ligands were spatially equivalent. [ii] A _ten of Ti (III) was higher than those of the ligands. [iii] The unpaired electron was localized only on Ti (III) because the small μ_Ti / μ_CA ratio would not allow any hyperfine interaction.

Their ESR spectra would show only a large sextet from Ti (III) [2.5/2+1].

Prediction of ESR peaks in [TiCl₄]^1-

It showed the following features:

[i] Four chloro ligands possessed same values of A _ten, NQCC,h , σ, δ  parameters respectively.So all the ligands were spatially equivalent.[ii] A_ten of Ti (III) was higher than  all the chloro ligands. [iii] Ti (III) and ligands had comparable μ_Ti / μ_Cl ratio to allow unpaired electron to be delocalized. So the hyperfine interaction was possible among them.

Its ESR spectrum would give a large sextet from Ti (III) [2.5/2+1].Its each line would, further, split up into a tridecane from 4 equivalent Cl [2.4.3/2+1] due to hyperfine interaction.

Prediction of ESR peaks in six- coordinate complexes [Ti X₆]^3- (X =F, Cl, Br)                                              Again, two cases would arise:

Prediction of ESR peaks in [Ti X₆]^3- (X=F, Br)

They showed the following common features:

[i] Six halo ligands possessed nearly the same values of their A _ten, NQCC,η , σ, δ parameters respectively to indicate that they were spatially equivalent. [ii] A _ten of Ti (III)was higher than those of the ligands. [iii]With small μ_Ti / μ_CA ratios, the unpaired electron was localized only on Ti (III).

Their spectra would give only a large sextet from Ti (III)[2.5/2+1] with no hyperfine interaction.

Table1C. Prediction of Number of ESR peaks in Metal Ion Complexes  Click here to View table

 

Prediction of ESR peaks in [TiCl₆]^3-

It showed the following features:

[i] It gave two sets of values of A_ten, NQCC, η, σ, δ parameters to indicate two types of chloro ligands; each type containing three ligands. [ii] A _ten of Ti (III) was higher than those of the ligands. [iii]The unpaired electron was delocalized both on Ti (III) and the ligands due to their comparable μ_Ti/ μ _{C l} ratio.

Its spectrum would give a sextet from Ti (III) [2.5/2+1]. Each line of this sextet would, further, split into 100 lines^{(d )}  from two types of spatially different Cl [2.3.3/2+1]² due to hyperfine interaction. In fact, a continuum should be observed.

Prediction of number of ESR peaks in V (IV) Complexes

Table: 1B predicted of Hyperfine Interaction between V (IV) and the halo ligands. Table: 1C contained A _ten ,  σ , δ values of the parameters  of V(IV) and the A _ten , NQCC, η , σ , δ parameters of  halo ligands for [VX4] ( X= F, Cl, Br, I) along with the predicted  number of  ESR peaks Their ESR discussion was divided into  two parts:

Prediction of ESR peaks in [V X₄] (X= F, Br, I)

They showed the following common features:

[i] The four halo ligands possessed same values of their A _ten, NQCC, η , σ, δ parameters respectively; meaning thereby that all the ligands were spatially equivalent. [ii] A _ten of V (IV) was more than those of the ligands. [iii] With comparable μ_V / μ_CA ratios, the unpaired electron would be delocalized both on the V (IV) and the ligands.

Their ESR spectra would first give a large octet from V (IV) [2.1.7/2+1]. Each line of this octet would, further, split up into a quintet or 13 lines or 21 lines from four equivalent F [(2.4.1/2+1)] or Br [(2.4.3/2+1)] or I [2.4.5/2+1)] respectively due to hyperfine interaction.

Prediction of ESR peaks in [V Cl₄]

It showed the following features:

[i] Four chloro ligands possessed same values of their A _ten, NQCC,η,σ, δ  parameters respectively; meaning there by that  the ligands were spatially equivalent.[ii]A _ten of V (IV)

was more than  those of the ligands.[iii] The unpaired electron was localized only on V (IV) and not on ligands as their μ_V / μ_Cl ratio was large.

So its ESR spectrum would give only a large octet from V (IV) [2.1.7/2+1] with no hyperfine interaction among the chloro ligands and V (IV).

Prediction of number of ESR peaks in Cu (II) Complexes

Table: 1B predicted of Hyperfine Interaction between Cu (II) and the halo ligands. Table: 1C contained A _ten ,  σ , δ values of  parameters  of Cu(II) and  A _ten , NQCC, η , σ , δ parameters of  halo ligands for [CuX4]^2- (X= F, Cl, Br, I) along with the predicted  number of  ESR peaks. Their ESR discussion was divided into  two parts:

Prediction of ESR peaks in [Cu X₄]^2- X= (F, Cl)

It showed the following common features:

[i] Both the ligands possessed  same values of their A _ten ,NQCC, η , σ, δ parameters respectively; meaning there by that they were spatially equivalent.[ii] A _ten of Cu (II)  was more than  ligands.[iii]Unpaired electron  was delocalized both on Cu (II) and ligands.

ESR spectra  should give a large quartet from Cu(II) [2.3/2+1] whose each line would, further, split up into a smaller  quintet or a tridecane from four equivalent F [(2.4.1/2+1)] or Cl [2.4.3/2+1] respectively due to hyperfine interaction  between Cu(II) and F or Cl.

Prediction of ESR peaks in [Cu X₄]^2- (X= Br, I)

They showed following common features:

[i] Both the ligands possessed same values of A _ten, NQCC , η, σ, δ parameters respectively; meaning there by that all were spatially equivalent. [ii] A _ten of Br and I were more than that of     Cu (II). [iii] The unpaired electron was delocalized both on Cu (II) and four equivalent ligands.

Their ESR spectra  would first give a large tridecane from the four equivalent Br [2.4.3/2+1] or 21 lines from four equivalents I [2.4.5/2+1].Then its each line would, further, split into a smaller quartet from  Cu (II) [2.1.3/2+1] due to hyperfine interaction between Cu (II) and Br or I.

Conclusion

The originality, the relevance, the objective of this work and how it moved the body of scientific knowledge forward would lay in the fact that we were able to theoretically predict the number of ESR peaks in Ti (III),V(IV) and Cu(II) complexes having mono-dentate ligands.

Acknowledgement

Authors gratefully acknowledge the kind and willing cooperation of Mr. Sunil Chawla [sunil@seascapelearning.com] of ADF (http://www.scm.com).They feel indebted to Mr. S.R. Heer, Chief Engineer (Retd.), North Zone, Doordarshan, New Delhi (India) for his invaluable cooperation in the installation and smooth working of the ADF software.

References

1. Mcgravey B. R. Electron spin resonance of transition metal complexes, Vol.III,; (1967), p.89-201.
2. Atanasov, M.; Daul, C. A. Comptes. Rendus.Chimie. 2005 8, 1421-33
3. Silichter, C.P. Principals of Magnetic Resonance, Sec.6.3.Harper and Row, N.Y.(1963).
4. Kaup, M.; Buhl, M.; Malkin, V.G. Calculation of NMR and EPR Parameters; Theory and Applications. Ed. Wieley-VCH-Weimheim (2004).
5. Lanthe, E. V.; Aroird, V.; Wormer, P.E.S. J. Chem. Phys. 1997107, 2488-98.
6. Lanthe, E. V.; Aroird, V.; Wormer, P.E.S. J. Chem. Phys. 1998 108, 783-96.
7. Lanthe, E. V.; Baerends, J. J. Chem. Phys. 2000 108, 8279- 92.
8. Lipkowitz K. B. and Boyd D. B. Kohn-Sham Density Functional Theory: Predicting and Understanding Chemistry, Vol. XV.  Wiley-VCH, New York, p.1-86.
9. Schreckenbach, G.; Ziegler, T. Int. J. Quantum Chem. 1997 61, 899.
10. Wolff, S. K.; Ziegler, T. J. Chem. Phys. 1998 109, 895.
11. Schoenherr, T.; Atanasov, M.; Schmidtke, H. H. Inorg. Chim. Acta. 1988 141, 27-32.
12. Benco, L.; Barras, J. L.; Atanasov, M.; Daul, C.; Deiss, E. J. Solid State Chem. 1999 145, 503.
13. Fona, S.; Low, W. Phys. Rev. 1960 120, 1585.
14. Saladino, C. A.; Larsen, C. S. Catalysis Today. 2005 1, 22-33.
15. Atanasov, M.; Daul, C. A.; Rauzy, C. Chem. Phys. Lett. 2003 367, 737-46.
16. Atanasov, M.; Daul, C. A.; Güdel, H. U.; Wesolowski, T.; Zbiri, M. Inorg. Chem. 2005 44, 2954-63.
17. Atanasov, M.; Nikolov, G. S. Proc. 10th Conference, CSSR. 1985, 11-16.
18. Nikolov, G.S.; Atanasov, M. Inorg.Chim.Acta. 1983 72, 95-101.
19. Atanasov, M.; Nikolov, G. S. Chem. Bulg. Acad. Sci. 1983 16, 329-36..
20. Atanasov, M. PhD Thesis. Bulgarian Academy of Sciences, Sofia, Bulgaria (1983).
21. Kutoglu, A.; Allmann, R.; Folgado, J. V.; Atanasov, M.; Reinen, D. Z. Naturforsch. 1991 46b, 1193-99.
22. Smith, A. S. Advances in Nuclear Quadrupole Resonance. Hayden and Sons, London, Vol. I (1974), Vol. II (1975), Vol. III (1977).
23. Reinen, D.; Atanasov, M.; Nikolov, G. S.; Steffens, F. Inorg.Chem. 1988 27, 1678 -86.
24. Atanasov, M.; Kesper, U.; Ramakrishna, B. L.; Reinen, D. J. Solid St.Chem. 1993 105, 1-18.
25. Ballhausen, C. J. Molecular Electronic Structures of Transition Metal Complexes.   Mc Gray -Hill, London (1979).
26. P. Pyykko (2004)“Theory of NMR parameters from Ramsey to Relativity, 1953 to 1983- in Calculation of NMR and EPR parameters -Theory and Applications”.p.7-19 Wiley-VCH, Weinheim
27. Brouchere, G. D. Adv. Chem. Phys. 1978 37, 203-304.
28. Tossel Kluwer, J. A.; Dordrecht Edited. Nuclear Magnetic Shielding and Molecular Structure (1993).
29. Bieger, W.; Seifert, G.; Eschrig, H.; Grossmann, G. Chem. Phys. Lett. 1985 115, 275-280.
30. Freier, D.G.; Fenske, R. F.; Xiao-Zheng. J .Chem. Phys. 1985 83, 3526-37.
31. Malkin, V. G.; Zhidomirov, G. M. Zh. Strukt. Kim. 1988 29, 32-36.
32. V.G.Malkin,O.L.Malkina,D.R.Salahub(1993)“Calculation of NMR shielding constants beyond uncoupled Density Functional Theory. IGLO approach”.Chem.Phys.Lett.204:87-95
33. V.G.Malkin,V.G.,O.L. Malkina .,D.R.  Salahub (1993) “Calculation of NMR shielding constants beyond uncoupled Density Functional Theory”.  Chem. Phys.  Lett.204: 80-86
34. Arduengo, A. J.; Dixon, D. A.; Kumashero, K. K.; Lee, C.; Power, W. P.; Zilm, K. W. J. Am. Chem. Soc. 1994 116, 6361-67.
35. Schreckenbach, G.; Ziegler, T. J. Phys. Chem. 1995 99, 606-10.
36. Rauhut, G.; Puyear, S.; Wolinski, K.; Pilay, P.  J. Phys. Chem. 1996 100, 6310-16.
37. Cheeseman, J. R.; Trucks, J. W.; Keith, T. A.; and Frisch, M. Chem. Phys. 1996 104, 5497-5509.
38. Malkin, V. G.; Malkina, O. L.; Salahub, D. R. Chem. Phys. Lett. 1994 221, 91-99.
39. Dixon, R. M.; Zieglar, T. J. Phys. Chem. 1996 100, 5286-90.
40. Autschbach, J.; Zieglar, T. J. Chem. Phys. 2000 113, 936-47.
41. Helgaker, T.; Watson, M.; Handy, N. C. J. Chem. Phys. 2000 113, 9402-09.
42. Sychrovsky, V.; Grafenstein, J.; Cremer, D. J. Chem. Phys. 2000 113, 3530-47.
43. Pederson, M. R.; Khanna, S.N.  Phys. Rev. 1999 60, 9566.
44. Neese, F. Chem. Phys. 2007 127, 164112.
45. VanWullen, C. J. Chem. Phys. 2009 130, 194109.
46. Schmitt, S.; Jost, P.; VanWullen, C.  J. Chem. Phys. 2011 134, 194113.

 

---

This work is licensed under a Creative Commons Attribution 4.0 International License.