High-Pressure Structural Phase Transition in Neptunium Compounds

Introduction

The high pressure structural phase transitions in rare earth compounds have been extensively studied both experimentally and theoretically in the recent past [1, 2]. At ambient pressure, it has been found that neptunium monochalcogenides i.e. NpSe and NpTe present interesting aspects among actinides monochalcogenides and have weak anti-ferromagnetism with an ordered magnetic moment of 2.5 μ_B and 2 μ_B respectively [3,4]. NpSe behaves as an insulator even at the highest pressure achieved (25 GPa) with relatively high resistivity values in the magnetic domain at low temperature and as semimetal in the non magnetic state. The delocalization of the 5f electrons leads to a reduction of the magnetic state [1]. NpTe behaves as insulator in NaCl structure and then a metallic shape in the CsCl structure. Thus, at the phase transition, insulator behaviour replaces metallic behaviour with a large decrease of resistivity in case of NpTe [5].The specific heat measurements confirms antiferromagnetic order in NpSe and NpTe below 36.5 and 45 K, respectively. The estimated magnetic entropy in NpS and NpSe is indicating the delocalized character of the Np 5f states [6]. All these properties of NpSe and NpTe motivate us to investigate the transition pressures, volume collapses and elastic behaviour of these compounds.

In present work, we have employed the two body potential model in which we have considered the realistic approach to analyze the phase transition and elastic properties in the NpSe and NpTe compounds. The model potential used in the present study is Born-Mayer type and the methodology is similar to our previous work [2].This is the classical and simple approach except the two parameters i.e.  hardness and range parameters are calculated separately for both the phases to make the results physically realistic.

Methodology

The Born-Mayer potential model consists of three terms and is expressed as

 

The first term is the Coulomb interaction energy and given as

Here  is Madelung constant and depends on the structure and Ze is the total ionic charge.

Second and third terms of eq. 1 are the nearest and the next nearest neighbor interaction energies and given by

and

Here N is the number of nearest-neighbor atoms, N′ is the number of next nearest-neighbor atoms, R is the nearest neighbor separation, r_N is  next-nearest neighbor separation, b  is  range  parameter and  is the  hardness  parameter.

The stability of a particular structure is decided by the minima of the Gibbs energy which is given by

G  = U +  PV –  TS                                                                    (5)

where , U is the internal energy at T=0 K and  is equivalent to the cohesive energy and S is the vibration entropy at absolute temperature T, pressure P and volume V. At T = 0 K and pressure P, the Gibbs free energy for NaCl (B1) and CsCl (B2) phases is expressed as

G_B1(r) = U_B1(r) + PV_B1                                 (6)

G_B2(r) = U_B2(r) + PV_B2                                 (7)

with V_B1 = 2r³ and V_B2 = 8/3∫3^r13 as the unit cell volumes for B1 and B2 phases respectively .Where r and r’ are the nearest neighbor separation for B1 and B2 phases.

Here U_B1 and U_B2 are the cohesive energies for B1 and B2 phases respectively and within the frame-work of the Born-Mater-type potential, U_B1 and U_B2 are expressed as

 

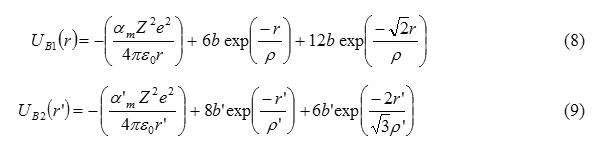
Here,a_m = 1.747565 and a¹_m = 1.762675 are the Madelung constants for B1 and B2 phases, respectively. p,b and p’,b’ are the hardness and range parameters for B1 & B2 phases respectively.

The phase transition pressure is the pressure at which the difference of Gibbs free energy of two phases becomes zero i.e

ΔG = GB₂(r’)- G_B1(r)=0                                  (10)

 

Value of p,b  for B1 phase can be determined from bulk modulus and the equilibrium condition. The equilibrium condition for B1 phase is given by [2]

From eq. (10) and (13), the value of b is

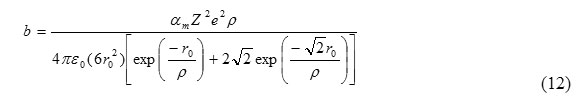
The thermodynamic condition for bulk modulus for B1 phase may be given as [2]

From eq. (10) and (15), we get

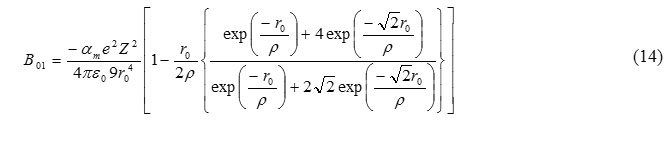
For B2 phase, range parameter can be calculated by the relation [7]

where 8 & 6 are the coordination numbers of B2 and B1 phases respectively. The value of hardness parameter p’ in B2 phase has been calculated from the minima of Gibbs free energy in B2 phase.

The equilibrium condition and bulk modulus for B2 phase can be given as

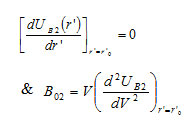
respectively. The Bulk modulus for B1 phase which describes the material’s response to uniform pressure, may be calculated from the relation

 

Results and Discussions

In order to calculate the phase transition pressure and elastic properties of NpSe and NpTe binary solids, we have used potential model approach. For B1 and B2 phases, the potentials are represented by equations (8) and (9) respectively. The input parameters such as equilibrium separation (r₀), bulk modulus (B₀) and the volume collapse at the transition pressure, which are required to calculate the potential or model parameters, are tabulated in Table 1 with their corresponding references. The calculated values of the model parameters are given in Table 2. Using these potential parameters the Gibbs free energies for B1 and B2 phases are calculated by using the Eqs. (6) and (7) at different values of pressure, whereas the inter-ionic separation for different values of pressure are calculated by minimizing the Gibbs free energy as the stability of particular crystal structure is given by minima of Gibbs free energy. Figs. 1 (a) and 2 (a) shows the variations of difference of Gibbs free energy (∆G) with pressure for NpSe and NpTe respectively. From these Figs. it is found that NpSe and NpTe undergo a phase transition from B1 to B2 at a transition pressure of 22.5 GPa and 16.0 GPa respectively.

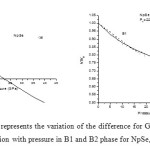Figure 1: (a) and (b) represents the variation of the difference for Gibbs free energies  (∆G) and volume compression with pressure in B1 and B2 phase for NpSe, respectively.  Click here to View figure

 

Figs. 1 (b) and 2 (b) present the pressure-volume relation for these Np compounds. It is observed that P-V curve is not a continuous curve. The first order phase transition involving a discontinuity in volume takes place at phase transition pressure. This discontinuity is known as volume collapse. At ambient pressure both of these compounds exist in NaCl–type structure (B1) and exhibit first order structural phase transition under high pressure. It is found from compression curves that NpSe and NpTe undergo a phase transition from B1 to B2 % volume collapse of 10.9 and 16.2 respectively. This volume collapse at the transition pressure is similar to the experimental observations [8, 9] as well as theoretical observation [10, 11] for NpSe and NpTe compounds and indicates that the increase in pressure favours a more compact structure. This larger volume change of these monochalcogenides at the transition pressure is due to the delocalization of their 5f electrons in the half filled 5f orbitals. This delocalized 5f electrons oppose the repulsive force between two ions and helps in the larger volume collapse at the transition.

The calculated values of phase transition pressure and cohesive energies for NpSe and NpTe in B1 and B2 phases are reported in Table 3. It is evident that the cohesive energy for B1 phase is greater than that of B2 phase. This shows that under ambient conditions NaCl type structure is more stable.

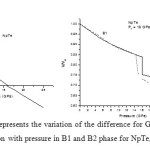Figure 2: (a) and (b) represents the variation of the difference for Gibbs free energies  (∆G) and volume compression with pressure in B1 and B2 phase for NpTe, respectively.  Click here to View figure

 

It is interesting to note that the nearest neighbour separation increases at B1 to B2 transition. For NpSe and NpTe, this distance increase from 2.680616 Å to 2.837795 Å and 2.922955 Å  to 3.076749 Å for high pressure B2 phase. The greater value of nearest neighbour separation for B2 phase than the B1 phase may be explained by the mechanism of the B1 to B2 transition in which the increase in pressure causes the unfolding of the bonding between the ions. Although the nearest neighbour separation increases for the high pressure B2 phase, the volume of this phase always remains less than that of the low pressure B1 phase because the volume of B1 phase is 2(r)³ while that of B2 is 1.54 (r΄)³.Others high-pressure behaviour of these monochalcogenides such as elastic constant and bulk modulus for B1 and B2 phase has also been predicted and tabulated in Tables 4. Valuable information about the nature of forces in the B1 phase of binary compounds may be obtained from the study of the three elastic constants C₁₁, C₁₂, and C₄₄. In present work, we have determined these second order elastic constants by using the relations given in ref.[2] and reported in Table 4.

The calculated values of bulk modulus for NpSe and NpTe for B1 phase come out to be 58.7 GPa and 89.2 GPa and for B2 phase 75.4 GPa and 22.2 GPa respectively. We have compared the calculated bulk modulus for B1 phase with the experimental and others calculated results but because of lack of experimental results for B2 phase, we could not compare bulk modulus for B2 phase with the experimental results.

At last it is pertinent to mention here that to study the B1-B2 phase transition and elastic properties ab-inito calculations and some computer simulation programs like, WIEN2K are extensively being used. But the aim of the present study is to formulate the simple and straightforward potential model which determines the B1-B2 phase transition pressure, the equation of state (compression curve) and the elastic properties within the same accuracy as done by such rigorous calculations and computer codes and on the basis of overall description it may be concluded that the potential model and its application in the present study assuming the different values of hardness and range parameter for both B1 and B2 phase explains the structure stability, cohesive, phase transition and the elastic properties of NpSe and NpTe  solids satisfactorily.

Table 1: Input parameters used to calculate model parameters

Crystal	14râ‚€”> (Å)	14Bâ‚€”> (GPa)	% volume collapse at  transition
NpSe NpTe	2.902 [10] 3.009 [10]	60 [8] 62 [9]	9.0 [8] 7.0 [9]

 

Table 2: Calculated model parameters, range parameters ( b, b’) and hardness parameters (ρ, ρ’) for B1 & B2 phases.

Crystal	b (10-19J)	ρ(Å)	b’ (10-19J)	ρ΄( Å)
NpSe NpTe	666.1007 3173.257	0.46012 0.38313	888.1343 4231.009	0.42757 0.36336

 

Table 3: Calculated results of cohesive energies, volume collapse and phase transition properties of NpSe and  NpTe.

Crystal	Equilibrium separation (Å)		Cohesive energy (10-19 J)		Transition pressure (GPa)	Volume Collapse (%)
NpSe Present Exp. Others NpTe Present Exp Others	2.680616 – – 2.922955 – –	2.837795 – – 3.076749 – –	-37.51184 – – -37.06811 – –	-37.51171- –     -37.06804 – –	22.5 23.0[12] 22.4[10] 23.4[11] 16.0 12-20[12] 14.2[10] 12.9[11]	8.65 9.0[12] 9.0[10] – 10.2 7.0[12] 10.0[10] –

 

Table 4: Elastic constants for B1 phase and Bulk modulus for B1 and B2 phases for compounds NpSe and NpTe

Crystal	C11 (GPa)	C12 (GPa)	C44 (GPa)	B (GPa)	B’ (GPa)
NpSePresent Exp. NpTe Present Exp.	58.32272 – 155.4857         –	58.93385 – 56.08719 –	62.74308 – 45.04205 –	58.7 60.0[8,12] 89.2 62[12]	75.4 – 91.47  –

 

References

1. Griveau J. C., Rebizant J. and Lander G. H., Physica B, 2006, 378–380, 976.
2. Srivastava A. K., Kumari S. and Gupta B. R. K., Phase Transitions, 2010 83, 28
3. Mattenberger K, Vogt O, Rebizant J, Spirlet J. C., Bourdarot F., Burlet P., Rossat-Mignod J., Bouillet M. N., Blaise A. and Sanchez J. P., J. Magn. Magn. Mater. 1992, 104, 105, 106, 107, 43
4. Trinadh Ch. U.M., Rajagopalan M, Natrajan S, J. Alloys Comp.,1998, 274, 18
5. Griveau J. C., Wastin F. and Rebizant J, Acta Physica Polonica B, 2003 34(2), 1319
6. Javorsky P,  Sanchez J. P, Wastin F., Colineau E., Rebizant J., Mattenberger K. and Vogt O.,  J. Magn.  Magn. Mater. 2007, 310(2), 1781
7. Kholiya K and Gupta B. R. K., Physica B , 2007 387(1-2), 271.
8. Gensini M, Benedict U and Rebizant J, J. Alloys Comp.1993, 201, L19
9. Dabos S. S., Benedict U., Heathman S. and Spirlet j. C., J. Less-common Metals 1990 160, 35
10. Jha P. K., and Sanyal S. P.,  J. Phys. Chem. Solids 2003 64, 127
11. Jha P. K., Aynyas M. and Sanyal S. P.,  Ind. J. Pure App. Phys. 2004 42(2)
12. Benedict U, Dabos-Seignon S., Dancausse J. P., Gensini M., Gering E., Heathman  S.and Luo H., Staun Olsen J., Gerward L., Haire R. G.,  J. Alloys Comp.1992 181,  1.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.