Effect of temperature on thermal properties of Graphene

Introduction

Graphene is a two dimensional crystalline material and discovered in 2004. It has exceptional mechanical properties  investigated by the different researchers [1–6] during recent past years. It has been found that electronic structure of graphene depends on the strain produced at different temperatures in it. Graphene band structure can be changed by applying strains larger than 15% [7]. In addition to that it is noted that a compressed  monolayer of graphene with size 30×100 μm² is fastened with 0.7% strain approximately[8]. There are two widely used theoretical approaches  available to study the various mechanical properties. These theories are based on elastic continuum and the  interatomic potentials (EP) [4, 9, 10] such as the Brenner potential (REBO) [11, 12] and the LCBOPII potential [13].

Due to instability coupled with stretching modes, the graphene is expected to be strongly anharmonic. This coupling  plays an important role to prevent the cracking in crystal and stabilize the flat phase [14] as confirmed by atomistic simulations for graphene [15] at room temperature. This is well established that anharmonicity is of general importance in condensed matter in relation to structural phase transitions [16, 17, 18], soft modes in ferroelectrics [18], melting [19], and other related phenomena. Since the  anharmonicity in crystals is very weak, it   can be  explained within  the framework of quantum theory of perturbation [16, 20– 22]. However, this is not true for graphene which is a strongly anharmonic crystal. Therefore, the atomistic simulations offer the possibility to study anharmonic effects for a specific material without the need of perturbation theory. A very accurate description of thermodynamic properties of different allotropes of carbon including graphene [15, 23] is provided by the empirical bond order potential LCBOPII [24, 25, 26].

Many interatomic potentials have been used to calculate the thermal and bending modulus properties of graphene  at zero temperature [11,12, 13, 18]. In the present study we have applied for the first time, the potential free model to analyze the thermal expansion behavior of graphene with varying temperature from room temperature to higher temperature range. The mathematical formulation is described in section 2 and the results are discussed in section 3.

Mathematical Formulation

Considering the product of thermal expansion coefficient α = 1/V (dV/dT)_p and bulk modulus (KT) remains constant [27, 28] under the effect of temperature i.e.

On the basis of equation (1) Singh and Gupta [29] derived the equation of state to determine the values of  α_T  and V/V_0. These expressions are given below:

 

δ_T⁰  is the value of Anderson Gruneisen parameter (δ_T) and α₀ is the thermal expansion coefficient at T₀ , K₀ is the bulk modulus and k is the dimensionless thermoelastic parameter. The  derivations for them are not derived here as they are already given elsewhere [29]. The equation (4) known as the integral form of equation of state has been used to calculate the nature of volume thermal expansion in graphene as shown in fig.1.

fig1

 

 

Results and Discussions

In the present paper we have determined the value of volume thermal expansion (V/V₀), using the integral form of equation of state (Eq. 4) and the thermal expansion coefficient (TEC)of graphene from equation (2) with varying temperature from room temperature to 1000K. The calculated values are shown in table 2 along with the available experimental data. The input data used in the present work are given in table 1 with appropriate references. The results on thermal expansion and thermal expansion coefficient of graphene achieved in the present work are also shown in figures 1 and 2 and compared with the experimental values.  It is clear from figs. 1and 2 that the results achieved in the present study are in close agreement with the experimental data. The negative values of thermal expansion coefficient (TEC) of graphene are conformed with the temperature dependent Raman spectroscopy [26] and  in good agreement with those values obtained from QHA-GGA ab- initio study [25]. This confirms the validity of the equation of state used in the present investigation to analyze the thermal expansion behavior of grapheme at high temperature.

On the basis of overall descriptions it is emphasized  that a simple and straightforward method used in the present study is capable of explaining the temperature dependent properties of graphene successfully. The methodology adopted in the present work may be of current interest to those researchers engaged in the study of mechanical properties of nanomaterials and alike materials.

Table 1: Input data used in present work for Graphene at room temperature

a˳(Å)	α o (10-6K-1)	K 0(eV Å-2)	δ̊T
2.4595     [9]	-4.8±1.0   [9]	12.7     [9]	2.0    [30]

 

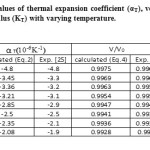Table 2: Calculated values of thermal expansion coefficient (αT), volume thermal expansion (V/V0) and bulk modulus (KT) with varying temperature.  Click here to View table

 

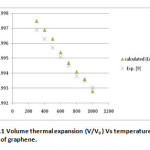Figure 1: Volume thermal expansion (V/V0 ) Vs temperature (T) of graphene.  Click here to View figure

 

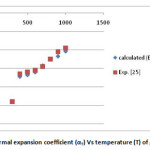Figure 2: Thermal expansion coefficient (αT) Vs temperature (T) of graphene.  Click here to View figure

 

References

1. Meyer, J.C.; Gein, A.K.; Katshelon, M.I.; Novoselov, K.S.; Booth, T.J.; Roth, S. Nature(London) 2007, 446, 60.
2. Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Science. 2008, 321, 385-388.
3. Booth, T.J.; Blake, P.; Nair, R.R.; Jiang, D.; Hill, E.W.; Bangert, U.; Bleloch, A.; Gass,M.I.; Navoselove, K.S.; Gein, A.K. Nano. Lett. 2008, 8, 2442.
4. Frank, O.; Tsoukleri, G.; Parthenios, J.; Papagelis, K.; Riaz, I.; Jalil, R.; Novoselov, K.S.; Galiotis, C. ACS-nano. 2010, 4, 3131.
5. Fasoline, A.; Los, J.H.; Katsnelson, M.I. Nature materials. 2007, 6, 858.
6. Bao, W.; Miao, F.; Chen, Z.;Zhang, H.; Jang, W.; Dames, C.; NingLau, C. Nat. nanotech. 2000, 4, 562.
7. Guinea, F.; Katsnelon, M.I.; Gein, A.K. Nat. Physics. 2009, 6, 30.
8. Tsoukleri, G.; Parthenios, J.; Papagelis, K.; Jalil, R.; Ferrari, A.C.; Gein, A.K.; Novoselove, K.S.; Galiotis, C. Small.2009, 5(21), 2397-402.
9. Zhakharchenko, K.V.; Katsnelon, M.I.; Fasoline, A.  Phys. Rev. Lett. 2009, 102, 046808.
10. Neck-Amal, M.; Peeters, F.M. Phys.Rev.B. 2010, 82, 085432.
11. Brenner, D.W. Phys.Rev. B. 1990, 42, 9458.
12. Brenner, D.W.; Shenderova, O.S.; Harrison,J.A.; Stuart,S.J.; Ni,B.; Sinnot,S.B. J.Phys. Condens. Matter. 2002, 14, 783.
13. Los, J.H.; Chiringhelli, L.M.; Meijer, E.J.;Fasoline, A. Phys. Rev. B. 2005, 72, 214102.
14. Piran, T.; Weinberg chapi. World Scientific. 2004, 6 and 11, Singapore.
15. Meyer, Jannik C.; Gein, A.K.; Katsnelson, M.I.; Novoselov, K.S.; Booth, T.J.; Roth, S. Nature(London). 2007, 446, 60.
16. Cowley, R.A. Adv. Phys. 1963, 12, 421.
17. Chen, Y.; Ho, K.M.;Harmon, B.N. Phys.Rev. B. 1988, 37, 283.
18. Souvatzis,P.; Erixsson,O.; Katsnelon,M.I.; Rudian,S.P. Phys. Rev. Let. 2008, 100, 095901.
19. Bratkovskii,A.M.;Vaks,V.G.;Trefilov,A.V. J.Exp.Theor.Phys.1984, 59, 1245.
20. Vaks, V.G.;Kravchuk,S.P.; Trefilov, A.V. J.Phys. F. 1980, 10, 2105.
21. Zoli, M. Phys. Rev. B. 1990,41,7497.
22. Katsnelson, M.I.; Trefilov, A.V.; Khlopkin, M.N.; Yu, K. Philos Mag.B. 2001, 81, 1893-1913.
23. Ghiringheli, L.M.; Los, J.H.; Meijer, E.J.; Fasoline,A.; Frenkel, D. Phys. Rev.Lett. 2005, 994, 145701.
24. Lifshitz, M. Zh.Eksp.Teor.Fiz. 1952, 22, 475.
25. Mounet, Nicolas; Marzari, Nicola. Phys. Rev. B. 2005, 71, 205214.
26. Yoou, Duhee;  Wooson, young; Cheong, Hyeonsik. Nano letters. 2011, 11, 3227.
27. Shanker, J.; Kumar,M. Phy.Stat. Sol. B. 1993,179, 351.
28. Anderson, O.L.; Zou, K. Phys.Chem. Mixer. 1989, 16, 642.
29. Singh, K.Y.; Gupta, B.R.K. Physica B. 2003, 334, 266.
30. Mohiuddin, T.M.G.; Lombardo, A.;  Nair, R.R.;  Bonnetti,  A.; Sarini, G.; Jalil, R.; Bonihi, N. ; Basko, D.M.; Ferrar,  A.C. Phys. Rev. B. 2009, 79, 205433.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.