Beads,Necklaces, Chains and Strings in Capping Carbonyl Clusters

Introduction

The Wade-Mingos rules have significantly enhanced the understanding and development of cluster chemistry since 1970s^1-2. Wade’s rule related the number of skeletal electron pairs(S_ep) in a cluster to the number of skeletal atoms(n) and hence a possible symmetry of the cluster was predicted. In order to fully appreciate the approach presented in this article, it is important to give highlights of Wade’s rule by illustrating its application with a few examples. Let us take B₆H₆^2― cluster with a regular octahedral symmetry³. If V represents the number of valence electrons of the cluster and B_e^H the number of electrons involved in the B-H bonds and S_e the skeletal electrons, then V = 3×6+6+2 = 26, B_e^H = 2×6 = 12 and hence S_e = 26-12 = 14. Therefore, the number of skeletal electron pairs in this case, S_ep = 14/2 = 7. Since n = 6 for B₆H₆^2― cluster, this give us the relationship S_ep = n+1 = 6+1. This is the same as,S_ep = n+1 which applies to all B_nH_n^2―closo clusters. In actual fact, this represents the closo series of clusters whose sleletal elements obey octet(8) or eighteen(18) electron rule.

Let us consider B₅H₉ cluster; n = 5, V = 3×5+9 = 24, ,B_e^H =2×5 =10, S_e = 24-10 = 14. Hence, S_ep = 14/2 = 7. In this example, S_ep = n+2 = 5+2 = 7. Thus, B₅H₉ (B-5)is a nido cluster a derivative of an octahedral cluster (B-6) where B-5 and B-6 represent the 5 and 6 skeletal elements respectively. The B-5 cluster will have an ideal square pyramid shape (C_4v)⁴ as opposed to B-6 octahedral shape(O_h). In addition to S_ep = n+2 relationship assisting us to predict the shape B₅H₉ cluster, it actually represents the nido series of clusters. Let us look at the last example of B₄H₁₀ cluster. In this case, n = 4, V = 3×4+10 = 22 and B_e^H = 2×4 =8. Therefore, S_e = 22-8 = 14 and S_ep = 14/2 =7. This gives us the series, S_ep = n+3 which represents arachno series and B₄H₁₀ cluster is a member. The geometrical relationship of arachno to that of the corresponding closo ‘parent’ may simply be represented as M-4→M-5→M-6. Hence, B₄H₁₀ is derived from B₆H₆^2―octahedral symmetry.On the other hand, Mingos related the series to the number of electron count of the cluster⁵. The relationship is as follows: (4n-2) Bicappedcloso, (4n) Monocappedcloso, (4n+2) closo, (4n+4) Nido, (4n+6) Arachno, and (4n+8) Hypho. Both Wade and Mingos relationship were derived from Molecular Orbital Theory⁶.

Results and Discussion

Universality of the 4n and 14n Rules

In an attempt to find a simpler way to teach Lewis shapes of simple molecules, a fundamental question arose.  Is there a simple formula that could link the number of atoms that obey the octet rule with the corresponding number of valence electrons? This was found and has been exceedingly useful in analyzing clusters such as hydrocarbons, boranes, heteroboranes and transition metal carbonyl clusters. Let us consider a few examples to illustrate how the cluster series were simply derived by this approach. Consider a C₂  diatomic molecule, n =2, the number of valence electrons for the two carbon atoms V =4×2 =8. But if the number of carbon atoms, n = 2 is multiplied by 4 gives the same numerical result as the total valence electrons, then S = 4×2 =  4n = 8 = V where S stands for series.  If  two hydrogen atoms (2H) are hypothetically added to the C₂ molecule, we generate C₂H₂ molecule.  This means that the two added hydrogen atoms have donated an additional 2 electrons giving rise to a total number of 10. If we take 4n as a standard or baseline on which other molecules with skeletal atoms that obey octet rule then C₂H₂, n =2, 4n =8, V =10. Therefore S = 4n+2 = V. Hence, C₂H₂ may be regarded as a member of S= 4n +2 series. How can we relate the number of bonds (k) in  the molecule to its series formula? We know that C₂H₂ has a triple (3) bond, and therefore  k = 2n-1 = 2×2-1 =3.  Thus, the two hydrogen atoms acted as ‘ligands’, guest or well-wisher atoms to simply donate the electrons to assist the ‘C₂’ skeletal atoms attain the octet rule. If we continue the process and add two more H atoms to the ‘C₂’ skeletal atoms we get C₂H₄,n =2, 4n = 8 and V=12. Hence S = 4n+4 and k = 2n-2 = 2×2-2 =2. This is in agreement with the double bond found in C₂H₄. If we use the same procedure for O₂ molecule, n = 2, 4n = 8, V =6×2 =12. Hence S =4n+4 and k =2n-2 = 2. That is, O₂ as in C₂H₄has a double bond although it does not need any donations from the well-wisher atoms.  Continuing adding the two hydrogen atoms we get C₂H₆. In this case, n =2, 4n = 8 and V= 14 and hence S =4n+6 and k = 2n-3 = 1. This means that C₂H₆ has one C-C bond.  On the other hand,the diatomic molecule F₂ gives us a similar result, n=2, 4n =8 and V= 14 and therefore S = 4n +6, and k =2n-3 = 1 without the support from donor atoms. This agrees with the single bond observed for F₂.  The method can be extended to heteroatomic systems. For instance, NO⁺, n =2, 4n =8, V = 5+6-1 = 10. Hence, S = 4n+ 2, k = 2n-1 = 3, the bond order of NO⁺. We can apply the method to skeletal atoms greater than 2. For instance,C₄H₄ , n=4, 4n =16, V = 20, S = 4n+4, and k = 2n-2 = 2×4-2 = 6.  With the k value of 6 , we can sketch a number of isomers. Two of these are sketched as shown in Figure 1.

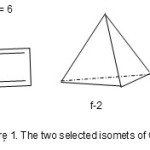Figure 1   Click here to View figure

 

The isomer f-1 has a planar shape but f-2 has tetrahedral symmetry, T_d. Also the As₄ molecule, n =4, 4n =16, V=20. Thus, S= 4n+4, and k = 2n-2 = 2×4-2 = 6. As₄ has a tetrahedral symmetry as in f-2.  Let us extend the method to M₄^4―  M = Si, Ge, Sn, Pb) ions⁷; n =4, 4n =16, V = 4×4+4 =20, S = 4n+4 and k =2n-2 =2×4-2 =6. These ions adopt a tetrahedral symmetry(T_d) as in f-2. Also the same tetrel elements form the M₅^2― (M =Si, Ge, Sn, Pb)ions; n =5,4n = 20, V =4×5+2 = 22, S = 4n+2, k =2×5-1= 9. This type of cluster system has been found to adopt a trigonalbipyramid (D_3h)⁷.Take a hydrocarbon, C₆H₆, n = 6, 4n=24 and V= 30, S = 4n + 6, k =2n-3 = 2×6-3 = 9.  This gives us two of the known benzene isomers among others and these are sketched in Figure 2(f-3 and f-4).

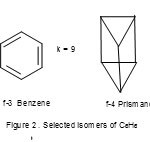Figure 2  Click here to View figure

 

Borane and Heteroborane Clusters

We could extend this approach to boranes and heteroboranes. Let us start with B₃H₈^― ion; n =3, 4n =12, V= 3×3+8+1 = 18, S = 4n+6 (Arachno), k = 2n-3 = 2×3-3 = 3. This means that the ideal shape of the B-3 skeletal atoms is a triangle⁸. A hydrocarbon, C₃H₆; n =3, 4n = 12, V = 18 has a k value of 3 and one of its isomers is a triangle. Let us follow up with B₅H₉ example; n =5, 4n =20, V = 3×5+9 = 24, S = 4n+4 (Nido), k = 2n-2 = 2×5-2 = 8. This is expected to have an ideal shape of a square pyramid (C_4v) as derived from Wade-Mingos rules^1-2. Let apply the method to the boron hydride ion B₅H₅^2―; n =5, 4n =20, V = 3×5+5+2 = 22, S = 4n+2, k = 2n-1 = 2×5-1=9. This is expected to have a shape identical to that of M₅^2― (M = Si, Ge, Sn, Pb) ions which is a trigonalbipyramid (D_3h).The  closoborane series is given by a general formula B_nH_n^2―(n = 2, 3, 4, 5, 6, 7, 8,9,10, 11, 12,..). The commonly encountered are from n =5→12. They belong to the cluster series S = 4n+2 and k = 2n-1. Hence the characteristic k-value for selected cluster are given  in Table 1. The generating functions of selected borane series are given in Table2.

Table 1: Characteristic k values of Selected Closo Boranes

Cluster	n	k = 2n-1
B2H22―	2	3
B3H32―	3	5
B4H42―	4	7
B5H52―	5	9
B6H62―	6	11
B7H72―	7	13
B8H82―	8	15
B9H92―	9	17
B10H102―	10	19
B11H112―	11	21
B12H122―	12	23

 

Table 2: Generating Functions of Borane Series

	Tetracp	Tricp	Bicp		Monocp	Closo	Nido	Arachno	Hypho
S =	4n-6	4n-4	4n-2		4n	4n+2	4n+4	4n+6	4n+8
F =	n-6	n-4	n-2		n+0	n+2	n+4	n+6	n+8
				1	BH	BH3	BH5	BH7	BH9
			B2	2	B2H2	B2H4	B2H6	B2H8	B2H10
			B3H	3	B3H3	B3H5	B3H7	B3H9	B3H11
		B4	B4H2	4	B4H4	B4H6	B4H8	B4H10	B4H12
		B5H	B5H3	5	B5H5	B5H7	B5H9	B5H11	B5H13
	B6	B6H2	B6H4	6	B6H6	B6H8	B6H10	B6H12	B6H14
	B7H	B7H3	B7H5	7	B7H7	B7H9	B7H11	B7H13	B7H15
	B8H2	B8H4	B8H6	8	B8H8	B8H10	B8H12	B8H14	B8H16
	B9H3	B9H5	B9H7	9	B9H9	B9H11	B9H13	B9H15	B9H17
	B10H4	B10H6	B10H8	10	B10H10	B10H12	B10H14	B10H16	B10H18
	B11H5	B11H7	B11H9	11	B11H11	B11H13	B11H15	B11H17	B11H19
	B12H6	B12H8	B12H10	12	B12H12	B12H14	B12H16	B12H18	B12H20

 

A closer analysis of Table 2 shows a very clear relationship of the well cited Rudolph relationship of borane and carborane shapes⁴. If Table 2 were to be expanded, it would be visible that important Rudolph geometrical relationship is a portion of the borane capping series. Let me present some of these series including those that were presented by Rudolph’s work by the structural formulas as seen in Table 2. Starting with B₁₂H₁₄(B₁₂H₁₂^2-)→B₁₁H₁₅→B₁₀H₁₆→B₉H₁₇. Then from B₁₁H₁₃→B₁₀H₁₄→B₉H₁₅→B₈H₁₆ at the end in the table. Final example is starting with the octahedral borane B₆H₈(B₆H₆^2-)→B₅H₉ (square pyramid)→B₄H₁₀→B₃H₁₁ at the end as indicated in the table.If the Rudolph capping series were to be extended, then the next starting cluster for de-capping would be B₁₃H₁₅, the next starting point would be B₁₄H₁₆, the next B₁₅H₁₇ and so on. It should be pointed out that no neutral closoboranes are known except that they occur as di-ionic B_nH_n^2―.

Other Important Main Group Clusters

To test the easiness of applying the 4n rule, let us consider a few more examples⁹.  Take Ge₉^4― ion; n = 9, 4n = 36, V = 4×9+4 = 40, S = 4n+4(Nido). Since the M-9 cluster is a Nido, it is a derivative of an M-10 closostructure, that is similar to B₁₀H₁₀^2-.  It will have one atom missing. As for Ge₉^2― ion; n = 9, 4n = 36, V = 4×9+2 = 38, S = 4n+2(Closo). Also its k value will be 2n-1 = 2×9-1 = 17 as in B₁₀H₁₀^2- cluster. It is therefore expected to have a similar shape. The last similar example to consideris  TlSn₉^3― ion; n = 10, 4n = 40, V = 3+4×9+3 = 42, S = 4n+2(Closo), k = 2n-2 = 2×10-1 = 19. This cluster is expected to have a skeletal shape as in B₁₀H₁₀^2―(comprises of two staggered square pyramid units joined together)³.

Transition Metal Carbonyl Clusters

While analyzing transition metal clusters, to find the link between the number of skeletal elements (n) and the valence electrons(V), it was found that some clusters were such that n when multiplied by 14 gave a result that was numerically the same as V. That is, 14n = V.  This became a parallel to that of the main group element clusters 4n = V. Such clusters were mono-capped clusters¹⁰ such Os₇(CO)₂₁, n =7, 14n = 14×7=98, V =8×7+21×2 = 98, S = 14n, and Os₆(CO)₁₈; n = 6, 14n = 14×6 =84 and V =8×6+18×2 = 84. Using 14n as a BASE LINE, other clusters were ‘standardized’ or their series deduced. Let us apply this 14n rule  to deduce the series of other clusters. Consider Mn₂(CO)₁₀, n =2, 14n = 14×2 = 28, V = 7×2+10×2 = 34, S = 14n+ 6 = V, and k = 2n-3 = 2×2-1 = 1. This implies a single bond between the two Mn atoms which is the case¹¹. This corresponds to 4n+6 of the main group elements. This implies the skeletal elements of transition metal carbonyl clusters behave in the same manner as those in corresponding main group clusters. Indeed if 10n is removed from S= 14n+6 we will remain with S = 4n+6 of the main group elements. For instance, in the above example if we remove 10n = 10×2 = 20 valence electrons, we will remain with 14 electrons for two skeletal elements. In other words, Mn₂(CO)₁₀ cluster behaves as X₂ cluster where X  is a halogen such as F, Br, Cl or I since for X₂ , n =2, 4n =8, V= 14 ,S = 4n+6 and k = 2n-3 = 2×2-3 = 1. This means X₂ has a single bond as in Mn₂(CO)_10.Let us determine the cluster series¹² of Rh₂(η⁵-C₅H₅)₂(CO)₂; n = 2, 14n = 28, V = 9×2+5×2+2×2 = 32; S = 14n+ 4, k =2n-2 = 2×2-2 = 2. This implies the cluster has double bond linking up the two Rh atoms. Since S= 14n+4 =V = 32, if we subtract an equivalent of 10n = 10×2 =20, then we will have an equivalent of S = 4n+4 = V= 12. Clearly, this result is the same as that of O₂ (n = 2, 4n = 8, V =12 and S =4n+4, and k = 2n-2 = 2). Consider Mo₂(η⁵-C₅H₄Me)₂(CO)₄; n = 2, 14n = 28, V = 6×2+5×2+ 4×2 = 30, S = 14n+2, k = 2n-1 = 2×2-1 = 3. This corresponds to a triple bond. Again, if we remove 20 from the valence electrons we will remain with 10. This will be equivalent to the cluster such as N₂ or C₂H₂ discussed earlier and known to have triple bonds. The main group cluster series were derived on the assumption each skeletal element obeyed the octet(8) rule. This implies an s²p⁶ electron configuration. On the other hand the eighteen(18) electron rule assumes an s²p⁶d¹⁰. Thus, it appears as if by removing 10n electrons from the transition metal cluster we are subtracting a d¹⁰ from each metal converting it to a main group element(s²p⁶d¹⁰-d¹⁰ =  s²p⁶). This means that the transition metal carbonyl series run parallel to a corresponding one of the main group elements. Hence,(14n+2, 4n+2) represent Closo Series, (14n+4, 4n+4) Nido Series, (14n +6, 4n+6)Arachno Series, (14n+6, 4n+6) Hypho Series, (14n, 4n) Monocapped Series, (14n-2, 4n-2) Bicapped Series, (14n-4, 4n-4) Tricapped Series, (14n-6, 4n-6) Tetra capped Series and so on. Classification of transition metal carbonyls using the 14n rule has recently been published^13-14.

Construction of A Hypothetical Table of Carbonyl Clusters

After analyzing the structure of cluster carbonyl series, it was observed that the capping series vary by a change in k value of 3 from one cluster member to the next involving an Os(CO)₂(14n-2 series) fragment while in the non-capping (ordinary)series the variation in k value is 2 units from one cluster member to the next involving an Os(CO)₃(14n+0 series) carbonyl fragment. With this knowledge in mind, a hypothetical table of osmium clusters was constructed. This is given in Table 3. This table can be extended where possible as required. The table is quite fascinating indeed. In order to analyze the characteristics of clusters, an assumption was made that the clusters in this case was that all clusters will comprise of osmium and carbonyl(CO) ligands only. Since the CO ligand donates two electrons, the charged clusters and other ligands are converted into CO ligand equivalent in terms of donating electrons. For instance, Os₆(CO)₁₈^2― is taken as Os₆(CO)₁₉ for the purposes of this analysis.The columns represent the ordinary series in which the expansion involves Os(CO)₃(14n+0) fragment which does not influence the change in the type of series for instance, the 14n represent the members of Mono-capped series which include, Os₂(CO)₆, Os₃(CO)₉, Os₄(CO)₁₂, Os₅(CO)₁₅, Os₆(CO)₁₈, Os₇(CO)₂₁, Os₈(CO)₂₄, and Os₉(CO)₂₇. One interesting member is Os(CO)₃ the building block fragment for non-capping series. The rows represent the capping series since the building fragment Os(CO)₂(14n-2) is a capping fragment containing the change “operator unit of (-2)”while the columns represent the ordinary series such as Hypho (14n+8), Arachno(14n+6), Nido(14n+4), Closo(14n+2), Monocap(14n), Bicap(14n-2), Tricap(14n-4), Tetracap(14n-6) and so on. Let us take the following capping series as seen in Table 3, namely¹⁰ ,

Os₂(CO)₁₀→Os₃(CO)₁₂→Os₄(CO)₁₄→Os₅(CO)₁₆→Os₆(CO)₁₈.The respective k values are given by (k = 2n-4 = 0, n =2), ( k = 2n-3= 3, n =3), (k = 2n-2  = 6, n =4), ( k = 2n-1, n =5) and ( k = 2n, n =6) which as a set are(0, 3, 6, 9,). This involves in change of k units by 3.  The value of k = 0 means that the clusterOs₂(CO)₁₀ exists as Os(CO)₅ molecules. The other k values imply the clusters have shapes changing from a triangle (k =3), to a tetrahedral ( k =6), to  a trigonalbipyramid ( k= 9) and to a capped trigonalbipyramid (k = 9+ 3 =12). These changes are shown in Figure 3.

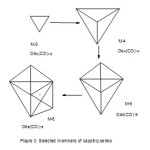Figure 3  Click here to View figure

 

However the change in k value from Os₅(CO)₁₆ ( k = 9) to Os₆(CO)₁₉  ( k = 11)  involves only 2 k-value units and the clusters belong to the same closo family and the shape goes from a trigonalbipyramid (D_3h) to octahedral(O_h).

Table 3: Generating Hypothetical Capping Osmium Carbonyl Clusters Click here to View table

 

Just as the elements of the periodic table have their atomic numbers and principal quantum numbers start with a digit of 1 and faithfully increase step by step with a numerical value of 1, the carbonyl clusters as derived from Table 3 have three main types of series namely, the ‘STRIPPING’series (Diagonal in Table 3) which lose 1 CO ligand step by step and have a cluster k value also correspondingly change by 1, the ‘CAPPING’ series (Horizontal or row in Table 3) with a periodic change of k value by 3 and the ‘ORDINARY’ series (Vertical or Column in Table 3) which vary with a periodic k value of 2.

Correlation Between 14 n Series of Transition Metal Carbonyl Series and 4 n Series of the Main Group Elements

When the corresponding series are compared, the correlation between the two series becomes vivid. This is illustrated in the Table 4 for a few selected series.

Table 4: Correlation Between Series of Transition Metal Carbonyls and Main Group Clusters

	KLAPO	HYPHO	ARACHNO	NIDO	CLOSO	MONOCP	BICP	TRICP	TETRACP
TM	14n+10	14n+8	14n+6	14n+4	14n+2	14n+0	14n-2	14n-4	14n-6	14n-8	14n-10
MG	4n+10	14n+8	14n+6	14n+4	14n+2	4n+0	4n-2	4n-4	4n-6	4n-8	4n-10
DIF	10n	10n	10n	10n	10n	10n	10n	10n	10n	10n	10n
TM = TRANSITION METALS, MG = MAIN GROUP, DIF = DIFFERENCE

 

Table 5:  Example Comparing Electron Counts for Closo Systems

CLOSO SYSTEMS, S = 14n+2 (TM), F(n) = 3n+1, MG, S = 4n+2, F(n) = n+2, M= Transition metal
TM	[M-1]	[M-2]	[M-3]	[M-4]	[M-5]	[M-6]	[M-7]	[M-8]	[M-9]	[M-10]	[M-11]	[M-12]
V	16	30	44	58	72	86	100	114	128	142	156	170
MG	BH2―	B2H22―	B3H32―	B4H42―	B5H52―	B6H62―	B7H72―	B8H82―	B9H92―	B10H102―	B11H112―	B12H122―
V	6	10	14	18	22	26	30	34	38	42	46	50
DIF	10	20	30	40	50	60	70	80	90	100	110	120
V = VALENCE ELECTRONS

 

Using generating functions, we can identify the closoosmium carbonyl systems that have the corresponding valence electrons.The generating function for closo series (S = 14n+2) is F(n) →(3n+1). Hence, the osmium closo carbonyl clusters are, [M-1] = 3(1)+1 = 4→Os(CO)₄, [M-2] = 3(2)+1 = 7→Os₂(CO)₇, [M-3] =3(3)+1 = 10→Os₃(CO)₁₀, [M-4] =3(4)+1 = 13→Os₄(CO)₁₃, [M-5] = 3(5)+1 = 16→Os₅(CO)₁₆, [M-6] = 3(6)+1 = 19→Os₆(CO)₁₉, [M-7] =3(7)+1 = 22→ Os₇(CO)₂₂, [M-8] = 3(8)+1 = 25→Os₈(CO)₂₅, [M-9] = 3(9)+1 = 28→Os₉(CO)₂₈, [M-10] =3(10)+1 = 31→Os₁₀(CO)₃₁, [M-11] =3(11)+1 = 34→Os₁₁(CO)₃₄, and [M-12] = 3(12)+1 = 37→Os₁₂(CO)₃₇. These closo osmium clusters are loaded with equivalent corresponding valence electron content. For example, [M-5] =Os₅(CO)₁₆ cluster has the valence electrons equivalent = 5×8+16×2 =72. Therefore, if we remove the “shielding” electrons(10n) from [M-n] system will produce an equivalent [B_nH_n]^2-closo system. In this example, [M-5]-50 = 72-50  =22 = [B₅H₅]^2-. Also an analysis of the series indicates that there is a close relationship between the series S =(14n+│q│) │and S‛ = (4n+│q│). That is, (14n+│q│) │- 10n = (4n+│q│). This implies that if we strip off the “shielding” electrons from transition metal elements in carbonyl clusters, we will find that they will behave like the corresponding main group elements. This is illustrated in Table 6.

Table 6: Correlation Between Transition Metal Carbonyl series and Main Group Series

	CLOSO SYSTEMS
14n+2	Valence electrons, TM	― 10n	Valence electrons, MG	4n+2
Carbonyl cluster				Possible main group equivalent
Os(CO)4	16	-10	6	BH2―
Os2(CO)7	30	-20	10	N2, C2H2
Os3(CO)10	44	-30	14	B3H11, C3H2
Os4(CO)13	58	-40	18	B4H6, C4H2
Os5(CO)16	72	-50	22	B5H52-, C5H2
Os6(CO)19	72	-60	26	B6H62-, C6H2

Os6(CO)182-	72	-60	26	B6H62-
Os7(CO)22	100	-70	30	B7H72-
Os8(CO)25	114	-80	34	B8H82-
Os9(CO)28	128	-90	38	B9H92-
Os10(CO)31	142	-100	42	B10H102-
Os11(CO)34	156	-110	46	B11H112-
Os12(CO)37	170	-120	50	B12H122-
M2(CO)8, M = Co, Rh, Ir	34	-20	14	X2, X = F, Cl, Br, I, C2H6
M2[Cp(CO)]2	32	-20	12	O2, C2H4, B2H6
[(Cp)(CO)2M2]2	30	-20	10	N2, C2H2
M3(CO)12 M = Fe, Ru,Os	48	-30	18	C3H6, B3H8―
M4(CO)12	60	-40	20	P4, C4H4
Rh6(C)(CO)152―	90	-60	30	C6H6
Fe5(C)(CO)15	74	-50	24	B5H9, C5H4
Co8(C)(CO)182―	114	-80	34	B8H82―
Co9(P)(CO)212―	130	-90	40	B9H13
Co10(P)(CO)223―	142	-100	42	B10H102―
Co13(N)2 (CO)243―	178	-130	48	B13H136―, B13H19

 

On the basis of the relationship between 14n and 4n system, it is possible to suggest a possible formula of the corresponding main group compound.  We can also make a correlation with boranes in the case of capped carbonyl clusters. For instance, Os₁₀(CO)₂₆^2― is known to be a tetracapped {C⁴C[M-6]} cluster. Whereas the capping fragment was identified as Os(CO)₂ which is a member of 14n-2 series and with electron content of 12, the corresponding capping fragment in boranes may be taken as (+B, -H) equivalent to adding having a content of 2 electrons. The (+B, -H) may be represented as [B, -H] or [B(-)H] in which case for every capping a B atom is added to the cluster while the H atom is subtracted each time.The fragment[B, -H] may be regarded as (4n-2) series corresponding to Os(CO)₂(14n-2)fragment . If we take  Os₆(CO)₁₈^2― as Os₆(CO)₁₉ to correspond to B₆H₆^2―, then capping Os₆(CO)₁₉ four times (4) will generate F = Os₆(CO)₁₉ + 4Os(CO)₂ →Os₁₀(CO)₂₇. If we apply the same process on B₆H₆^2― = B₆H₈ we get F = B₆H₈ + 4[B(-)H] which produces B₁₀H₄ borane cluster. For B₁₀H₄, n= 10, 4n = 40 and V = 34 and hence, S = 4n-6 and C_p = C¹+C³ = C⁴C[B-6]. This implies the octahedral cluster of 6 boron atoms will, in theory, be capped with 4 B atoms. In the case of capping boranes, the process involves replacing every H atom in the neutral borane known or unknown by a B atom. This means for B₆H₆^2― = B₆H₈ we can, in theory, cap it 8 times resulting into a final B₁₄ cluster. It is fascinating to note that B_n(n = 3-15) boron clusters are being studied¹⁵.

Beads, Strings and Chains of Clusters

The way Table 3 is constructed is like chains or strings of cluster units(molecules) increasing as we move from left to right along the capping series. The clusters can be synthesized by adding atoms, fragments, and molecules to make small or short , medium or large clusters. It imitates the way beads are put together to make short or long necklaces. In a way, the process is like putting chains tother to make long ones or train cabs being assembled.  For instance the cluster chain may start with one skeletal atom (M-1) at one end goes up to more than 30 skeletal atoms(M-30) at the other. In principle, such chain could go on indefinitely by adding one skeletal atom at a time. Since moving from left to right involves the addition of Os(CO)₂(14n-2) fragment, we can generate horizontal capping cluster series starting with Os atom as follows: Os→Os₂(CO)₂→ Os₃(CO)₄→ Os₄(CO)₆ → Os₅(CO)₈ → Os₆(CO)₁₀  → Os₇(CO)₁₂ → Os₈(CO)₁₄ → Os₉(CO)₁₆ → Os₁₀(CO)₁₈ and so on. It has been shown in this illustration how a capping series can be created starting with Os (horizontal row). This is a simple example of one of the rows of the capping series and Os(CO)₂(14n-2) fragment may be regarded as a capping constant.The same applies to the movement from the top to bottom for an ordinary cluster series such as closo or nido. The series are mathematically precise in terms of the content of valence electrons. For instance the table classifies osmium atom (Os) (see beginning of the Table 3)as a member of 14n-6 (tetracap)series thus, Os→ Os₂(CO)₃ → Os₃(CO)₆. The corresponding valence electron contentare numerically equal to 8, 22, and 36. This sequence varies by 14 electron units as expected from ordinary carbonyl series. The osmium atom also obeys the series S =14n-6 =V as n = 1 for one osmium skeletal ton S = 14(1)-6 = 8 the valence content of osmium. If we continue to  successively add Os(CO)₃(14n+0)fragment starting with Os we will generate a column of Tetracapped Series(S =14n -6, C_p = C⁴C) as follows: Os→ Os₂(CO)₃ → Os₃(CO)₆ → Os₄(CO)₉→ Os₅(CO)₁₂→ Os₆(CO)₁₅ → Os₇(CO)₁₈ → Os₈(CO)₂₁ → Os₉(CO)₂₄  → Os₁₀(CO)₂₇ and so on.  As can be seen from Table 3,Os₁₀(CO)₂₇ is a member of tetracapped series with its closo nucleus based on octahedral symmetry. We may symbolically express this as C_p = C⁴C[M-6]. In other words, it has a nucleus with an electron content equivalent to that of an octahedral cluster Os₆(CO)₁₉ or in the case of the main group elements, B₆H₆²cluster. Similarly, from Table 3,  Os₉(CO)₂₄ is tetra capped based on trigonalbipyramidcloso nucleus. That is, C_p = C⁴C[M-5], [M-5] = Os₅(CO)₁₆Ξ  B₅H₅^2― ,Os₈(CO)_{21 →}C⁴C[M-4], [M-4] =Os₄(CO)₁₃Ξ B₄H₄^2―,  Os₇(CO)₁₈→C⁴C[M-3], [M-3] =Os₃(CO)₁₀Ξ B₃H₃^2―,  Os₆(CO)₁₅  → C⁴C[M-2], [M-2] =Os₂(CO)₇Ξ B₂H₂^2―and Os₅(CO)₁₂→ C⁴C[M-1], [M-1] =Os(CO)₄ Ξ BH^2―.Using other points or ‘beads’similar capping and ordinary cluster series can be derived. ’The S = 14n-4 (Tricapped)series has the three first members as OsCO →Os₂(CO)₄→Os₃(CO)₇ with the corresponding electron content as (10, 24, 38). As can be seen, they also vary by 14 electron units. If n = 1, then 14n-4 = 14(1)-4 = 10 which corresponds to the electron content of OsCO fragment.  Also the Table 3 shows that CO molecule can be placed in the category of CLOSO series( 14n+2) as CO→ Os(CO)₄→Os₂(CO)₇ and so on. In terms of valence electron content this corresponds to 2→16→30. Again the change from one member to the next is 14 electron units. Indeed the CO obeys the 14n+2 rule since when n = 0, 14n+2 = 14(0)+2 = 2, the number of electrons one CO donates to a cluster. What is also fascinating is that the CO molecule also obeys the S = 4n+ 2 rule for n =2 (V = 10) of the main group element clusters already discussed. This links up nicely the parallel relationship between (14n +2 ↔ 4n+2) series. Finally, let us look at the three first members of the Monocap (14n) series namely, Os(CO)₃→Os₂(CO)₆→Os₃(CO)₉.The respective electron content is 14→28→42 with the series variation of 14 electron units.  If n = 1, then S = 14n = 14(1) =14 the valence electron content of Os(CO)₃ fragment.Indeed the Os(CO)₃ fragment is a member of  the 14n series. THE DIAGONAL RELATIONSHIP  The way the table is arranged reveals yet another interesting relationship of the cluster series.  For example consider the following diagonal relationship type of series. Let us begin with Os₄(CO)₁₆ and follow its path; Os₄(CO)₁₆ → Os₄(CO)₁₅→ Os₄(CO)₁₄→ Os₄(CO)₁₃→ Os₄(CO)₁₂→ Os₄(CO)₁₁→ Os₄(CO)₁₀→ Os₄(CO)₉→ Os₄(CO)₈→ Os₄(CO)₇→ Os₄(CO)₆→ Os₄(CO)₅→ Os₄(CO)₄→ Os₄(CO)₃ →Os₄(CO)₂→ Os₄(CO)→ Os₄. The stripping series showing a ‘naked’ cluster such as Os₄is quite interesting.Can the clusters of the series Os_n(n =2, 3, 4, 5, 6, 7, 8, 9, 10..)exist in the absence of supporting ligands?The above type of series may be called STRIPPING SERIES since at every step the CO ligand is stripped off. Some good work has been done that reveals the existence of stripping series^16-17.THE GENERATING FUNCTIONS OF SERIES AND CLUSTERS  When these carbonyl cluster series are scrutinized, it becomes clear that they have  inherent orderly simple  patters. Such patterns can easily be expressed by simple algebraic functions.  For instance, the Hypho Series (S =14n+8) can be generated by a simple mapping function, f(n) →(3n+4). Let us apply the mapping function to generate a few clusters as follows: f(0) →3(0) +4 = 4. This means that when there is no skeletal element, therefore we get 4CO ligands as members of the 4n+8 series. Since n = 0, then S = 14n+8 = 0+8 =8, the valence content of 4CO (4×2=8) ligands. When n =1, then f(1) →(3×1+4) = 7. This means we have generated the hypothetical chemical species Os(CO)₇which has also been obtained in the process of constructing the series table. For n =4, for example, we get f(4) →(3×4+4) = 16. This gives us the cluster member of Os₄(CO)₁₆ one of the carbonyl complex of osmium. It also belongs to Hypho Series (S = 14n+8). The generating function for Arachno Series (S = 14n+6) is f(n) →(3n+3), Nido Series (S =14n+4) is , f(n) →(3n+2), Closo Series (S=14n+2) is, f(n) →(3n+1), Monocap (S = 14) is, f(n) →(3n), Bicap(S= 14n-2) is f(n) →(3n+1), Tricap( S=14n-4) is f(n) →(3n+2) and Teracap(S =14n-6) is f(n) →(3n+3). Selected generating functions of Nido, Closo, Monocaped and Bicapped series as well as osmium carbonyl clusters produced up to n =12 are presented in Table7.

Table 7: Generating Functions of Selected Cluster Series

				CO
0	2	2CO	1	CO
1	5	Os(CO)5	4	Os(CO)4
2	8	Os2(CO)8	7	Os2(CO)7
3	11	Os3(CO)11	10	Os3(CO)10
4	14	Os4(CO)14	14	Os4(CO)13
5	17	Os5(CO)17	16	Os5(CO)16
6	20	Os6(CO)20	19	Os6(CO)19
7	23	Os7(CO)23	22	Os7(CO)22
8	26	Os8(CO)26	25	Os8(CO)25
9	29	Os9(CO)29	28	Os9(CO)28
10	32	Os10(CO)32	31	Os10(CO)31
11	35	Os11(CO)35	34	Os11(CO)34
12	38	Os12(CO)38	37	Os12(CO)37

0	0
1	3	Os(CO)3	2	Os(CO)2
2	6	Os2(CO)6	5	Os2(CO)5
3	9	Os3(CO)9	8	Os3(CO)8
4	12	Os4(CO)12	11	Os4(CO)11
5	15	Os5(CO)15	14	Os5(CO)14
6	18	Os6(CO)18	17	Os6(CO)17
7	21	Os7(CO)21	20	Os7(CO)20
8	24	Os8(CO)24	23	Os8(CO)23
9	27	Os9(CO)27	26	Os9(CO)26
10	30	Os10(CO)30	29	Os10(CO)29
11	33	Os11(CO)33	32	Os11(CO)32
12	36	OS12(CO)36	35	Os12(CO)35

 

MONOCP                                   BICP

S=14n                                          14n-2

F(n)→          3n                                            3n-1

Os                   CO Formula                           CO    Formula

Detrmining A Required Hypothetical Cluster Formular and the Simple Algebra of Clusters

Apart from generating members of the clusters series using generating functions such as those shown above, it is possible to create a simple formula to produce a required or targeted cluster carbonyl complex. Let us consider the following hypothetical examples.Let us take Os₃(CO)₁₂ complex as a starting material on which to build other carbonyl clusters. Let us further visualize adding 57 more fragments of the formula Os(CO)₃. The final cluster will have a molecular formula obtained by the following simple relationship F = Os₃(CO)₁₂ + 57 [Os(CO)₃] = Os₃(CO)₁₂+Os₅₇(CO)₁₇₁ = Os₆₀(CO)₁₈₃. The classification of this cluster can readily be identified using the 14n Rule¹⁸ as follows, n = 60, 14n = 14×60 = 840, V = 8×60+183×2 =846. Hence, the cluster belongs to S= 14n+6 (ARACHNO) Series.

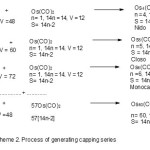
Clearly this is a form of an arithmetical series F = a₀+(n-1)d where a₀ =Os₃(CO)₁₂, n =58, d = Os(CO)₃ fragment. Thus, F = Os₃(CO)₁₂+(58-1)[Os(CO)₃] = Os₃(CO)₁₂+57[Os(CO)₃] = Os₃(CO)₁₂+Os₅₇(CO)₁₇₁ = Os₆₀(CO)₁₈₃ as derived earlier. Let us categorize the starting simple cluster, Os₃(CO)₁₂; n =3, 14n = 14×3 =42, V = 8×3+12×2 =48. Hence, the cluster belongs to S=14n+6 =V=48. It is therefore a member of Arachno Series. From Table3, the fragments can be categorized into series. Therefore, Os(CO)₃, n= 1(one skeletal element), 14n = 14(1) = 14, V =8+3×2 =14. Hence, S =14n =14 =V. Thus, the fragment is a member of S =14n Monocap series. Thus, Os(CO)₃ fragment is behaving like a ‘BEAD’ being utilized to create a long CHAIN or STRING  of  beads of clusters of the same series, in this case the ARACHNO series.Let us analyze this cluster growth in more details in terms of the following equations shown in Scheme 1.

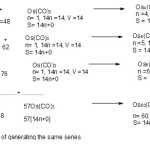Scheme 1  Click here to View scheme

 

The Growth of Clusters

A close analysis of Table 3 shows that there are two principal fragments responsible for producing osmium carbonyl clusters namely Os(CO)₃ (14n+0) and Os(CO)₂(14n-2). The repeated addition of Os(CO)₃ (14n+0)fragment produces an increase in cluster size)length without change in the type of series. This is illustrated and summarized in the example shown in Scheme 1. On the other hand, the addition of Os(CO)₂(14n-2) fragment introduces a cap to the chemical system in question. When a molecule being extended is a member of series below the closo series, the capping goes on till a closo cluster has been attained. After that the capping becomes centered on that closo unit. This is illustrated in Scheme 2 where the capping is based on a trigonalbipyramid unit.  As it can clearly be seen, there is no change in the type of series as it starts with Os₃(CO)₁₂(S=14n+6) and ends with Os₆₀(CO)₁₈₃(S=14n+6) for the successive addition of  57 Os(CO)₃(14n+0) fragments. Let us compare the above hypothetical example with a similar one but this time using the transforming fragment Os(CO)₂(14n-2). The final cluster formed will be given by F = Os₃(CO)₁₂ + 57 [Os(CO)₂] = Os₃(CO)₁₂+Os₅₇(CO)₁₁₄ = Os₆₀(CO)₁₂₆. This cluster can be categorized as follows, n = 60, 14n =14×60 = 840,V = 732, S = 14n-108. This can be written as S = 14n +54(-2). Hence the capping notation by this method derived from this series is given by C_p = C¹ + C⁵⁴ = C⁵⁵C[M-5]. This symbol implies the Os₃(CO)₁₂ starting simple carbonyl cluster was capped 57 times but 2 of those copings were utilized to create a Closo nucleus with a trigonalbipyramid entity symbolized as [M-5]. Since the nucleus is of Closo Series its generating mapping function is f(n) →(3n+1). Hence, [M-5] = f(5)→(3×5+1) = 16. This gives us the valence equivalent cluster of Os₅(CO)₁₆. This nuclear cluster has, in principle, a trigonalbipyramid shape. In other words, Os₆₀(CO)₁₂₆ is expected to be a huge carbonyl cluster of 60 skeletal atoms but hidden inside is another smaller cluster of a trigonalbipyramid(D_3h)symmetry. In Scheme 2, we can give a possible process of the formation of the giant cluster and the transformation of the cluster series.The addition of Os(CO)₂(14n-2) fragment decreases the code of the cluster by (-2). For instance, if the molecular system belongs to S = 14n+10 series, it will be converted into [14n+10-2] = 14n+8. The next addition generates 14n+6(hypho series) , then 14n+4(nido), 14n+2(closo), 14n(monocap), 14n-2(bicap). 14n-4(tricap), 14n-6(tetracap), and so on.In this way, the concept of cluster formation is more or less similar to that of POLYMERIZATION. An attempt to demonstrate the concept of cluster formation is illustrated in Shemes 1 and 2 as well as in Table 7.

 

Scheme 2  Click here to View scheme

 

But the fragment Os(CO)₂; n =1, 14n = 14, V = 8+4 = 12. Hence, the fragment is a member of the Bicap Series S =14n-2.As can be seen from Scheme 2, what is exciting in adding the fragment Os(CO)₂ is the corresponding successive decrease of the series by (-2).  For instance when the Os(CO)₂(14n-2)fragment is added to Os₃(CO)₁₂(14n+6) the product becomes Os₄(CO)₁₄(14n+4).&nbsp

Os₄(CO)₁₄ cluster has a tetrahedral geometry (k = 6). Continuation of adding Os(CO)₂(14n-2)fragment to Os₄(CO)₁₄(14n+4) produces Os₅(CO)₁₆(14n+2) cluster which has a trigonalbipyramid and belongs to a Closo family. Thus, the two Os(CO)₂(14n-2)fragments have resulted into the transformation of Os₃(CO)₁₂ Arachno cluster into a Closo one. After these two additions, the rest

of the 55 Os(CO)₂(14n-2) will all be utilized for capping to generate a giant cluster Os₆₀(CO)₁₂₆. It is quite clear that in the capping process, the 14n parameter remains constant, the change involves only the interactions of the outside digits in the series codes. With this observation, we can do the arithmetical additions of the outside digits to determine the final code of the cluster. In this case, we have to consider the changes of the code additions of (14n+6)+ 57(14n-2). In terms of the code addition, this will be equal to [14n+6+57(-2)]=(14n-108). This is indeed the cluster series code for Os₆₀(CO)₁₂₆ carbonyl complex. We also know that 14n represents Monocapping. Any extra capping after 14n is represented by (-2). Hence, -108 = 54(-2) represents another 54 cappings. Therefore, we can translate the code 14n-108 to mean 1 cap from 14n and 54 caps from (-108) giving us a total of 55 caps all together. For visual purposes we may represent a huge cluster with a smaller one inside shown in Figure 4.

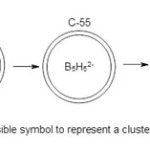Figure 4  Click here to View figure

 

Table 8: Generating Monocap Series (S =14n) with Os(CO)3(14n+0) Fragment  Click here to View table

 

Table 9: Generating Capped Series with Os(CO)2(14n-2) Fragment  Click here to View table

 

Classification of Carbonyl Clusters Using the Osmium Carbonyl Cluster Table

The above constructed carbonyl table(Table 3) is extremely useful in categorizing a carbonyl cluster into its type of series code.That is, to deduce whether a given cluster is a member of  klapo, hypho, arachno, closo, monocapped and so on. If a given cluster comprises of osmium and CO ligands only, the deduction is simple. It is a matter of tracing the formula of that cluster and determine its location in Table 3 and hence the code of the series is just on top of the table. Let us illustrate this idea using the table with the following osmium clusters. Starting with a simple oneOs₃(CO)₁₂ and doing a little calculation will quickly show you where it is located. For instance, looking for its lower members in the ordinary series, by removing Os(CO)₃ fragment we get the following: Os₃(CO)₁₂–Os(CO)₃→Os₂(CO)₉ ― Os(CO)₃→Os(CO)₆ and this places it in the ARACHNO family(14n+6).  In the stripping series, the next member on the diagonal is Os₃(CO)₁₂ ―(CO)→Os₃(CO)₁₁. In the capping series, its neighbor will be Os₃(CO)₁₂ + Os(CO)₂ →Os₄(CO)₁₄. Thus, with certainty, Os₃(CO)₁₂ is a member of Arachno series. We can also use the 14n rule which is exceedingly useful for the classification of large clusters which may not be in Table 3 as follows, n = 3, 14n = 14×3 = 42, valence electrons V = 3×8+12×2 = 48 and series S = 14n+6 =V (Arachno). This process is summarized in Scheme 3.

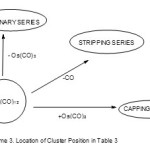Scheme 3  Click here to View scheme

 

Take Os₅(CO)₁₆ example. We can remove 4Os(CO)₃= Os₄(CO)₁₂fragments to determine the starting building block of its ordinary series. Thus,Os₅(CO)₁₆ ―Os₄(CO)₁₂  = Os(CO)₄. This places Os₅(CO)₁₆ in the Closo series (14n+2).  When there is a charge as in Os₆(CO)₁₈^2― cluster, the two negative charges are converted into its CO equivalent. In this case, (-2)  = 1 CO and the cluster becomesOs₆(CO)₁₉. Removal of 5Os(CO)₃ = Os₅(CO)₁₅ from Os₆(CO)₁₉ gives is the starting unit as Os(CO)₄. Clearly, Os₆(CO)₁₉ (Os₆(CO)₁₈^2― ) is a member of the closo series and since it has six skeletal atoms Os₆[M-6], they will take up an O_h symmetry. If a cluster has “guest atoms”or ligands other than CO, then the valence electron content of the cluster is converted into its osmium equivalent. For instance H₃Os₆(B)(CO)₁₆ its valence electron value V = 3+6×8+3+16×2 = 86. However the 6 Os atoms have a valence electron content given by Vos = 6×8 = 48. Hence the remaining electrons Vco = 86-48 = 38 will be converted into its CO equivalent ligands as 38/2 = 19. Hence, the osmium equivalent cluster will beOs₆(CO)₁₉ (Os₆(CO)₁₈^2―) which is closo and has an O_h symmetry. Consider Ir₄(CO)₁₂ cluster, V = 4×9+12×2 = 60, Vos = 4×8 =32, Vco = V-Vos =60-32 = 28 and number of CO ligands Nco =Vco/2 = 28/2 =14.  Hence, the osmium cluster equivalent is Os₄(CO)₁₄. The starting block in its ordinary series is given by Os₄(CO)₁₄ ― 3Os(CO)₃ →Os₄(CO)₁₄ ― Os₃(CO)₉ = Os(CO)₅. This places Ir₄(CO)₁₂ cluster in the Nido family (14n+4). For very large carbonyl clusters, their formulas get out of the range of the table. In that case, the 14n rule explained in our earlier work¹⁸ is very helpful.

Giant Python Clusters Swallowing Smaller Ones

Take Os₆(CO)₁₉ (closooctahedtral cluster) as a starting cluster on which others can be built. If 94 Os(CO)₂ fragments are added to it we will generate a huge cluster of the formula F = Os₆(CO)₁₉ + Os₉₄(CO)₁₈₈ = Os₁₀₀(CO)₂₀₇. Applying our method of classification, 14n = 14×100 = 1400, V = 1214. Hence this cluster belongs to S =14n-186 series.  The series may be written as S = 14n+93(-2). This has a capping given by the symbol C_p = C¹+C⁹³ = C⁹⁴C[M-6]. This symbol means that this will be a huge cluster with an [M-6] cluster embedded inside other 94 skeletal atoms. The [M-6] notation is a symbol to represent an octahedral nuclear cluster enclosed in the giant cluster of total 100 skeletal atoms. The cluster series code can also be derived from S =[(14n+2)+94(-2)] =[14n+2-188] =(14n-186) as obtained above. All the fragments have been utilized for capping purposes since the starting cluster is already a closo member.

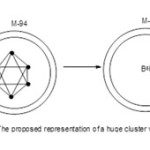Figure 5 Click here to View figure

 

The symbol [M-6] represents a closo cluster equivalent to Os₆(CO)₁₉ or B₆H₆^2―.The cluster Os₆(CO)₁₈ has attracted a lot of attention^19-20 probably due to its having the same number of CO ligands as Os₆(CO)₁₈^2― with the exception that it does not carry the two negative charges. Its shape is usually described as a monocapped cluster with respect to a trigonalbipyramid or a bicapped cluster with respect to a tetrahedral geometry. If we look at it in terms of series(see Table 3), we find that it is simply a member of mono-capped series (14n). This series is a unique one as 14 times the number of skeletal atoms gives a numerical result exactly the same as the number of valence electrons of the cluster. It may regarded as a hexa-mer of Os(CO)₃(14n) fragment. We can also write the series as Os(CO)₃(14n+0). Since the digit after 14n is 0, the various combinations of the same fragment will generate the same series. Let us generate some of its members up to n =10 to enable us have a feel of this type of series: Os(CO)₃→ Os₂(CO)₆→Os₃(CO)₉→Os₄(CO)₁₂→Os₅(CO)₁₅→Os₅(CO)₁₅→Os₆(CO)₁₈→Os₇(CO)₂₁→Os₈(CO)₂₄→Os₉(CO)₂₇→Os₁₀(CO)₃₀. It is also interesting to note that the ratio of n to number of CO s is 1:3. Hence, the series can be expressed as Os_n(CO)_3n ={Os(CO)₃}_n. This process is similar to the polymerization encountered  in organic chemistry involving fragments such as CH₂→n(CH₂) = (CH₂)_n. Since capping usually refers to a capping on a closo system, in case of Os₆(CO)₁₈ cluster, it implies capping will be on M-5 closo system which will be a trigonalbipyramid, Os₅(CO)₁₆ which is a member of its capping series. Indeed if we add up the two chemical species [Os₅(CO)₁₆ (14n+2) + Os(CO)₂(14n-2) = Os₆(CO)₁₈ [14n+2+(-2)] =  Os₆(CO)₁₈ (14n+0) = Os₆(CO)₁₈ (14n)] we generate the mono-capped cluster. We have seen 10 members of the 14n series in which Os₆(CO)₁₈ belongs. Such members are generated using Os(CO)₃(14n)fragment. We can also generate some members of its capping series by adding Os(CO)₂(14n-2) fragments. These are already given in Table 7 in the bicapped series column.

The Capping Symbol, CⁿC

The desire to understand clusters more stimulated the need to create a symbol to express capping. Consider the following osmium clusters, Os₆(CO)₁₈^2―(Os₆(CO)₁₉ octahedral, closo)→Os₇(CO)₂₁(Monocapped octahedral, closo)→Os₈(CO)₂₂^2―(Os₈(CO)₂₃)(Bicapped octahedral, closo)→Os₉(CO)₂₄^2―(Os₉(CO)₂₅)(Tricapped octahedral, closo)→Os₁₀(CO)₂₆^2―(Os₁₀(CO)₂₇)(Tetracapped octahedral, closo).The respective series are, (14n+2), (14n+0), (14n-2), (14n-4), and (14n-6). After pondering over these series, it was deemed a good idea to use, C¹ to represent mono-capped geometry. Hence, (14n) →C¹ , (14n-2) = [14n+1(-2)]. Since the capping starts at 14n, then any additional multiple of (-2) corresponds to an additional capping. Therefore, [14n+1(-2)]→C¹+C¹ = C². This simply means, the (14n-2) series is a Bicaped series (C²). Since these clusters are closo systems, the symbol becomes C²C. In this particular set of clusters, the capping is based on an octahedralcloso geometry of six skeletal elements. For further refinement of the introduced symbol of closo six skeletal elements, the symbol [M-6] was added. Thus, Mono-caaped symmetry based on octahedral is represented by C¹C[M-6] from (14n+0) series, Bicapped C²C[M-6] from [14n+1(-2)] = (14n-2) series, TricappedC³C[M-6] from (14n-4) =[14n+2(-2)] series→C¹+C² =  C³C[M-6] , and so on. It is also proposed that a symbol (M-n) could represent capping other than that based on non-closo system. For instance in the case of Os₆(CO)₁₈ we could refer to it as monocapped based on [M-5](closo) or bi-capped based on (M-4)(nido). The nido mapping generating function is given by F(n) →3n+2. For(4) = 3×4+2 = 14. Hence, Os₆(CO)₁₈  is bicapped onOs₄(CO)₁₄ cluster. The symbol [M-6] has been introduced to represent an octahedral clososystem in this case. We also know that the Generating function of a closo system is given by F(n) = 3n+1. This means that for n = 6, 3n+1 = 3×6+1 = 19 giving us the osmium cluster Os₆(CO)₁₉. Therefore, [M-6] is equivalent to Os₆(CO)₁₉ cluster that has  valence electron content of 86 for an octahedral geometry. Using the 14n rule or Table 3 above, the cluster Os₁₀(CO)₂₆^2― can be shown to belong to the series S =14n-6 = [14n+3(-2)] = C¹+C³ =  C⁴C[M-6]. If the series type of a cluster is determined, then the type of capping (Cp) can be deduced. Using this approach, the capping systems of small to medium to large clusters have readily been derived with amazing results. Consider the following clusters, Ru₈Pt(CO)₁₉^2―; n = 9, 14n =14×9 =126, V = 114, S = 14n-12 = 14n+6(-2). Hence the capping will be given by C_p = C¹+C⁶=  C⁷C[M-2]. This symbol means that 7 skeletal atoms will be involved in capping while the remaining two will form the closo nucleus. Following the same method, Os₁₇(CO)₃₆^2―(S = 14n-28) will have a capping given byC_p = C¹+C¹⁴ =  C¹⁵C[M-2].  In this case as well the nucleus will have 2 skeletal atoms while the remaining 15 will be capping the cluster the tiny closo nucleus. On the other hand, Ni₃₈Pt₆(CO)₄₈^6―; n =44, 14n = 44×14 = 616, V = 542, S = 14n-74, [14n+37(-2)], C_p = C¹+C³⁷ =  C³⁸C[M-6].  With this code notation derived from series, means that the skeletal cluster of 44 atoms has six of them with a closo octahedral symmetry surrounded

by 38 capping atoms. This fascinating result predicted from series is what is observed²¹. Furthermore, the octahedral inner core comprises of platinum atoms only²¹.  With series knowledge we have so far, it can it can be shown the symbol  C_p = C¹+C³⁷ =  C³⁸C[M-6] represents the valence electron content of the cluster as follows:[M-6] = Os₆(CO)₁₉ as already proved, C³⁸ = 38[Os(CO)₂] = Os₃₈(CO)₇₆. Therefore the cluster formula equivalent is given by F =  Os₆(CO)₁₉ + Os₃₈(CO)₇₆ = Os₄₄(CO)₉₅. The valence electrons of this cluster = 44×8+95×2 = 542 as calculated for Ni₃₈Pt₆ (CO)₄₈^6― complex. We can represent this giant cluster of six platinum closo octahedral nucleus by a ketch shown in Figure 6. Using series method, the cluster Pd₂₃(CO)₂₂L₁₀ where L = PEt₃, has a capping symbol C_p =C¹⁵C[M-8] and Au₆Ni₃₂(CO)₄₄^6― also has a capping symbol C_p =C²⁷C[M-11]. Clearly, the sizes of skeletal closonulearatoms varies widely. In these few examples we have  seen the range [M-2] to [M-11]. This reminds us of the notorious African pythons which can ambush, grab and swallow animals as small as rabbits and as large as antelopes. It does appear that these huge carbonyl clusters portray an image of pythons.

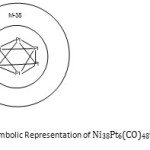Figure 6   Click here to View figure

 

The Algebra of Series

A closer scrutiny and study of the series in Table 3 clearly shows that the clusters series can easily be added and subtracted. This may have some implications on future synthetic work of carbonyl clusters. Let us look at the following illustrations based on the Table. As we have observed, the transition metal carbonyl series are based on 14n baseline. Therefore the digits after the 14n are the deciding factor on the type of product series that is theoretically expected to be formed. This means the digits can be added or subtracted using similar concepts found in algebra. This is illustrated by a few examples given in Table1O.

Table 10: Selected Examples Illustrating Addition and Subtraction of Series

	CLUSTER	OPERATION	CLUSTER	CLUSTER PRODUCT
1	Os5(CO)16	+	Os(CO)2→	Os6(CO)18
	14n+2	+	14n-2→	14n+[(2)+(-2)] = 14n+0 = 14n
2	Os5(CO)16	–	Os(CO)2→	Os4(CO)14
	14n+2	–	14n-2	14n+[(2)-(-2)] = 14n+4
3	Os4(CO)13	+	Os6(CO)16→	Os10(CO)19
	14n+2	+	14n-4	14n+[(2)+(-4)] = 14n-2
4	Os6(CO)19	–	Os2(CO)7→	Os4(CO)12
	14n+2	–	14n+2	14n+[(2)-(2)] = 14n+0 = 14n
5	Os6(CO)19	+	Os2(CO)3→	Os8(CO)22
	14n+2	+	14n-6	14n+[(2)+(-6)] = 14n-4
6	Os3(CO)12	+	Os5(CO)16→	Os8(CO)28
	14n+6	+	14n+2	14n+[(6)+(2)] = 14n+8
7	Os10(CO)27	–	Os3(CO)12→	Os7(CO)15
	14n-6	–	14n+6	14n+[(-6)-(+6)] = 14n-12
8	Os5(CO)19	+	Os10(CO)262―→	Os15(CO)46
	14n+8	+	14n-6	14n+[(8)+(-6)] = 14n+2

 

Isolobal Concept

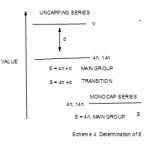
Table 3 also demonstrated that individual atoms, molecules and chemical fragments can be classified into series based on 14n or 4n rules.In order to greatly appreciate Hoffmann’s extremely important isolobal concept^12,22, it is equally important to briefly provide some highlights on how series are derived for re-emphasis as this is a new approach^13,14,18,. This summarized in Scheme 4 below.

Scheme 4  Click here to View scheme

 

The classification is based on 4n rule for the main group elements which obey the octet rule and 14n rule for transition metal atoms which obey the 18 electron rule.If the value of 4n is smaller than the valence value V of the atom, molecule or fragment in question, then the difference d between 4n and is added to ‘top up’ in order to be equal to the value of V. Then the series of the chemical species in question will be given by S = 4n +d = V for main group elements and S = 14n +d for transition metal carbonyl clusters. However, if 4n is greater than V then the difference between 4n and V must be subtracted in order to be equal to the value of the valence electrons V and hence the series will be given by S = 4n-d = V for main group elements and S = 14n-d for the transition metal carbonyl clusters. The borderline case occurs when 4n = V (main group) or 14n=V(transition metal). This is where capping begins in clusters( refer to Scheme 4). For S= 14n+d, these are series which are below mono-capped series such as closo, nido and arachno. For the series 4n-d or 14n-d, all these will be capping series beginning with (14n+0). Let us illustrate how the series of fragments are deduced. Consider, the C₂ molecule discussed earlier, n = 2, 4n = 8 and V = 8. Hence, S = 4n= 4n+0. For the monoatomic carbon, C, also S = 4n. However, for the C₂H₂; n =2, 4n = 8, V= 10 and so S = 4n+2 = V, when the C₂H₂ is fragmented into 2 CH units each unit carries 5 electrons. Thus, C₂H₂ (V= 10, S = 4n+2, n =2) → 2CH(V=5, S = 4n+1, n =1). What has happened in terms of series, when the molecule is fragmented, the baseline, 4n or 14n does not change except the digit after it. In short, C₂H₂ (S=4n+2) →2 CH₂(S = 4n+1). This in line with the algebra of series concept discussed above. Alternatively, the series of the fragment can be deduced by saying for CH₂, n =1, 4n = 4 and V = 5 and hence S = 4n+1. Likewise, forC₂H₄ (S=4n+4, n =2, V =12) →2 CH₂(S = 4n+2, n =1, V =6). For ethane,C₂H₆ (S=14n+6) →2 CH₂(S = 4n+3). For transition metal elements, 14n rule is used. The series for selected fragments from the main group elements and transition metals have been worked out and are presented in Table 11. This includes some fragments derived from Table 3. The table also puts more emphasis on the method of classifying molecules and fragments.

Table 11: Categorization of ChemicalFragments into Series

FRAGMENT	CATEGORIZATION
Os	14n-6
Os(CO)	14n-4
Os(CO)2	14n-2
Os(CO)3	14n
Os(CO)4	14n+2
Os(CO)5	14n+4

 

Fragment	n	4n	V	CLASSIFICATION
CH3	1	4	7	4n+3
CH2―	1	4	7	4n+3
CH2	1	4	6	4n+2
CH2+	1	4	5	4n+1
CH	1	4	5	4n+1

 

Fragment	n	14n	V	CLASSIFICATION
Mn(CO)5	1	14	17	14n+3
Tc(CO)5	1	14	17	14n+3
Re(CO)5	1	14	17	14n+3
Mn(PR3)5	1	14	17	14n+3
Cr(CO)5	1	14	16	14n+2
Fe(CO)4	1	14	16	14n+2
Os(CO)4	1	14	16	14n+2
CpRh(CO)	1	14	16	14n+2
Re(CO)4―	1	14	16	14n+2
Co(CO)3	1	14	15	14n+1
CpW(CO)2	1	14	15	14n+1

Fragment	n	14n	V	CLASSIFICATION
Mn(CO)5	1	14	17	14n+3
Tc(CO)5	1	14	17	14n+3
Re(CO)5	1	14	17	14n+3
Mn(PR3)5	1	14	17	14n+3
Cr(CO)5	1	14	16	14n+2
Fe(CO)4	1	14	16	14n+2
Os(CO)4	1	14	16	14n+2
CpRh(CO)	1	14	16	14n+2
Re(CO)4―	1	14	16	14n+2
Co(CO)3	1	14	15	14n+1
CpW(CO)2	1	14	15	14n+1

 

When we scrutinize Table 11, the fragments with the same (d) value as defined in Scheme 4 will be isolobal. Accordingly, for (d = 3), the following fragments are isolobal, CH₃,CH₂^―, Mn(CO)₅, Tc(CO)₅, Re(CO)_5, andMn(PR₃)₅, (d = 2), CH₂, Cr(CO)₅, Fe(CO)₄, Os(CO)4,C_pRh(CO), Re(CO)₄^―, (d = 1), CH₂⁺, CH, Co(CO)₃,and C_pW(CO)₂.Clearly, this approach of applying the series to classify chemical fragments, is extremely useful in understanding and explaining the isolobal concept.

Conclusion

As can be deduced from the Table 3, there are three main types of cluster series. The first typeis the one which we may call the ORDINARY series and this includes the familiar ones such as Arachno, Nido and Closo.  In this type of series the cluster  type remains constant and valence electrons change by 14 units  as the chain size or length increases. These utilize the Os(CO)₃(14n+0) FRAGMENT.  Then there are the CAPPING series. These involve the use of Os(CO)₂(14n-2)fragment as the chain length increases, the cluster type varies by12 electron units. Finally there are the STRIPPING series in which CO ligands are being removed. The cluster type varies but the number of skeletal elements constant.  But the valence electrons change by 2. Using the 14n and 4n rules, shows that there is close relationship between the transition metal carbonyl clusters and the corresponding ones of the main group elements especially the boranes. Many carbonyl clusters have a tendency of forming clusters centered around nuclear closo systems. The earlier work by Wade, Mingos with a bearing on series and Hoffmann on isolobal concept all based on Molecular Orbital Theory go along way in providing vital the pillars  in support of the validity of the 14n and 4n rules in explaining the carbonyl clusters, boranes, heteroboranes, Zintyl ion clusters, and the isolobal concept. Furthermore, the 18 electron rule and the octet (8) rule give a strong and firm foundation of the 14n and 4n rules in analyzing clusters.

Acknowledgement

The author wishes to acknowledge the University of Namibia and NAMSOV, Namibia for the financial and material support and my wife, Merab Kambamu Kiremire for her continued encouragement to write up this paper.

References

1. Wade, K. ,J. Chem. Soc., Dalton, 1971, 792-793.
2. Mingos, D. M. P., Nature Physical Science, 1972, 236, 99-102.
3. Cotton, F. A., Wilkinson, G., ‘Advanced Inorganic Chemistry’, 4^th Edition, John Wiley & Sons, New York, p317, 1980.
4. Rudolph, R. W.,Accounts Chem. Res., 1976, 9(12), 446-452.
5. Mingos, D. M. P., Nature Physical Science, 1972, 236, 99-102.
6. Mingos, D. M. P., Pure and Appl. Chem., 1991, 63(6), 807-812.
7. Scharfe, S, Fässler, T. F., Phil. Trans. R. Soc. A, 2010, 368, 1265-1284.
8. Greenwood, N. N., Earnshaw, A., ‘Chemistry of the Elements’, 2^nd Edition, Butterworth, Oxford, 1998.
9. Corbett, J. D., Angew. Chem. Int. Ed., 2000, 39, 670-690.
10. Hughes, A. K., Wade, K., Coord. Chem. Rev., 2000, 197, 191-229.
11. Douglas, B.,McDaniel, D. H.,Alexander, J. H., ‘Concepts and Models of Inorganic Chemistry’, 2^nd Edition, John Wiley and Sons, Inc., New York, 1983.
12. Hoffmann, R., Nobel Lecture, Chemistry, 1981.
13. Kiremire, E. M., Orient. J. Chem., 2015, 31(1), 293-302.
14. Kiremire, E.M., Orient. J. Chem., 2014, 30(4), 1475-1485.
15. Alexandrova, A. N., Boldyrev, A. I., Zhai, H., Wang, L., Coord. Chem. Rev., 2006, 250, 2811-2866.
16. Butcher, C. P. G., Dyson,P. J., Johnson, B. F. G., Khimyak, T., McIndoe, J. S., Chem. Eur. J. 2003,9(4),944-950.
17. Henderson, M. A.,Kwok, S., McIndoe, J. S., J. Am.Soc. Mass Spectrom.,2009, 20, 658-666.
18. Kiremire, E.M., Orient. J. Chem., 2015, 31(1), 387-392.
19. King, R. B., Inorg. ChimicaActa, 1986, 116, 99-107.
20. Teo, B. K., Longoni,G., Chung, F. R. K., Inorg. Chem., 1984, 23, 1257-1266.
21. Rossi, F., Zanello, P., Portugaliae Electrochimica Acta, 2011, 29(5), 309-327.
22. Hoffmann, R., Angew. Chem. Int. Edition, 1981, 21(10), 711-724.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.