¹³C and ¹⁷O NMR of Mono-Nuclear Carbonyls: A DFT Study

Introduction   

DFT was, earlier, applied by Schreckenbach et al [1-15] to study ¹³C and ¹⁷O NMR spectra of some mononuclear transition metal carbonyls. But the present work  would include the study of a number of NMR parameters such as Chemical Shifts of metal, the carbon and the oxygen species (δ M,δ¹³C, δ ¹⁷O), their Total NMR Shielding Tensors(σ M, σ ¹³C_,σ¹⁷O ) along with two diamagnetic contributions [diamagnetic core tensor{a} and diamagnetic valence tensor{b}] and four paramagnetic contributions [paramagnetic (b^) tensor{c}, paramagnetic (u^) tensor{d}, paramagnetic(s^) tensor{e} and paramagnetic gauge tensor(f). Algebraic sum of these 6 contributions was equal to their σ M, σ ¹³C, σ ¹⁷O respectively. The parameters like Fermi-contact (k) [10¹⁹ kg m^-2 s^-2 A^-2], spin-spin coupling (j) [p pm] were also obtained.

While the discussion on NMR of transition metal complexes [16, 17] encircled around ligand field theory [18], in the late 70s, a number of review articles were collected[19] on small molecules. Debrochere (1978) published a 100 page review containing 289 references [20] .But till then, no calculations on nuclear shielding and spin-spin coupling parameters were carried out. H F approach given by Nakatsuzi [21] presented a paper on the calculation of the above named parameters of the complexes was found lacking in high oxidation states d¹⁰ systems[22]. In 80s, the NMR shielding codes based on HFSor X α method were developed. It was afterward called DFT [23-25]^. In 1993, Kohn-Sham DFT [26, 27] employed IGLO [26-27] method to calculate nuclear shielding. Also, LORG approach [27] which was improved upon by GIAODFT [28] and CSGTmethods [29] was employed. Spin-spin coupling constant of complexes was first of all calculated by Malkin et al [30]. Dicken and Zieglar [31] calculated FC term [32] in1996. Later, SD term [33, 34] was included in spin- spin coupling values.

The 11  mono-nuclear carbonyls were  included in this study : [M (CO)₆](M=Cr, Mo, W), [V(CO)₆]^1- ,[M(CO)₆]¹⁺ (M=Mn , Re),  [M(CO₅)] (M=Fe, Ru Os),[Co(CO)₄]^1- and [Ni(CO)₄] . All these carbonyls obeyed the 18 electron rule.

Need of the Study

Three points necessitated this study as:

1. No computational studies were reported on the magnetic equivalence of COs. Only their spatial displacements/ stereo chemical equivalences were studied.
2. An important NMR parameter- Effective Spin Hamiltonian (H ^Spin) [17] which determines the energy of an NMR transition had, never, been calculated by DFT.
3. DFT had, hardly, been applied to NMR in ascertaining the pi-acid character of metal carbonyls though IR/ Raman techniques had abundantly been exploited.

Methodology

[3, 13, 32, 35, 36, 37]

ADF software was installed on Windows XP platform as “ADF jobs”. A new directory was created using “File menu” of ADF jobs.

After optimization of the carbonyl compound, different commands were filled into the software to obtain NMR and IR/Raman parameters as follows:

NMR Parameters

[36, 37]

The software was run by filling in certain commands like Single Point, LDA, Default, None, Collinear, Nysom using DZ or TPZ Basis sets. The Unrestricted command was left blank. Then “NMR Program” was run in three steps.

1. The Shielding Constants of  the constituents (σM ,σ ¹³C,σ ¹⁷O) were obtained from the “NMR Program” by clicking on  numbers of the  species and printing them along with “Isotropic Shielding Constants” and “Full Shielding Constants”. The Chemical Shifts (δ M, δ¹³C, δ¹⁷O) were obtained from their NMR spectra.
2. k and j values of  constituents were obtained from the same program by using a new Input File and printing numbers of Perturbing and Responding nuclei.
3. σ ¹³C_,  σ¹⁷O _, δ ¹³C, δ¹⁷O,k and j  of C and O of uncoordinated CO (g) were obtained by repeating the above mentioned two steps with reference values σ ¹³C (-34.44) and  σ¹⁷ O(-129.53).

IR and Raman Parameters

After Optimization, the software is run with Frequencies and Raman full to obtain values of frequencies of all the (3n-6) Fundamental vibration bands.

Results  

[I] Table: 1 contained Acronyms and their expanded forms. Tables: 2-3 gave the optimization[38,39]and thermal parameters of the carbonyls respectively.Table:4 contained eight NMR parameters: three shielding constants(σM,σ¹³C,σ¹⁷O ),three Chemical Shifts(δ M ,δ¹³C, δ ¹⁷O) and two Coordination Shifts(Δ δ ¹³C ^, Δ δ¹⁷O ) .Six  contributions consisting of two  diamagnetic and four  paramagnetic  terms of three parameters (α _M, α¹³C, α¹⁷O) were given in Tables:5-7[{a},{b}.{c},{d},{e}.{f}].Total values of  two diamagnetic and four paramagnetic contributions in σ M, σ¹³C and σ ¹⁷O were given in Table: 8. Table:9 represented Spatial and Magnetic Equivalence of CO groups. Table: 10 contained k and j parameters given by software and the H ^spin values as calculated from j values.

Table 1: Acronyms and Their Expanded Forms

DFT	Density Functional Theory
ADF	Amsterdam Density Functional
ZORA	Zeroth- Order Regular Approximation
LDA	Local Density Approximation
DZ/TPZ	Double Zeta/ Triple Zeta
GGABP	Generalized Gradient Approximation
GGABP	Generalized Gradient Approximation Becke  Perdew
Nysom	Normalized or True
H F	Hartree- Fock
HFS	Hartree-Fock-Dickson-Slater
IGLO	Independent or Individual Gauge  of Localized  Orbitals
LORG	Localized Orbitals Resonance Gauge
GIAO	Gauge Including Atomic Orbitals
CSGT	Continuous Set of  Gauge Transformation
SD/ FC	Spin-dipole/ Fermi-contact

 

Table 2: Optimization Parameters of Mononuclear Carbonyls  

Carbonyl (≈0.0D)	Point group	Total bonding  Energy	Total Energy: X c  (LDA) k J mole-1	Nucleus	I
[V(CO)6 ]1–	Oh	-9885.20	-309197.58(-289776.63, -19420.95)	51V	3.5
[ Cr(CO)6]	-do-	-9749.83	-317868.84(-298129.57,-19739.27)	53Cr	1.5
[ Mo(CO)6]	-do-	-9761.76	-504440.84(-479759.83, -24681.02)	95Mo	2.5
[W(CO)6]	-do-	-9991.96	-981514.64(-947053.82, -34460.82)	183W	0.5
[Mn(CO)6]1+	-do-	-8833.60	-326285.10(-306302.80,-19982.30)	55Mn	2.5
[Re(CO)6]1+	-do-	-9230.86	-999049.56(-964269.91, -34779.65)	185Re	2.5
[Co(CO)4]1-	Td	-6757.34	-279321.74(-263582.63, -15739.11)	59Co	0.5
[Ni(CO)4]	-do-	-6232.74	-289903.76(-273830.40, -16073.36)	61Ni	2.5
[Fe(CO)5]	D3h	-8029.69	302622.68(-284764.22,  -17858.46)	57Fe	1.5
[Ru(CO)5]	-do-	-7986.29	-496080.13(-473217.51, -22862.62)	101Ru	3.5
[Os(CO)5]	-do-	-8364.94	-984410.88(-951721.35, -32689.52)	187Os	1.5

*X c is made up of LDA and GGA components; which further contain Exchange and Correlation 

parts. Bonding energy is computed as an energy difference between the molecule and fragments. GGA is zero here.

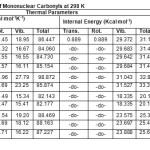Table 3: Thermal Parameters of Mononuclear Carbonyls at 298 K  Click here to View table

 

Table : 4. σ, δ and Δ δ [ppm] values of M, C and O in Mononuclear Carbonyls        Click here to View table

 

Table 5: Shielding Constants [p pm] of M, Diamagnetic and Paramagnetic Contributions

Carbonyl	σM( MCO)	Diamagnetic Contributions{a}              {b}	Paramagnetic Contributions{c}            {d}           {e}            {f}
[V(CO)6 ]1-	-141.68	1660.804,51.650	-250.309, -2096.566,493.643,-0.905
[Cr(CO)6 ]	-1428.92	0.000 , 1821.872	0.000, -3512.409, 262.589 , -0.975
[Mo(CO)6]	1328.44	3936.345,60.030	-745.997,-2900.566,979.771,-1.144
[W(CO)6]	4717.10	8530.161,198.232	680.920,-3665.371,-1027.367, 0.524
[Mn(CO)6]1+	-4718.18	1825.324,101.135	-229.740,-6590.544,717.941,-2.301
[Re(CO)6]1+	3296.33	8670.042,218.625	686.109,-5466.369, -812.461,0.385
[Co(CO)4]1-	-3771.98	1989.201,171.689	-117.023,-6423.724, 607.811,0.071
[Ni(CO)4]	-2050.46	2070.943,208.080	-132.181,-4552.960, 355.809,-0.147
[Fe(CO)5]	-5117.03	1907.276,134.245	-170.891,-7686.421,699.538,-0.779
[Ru(CO)5]	-993.92	4161.943,103.726	-574.583, -5456.581,771.062, 0.513
[Os(CO)5]	2061.72	8814.709,246.542	569.979, -6992.715, -578.172, 1.377

 

Table 6: Shielding Constants [p pm] of ¹³C, Diamagnetic and Paramagnetic Contributions

Carbonyl	σ13C(MCO)	Diamagnetic Contributions{a}           {b}	Para magnetic Contributions{c}           {d}         {e}            {f}
[V(CO)6]1-	-25.45	199.233,47.944	0.028 , -313.186, 39.704, 0.785
[Cr(CO)6]	-20.90	0.000 , 253.438	0.000 ,-301.057, 26.316 ,0.413
[Mo(CO)6 ]	-12.02	199.236, 50.566	0.080 ,-296.744, 34.131, 0.716
[W(CO)6]	-8.23	199.232 ,50.259	-0.018 ,-295.857,37.915, 0.241
[Mn(CO)6]1+	-20.05	199.233,50.516	-0.014,-304.470, 34.677,-0.001
[Re(CO)6 ]1+	-2.900	199.232 ,51.670	-0.030,-288.485,34.817,-0.116
[Co(CO)4]1-	-19.22	199.233 ,50.726	0.037,-309.605, 40.207,0.178
[Ni(CO)4]	1.12	199.233 ,51.411	0.031 ,-285.869,36.213,0.105
[Fe(CO)5]	-24.80(e)-56.30(a)	199.233 ,50.701199.233 ,51.687	0.007,-312.523, 37.832, -0.0600.031, -339.899,32.266,0.384
[Ru(CO)5]	-18.50(e)-36.17(a)	199.234 ,51.838199.234 ,53.295	0.045, -299.689, 29.641, 0.4140.096 , -316.614,27.040,0.775
[Os(CO)5]	-18.79(e)-30.6 (a)	199.233, 53.412199.233 ,51.367	-0.001,-313.307,29.599, 0.4460.008 ,-304.234, 34.814,0.020

 

Table 7: Shielding Constants [p pm] of ¹⁷O, Diamagnetic and Paramagnetic Contributions 

Carbonyl	σ 17O (MCO)	Diamagnetic Contributions{a}            {b}	Para magnetic Contributions{c}            {d}            {e}         {f}
[V(CO)6 ]1-	-45.97	269.471 ,133.899	-0.082, -392.033, -56.213 ,-1.060
[Cr(CO)6 ]	-74.97	0.000 , 397.850	0.000 ,-447.416, -24.582, -0.901
[Mo(CO)6]	-58.15	269.471 ,130.426	0.006 , -416.371, -41.090 ,-0.597
[W(CO)6]	-51.35	269.471,130.294	-0.003, -413.992, -36.338, -0.809
[Mn(CO)6]1+	-123.50	269.471, 127.036	0.019 , -490.879, -28.269, -0.862
[Re(CO)6]1+	-83.06	269.471,126.889	0.037, -454.952, -23.710 , -0.760
[Co(CO)4]1-	-34.20	269.472 ,134.157	0.030 , -385.614, -52.149 ,-0.091
[Ni(CO)4]	-42.90	269.472 , 130.513	0.048. -402.968, -39.838, -0.125
[Fe(CO)5]	-77.5 (e)-162.77(a)	269.472 , 130.303269.471 ,129.490	0.016 , -435.846, -40.978, -0.4170.016 , -533.743, -27.475, -0.532
[Ru (CO)5]	-82.00 (e)-117.25(a)	269.472 , 130.243269.471, 129.274	0.007 ,-435.040, -46.462, -0.223-0.007 , -489.099, -26.478,-0.406
[Os(CO)5]	-85.00(e)-104.50(a)	269.472 , 130.204269.471,  129.192	0.018 , -442.812, -41.543 ,-0.3400.001,  -481.733, -20.938, -0.479

 

Table 8: Total Diamagnetic, Paramagnetic contributions in σ M, σ13C and σ 17O [p pm]  Click here to View table

 

Table 9: Spatial and Magnetic Equivalence of COs in Mononuclear Carbonyls

Carbonyl	SpatiallyEquivalent COs	Magnetically Equivalent COs	Types of σ 13C  & σ 17O	No. of Spatially  Different COs
*[V(CO)6]1-	All	All	One	Same type of six COs
[Cr(CO)6]	-do-	3 types;2 in each type	-do-	-do-
[Mo(CO)6]	-do-	-do-	-do-	-do-
[W(CO)6]	-do-	-do-	-do-	-do-
[Mn(CO)6]1	-do-	-do-	-do-	-do-
[Re(CO)6]1+	-do-	-do-	-do-	-do-
*[Co(CO)4]1-	-do-	All	One	Same type of four COs
*[Ni(CO)4]	-do-	-do-	-do-	-do-
[Fe(CO)5]	2 types;3(e) and 2(a)	2 types ;3(e) and 2(a)	Two	2 types ;3(e) and 2(a)
[Ru(CO)5]	-do-	-do-	-do-	-do-
[Os(CO)5]	-do-	-do-	-do-	-do-

*All COs are both spatially and magnetically equivalent

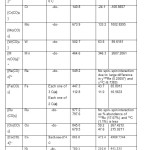Table 10: k, j   and H spin values of Nuclei in Mononuclear Carbonyls  Click here to View table

 

Discussion

The discussion was divided into eight headings as follows:

(A) As stated, the software gave a number of parameters which were further related a number of other parameters as follow:

(i)Sum of 6 contributions was equal to their σ M, σ ¹³C,_, σ ¹⁷O[p pm]  respectively.

σ M =Sum of 2 diamagnetic and 4 paramagnetic contributions of M   |

σ ¹³C =Sum of 2 diamagnetic and 4 paramagnetic contributions of ¹³C| [1]

σ ¹⁷O =Sum of 2 diamagnetic and 4 paramagnetic contributions of ¹⁷O|

(ii)The relation between (σ) and (δ) of carbon was given as:

 δ¹³C=181.1- σ ¹³C——————————————————————– [2]

(iii)δM and δ¹⁷O were numerically equal to σ M and σ ¹⁷O but with opposite signs

σ M =  – δ M |

| ———————————————— [3]

σ¹⁷O= – δ ¹⁷O |

(iv)The Coordination Shifts [Δ_δ¹³C, Δ_δ¹⁷O] and [σ ¹³C, σ¹⁷O] were related as:

Δ _δ¹³C₌ α¹³C (MCO) –(- 34.44) ————————————————— [4]

Δ _δ ¹⁷O ₌ α¹⁷O (MCO) – (-129.53) ————————————————- [5]

[B]Relative spatial displacements of constituting species were reaffirmed from shielding constants of the M, C and O [σM, σ ¹³C (M CO), σ ¹⁷O (MCO)] simply by the fact that the spatially equivalent species should have same values of shielding constants along with their constituting two diamagnetic and  four paramagnetic  terms respectively. All the ¹³C and ¹⁷O nuclei in each one of the four or six CO groups in T_d or O_h   possessed the same values of σ, _δ  and also the six contributing diamagnetic and paramagnetic quantities respectively. Therefore, all the four or six CO ligands were in the same spatial displacement, i.e. stereochemically equivalent around their respective central metal ion.It would be easy to conclude that that more the value σ¹³C,the lesser should be the value of Chemical shift (δ ¹³C) and more would be the value of Coordination Shift (Δ δ¹³ C) for a given stereochemistry of the carbonyls as illustrated below:

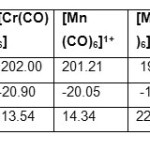Table 11 Click here to View table

 

[C] In D_3h stereochemistry, each one of the three ¹³C and ¹⁷O  had the same values of σ¹³C, _δ¹³C,σ¹⁷O and _δ¹⁷O along with their six contributing terms respectively; meaning thereby that the three COs were  stereo chemically equivalents. Each one of the remaining two COs also possessed same values of σ¹³C, _δ¹³C,σ¹⁷O and _δ¹⁷O along with their contributing terms respectively. But these values were quite different from those of the other three CO s. Thus these two COs were different from the other three COs spatially*.

The values of 8 parameters : σ M, δ M, σ ¹³C, δ ¹³C, Δ δ¹³C,  σ ¹⁷O, δ ¹⁷O and Δ δ¹⁷O [ pp m] for the11 mononuclear carbonyls were given in Table:4. The more the value of σ ¹³C,the lower was the Chemical shift (δ¹³C) and higher was the Coordination Shift (Δ δ ¹³C) for any stereochemistry. A positive Δ δ ¹³C is reported in O_h geometry which confirmsthe back-acceptor nature 0f CO. The difference between σ ¹⁷ Ovalues of carbonyls and the σ ¹⁷O of  CO (g) was noted. This positive** shift in Δ δ¹⁷ O also confirmed the transfer

*s p³d hybridization in a trigonal bipyrimidal geometry is supplemented by the prolate d_z² orbital having two opposite major lobes (m=0). A pair of opposite vertices [40] (X–M–X angle =180°) makes trigonal bipyramid a prolate polyhedron. Carbonyls occupying these two vertices have more electron density than the other three lying ^ to these two.  **Negative in [Fe (CO) ₅].    

of some electron density from C to O in carbonyls.

With two different types of spatially equivalent CO groups (e, a), the five   coordinate D _3h  carbonyls showed two types of σ ¹³C and σ ¹⁷O  values. Accordingly, two values of coordination shifts called Δ δ¹³C_a andΔ δ¹³C_e were obtained. Relative order of Δ δ¹³C_e in the five coordinate carbonyls is given as:

[Fe (CO)₅]˂ [Ru (CO)₅] ≈ [Os (CO)₅]

Δ δ¹³C_a follows the order:

[Fe (CO)₅]˂ [Ru (CO)₅] ˂ [Os (CO)₅]

[D]As shielding constant (σ) of a nucleus was directly related to its electron density, any change in its σ value would serve as an indicator of change in electron density on it. So, if CO were to act as a back acceptor, σ ¹³C of metal carbonyls should become more than σ ¹³C of CO (g). Some of the increased electron density on carbon was transmitted to oxygen to cause an increase in electron density on oxygen. So σ ¹⁷O would also increase. The NMR results corroborate with results obtained from their IR/Raman parameters in confirming their π – acid character as follows:

π-  ligand CO would donate electron density to the metal via a dative σ bond (OC → M) .Simultaneously, there would be a π back donation from the filled d orbitals of metal (OC ←M) to energetically favorable and geometrically suitable vacant π* molecular orbitals of CO. The effect being synergic should cause a decrease in carbon oxygen double  character  and, thus, a decrease in n_CO in  carbonyls with respect to  CO(g) having  n_CO= 2143 cm^1- was expected if C O was  to act as a back pi- acceptor. A comparison of σ ¹³C, δ ¹³C, Δ δ ¹³C and n_CO

(cm^-1)values of the 6 and 5 coordinate(axial) carbonyls in the  following  table lead to the conclusion that as the Chemical Shift(δ¹³C)decreased,n_CO(cm^1-) would  increase[41-48] to decrease  the capacity to back accept  electron cloud by CO.

Parameters[ p pm]	[V(CO)6]1-	[Mn (CO)6]1+	[Re(CO) 6]1+
δ 13C	206.50	201.21	184.01
σ 13C	-25.45	-20.05	-2.9
Δ δ 13C	8.99	14.34	31.54
nCO	2020.0	2192.0	2197.0
Parameters	[Cr(CO)6]	[Mo(CO)6]	[W(CO)6]
δ 13C	202.00	193.12	189.33
σ 13C	-20.90	-12.02	-8.23
Δ δ  13C	13.54	22.42	26.21
nCO	2118.7	2120.7	2126.2
Parameters( Equatorial)	Fe (CO) 5	Ru (CO) 5	Os(CO) 5
δ 13C	205.91	199.63	198.89
σ 13C	-24.81	-18.50	-18.79
Δ δ 13C	9.63	15.92	15.65
nCO	2022.0	2035.0	2036.0
π acceptor strength in all	Maximum	Less	Least

 

[E](i) Another important element of NMR symmetry was called the “magnetic equivalence” of nuclei .Enantiotopic or homotopic nuclei though possessed the same chemical shift (δ), but might not necessarily be magnetically equivalent. Two magnetically equivalent nuclei would have the same values of σ, δ, k and j with other nuclei of the molecule in addition to having same values among themselves .Coupling between symmetry equivalent and magnetically nonequivalent nuclei would affect the appearance of NMR spectrum while coupling between both the symmetry and magnetically equivalent nuclei had no effect NMR spectra.

[ii] With same σ ¹³C, δ¹³C, k and j values, the  four COs were both spatially and magnetically equivalent in T_d .Again, the six CO groups in [V (CO) ₆]^1- were both spatially and magnetically equivalent with the same σ ¹³C, δ ¹³C, k and j values. But the six COs in the remaining (O_h) mono-nuclear carbonyls were only spatially equivalent with same   σ ¹³C, δ ¹³C values as they possessed different k and j values. They were of three types. Each type having two CO groups possessed both spatial and magnetic equivalence. The three types of CO pairs had the same set of four parameters respectively between themselves and with remaining four CO groups though the set of four COs show different values from the previous set of two COs.

[iii] The five COs (D_3h) were neither spatially nor magnetically equivalent as they did not have the same set of four parameters. They consisted of two sets. The first set with two COs (a) and the second  with three COs (e) showed both the spatial and magnetic equivalence among themselves as either type possessed same set of values of four parameters among its own members and also with  members of other type of CO groups though the two sets have different values of these parameters.

[F] (i) Spin-spin coupling (j) was field-independent  and mutual (j _AB = j _BA).It  was affected by the nature of solvent ; metal−ligand bond distances and was transmitted through bonding electrons with its magnitude falling off rapidly with the increase in number of intervening bonds. Its sign was decided as: “it was positive if energy of A was lower when B had opposite spin as A (α β or β α), and negative if energy of A was lower when B had same spin as A (α α or β β )”.

(ii) The parameter (j) was related to another important NMR called Effective Spin Hamiltonian (H ^Spin). It was a mathematical expression that would determine the energy of an NMR transition. It term “effective” meant that its solutions reproduced nuclear magnetic energy levels in a molecular system without reference to electrons. In a fictitious absence of surrounding electrons, the shielding constants and indirect spin-spin coupling constants would vanish leaving the NMR spectrum to be determined by Nuclear Zeeman Term and direct dipolar coupling.  (H ^Spin) values of the metal ions and the bonded carbon atoms were related to their j [p pm] values as given below [6] ⁽¹⁷⁾.

H ^Spin ₌6.023j _{A B}. I_A. I_B.MHz mol^-1 _{———————————————- ———-}   [6]

Spin Hamiltonian [H ^Spin] values of the metal and the bonded carbon atoms of the eleven carbonyls are calculated by applying [5] (Table: 10).

[G]Individual values of 6 diamagnetic and paramagnetic quantities in σ _M,σ ¹³ C and σ ¹⁷O and their sums were given in Tables: 5-8 respectively.

[H] Table: 9 showed spatial displacements of 4, 5 or 6 CO groups around the metal.

Conclusions

The originality and relevance of present work and how it moved the body of  scientific knowledge forward would lie in the fact that it reaffirmed the relative spatial displacements of CO groups; classified them according to their spatial and magnetic equivalence; lent credence to π – acid character of carbonyls by corroborating with their IR/Raman studies and hence justified the need of taking up this study.

Acknowledgements                                                                           

Authors gratefully acknowledge the kind and willing cooperation of Mr. Sunil Chawla [sunil@seascapelearning.com] of ADF (http://www.scm.com).They feel indebted to Mr. S.R. Heer, Chief Engineer (Retd.), North Zone, Doordarshan, New Delhi (India), for his invaluable cooperation in the installation and  smooth working of the ADF software.

References

1. Ruiz-Morales, Y.; Schreckenbach, G.; Ziegler, T. J. Phys. Chem. 1996 100, 3359−67.
2. Schreckenbach, G.; Ziegler, T.; Li, J. Int. J. Quantum Chem. 1995 56, 477−88.
3. Schreckenbach, G.; Ziegler, T. J. Phys. Chem. 1995 99, 606-11.
4. Li, J.; Schreckenbach, G.; Ziegler, T. Inorg. Chem. 1995 34, 3245−52.
5. Li, J.; Schreckenbach, G.; Ziegler, T. J. Am. Chem. Soc. 1995 117, 486−94.
6. Li, J.; Schreckenbach, G.; Ziegler, T. J. Phys. Chem., 1994 98, 4838−41.
7. Popenova, S.; Mawhinney, R. C.; Schreckenbach, G. Inorg. Chem. 2007 46(10), 3856-64.
8. Schreckenbach, G. Inorg. Chem. 2002 41(25), 6560-72.
9. Schreckenbach, G. Inorg. Chem. 2000 39(6), 1265-74.
10. Schreckenbach, G. J. Chem. Phys. 1999 110(24), 11936.
11. Schreckenbach, G.; Ziegler, T. J. Phys. Chem.A. 1997 101(18), 3388-99.
12. Gisbergen, S. J. A.; Snijders, J.G.; Baerends, E. J. Comp. Phy. Commun. 1999 118, 1191138.
13. Schreckenbach, G.; Ziegler, T. Int. J. Quantum Chem. 1997 61(6), 899-918.    
14. Patchkovskii S. and Schreckenbach G. Calculation of EPR g-Tensors with Density Functional Theory”, in, “Calculation of NMR and EPR Parameters: Theory and Applications”, M. Kaupp, M. Bühl, V. G. Malkin (Eds.), Wiley VCH, pp. 505−32
15. Liu, Z.; Li, Q. S.; Xie, Y.; King, R. B.; Schaefer, H. F. III. Inorg. Chem. 2007 46(5), 1803-16.
16. Autschbach J. Struc. Bond. 2004 112, 1-43.
17. Ballhausen C. J. Molecular Electronic Structures of Transition Metal Complexes. Mc Gray -Hill, London (1979).
18. Pyykko P. Theory of NMR Parameters From Ramsey to Relativity, 1953 to 1983-in Calculation of  NMR and EPR Parameters -Theory and Applications,  p.7-19 Wiley-VCH, Weinheim (2004).
19. De Brouchere G. Adv. Chem. Phys. 1978 37, 203-304.
20. Tossel J. A. Kluwer, Dordrecht. Nuclear Magnetic Shielding and Molecular Structure (1993).
21. Bieger, W.; Seifert, G.; Eschrig, H.; Grossmann G. Chem. Phys. Lett. 1985 115, 275-80.
22. Freier, D. G.; Fenske, R. F.; Xiao-Zheng. J .Chem. Phys. 1985 83, 3526-37.
23. Malkin, V. G.; Zhidomirov, G. M. Zh. Strukt. Kim. 1988 29, 32-36.
24. Malkin, V. G.; Malkina, O. L.; Salahub, D. R. Chem. Phys.  Lett. 1993 204, 80-86.
25. Malkin, V. G.; Malkina, O. L.; Salahub, D. R. Chem. Phys. Lett. 1993 204, 87-95.
26. Arduengo, A. J.; Dixon, D. A.; Kumashero, K. K.; Lee, C.; Power, W. P.; Zilm, K. W. J. Am. Chem. Soc. 1994 116, 6361-67.
27. Rauhut, G.; Puyear, S.; Wolinski, K.; Pilay, P.  J. Phys. Chem. 1996 100, 6310-16.
28. Cheeseman, J. R.; Trucks, J. W.; Keith, T. A.; Frisch, M. Chem. Phys. 1996 104, 5497-5509.
29. Malkin, V. G.; Malkina, O. L.; Salahub, D. R. Chem. Phys. Lett. 1994 221, 91-99.
30. Dixon, R. M.; Zieglar, T. J. Phys. Chem, 1996 100, 5286-90.
31. Autschbach, J.; Zieglar, T. J. Chem. Phys. 2000 113, 936-47.
32. Helgaker, T.; Watson, M.; Handy, N. C. J. Chem. Phys. 2000 113, 9402-09.
33. Sychrovsky, V.; Grafenstein, J.; Cremer, D. J. Chem. Phys. 2000 113, 3530-47.
34. Wolff, S. K.; Ziegler, T. J. Chem. Phys. 1998 109, 895.
35. Singh, H.; Bhardwaj, A. K.; Sehgal, M. L.; Ahmad, I. Oriental J. Chem. 2015 31(2), 671-79.
36. Singh, H.; Bhardwaj, A. K.; Sehgal, M. L.; Javed, M.; Ahmad, I. Oriental J. Chem. 2015 31(2).
37. Baerends, E. J.; Branchadell, V.;  Sodupe, M. Chem. Phys. Lett. 1997 265, 481-89.
38. Lipkowitz, K. B. and Boyd D. B. Kohn-Sham Density Functional Theory: Predicting and Understanding Chemistry”, in Rev. Comput. Chem. 15. pp.1-86, Wiley-VCH, N.Y. (2000).
39. King, B.R. Coordination Chem. Rev. 2004 197, 141–68.
40. Mclean, R. A. N. Can. J. Chem. 1974 52, 213-15.
41. Abel, E. W.; Mclean, R. A. N.; Tyfield, S. P.; Braterman, P. S.; Walker, A. P.; Hendra, P. J.  J. Mol. Spectros. 1969 30, 29-50.
42. Bigorgne, M. J. Organometal .Chem. 1970 24, 211.
43. Jones, L. H.; Mcdowell, R. H.; Goldblatt, M.; Swanson, B. I. J. Chem. Phys. 1972 57, 2050.
44. Edgell, W. F.; Lyford, J. IV. J. Chem. Phys. 1970 52, 4329.
45. Edgell, W. F.; Lyford, J. J .Am. Chem. Soc. 1971 93, 6407.
46. Bouquet, G.; Bigorgne, M. Spectrochim. Acta. 1971 27A, 139-49.
47. Calderazzo, F.; Eplattenier, F. L. Inorg. Chem, 1967 6, 1220.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.