Predicting ESR Peaks in Copper (II) Chelates Having Quadrupolar Coordinating Sites by NMR, ESR and NQR Techniques: A DFT Study

Introduction

Eight Cu(II) complexes such as [Cu(en)2]2+, Cu(teta)]2+, [Cu(tepa)]2+, [Cu(peha)]2+, [Cu(deta)X2] (X= Cl, Br, I, NCS) having poly-dentate ligands of a class called polyethylene polyamines (en, deta, teta, tepa, peha) and six other complexes like [Cu(gly)2], [Cu(edta)]4- , [Cu (tpy)X2] (X= Cl, Br, I, NCS) with other chelating ligands (gly, edta and tpy) having coordination number 4, 5 and 6 respectively were studied.

Enough work had already been reported on (en) and (edta) complexes [1-7]; only some wok was available on (tpy) complexes [8]while a little was known about polyethylene polyamines and five coordinate Cu (II) complexes [9]. This limitation arose from the fact that such complexes with a large number of spatially different NMR and ESR active nuclei were adversely affected by the presence of both the large Jahn-Teller effect and the high value of spin-orbit coupling constant of λ Cu (II) (-830.0 cm-1) [10-11].

This prompted us to take up this study by using DFT (Density Functional Theory) implemented by ADF (Amsterdam Density Functional) 2010.02 as it allowed us to select the interacting nuclei at our will [12-18]. We selected 63Cu, 14N, 35Cl, 79Br, 127I but omitted 1H. It was primarily due to the reason that all the selected nuclei possessed quadrupole (I ˃ ½) and were directly bonded with Cu(II) while the protons, with no quadrupole were two and more bonds away from the metal ion. This would cause j-j coupling to fall and so would be the interaction between the metal ion and the protons.

During the last decade, DFT calculations were often used on small molecule molecules. Although, all electron approaches might be carried out for simpler molecules, yet valence electron approaches considered molecules to be treated without significant loss in either rigor or accuracy. The quasi relativistic and more recent ZORA to Dirac equation approach implemented in ADF represents one such method where relativistic terms treat valence electrons in the field of a frozen core of relativistic atomic wave functions. Also, DFT had enabled us to have a deeper understanding of the relation between the magnetic parameters and electronic and geometrical structures of molecules. As ESR spectra was related to electronic structure and geometry of a system, DFT could  provide an alternative to the traditional Hartree-Fock(HF) and post-HF approaches to ESR calculations. Thus, its ability to include the effects of electron correlation had, over the last years, brought DFT to the forefront in the field of calculating ESR parameters.

While the discussion on NMR of transition metal complexes encircled around ligand field theory, in the late 70s, a number of review articles were collected on small molecules [19-20]. De Brouchere (1978) published a100 page review containing 289 references [21]. But till then no calculations on nuclear shielding and spin-spin coupling parameters was carried out. H F approach, given by Nakatsuzi did present a paper on calculation of NMR parameters of complexes [22],but it was found lacking in high oxidation states d10 systems [23]. In 80s, NMR shielding codes based on HFSor X α method were developed. It was later called DFT [23-25]. In 1993, Kohn-Sham DFT employed IGLO method to calculate nuclear shielding [26-27]. LORG approach [28] as improved upon by GIAODFT [29-30] and CSGT methods [31] was employed. The spin-spin coupling constants of the metal complexes were first of all calculated by Malkin et al. [32]. In 1996, Dickson and Zieglar [33] calculated FC term [34] by finite-perturbation approach. Later on, SD term [35-36] was also included in spin- spin coupling values.

The software gave both the ESR [(Hyperfine coupling Constant (A ten)], NQR parameters [Nuclear Quadrupole Coupling Constant (NQCC) and asymmetric constant()]from its “ESR/EPR Program” while Shielding constants (σ) and Chemical shifts (δ) of copper(II) and the Coordinating Atoms (CA) of ligands were calculated by another program called “NMR/EPR Program”.

Theoretical Basis of Prediction of ESR Peaks
Method evolved to theoretically predict the exact number of ESR peaks in chelating Cu(II) complexes which, hitherto, was not attempted had been summarized as follows:
I. The unpaired electron of 63Cu(II) may undergo hyperfine interaction with coordinating 14N and X= 35Cl, 79Br, 127Iof ligands as all have appreciable natural abundances.
II. The presence of a large Jahn-Teller effect generally allowed hyperfine interaction. Therefore, peaks should arise both from 63Cu(II) and 14N, 35Cl, 79Br, 127Iof ligands.
III.63Cu(II)(I=3/2) would always give a quartet according to the relation:

(2 IM +1) ………………………………………………………………………………. (a)

IV. The five parameters such as A ten, NQCC, , σ , δ were obtained from the software. If these parameters possessed the same values for the [CA], then ligands would be spatially equivalent otherwise non equivalent.

VKnowing spatial nature of ligands, the number of peaks was predicted as follows:

(a) Suppose ICA was the nuclear spin of coordinating atoms of ligands and all the n ligands were spatially equivalent then the number of lines obtained were:

(2 n ICA +1) …………………………………………………………………………… (b)

(b) When n1 ligands were spatially of one type; n2 are of the other type and so on, then number of lines observed were:

(2 n1 ICA+1)(2n2 ICA+1)(2 n3 ICA+1) …………………………………………………. (c)

(c) All n spatially nonequivalent ligands would show the lines equal to:

(2 ICA+1) n ……………………………………………………………………………… (d)

As there was a considerable overlapping of ESR lines due to different reasons, the experimentally observed number of lines might be less than theoretically predicted lines. Also, when the predicted number of lines was large and Aten values of species undergoing hyperfine interaction were very small, they may merge to give a continuum.

Further, if A ten of Cu(II)was of higher value than those of CA of ligands, then first a large quartet from Cu(II) should be considered .This might, further, split into a number of lines by CA of ligands if a hyperfine interaction was possible. Conversely, if the CA of ligands possessed higher Aten value/s, then, we should first calculate number of lines obtained from the ligands. Each line of the ligands, may, then split into a quartet from Cu(II) due to hyperfine interaction between Cu(II)and ligands.

Methodology

Obtaining ESR and NQR parameters

After optimization of complexes, the software was run by Single Point, LDA, Default, Spin Orbit, Unrestricted, None, Collinear commands using DZ or TPZBasis sets with Nosymsymmetryin its “ESR/EPR Program” to obtain ESR (Aten) and NQR (NQCC,) parameters for the Cu(II) and the coordinating atoms (14N, 35Cl, 89 Br, 127 I) of the ligands [37-40].

Obtaining NMR Parameters

The σ and δ values of Cu (II) and 14N, 35Cl, 89 Br, 127 Iof ligands were obtained from “NMR/EPR Program” by the above commands except for replacing Spin Orbit by None [29, 41-42].

Results

Table: 1 and 2 gave expanded forms of the names of the ligands, acronyms used , optimization parameters giving the bonding energies, the total energies (Xc) including their LDA components consisting of Exchange and Correlation parts [43-44]. Tables: 3-4 contained values of A ten, NQCC, , σ, δ of Cu(II) and the CA along with the spatial nature of ligands for the fourteen Cu(II)complexes.

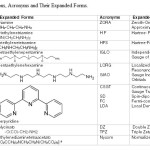Table1: Abbreviations, Acronyms and Their Expanded Forms.  Click here to View table

 

Table2: Optimization Parameters of Copper (II) Complexes

Complex	Point	Dipole	Total bonding	Total Energy :X c [kJ mol-1 ]
	group	moment	energy	LDA(Exchange; Correlation)
[Cu(gly)2]	C2	11.0	-10851.04	-338936.63
				-319322.20; -19614.43
Cu(edta)] 4-	C2	10.3	-19296.54	-497280.87
				-465641.17; -31639.70
[Cu(en)2]2+	C1	1.4	-11461.20	-294532.08
				-277441.03; -17091.06
[Cu(teta)]2+	C1	3.0	-14070.64	-320541.62
				-301291.69; -19249.94
[Cu(tepa)]2+	C1	2.2	-18061.38	-364494.57
				-341574.58; -22920.00
Cu(peha)] 2+	C1	2.2	-19850.46	-408474.95-381881.65; -26593.31
[Cu(deta)Cl2]	Cs	13.3	-11681.36	-417048.89
				-394474.78; -22574.11
[Cu(deta)Br2]	Cs	13.3	-12168.69	-743708.66
				-711425.03; -32283.63
[Cu(deta)I2]	Cs	13.2	-23777.60	-1202228.22
				-1159801.77; -42426.45
Cu(deta)(NCS)2	Cs	12.5	469.66	-460842.42
				-434423.66; -26418.76
[Cu(tpy)Cl2]	C2v	8.04	-20756.01	-552275.99
				-519159.50; -33116.50
[Cu(tpy)Br2	C2v	7.9	-21266.37	-878917.74
				-836093.81; -42823.93
[Cu(tpy)I2]	C1	7.4	-32800.17	-1337425.22
				-1284459.56; -52965.66
[Cu(tpy)(NCS)2]	Cs	4.5	-8767.54	-596097.26
				-559133.50; -36963.76

 

Discussion

No doubt, ESR of Cu (II) complexes had been extensively studied at room temperature, but the experimental determination of number of its ESR peaks having a large number of spatially different ESR active nuclei was cumbersome.

Table for ESR, NQR and NMR Parameters of Cu (II) and N of Copper (II) Polyethylene polyamines Complexes

Table: 3 contained A ten , NQCC, , σ , δ values of the parameters of Cu(II) and the Coordinating Atoms(CA) of the ligands for [Cu(gly)2], [Cu(edta)]4- and [Cu(L)]2+ ( L=en, teta, tepaandpeha).Their ESR discussion was divided into four parts:

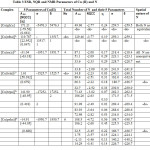Table3: ESR, NQR and NMR Parameters of Cu (II) and N  Click here to View table

 

Number of ESR Peaks in [Cu (gly)2] and[Cu(edta)]4-

In [Cu(gly)2] and [Cu(edta)]4-, both the coordinating N possessed same values of the five parameters respectively to confirm their spatial equivalence. In [Cu(gly)2] each line of a quartet of Cu(II)with higher Aten split into a quintet from two equivalents N having lower Aten values.Conversely, in [Cu (e d t a)] 4- each line of the quintet from the two equivalents N with higher A ten split into a quartet from Cu (II)with smaller Aten.

Number of ESR Peaks in [Cu(en)2]2+ and [Cu(teta)]2+

In [Cu(en)2]2+ and [Cu(teta)] 2+, all the four coordinating N were spatiallynon equivalent as all the five parameters of each N differ from one another. Again, in both the complexes, A ten values of all the four N atoms were higher than that of Cu(II).So ESR spectrum of eachgives 81 lines(c); each line splitting into a quartet from Cu (II).

Number of ESR Peaks in [Cu (tepa)]2+

In [Cu (tepa)]2+,one N of highest Aten gave a triplet with each line further splitting into a quartet from Cu(II) to give three quartets whose each line was then split into 81 lines (c) from remaining four non equivalents N having lower Aten values.

Number of ESR Peaks in [Cu (peha)] 2+

In [Cu(peha)]2+ , the three nonequivalent N withhighest Aten values gave 27(c) lines with each line further splitting into a quartet from Cu (II) to give 27 quartets. Each line of these quartets again split into 27 lines(c) from the remaining three non equivalents N having smaller Aten than Cu (II).

Table for ESR and NMR Parameters of Cu (II), N and X (Cl, Br, I, NCS) of [Cu (deta) X2] Complexes

Table: 4 gave A ten, NQCC, , σ, δ values of the parameters of Cu(II) and the CA for [Cu (deta) X2] (X= Cl, Br, I, NCS).All these complexes had the same symmetry symbol (Cs). Their ESR discussion was divided into four parts:

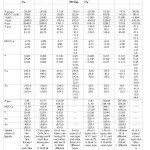Table4: ESR and NMR Parameters of Cu (II), N and X (Cl, Br, I, NCS)  Click here to View table

 

Number of ESR Peaks in [Cu (deta) Cl2]

In [Cu (deta) Cl2], the relative order of A ten values was observed as:

Two types of the three N › First Cl › Cu (II)› Second Cl

The two types of the three N gave 15 lines (b) with each line splitting into a quartet from first Cl to give 15 quartets. Each line of these quartets again split into another quartet from Cu (II)whose each line would further split into another quartet from the second Cl.

Number of ESR Peaks in [Cu (deta) Br2]

In [Cu (deta) Br2], the relative order of A ten values was:

One Br › Two types of the three N › Second Br› Cu(II)

One Br gave a quartet with each line splitting into15 linesfrom two types of three N (b) to give 15 quartets. Each line of these quartets split into another quartet from the other Br to give sixty quartets. Each line of these quartets again split into a quartet from Cu(II).

Number of ESR Peaks in [Cu (deta) I2]

In [Cu (deta) I2], the relative order of A ten values was:

Both I › Two types of the three N › Cu (II)

Two non equivalents I gave 36 lines (c) with each line splitting into 15 lines from two types of three non equivalentsN;with each line further splitting into a quartet from Cu(II).

Number of ESR Peaks in [Cu (d e t a) (NCS) 2]

In [Cu (d e t a) (NCS) 2], the relative order of A ten values was given as:

Cu (II) ›Four types five N; two of one type and remaining three of three different types. Here, Cu (II) gave a quartet with each line splitting into 135 lines from two types of a total of five N [(2.2.1+1) (2.1+1)3](b , c,) .

Table for ESR and NMR Parameters of Cu (II), N and X (Cl, Br, I, NCS) of [Cu (tpy) X2] Complexes

Table: 4 contained A ten, NQCC, , σ, δ values of the parameters of Cu(II) and the CA of complexes [Cu (tpy) X2] (X= Cl, Br, I, NCS) with X=Cl, Br having symmetry symbols (C2v) while the complexes (X=I, NCS) possessed C1 and Cs symbols respectively. Their ESR discussion is divided into four parts:

Number of ESR Peaks in [Cu (t py) Cl2]

In [Cu (t py) Cl2] the relative order of Aten values was:

Two types of the three N› Cu(II)› Both the Cl

Two types of the three N gave15 lines (b);each line splitting into a quartet from Cu (II) to give 15 quartets. Each line would again split into a septet from two equivalents Cl.

Number of ESR Peaks in [Cu (t py) Br2]

In [Cu (t p y) Br2], the observed relative order of A ten values was:

Two Br › Two N of same type › Cu (II)› Third N of different type

Both the equivalents Br would give a septet (a) with each line split into a quintet from two equivalents N to give 35 lines (b). Then each line split into a quartet from Cu (II) whose each line would further split into a triplet from the third N.

Number of ESR Peaks in [Cu (t py) I2]

In [Cu (t p y) I2], the relative order of A ten values was observed to be:

Both I of two different types› Cu (II) › Three N of three different types

The two non equivalents I would give 36 lines (c) with each line splitting into a quartet from Cu(II).Then, each line should split into 27 lines from three non equivalents N.

Number of ESR Peaks in [Cu (t p y) (NCS) 2]

In [Cu (t p y) (NCS) 2], the relative order of A ten values was:

Two N of same type › Cu(II)› Three N of three different types

Two spatially equivalents N gave a quintet (a) with each line splitting into a quartet from Cu(II). Then each line again would split into 27 lines (c) from three spatially different N.

Conclusion

The originality, the relevance, the objective of present work and how it moved the body of scientific knowledge forward would lay in the fact that we were able to theoretically predict the number of ESR peaks even in these highly distortedcopper (II)complexes.

Acknowledgement

Authors, gratefully, acknowledge the kind and willing cooperation of Mr. Sunil Chawla [sunil@seascapelearning.com] of ADF (http://www.scm.com).They feel indebted to Mr. S.R. Heer , Chief Engineer (Retd.), North Zone, Doordarshan, New Delhi (India), for his invaluable cooperation in the smooth working of the ADF software.

References

1. Atanasov, M.; Daul,C. A.;Rauzy,C.; Chem. Phys. Lett. 2003, 367, 737-46.
2. Atanasov, M.; Daul, C.; Güdel, H. U.; Wesolowski,T.;Zbiri, M.; Inorg. Chem. 2005, 44, 2954-63
3. Atanasov,M.; St. Nikolov, G.; Proc.10th Conference, CSSR, 4-7.06., 1985, 11-16.
4. St. Nikolov, G.;Atanasov,M.;Inorg. Chim.Acta. 1983, 72, 95-101.
5. Atanasov, M.; St. Nikolov, G.; Chem. Bulg. Acad. Sci. 1983, 16, 329-36.
6. Atanasov, M.; PhD Thesis, Bulgarian Academy of Sciences, Sofia, Bulgaria, 1983
7. Venter, M.; Haiduc, I.; David, L.; Cozar,O.; J.Mol.Str. 1997, 408–409, 483-86.
8. Kutoglu, A.; Allmann, R.; Folgado, J. V.; Atanasov, M.;Reinen,D.;Z.Naturforsch, 1991, 46b, 1193-99.
9. Dotson, R. L.; Inorg. &Nucl. Chem. Lett. 1973, 2, 215-25.
10. Reinen, D.; Atanasov, M.; St. Nikolov, G.; Steffens, F.; Inorg. Chem. 1988, 27, 1678-86.
11. Atanasov, M.; Kesper, U.; Ramakrishna, B. L.; Reinen, D.; J. Solid St. Chem. 105, 1993, 1-18.
12. Lanthe, van.;vanderAroird,E .; Wormer, P. E. S.; J. Chem. Phys. 1997, 107, 2488-98.
13. Lanthe, van.;vanderAroird, E.;Wormer, P. E. S.; J. Chem. Phys.1998, 107, 783-96.
14. Lanthe, van.;Baerends, E. J.;J. Chem. Phys. 2000, 108, 8279-92.
15. Kaup, M.;Buhl, M.;Malkin, V. G.; ed. Wieley-VCH- Weimheim, 2004.
16. Chikate, R. C.;Padhye, S. B.;Polyhedron 2005, 24(13), 1689-1700.
17. Atanasov, M.; Daul, C. A.;Fowe, E. P.; Chemical Bonding in Molecules and Complexes Containing d-Elements,2005, 136, 925-63.
18. Louati, A.;Kuncaka, A.;Gross, M.; Haubtmann, C.;Bernard, M.;André, J. J.; Brunette, J. P.; Organometallic Chemistry, 1995, 486, 95-104.
19. Ballhausen, C.J.;Molecular Electronic Structures of Transition Metal Complexes, Mc Gray -Hill, London, 1979.
20. Pyykko, P.;Theory and Applications p.7-19 Wiley-VCH, Weinheim, 2004.
21. De Brouchere. G.;Adv. Chem. Phys. 1978, 37, 203-304.
22. Dordrecht K.;Nuclear Magnetic Shielding and Molecular Structure, Ed. Tossel, J.A., 1993.
23. Bieger, W.;Seifert, G.;Eschrig, H.;Rossmann, G.;Chem. Phys. Lett. 1985, 115, 275.
24. Freier, D. G.;Fenske,R. F.; Zheng, X.;J .Chem. Phys. 1985, 83, 3526-37.
25. Malkin, V. G.;Zhidomirov, G. M.;Kim. Z. S. 1988, 29, 32-36.
26. Malkin, V. G.;Malkina, O. L.;Salahub,D. R.; Chem. Phys. Lett.1985, 115, 87-95.
27. Malkin, V. G.;Malkina,O. L.;Salahub, D. R.;Chem. Phys. Lett.1985, 115, 80-86.
28. Arduengo, A. J.;Dixon, D. A.;Kumashero,K. K.; Lee, C.; Power, W. P.;Zilm, K.W.; J. Am. Chem.Soc.1994, 116, 361-67.
29. Schreekenbatch,G.;Zieglar, J. T.;Phys. Chem. 1995, 99, 606-10.
30. Rauhut,G.;Puyear, S.;Wolinski,K.;Pilay, P.;J. Phys. Chem.1996, 100, 6310-16.
31. Cheeseman, J. R.;Trucks, J. W.;Keith, T. A.; Frisch, M. J.;J. Chem. Phys.1996, 104, 5497-5509.
32. Malkin, V.G.;Malkina, O. L.;Salahub, D. R.;Chem. Phys. Lett. 1994, 221, 91-99.
33. Dixon, R. M.;Zieglar, T.; J. Phys. Chem.1996, 100, 5286-90.
34. Autschbach, J.;Zieglar, T.; J. Chem. Phys. 2000, 113, 936-947.
35. Helgaker, T.;Watson, M.;Handy, N. C.;J. Chem. Phys. 2000, 113, 9402-09.
36. Sychrovsky, V.;Grafenstein, J.;Cremer, D.;J. Chem. Phys. 2000, 113, 3530-47.
37. Pederson, M. R.;Khanna, S.N.;Phys. Rev. B. 1999, 60, 9566.
38. Neese, F.; J. Chem. Phys. 2007, 127, 164112.
39. Van W”ullen, C.; J. Chem. Phys.2009, 130, 194109.
40. Schmitt, S.;Jost, P.;van W”ullen, C.;J. Chem. Phys.2011, 134, 194113.
41. Schreckenbach, G.;Ziegler, T.;Int. J. Quantum Chem. 1997, 61, 899.
42. Wolff, S. K.;Ziegler, T.;J. Chem. Phys. 1998, 109, 895.
43. Baerends, E. J.;Branchadell, V.;Sodupe,M.; Chem. Phys. Lett. 1997, 265, 481.
44. Lipkowitz, K. B.;Boyd,D. B.; Rev. Comput. Chem. 2000, 15, 1-86.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.