Degree distance and reverse degree distance of one tetragonal carbon nanocones

Introduction

A molecular graph is  a  simple graph such that its vertices correspond to  the  atoms and the edges to the bonds. A path of a length  n in a graph  G  is  a  sequence of  n+1 vertices such that from each of these vertices there is an  edge  to  the next vertex in the sequence. Let G be a  molecular graph, with the vertex and edge sets of which are represented by V(G) and E(G), respectively. The  distance , d(u,v) is defined  as  the  length  of  the  shortest  path  between u and  in G.  D(u) denotes  the  sum  of  distances between  and all other vertices of G. For a  given  vertex  u of V(G) its  eccentricity, ecc(u) is the largest distance between  and any other vertex v of G.

Table1: Types of vertices of C[n]  Click here to View table

 

The maximum eccentricity over all vertices G of is called the diameter of G and denoted by Diam(G) and the minimum  eccentricity  among  the  vertices  of G is  called  radius of and denoted by R(G) .

[Table2: Categorization of vertices of C[n   Click here to View table

 

Research  into carbon  nanocones (CNC) started  almost  at  the same  time  as  the discovery  of  carbon nanotubes (CNT) in 1991. Ball   studied the closure of (CNT) and mentioned  that (CNT) could  sealed  by a conical cap (1). The  official  report  of the discovery of isolated CNC was  made in , when Ge and Sattler reported their observations  of carbon nanocones  mixed   together   with   tubules  and  a  flat  graphite surface  (2). These  are constructed  from  a graphene sheet by removing a 120⁰ wedge  and  joining  the edges  produces  a cone with a single tetragonal defect at the apex.

Topological indices are graph invariants and  are  used for Quantitives  Structure-Activity Relationship (QSAR) and  Quantitives Structure-Property   Relationship  (QSPR ) studies  (3,4).  The  Wiener  index  of  a graph G denoted by W(G)  is defined W(G) = 1/2 Σ_vεV(G) D(u). The  parameter DD(G) is called the degree distance G of  and it was introduced by Dobrynin and Kochetova (5) and Gutman (6) as  a  graph – theoretical  descriptor  for  characterizing  alkanes;  it  can   be considered as a weighted version of the Wiener index. It is defined as

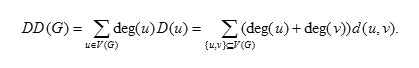
When G is a tree  on n vertices, it has been demonstrated  the Wiener index and degree distance are closely related by DD(G) = 4W(G) – n  (n-1). The reverse degree distance of the graph G is defined as ” DD(G) = 2q (p-1) Diam(G) – DD(G), where p,q are  the  number  of  vertices  and  the  number  of  edges  of G, respectively. Some properties of  the reverse degree distance, especially for trees, have been given in (7, 8). There are two reasons for the study of this graph invariant. One is that the reverse degree distance itself is a topological index  satisfying  the  basic  requirement  to  be  a  branching index and with potential for application  in  chemistry  (8). The  other  is  the  study of  the reverse  degree distance is actually the study of the degree distance, which is important in both mathematical chemistry and in discrete mathematics.

In this paper, we calculate the degree distance and reverse degree distance of one tetragonal carbon   nanocones  CNC₄ [n].

Results and Discussion

The  aim  of  this  section  is  to  comput the degree distance and reverse degree distance  of  one tetragonal carbon nanocones (C[n] = CNC₄ [n]). To do this, the following lemmas are necessary.

Lemna 2.1 |V(C[n])| = 4(n+1)^2_, |E (C[n]) = 6n² + 10n+4.

Proof.  It is clear

       In the following lemma, the diameter and radius of this  nanocone  are computed

Lemma 2.2 R (C[n]) = 2n+2 and Diam (C[n]) = 4n+ 2.

Proof.  It is clear

The Lemma 2.2  shows  that  eccentricities of vertices of C[n] are veried  between  2n+2 and 4n+2. Furthermore,  we observe that there are two   types   of  vertices  in C[n]. 4n² internal  vertices  of  degree    have eccentricities  between  2n+2 and 4n and 4n external vertices of degree  and 4n+4 external  vertices  of degree have eccentricities between 3n+2 and 4n+2. Now  we use an algebraic method for computing the degree distance of one  tetragonal carbon nanocones C[n]. when n is odd, the external vertices of C[n] are mad of n+1/2 types of vertices of degree  with  eccentricity  equal  to 3n+2k+2 and n+1/2 types of vertices of degree  with eccentricity equal to 3n+2k+3 for 0 ≤ k ≤ n-1/2.  But  when n is even, the  external vertices  of C[n]  are made of n/2 types of vertices of degree 3 with eccentricity equal to 3n+2k+3 for 0≤ k ≤ n-2/2 and  also n+2/2 types  of  vertices  of  degree  with eccentricity  equal  to 3n+2k+2 for 0≤ k ≤ n/2. from Figure , in  one  eight  of C[n], when 1≤k≤|n/2|+1 there are k numbers of vertices and when |n/2|+2≤k≤n+1, there are n-k+2 numbers  of  vertices  with  eccentricity  equal  to 2n+2k. Similarly, when 1≤k≤n/2, k numbers  and   when |n/2|+1≤k≤n, n-k+1 numbers  of vertices have eccentricity equal to 2n+2k+1, see Table . For computing the degree distance of one tetragonal carbon nanocones, at first we comput distance sum of all vertices.  From Figure  (left to right) if  be  t-th  vertex of G with  eccentricity equal to  then we denote its distance sum by D(u_m^(t)). Distance sum of all vertices of C[n] is computed in  the following lemma.

Lemma 2.3  Distance  sum  of  all  vertices   of  C[n] is  computed  by   two relations as:

 

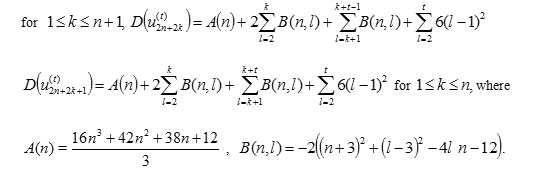
proof. If u be a vertex of central tetragon with eccentricity equal to 2n+2 then  for 1≤k≤2n, 2k+1 numbers  of  vertices  have distances equal to k and also 3n+2 numbers of vertices have distances equal to 2n+1 and n+1 numbers of vertices have distances equal to 2n+2 form u. Thus  

 

Now by using above relations alternatively this proof is completed.

Figure1: The notation of vertices  of C[4] Click here to View figure

 

Figure2: The distance sum of vertices of C[4] Click here to View figure

 

Theorem 2.1 The degree distance of C[n]  is computed as

DD ([n]) = 348/5n⁵ +319n⁴ +572n³ +502n² + 1052/5 n+31,

where n≤1 is an odd number.

Proof. The distance sum of numbers of vertices  is  equals to D (u^(k) 2n+2k), where 1≤k≤n+1/2. Similarly, the distance sum of numbers of vertices  is  equals to D (u^(k) 2n+2k+1) where 1≤k≤n+1/2. Other  vertices  with the same distance sum are eight numbers. All vertices are of degree, except external vertices with eccentricity equal to 4n+2-k,  , where  their degrees are equal to 2, when O≤k≤n-1/2. See Table 2. Thus from Lemma  2.3 we have

 

where n≥2 is and even number.

Proof. The distance sum of numbers of vertices is equals to D(u^(k)2n+2k). where 1≤k≤n+2/2. Similarly, the  distance sum of 4 numbers of vertices is equals to D(u^(k)2n+2k+1), where 1≤k≤n/2. These vertices are on the line L in Figure 2. Other vertices with the same distance sum are eight numbers. All vertices are of of   degree 3 ,  except external vertices with eccentricity equal to 4n+2-k, where their degrees are 2 , when 0≤k≤n/2. See Table 2. Thus from Lemma 2.3 we have

where n≥1 is and odd number.

Proof. It is clear from Lemma 2.1 and Lemma 2.2 and Theorem 2.1.

Theorem 2.4 The  reverse degree distance of

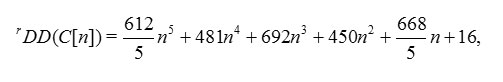
where n≥1 is an even number

Proof. It is clear from Lemma 2.1 and Lemma 2.2 and Theorem 2.2.

Refrences

1. Ball,  P., Needles in a carbon haystack, vol. 354., Nature, (1991).
2. Ge,  M., Sattler,  K., Chem. Phys. Lett. 1994, 220, 192–196.
3. Balaban, A. T., Gordon and Breach   Science   Publishers, The  Netherlands, (1991).
4. Gutman, I., Polansky, O.P., Mathematical Concepts in Organic Chemistry. Springer-Verlag, New York,  (1986) .
5. Dobrynin, A., Kochetova,  A.A.,  J. Chem. Inf. Comput. Sci. 1994, 34, 1082–1086.
6. Gutman, I., J.Chem. Inf. Comput. Sci. 1994, 34, 1087–1089.
7. Tomescu, I., Discrete Math . 1999, 309,  2745–2748.
8. Zhou, B., Trinjistic,  N.,  J. Math. Chem . 2010, 47, 268–275.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.