Quantum mechanical investigation of 2,3-dihydro-1-methyl-2-thioxopyrimidin-4(1H)-one tautomers and their complexes with iodine.

Introduction

Methimazole, carbimazole and propyltiouracilare anti-thyroid drug which depress the formation of thyroid hormones by inhibiting the first step of the hormonal biosynthesis which is the incorporation of oxidized iodine into tyrosine residues in the large thyroid hormone precursor molecule, thyroglobulin [1-4].Pyrimidinderivates too, are known as iodine absorbent in a human body [5-10]. Each compound with a powerful complex with iodine can be considered as a new drug [3], generally, treatment of perthyroidism is achieved by two different mechanisms.

One mechanism is the coordination to iodine and the prevention of electrophilic substitution of iodine on tyrosine [11-18] and another is the coordination to a metal ionic center of tyrosineperoxide and its deactivation [19].The first mechanism was considered in this study.Therefore, we decided to design new molecules with high ability to complex with iodine, which can be used as a new drug for hyper thyroidism.

In the present work, we used computational method to investigate tautomerism and the stability of 2,3-dihydro-1-methyl-2-thioxopyrimidin-4(1H)-one  complexes in the gas phase.Another important aspect of this molecule is its diversity in tautomerism [20,21].

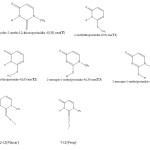Scheme 1  Click here to View scheme

 

g.1.possible  tautomers and numbering  schem  for T and  structuers of complexes.

Table1. Molecular Parameters for the Complexes and the most Stable Isomer of each Tautomer.

Molecules	T	T1	T2	T3	T4
C3-S	1.669	1.771	1.772	1.793	1.791
C3-N2	1.385	1.304	1.307	1.381	1.386
C3-N4	1.375	1.366	1.363	1.291	1.289
C-O	1.223	1.225	1.226	1.225	1.224
N2-c3-N4	114.4	123.1	122.9	125.3	125
S-c3-N4	121.9	115.1	121.3	119.3	114.2
C1-N2-c3	121.1	116.2	116.4	116.7	116.3
C5-N4-C3	128.8	123.9	123.9	120.71	121.2
N2-C1-C5-N4	0.0	0.0	0.0	0.0	0.6
Complexes	T	T-T2(perp)	I-I2(planar)
C3-S	1.669	1.689	1.690
S-I	–	3.147	3.045
I-I	2.660	2.776	2.791
C3-N2	1.385	1.373	1.377
C3-N4	1.374	1.364	1.361
C-O	1.223	1.220	1.219
N-H	1.014	1.015	1.022
NH-I	–	–	2.691
N2-C3-N4	114.3	115.4	115.7
S-C3-N4	121.8	120.9	122.5
I-S-C3	–	90.4	101.7
C1-N2-C3	121.0	120.6	120.6
C5-N4-C3	128.7	128.3	127.8
I-S-C3-N4	–	104.7	0.0
N2-C1-C5-N4	0.0	0.0	0.0
I-I-S-C3	–	-14.9	0.0

 

This molecule has different tautomers, and  two complexes with iodine(fig1).

A study of tautomerism, especially in biologically active molecules, has been one of the most interesting in computational researches because tautomerism plays an important role in the determination of compound application [22-34], and different tautomers of each molecule behave differently in both chemical and biological systems. Thus, since the biological, chemical, and complexation properties of T are different in different tautomers, we have attempted a thorough analysis of this molecule in both the tautomery scheme and complexation properties in our study.

In this research, molecular parameters (Table 1), relative energie (Table 2), of T tautomers were calculated using B3LYP/6-311++G^** and B3LYP/6-31+G^**levels of theory to study its tautomery scheme and properties of all tautomers.

In addition, NBO calculations were made to obtain natural atomic charges (Table 4). Occupation numbers (Table 5), and acceptor_donorinteraction (Table 6,7)of all tautomers and complexes using the B3LYP/6-311++g^**level of theory then, AIM analyses (Table 8) of the complexes were performed to determine the complexation properties of different tautomers in the interaction with iodine. Computation details and the result obtained in this work are presented below.

Methods

Density functional theory (DFT) has been widely applied by chemists to study the electronic structure of molecule in the past year [35,36]. In this work, all calculation were carried out using Becke’ s three parameter density functional [37] and Lee, Yang, and Parr functional [Table 13] to describe gradient-corrected correlation effects, which leads to the well-known B3LYP method.The B3lyp method has been validated to give result similar to those of the more computationally expensive MP2 theory for molecular geometry and frequency calculation(39-41).The geometry optimizations were performed for all tautomers by the B3LYP method with 6-31++G^**and 6-31++G^** basis sets. And the NBO analysis [42] was carried out at the B3LYP/6-31++G^** level of theory. All optimizations and NBO analysis was carried out using the Gaussion03 program package [43]. AIM analyses were performed using the AIM 2000 program [44]. This method has presented useful information about inter molecular interactions and the characterization of bonds through the analysis of the electron density [45].

Result and Discussion

All geometries of T were optimized with the B3LYP methods as a part of the Gaussian 03 [3 ]. A theorical rational method cannot presently be reached for complexes with so many electrons. Therefore, for T-I₂ complex we used DFT methods with two basis sets.

As it can be seen from the calculated Gibbs free energy values listed in Table (1 ), the B3LYP methods all suggest that thionetautomer T is more stable than the thiol tautomer in the gas phase. By observing Table 1, important aspect of the molecular structure can be followed. The C₃-S bond lengths are listed in the first row. The value of this bond length in T is 1.672 A^ᵒ and 1.693-1.696 Aᵒ in their complexes.

The difference between the C = S bond length in complexes  and monomer can result interactions between anti-bonding orbital Lone pair of sulfur and iodine. In the presence interaction ,the charge-transfer of the ring nitrogen atom to  sulfur increases  and the C = S bond length decreases  relative to the monomer.

In next rows, S-I and I-I bond length of the complexes are listed. The S-I bond is slightly shorter in the planar complexes than that in the perpendicular complexes, but any important difference does not exist between different complexes in I-I bond lengths.

Next 4 rows of table 1 consist of bond angles. Observing bond angle variation, we can follow hybridization changes in the central action of each angle. For example, when the central atom is SP², its angle is near 120 degree (as C₃ in all tautomers and N₄ in T₂ and T₄).

But for C₃, the exocyclic angle (N₂-C₃-N₄) is smaller than the exocyclic angle (S-C₃-N₄) because of a higher mobility of the external sulfur atom.

Dihedral angles are listed in the last columns of table 1. The value of the N₂-C₁-C₅-N₄ dihedral angle can show the degree of planarity of the molecules. This value is near zero in all tautomers and complexes, so that these values confirm the planarity of all structures.

Moreover, the I-I-S-C₃ and I-S-C₃-N₄ dihedral angles determine the situation of the iodine molecule versus tautomers.

Table2: Relative Enthalpies and Gibbs Free Energies of All Tautomers and Complexes Versus the Most Stable Structuer(kcal/mol)

Tautomers	B3LYP/6-31+G**			B3LYP/6-31++G**			Complexes	B3LYP/6-31+G**			B3LYP/6-31++G**
	ΔZPE	ΔH	ΔG	ΔZPE	ΔH	ΔG		ΔZPE	ΔH	ΔG	ΔZPE	ΔH	ΔG
T	0	0	0	0	0	0	T-I2 (planar)	1.83	-36.17	-0.68	1.81	-37.85	-2.03
T1	-6.11	11.58	7.82	-6.10	11.72	7.90
T2	-6.02	24.12	21.37	-6.07	24.12	21.33
							T-I2 (perp)	1.65	-29.25	3.89	1.51	-32.82	1.20
T3	-11.10	65.82	62.78	-11.15	65.77	62.63
T4	-11.89	84.66	80.41	-11.73	84.55	70.78

 

Energies

The relative zero point energies, enthalpies, and Gibbs free energies for the most stable tautomers and isomers. T has the lowest enthalpy and Gibbs free energy at both levels of theory. T has both C=S and C=O strong double bonds, so these strong bonds can be responsible for the most stability of this tautomer. The some observation about the relative stability of cyclic tautomers was observed in various pyrimidine and purine bases [47-49].

The relative stability of other tautomers and geometric isomers obtained at the B3LYP/6-31++G^** Level of theory is found to be as follows: T> T₁>T₂>T₃>T₄.

Moreover, the relative stability of the complexes is found to be as follows: T-I₂ (planar)>T-I₂ (perp).The data in the table( 2) show that ΔG for formation complex (T-I2) planer  by 10.7 kJ/ mol lower than another T-I2 complex . The equilibrium constant of the complex formed  T-I2 planar  is more than T-I2 perpendicular.  Enthalpy and entropy reduced with formation complex. The reduction in the enthalpy of the complex plane is more the complex perpendicular.

Table 3.The Calculated Nh Stretching Wave Numbers(Cm^-1) of the T and Complexes

Method	T	T-I2(Planar)	T-I2(perp)
B3LYP/6-31+G(d, p)	3597.28	3444.35	3589.58
B3LYP/6-31++G(d, p)	3597.68	3444.7	3589.9

 

In order to support this hypothesis, we have calculated the NH stretching wave number of the T and T–I2 complexes.The NH stretching wave numbers of the T and T–I2 complexes as computed at B3LYP/6-31++G** and B3LYP/6-31++G* (3-21 G** for iodine atom) level of theory, are reported in Table 3. The comparison of the calculated vibrational wave number of N–H bond of the T compound (3633.22 cm^-1) with the planar form of T–I2 complex (3404.16 cm^-1) reveals that the N–H stretching vibration Vs undergoes a substantial shift towards a lower wave number in agreement with the IR spectrum.Thus, the lengthening of the covalent N–H bond can be considered as a test for the presence of a hydrogen bond.This interaction brings an additional stability to the planar form of the T–I2 complex.

Table 4.Natural atomic charge (in atomic units,au) extracted from NBO calculations

Molecules	C3	N2	N4	O8	S6	CH3	C5
T	0.2438	-0.4392	-0.6342	-0.5968	-0.1682	0.2899	0.6419
T1	0.2934	-0.5553	-0.6303	-0.6180	0.2934	-0.0208	0.6295
T2	0.2872	-0.5342	-0.6330	-0.6216	0.3395	-0.0725	-0.6279
T3	0.3192	-0.4335	-0.5411	-0.5877	0.0264	0.2768	0.6079
T4	0.3067	-0.4507	-0.5413	-0.5854	0.0954	0.2701	0.6082
COMPLEXES	C3	N2	N4	O6	S	I15	I16
T-I2(planar)	0.2692	-0.4137	-6164	-0.5073	-0.1085	-0.0110	-0.1473
T-I2(perp)	0.2730	-0.4114	-0.6098	-0.4862	-0.1612	-0.0217	-0.1273

 

NBO Analysis

NBO population analyses were made to obtain natural atomic changes and the other important complexation properties. Table 4 present the natural atomic of atoms in all isomers and complexes. The numbering scheme of this table is the same as the scheme presented in fig .1.

In tautomers (T,T₁,T₂,T₃,T₄), all nitrogen and oxygen atoms have negative charges and carbon and hydrogen atoms have positive charges. These charges are usual, however, interesting charges were observed in the sulfur atom. In T and complex sulfur has a negative charge, while in the other tautomers it has a positive charge because in T, the sulfur atom is bound only to C₃ with a double bond while in the others, sulfur is bond to two atoms by single bonds. Other atomic charges of the atoms in tautomers have usual values with a little variation between the tautomers. In the complexes, the sum of net charges of all atoms in larger in the tautomer than those in simple tautomers, because negative charges are placed on the iodine atoms. These charges provide another proof for the existence of a real complex between the tautomers and iodine. Also, in the planar complex, the absolute values of charges placed on the iodine atoms are larger than perpendicular complex. This shows that a more effective interaction (between the tautomer and iodine) seems to exist in the planar complex.

One of the important results obtained from NBO calculations is orbital occupancies and another is acceptor-donor interactions. In table 5, selected occupation numbers for all tautomers and complexes are listed. The occupancies given show that most bounding orbitals and lone pair consist of more than 1.9 electrons, but some lone pairs have occupation numbers between 1.6 and 1.98.

these occupancies display that important donor properties can exist on these lone pairs. Also, a significant change in the occupancies of the δ or π bond between the tautomers and complexes has not been observed.

Table 5. Most important occupancies of NBO in atomic units

	T	T1	T2	T3	T4	T-I2(planar)	T-I2( PERP)
δC3-S6	1.9824	1.9774	1.9769	1.9792	1.9784	1.9885	1.9850
πC3-S6	1.9809	–	–	–	–	1.9851	1.8675
LP1N2	1.5796	1.8968	1.8954	1.5993	1.6034	1.5586	1.5455
LP1N4	1.6030	1.6913	1.6002	1.8866	1.8820	1.5610	1.5618
LP1S6	1.9854	1.9856	1.9804	1.9868	1.9855	1.9842	1.9859
LP2S6	1.8729	1.8233	1.8204	1.8676	1.8741	1.7193	1.8803
LP1O8	1.9776	1.9771	1.9768	1.9778	1.9780	1.9776	1.9765
LP2O8	1.8605	1.8563	1.8542	1.8692	1.8692	1.8399	1.8366
δ*C5-O8a	0.0094	0.0094	0.0096	0.0154	0.0158	1.9979	1.9982
Π*C5-O8b	0.3120	0.3428	0.3506	0.2974	0.2949	1.9929	1.9938
δ*C3-S6c	1.4709	0.05168	0.0466	0.5369	0.0478	1.9634	–
πC3-S6d	0.0100	–	–	–	–	0.1922	0.1577

 

^aIn complexes; Lp1_I15,^b In complexes; Lp2_I15,^c In complexes; Lp3_I15,^d In complexes: δ*_I15-I16 This observation confirms that the δ Or  π bond do not contribute in electron donation to iodine. On behalf , a significant decrease was observed in the occupation number of lone pair 2 of sulfur in the complexes versus tautomer T, which shows that this lone pair is donated to the iodine atom.The occupation number of π^*C₅-O₈ in the tautomers show that resonance is between the N₄ lone pair and the C₅=O₈ double bond. Otherwise, the N₄ lone pair has resonance with π^*C₅-O₈ The same result were observed in the π^*C₃-S₆ Occupation number in T and another tautomers.

Because of a higher capacity of the sulfur atom in electron acceptance, these occupancies are higher in the previous example.

Table6. acceptor- Donor Interaction Energies (in kcal/mol) in the tautomers and complexes.

Donor	Acceptor	T	T1	T2	T3	T4	T-I2(planar)	T-I2(PERP)
LP1N2	δ*C3-S6	68.70	2.75	2.38	–	–	83.83	85.82
LP1N4	δ*C3-S6	74.14	–	–	3.05	2.94	99.60	94.08
LP1N4	δ*C3-O	–	–	44.77	2.65	2.73	48.76	46.90
LP1N4	π*C3-O	49.02	46.11	–	–	–	–	–
LP1S6	δ*C3-N4	3.38	–	4.99	4.01	–	3.25	1.19
LP2S6	δ*N2-C3	13.55	–	–	–	0.69	12.95	11.76
LP1S6	δ*N2-C3	3.37	5.16		–	4.07	0.51	2.56
LP2S6	π*N2-C3	–	27.28	25.63	–	–	–	–
LP2S6	δ*C3-N4	11.07	–	–	–	0.72	–	–

 

The list of important donor-acceptor interactions is given in table 6. As shown in this table, the lone pairs of N₂, N₄, and S6 are important donors, and C-N, C-S, and C-O bonds are the main acceptors. The most powerful interactions are LP₁N₂ to π^*C₃-S₆ and LP₁N₄ to π^*C₄-O₈, and powerful resonance exists between the nitrogen lone pair and the C=S or C=O double bond. Another important interaction is electron donation by LP₂S₆ to the δ^*C₃-N₄.

This interaction has not been observed in most complexes because of the donation of this lone pair to iodine.It is obvious that in T₁ and T₂, the C₃=N₄ double bond exists. So this interaction is replaced by LP₂S₆ donation to π^*C₃-N₄.In addition, special donor-acceptor interactions were listed only for the complexes in table 7.

Table7. Special Acceptor-donor Interaction Energies (in kcal/mol) in the complex.

Donor	Acceptor	T-I2(Planar)	T-I2(Perp)
LP1S6	δ*I-I	2.36	1.92
LP2S6	δ*(I-I)	28.05	1.12
LP1(I)	δ*(N-H)	0.50	–
LP3(I)	δ*(N-H)	8.48	–

 

The table data listed shows that although both sulfur lone pairs have been in electron donation to iodine, however, one of them (LP₂) is more effective. Moreover in the planar complexes the acceptor-donor energy is significantly higher than in the perpendicular complex in both interactions (LP₁ and LP₂ to δ^*I-I).

This observation confirms our previous estimate about higher efficiency .

Table8. Calculated critical point properties of the complexes.

Complex	r,Aᵒ	P(r),au	▼2p(r),au	CP,A	CP,B	ε	r,Aᵒ	P(r)	▼2p(r),au	CP-A	CP-B	ε
T-I2(planar)	3.07	0.0261	0.0594	1.568	1.4779	0.008	1.690	0.1987	0.4033	1.1002	0.6168	0.007
T-I2(perp)	3.51	0.0211	0.0496	1.604	1.5420	0.165	1.689	0.1973	0.4292	1.0730	0.6166	0.010

←      S-I interaction           →        ←     C-S interaction       →

AIM results. In the final part of our study, AIM analyses performed for the complexes to obtain important complexation properties, and the results are listed in table 8.

The first column consists of S-I interaction data.In this part, P (electron destiny) and this Laplacian may be very useful parameters to estimate the strengths of the S-I interaction.

The low values for the change destiny reflect the weak character of this bond in our complexes.

It is noticeable that the planar complex has the larger value than perp complex of the electron density, confirming the higher efficiency of the planar complex. The negative values for the laplacian of the C-S bond show the covalent bond.

Conclusions

In this report2,3-dihydro-1-methyl-2-thioxopyrimidin-4(1H)-one and their tautomers have been studies to find new structures with the effective ability to make a complex with iodine (for treatment of hyperthyroidism).

All structures and their complex with iodine have been optimized using the B3LYP method with 6-31+G^**and 6-31++G^** Basis sets  (for Iodine 3-21 G**)to obtain their molecular parameters and relative energies.The relative stability of the complexes is found to be:T>T1> T2> T3> T4

The optimized structures show that T menomer make planar complex and perpendicular complex with iodine.The relative stability of the complexes is found to be:

T-I₂ (planar)>T-I₂ (perp). Then, NBO calculations were performed for the tautomers and complexes to obtain atomic charges, occupation numbers, and acceptor-donor interactions. These results confirm the ability of (T) tautomers to form complexes and show that the planar complexes have more effetely interaction than the perp complex. Finally the AIM analyses performed to prove them and obtain complexation properties.

This calculation of the T with iodine is more powerful in the planar complex versus the perpendicular complex.

Refrences

1. Roohi, H.;Ebrahimi, A. and Habibi, S. M. Theochem. 2004,710, 77-82.
2. Kohn, H. B; Kohn, A;Steenberg, M. L. and Buckley, J. P.  J. Med. Chem.1977, 20, 58-64 .
3. Tavakol, H; Hadadi,T;Roohi, H.Theochem.2012,53,649-658.
4. Laurence, C;Elghomari, M. J;Lucon, M.J. Chem. Soc. Perkin Trans.1998, 2, 1159-1162 .
5. Laurence, C;Elghomari, M. J; Berthelot, M. J. Chem. Soc. Perkin Trans.1998. 2, 1163-1167 .
6. Papayannis, D. K; Kosmas, A. M. Theochem.2008, 851, 175-179 .
7. Taurog, . A. J. Biochem. Biophys.1996, 24, 330-337 .
8. Raper, E. S; Creighton, J. R;Oughtred, R. E;Nowell, I. W. Acta Cryst.1983, B, 39, 355-361 .
9. Laurence,v;Elghomari, M. J; Lequestel, J. Y;  Berthelot, M.;Mokhisse, R.J. Chem. Soc. Perkin Trans.1998, 2, 1553-1557 .
10. Jemec, B;ActaPathol. Microbiol.Scand. A,1970, 78, 151-155 .
11. Roy, . G;Mugesh, G.J. Chem. Sci.2006, 118, 619-624 .
12. Roy, G;Mugesh, G.J. Inorg. Chem. Acta.2000, 360, 303-308 .
13. Roy, G;Mugesh, G. J. Inorg. Phys. Chem.2006, 1-6 .
14. Kohrle, J.Endor. Rev,2005., 23, 944-948 .
15. Dunford, H. B.Biochem.2006, 445, 199-204.
16. Kohrle, J.Exp. Clin. Endocrinol.1994, 102, 63-67 .
17. Berry, M. J;Banu, L;Larse, P. R. Nature.1991, 349, 348-354 .
18. Bianco, A. C; Salvatore, D;Gereben, B; Berry, M. J; Larsen, P. R. Endocrine Rev.2002, 23, 38-45 .
19. Kohrle, J.Biochimie.1999, 81, 527-534 .
20. Nowac, . M. J. J. Phys. Chem.1990, 94, 7406-7411 .
21. Fu, A. Theochem.2006, 767, 510-513 .
22. Belova, N. V;Oberhammer, H;Girichev, G. V.;Shlykov, S. A. J. Phys. Chem. A.2008, 112, 3209-3216 .
23. Tavakol, H.Theochem.2012, 954, 16-21 ,658.
24. Dobosz, R;Kolehmainen, E;Valkonen, A;Osmiaowski, B;Gawinecki, R.Tetrahedron.2007, 63, 9172-9178 .
25. Tavakol, H. Theochem.2009, 916, 172-179 .
26. Misra, A; Dalai, S.Theochem.2007, 807, 33-37 .
27. TavakolH;Sabzyan, H. J. Phys. Org. Chem.2010, 1771-1776 .
28. Tavakol, H;Arshadi, S. J. Mol. Model.2009, 15, 807-816.
29. Dubonosov, A. D;Minkin, V. I; Bren, V. A;Shepelenko, E. N;Tsukanov, A. V;Starikov, A. G;Borodkin, G. S.Tetrahedron.2008, 64, 3160 .
30. Tavakol, H.  Mol. Simul.2010, 36, 391-402 .
31. Buzykin, B. I;Mronova, E. V;Nabiullin, V. N;Azancheev, N. M;Awakumova, L. V;Rizvanov, I. K;Gubaiduffin, T;Litvinov, I. A;Syakaev, V. V.Russ. J. Gen. Chem.2008, 78, 461-468 .
32. Tavakol, . H. Int. J. Quant. Chem.2010, QUA22847 .
33. Bonacin, . J. A;Melo, D;Toma, H. E.Vib. Spectroscop.2007, 107 .
34. Tavakol, H.Theochem.2010., 956, 97-102 .
35. Bhan, A; Joshi, Y. V;Delgass, W. N; Thomson, K. T. J. Phys. Chem. B.2003, 107, 10476-10484.
36. Rozanska, X; Santen, R. A; Demuth, T.;Hutschka, F;Hafner, J. J. Phys. Chem. B.2003, 107, 1309-1312.
37. Becke, A. D. J. Chem. Phys.1993, 98, 5648-5653.
38. Lee, T. C; Yang, W. T; Parr, R. G. Phys. Rev. B.1988, 37, 785-791 .
39. Johnson, B. G; W. Gill, P. M;Pople, J. A.J. Chem. Phys.1993, 98, 5612-5616 .
40. Bauschlicher, C. W; Partridge, H.J. Chem. Phys.1995, 103, 1788-1794 .
41. Lee, . C; Yang,W;RParr, . G. Phys. Rev. B.1988, 37, 785-793 .
42. Reed, A. E; Curtiss, L. A;Weinhold, F.Chem. Rev.1988, 88, 899-903 .
43. Frisch et al, M. J. Gaussian 98 Rev. A.1, Gaussian Inc., Pittsburgh PA 1998.
44. Scott , A. P; Radom, I.J. Phys. Chem. B.1996, 100, 16502-16508 .
45. Bieglerkonig, F;Schonbohm, J.J. Comp. Chem.2002.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.