Primary Protection of Reinforced Concrete against Impact of Carbon Dioxide

Introduction

Mathematical Simulation of Concrete Carbonization

Durability of reinforced concrete within corrosion impact of environment can be conditionally subdivided into two periods (Fig. 1):

Figure1:. Schematic view of damage within steel corrosion in concrete [1]  Click here to View figure

 

However, in fact only the time period as t₁ should be reasonably considered as durability T (before initiation of reinforcement corrosion), that is, the time period t₂, should be neglected, since the error of determination of the time period t₂ can be very high.

Exactly this approach is used by numerous researchers [1,2,4,8], though attempts of more or less reliable determination of the time period t₂ are already under way [12]. Up till now there are no standard procedures of calculation of the time period t₁, which determines the urgent character of investigation into this problem. Indeed, the depth of concrete damage as a function of operation lifetime should serve as a basis for solution adoption both within designing of new projects, and within estimation of existing structures. Since the existence of reinforced concrete is possible only with existence of protective layer a_p and cohesion of reinforcement with concrete, then the most convenient way to determine the time period t₁ by functional dependence of the damage depth L=f(t) upon the condition L <  а_p.

According to SNIP Regulations 2.03.11-85 Protection of Engineering Structures against Corrosion. estimated durability can be implemented by the use of means of primary and secondary protection. The primary protection includes increase in density of concrete and thickness of protective layer, the secondary protection includes application of various coatings and impregnations. However, the means of secondary protection have two drawbacks: high cost (in moderate and high aggressive medium by several times higher than the that of the structure itself); in addition, the secondary protection is not durable and should be renewed every 5…10 years.

It is obvious that the final purpose of development of mathematical model of corrosion L=f(t) is the obtaining of simple equation suitable for engineering calculations. Corrosion of concrete is related with interaction between polymineral cement stone and multi-component ambient medium. However, almost all researchers within development of equation L=f(t) aiming at simplification proceed form the interaction only between  two substances.  Mathematical model of physico-chemical interaction between two substances has long been known: these are differential equations of the second order in partial derivatives, which simultaneously includes diffusion, dissolution and chemical interaction between two components: the component А, which is the ambient medium, and the component В, which is soluble components of cement stone (in the case of corrosion of concrete), with slow or fast reaction rate (Fig. 2; Table 1, Eq. (2)).

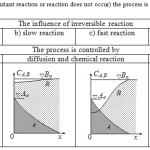Figure2: For most simple cases (instant reaction or reaction does not occur) the process is determined only by diffusion (Fig. 2; Table 1, Eq. (3)).  Click here to View figure

 

Figure2B: Types of curves characterizing the concentration distribution within bimolecular reaction of the following type: А + ВŽ → products [15]Note:  х = х1 — coordinate of reaction plane.  Click here to View figure

 

Until recently the bottleneck of all models was obtaining of simple engineering equation derived from the set (2).   Numerous researchers simplified the equation assuming R_i(c) ~ 0, thus transferring to Eq. (3), also known as the Fick’s second law.  At the same time Eq. (3) has analytical solution in the form of common in the field of concrete durability square–root–of–time law:

where L is the concrete neutralization depth, mm, t is the operation lifetime, years, A is the coefficient depending on the concentration of carbon dioxide c, the effective diffusion coefficient D` and concrete reaction capacity m₀.

Mathematical models, based on these principles and developed by Russian and foreign researchers (S.N. Alekseev [1], V.G., E.A. Guzeev [3], B.V. Gusev [4], T.K. Dement`ev [6], F.M. Ivanov [7], V.M. Moskvin [8], A.F. Polak [8], Sh.M. Rahimbaev [13], N.K. Rozental` [14], V.F. Stepanova [4], A.S. Fai`vusovich [4], V.V. Iakovlev [10], H.I. Wiering [24], V.G. Papadakis [19], M. Liang [18], T. Ishida [17], Younsi [16]), can be finally expressed similar to Eq. (4).

These models were obtained by experimental processing of the results of on-site investigations, laboratory experiments and applied mathematical software. The developed models of the type: L=f(x) can be subdivided into two lines [5]: the first line is applied together with the mass transfer equations for description of kinetics of physico-chemical processes (and is more common); the second line involves dependences of thermodynamic equilibrium.

The drawbacks of the first line consist of mathematical assumptions and simplifications, which influence on the accuracy of calculations. The drawbacks of the second line involve deviations from the results of on-line and laboratory experiments, awkwardness of calculations, numerous coefficients, determination of which requires for development of dedicated procedures.

In general, most cases are reduced to classical solution, known as the already mentioned square–root–of–time law (4).

In Russia the most significant contribution into development of calculation methods of provision of reinforced concrete  durability was made by Prof. A. F. Polak in the 1970s–1980s by means of quasi-stationary mode and subdivision of corroding layer into areas. Despite the fact that the obtained by Prof. Polak equation for determination of the penetration depth of ambient medium into cement stone accounted for numerous process variables, it still remained one of variants of the square–root–of–time law. Mathematical model of the type (4) is based on the solution of differential equations describing various physical and chemical processes of corrosion. However, these solutions were obtained on the basis of several assumptions and this could result in decreased accuracy of the results. One of non-considered in model (4) processes is chemical interaction between ambient medium and soluble components of cement stone, which leads to underestimation of penetration rate of aggressive medium into concrete. Consideration of this process can significantly influence on the type of developed calculation dependence L=f(t) (Fig. 3), which is also mentioned in [13].

Results of Numerical Experiment

We developed and made adjustment of the existing equation of the type (4) by calculation experiment using computer-aided symbolic (analytical) simulation, namely, development of mathematical model based on numerical solution of differential equations combining actually all variables of corrosion (Fig. 3).

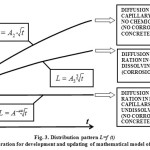Figure3B: Distribution pattern L=f (t) with consideration for development and updating of mathematical model of the process  Click here to View figure

 

The results of numerical experiment make it possible to conclude that within expressed chemical interaction between ambient medium and soluble components of cement stone the mathematical model of concrete corrosion can be as follows:

The obtained calculated data (Table 2) confirm applicability of dependence of the type  L = A₂ √t concretes of high waterproofing with relatively low design or actual operation lifetime. Designing of durability of structures made of concrete brands W6 and higher for long-term operation should be reasonably based on equation  L = A₃ ³√t.

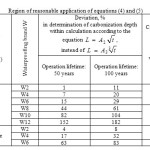Table2: Region of reasonable application of equations (4) and (5)  Click here to View table

 

Based on the data of inspection of technical state of concrete and reinforced concrete structures carried out on several hundreds of facilities with various operation modes the values A_p  were determined (Table 3) as a function of concrete density and temperature–humidity conditions of structure operation, when concrete corrosion occurs under so-called regular conditions of operation and reinforcement corrosion is caused by carbonization of concrete protective layer.

Figure4: Operation lifetime of structure T as a function of waterproofing brand W  under normal operation modes at thickness of protective concrete layer: 1 – ap = 30 mm; 2 – ap = 25 mm; 3 – ap = 20 mm; 4 – ap = 15 mm  Click here to View figure

 

Table 3 Coefficient A_p (cm per year ^-1/3)  as a function of concrete density (W/C) and operation mode of structure 

Water to cement ratio W/C	Waterproofing brand W	Value of Ap
		Normal operation mode	Wet operation mode
0.65	2	1.026	0.51
0.55	4	0.682	0.25
0.5	6	0.51	0.12
0.43	8	0.2692	–
0.4	10	0.166
0.38	12	0.0972
0.35	14	–

 

Conclusions

Therefore, at the stage of designing of structures the obtaining of rated operation lifetime under regular operation conditions (that is, under impact of carbon dioxide and moisture) can be provided only by means of the primary protection – selection of thickness of protective layer a_p, as well as concrete waterproofing brand W (Fig. 4). For instance, at the thickness of protective layer a_p = 30 mm the rated operation lifetime T_r = 100 years can be provided by regular concrete of W4 brand, and if a_p=15 mm, then the rated lifetime T_r =100 years can be achieved without means of secondary protection only by application of concrete of extremely low waterproofing brand of at least W8.

At present the companies of building industry have all the things needed for provision of required concrete brand in terms waterproofing and strict supervision of thickness of concrete layer, thus investors, customers, designers and constructors can be assured of capabilities of implementation of project design concerning achievement of design durability of reinforced concrete structures of various purposes.

Acknowledgments

This work was supported by Ministry of Education of Russia in the scope of Federal program No. 2014/241. Research Project No. 2093.

References

1. S. N. Alekseev, F. M. Ivanov, C. Modry, and P. Shissl. Durability of reinforced concrete in aggressive mediums. Moscow, Stroiizdat, 1990.
2. S. N. Alekseev and N. K. Rozental. Corrosion resistance of reinforced structures in aggressive industrial medium. Moscow, Stroiizdat, 1976.
3. Guzeev E. A., Alekseev S.N., and  Savitskii N. V. Consideration of aggressive impacts in the design regulations for structures. Beton and  Zhelezobeton, 1992, No. 10.
4. B. V. Gusev, A. S. Faivusovich, and V. F. Stepanova, et al. Mathematical models of  corrosion of concrete. Moscow, TIMR Publishing House, 1996.
5. B. V. Gusev and A. S. Faivusovich. Mathematical model of atmospheric corrosion of concretes with consideration for phase transitions. Collection of articles, Analytical solution … PP. 55 – 62
6. Dementiev G. K. Conditions of concrete stability in mineralized waters. Neftianoe hoziaistvo. 1929, No. 9.
7. Ivanov F. M. On simulation of concrete corrosion. Beton i zhelezobeton. 1982, No. 7.
8. Moskvin, V. M. Concrete corrosion. Moscow: State publishing house for construction and architecture, 1952.
9. A. F. Polak, Simulation of corrosion of reinforced concrete and forecasting of its durability. Itogi nauki i tekhniki. Corrosion and protection against corrosion. Vol. XI.  Moscow: VINITI, 1986. PP. 136–180.
10. Polak A. F., Habibullin R. G., Yakovlev V.V., and Latypov V. M. Generalized mathematical model of concrete corrosion in aggressive liquid mediums. Beton i zhelezobeton. 1981, No. 9.
11. Polyanin,  A. D. Guidebook on linear equations of mathematical physics. Moscow: Fizmatlit, 2001.
12. A. A. Prokopovich. Flexural resistance of reinforced structures with various conditions of cohesion of longitudinal reinforcement with concrete.  Samara: NVF. Sensors. Modules. Systems, 2000.
13. Rakhimbaev Sh. M. and Avershina N. M. Forecasting of durability of building materials by single test time. Stroitelnye materialy. 1994, No. 4.
14. N. K. Rozental`. Corrosion resistance of cement blocks of low and extremely low waterproofing. Moscow: Center of Design Products, 2006.
15. Thomas K. Sherwood, Robert L. Pigford, and Charles R. Wilke. Mass transfer, McGraw-Hill Book Company (1975).
16. Younsi, Ph. Turcry, A. Aït-Mokhtar, and S. Staquet. Accelerated carbonation of concrete with high content of mineral additions: Effect of interactions between hydration and drying.
17. T. Ishida, K. Maekawa, and M. Soltani. Theoretically Identified Strong Coupling of Carbonation Rate and Thermodynamic Moisture States in Micropores of Concrete. Journal of Advanced Concrete Technology Vol. 2, No. 2, PP.213-222, June 2004. Copyright © 2004 Japan Concrete Institute
18. Liang, M., Wu, J., and Liang, C. (2001). Multiple Layer Fuzzy Evaluation for Existing Reinforced Concrete Bridges. J. Infrastruct. Syst., 7(4), 144–159.
19. V.G. Papadakis, C.G. Vayenas, and M.N. Fardis, A reaction engineering approach to the problem of concrete carbonation, Journal of the American Institute of Chemical Engineers, 1 (11), 1989, 110-122.
20. Y. Shao, S. Monkman, and A. J. Boyd Recycling carbon dioxide into concrete: a feasibility study / Concrete Sustainability Conference. – National Ready Concrete Association, 2010 – PP. 1-10
21. M.M.Y. Delmi, Étude de l’hydratation et du couplage carbonatationéchanges hydriques dans les mortiers et bétons, Thèse de Doctorat de l’Université de La Rochelle, 2004.
22. History of Cement Static Content [web-resource] / http://www.cement.ca/en/content/History_of_Cement_Static_Content.html
23. International Energy Statistics [web-resource] http://www.eia.gov/cfapps/ipdbproject/iedindex3.cfm?tid=90&pid=44&aid=8 обновл. 11.10.2013
24. Wiering H.J. Longtime Studies on the Carbonation of Concrete under Normal Outdoor Exposure/RILEM – Seminar «Durability of Concrete Structures Under Normal Out­door Conditions», Hannover, 1984, PP.104-108.
25. A. R. Anvarov, P. A. Fedorov, T. V. Latypova, E.V. Lutsyk, T. Z. Gilmutdinov, and V. M. Latypov . Carbonization of concrete:  worried about durability? //The 5th Asia Conference on Earthquake Engineering(5ACEE),  October 16-18, 2014, Taipei, Taiwan

---

This work is licensed under a Creative Commons Attribution 4.0 International License.