Categorization and Structual Determination of Simple and More Complex Carbonyl Clusters of Rhenium and Osmium Using K-Values and the Cluster Table
Enos Masheija Kiremire*
Department of Chemistry and Biochemistry, University of Namibia, Private Bag 13301, Windhoek, Namibia
DOI : http://dx.doi.org/10.13005/ojc/310133
Article Received on :
Article Accepted on :
Article Published : 23 Mar 2015
The shapes of conventional covalent compounds of main group elements and transition metal complexes can usually be deduced from their formulas. However, this is not the case for transition metal carbonyl clusters whose structures more or less resemble those of boranes and carboranes. Tremendous interest in the shapes of metal carbonyl clusters have been kept alive for more than five decades. Polyhedral skeletal theory, Jemmis rules, graph theory, and topological theory among others have been put forward so as to understand the structures of transition metal carbonyl clusters. This paper presents a highly simplified user friendly cluster table based on k-values which can be utilized together with an empirical formula to deduce the symmetries of simple to more complex cluster carbonyl complexes without any background of cluster theories. This approach highly complements the existing theories, in particular, the renowned polyhedral skeletal electron pair theory (PSEPT).
KEYWORDS:shapes; Categorization; Categorization; Carbonyl Clusters
Download this article as:| Copy the following to cite this article: Kiremire E. M. Categorization and Structual Determination of Simple and More Complex Carbonyl Clusters of Rhenium and Osmium Using K-Values and the Cluster Table. Orient J Chem 2015;31(1). |
| Copy the following to cite this URL: Kiremire E. M. Categorization and Structual Determination of Simple and More Complex Carbonyl Clusters of Rhenium and Osmium Using K-Values and the Cluster Table. Orient J Chem 2015;31(1). Available from: http://www.orientjchem.org/?p=8055 |
Introduction
Recently, a cluster table for transition metal carbonyls and has been designed to assist in the categorization of clusters and tentative assignment of geometries of clusters1-5. The cluster table has been re-arranged in such way that it has become much more user friendly. In this way, a given cluster can easily be categorized and its geometry tentatively assigned.
The cluster number, k-value for a carbonyl cluster is calculated1-5 using the empirical formula k = ½ (E-V). By analyzing the cluster numbers, it has been possible to discern the latent infinite world of series of clusters for elements which obey the 18-electron rule or 8-electron rule(octet rule). Some of these series have been organized and are presented in Table 1. In the newly reorganized and simplified table, the columns represent Mx values where x = 2,3, 4, 5, 6, and so on. In this new table,the movement down an Mx column is like driving along a ‘highway’. The movement crosses the columns of different cluster series that vary by ∆k = ± 1.That is, a change of one linkage or bond while the number of skeletal atoms remains the same. It is similar to adding or removing a monodentatelig and (a pair of electrons) step by step. The horizontal movement along the series represents a progressive change in ∆k = ±2 and a change of Mx value by 1. The series comprises of different cluster values( k values) but belong to the same broad category type such as closo, nidoor arachno and so on. In a way each box or square in Table 1 may be regarded to be similar to a ‘clan’ which has many ‘family’ member series. Thus, the box can represent members from, rhenium, ruthenium or osmium ‘families’or any other family and so on. The diagonal movement represent a process in which there is a progressive change by ∆k = ± 3 and Mx by 1 as you shift from one type of ‘cluster clan’series to another. This corresponds to a capping process.
Results and Discussion
A selected range of carbonyl clusters taken mainly from rhenium element have been used as illustrations to categorize the clusters. The results re given in Table 2.In almost all cases categorization of clusters using the empirically calculated k-value and the cluster Table 1 are in agreement with those obtained by the known methods. A few examples are hereby given to illustrate the ease of utilizing the cluster table for categorizing a given cluster from its molecular formula.
- Re4(H)4(CO)132-; E = 4X18 = 72, V = 7×4 +4+ 13×2+2 = 60; k = ½ (E-V) = ½ (72-60) = 6.
‘Raw code’ of the cluster is represented as M-4-6-60:- where M refers to the cluster skeletal element, 4 –the number of skeletal elements, 6-the number of skeletal bonds or linkages, and 60 the total number of valence electrons. Table 1 has been constructed using a series of raw codes. In order to determine the type of cluster series it belongs to, we look at the cluster Table 1 under ‘M-4 highway’. The M-4 highway is scanned until the raw code M-4-6-60 is found. Keeping on the same row, moving to the left, it is found that the raw code is in line with letter N(N = nido). Hence, the cluster is categorized as M-4-6-60-N. Therefore the cluster, Re4(H)4(CO)132- is a member of Nidoclan series of 4 skeletal elements with a total of 60 electrons.The 4 skeletal atoms with 6 linkages are normally found to form an ‘ideal’ tetrahedral (Td ) geometry Fig.1.
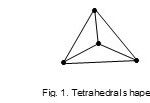 |
Figure 1 Click here to View figure |
The shape is drawn as a projection looking at it from above.
2. Re5(C)(CO)16(H)2-; E = 90, V = 74, k = ½ (E-V) = ½ ( 90-74) = 8. Raw code = M-5-8-74. As can be seen from Table 1, this cluster also belongs to the Nido family. The cluster category is M-5-8-74-N. The skeletal shape will be a square pyramidC4v. This is shown in Fig. 2.
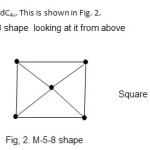 |
Figure 2 Click here to View figure |
3. Re4(CO)162-; E = 72, V = 62, k = 5, raw code = M-4-5-62. Reading from M-4 highway column in table 1, the category code is M-4-5-62-A(arachno, butterfly shape). This shape is given in Fig. 3.
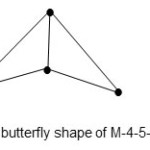 |
Figure 3 Click here to View figure |
4. Os5(CO)16; The cluster has the derived category code of M-5-9-72-C. The complex belongs to the closo series. This is a geometry characteristic of regular trigonalbipyramid(D3h) shown in Fig. 4.
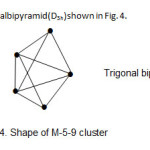 |
Figure 4 Click here to View figure |
5. It is interesting to note6 that the cluster complexex RuIr4(CO)152―(M-5-7-76-A), was found to have elongated trigonalbipyramid shape while on the other hand Os5(CO)16(M-5-9-72-C) was found to have regular trigonalbipyramid shape. The skeletal cluster shape of M-5-7 may be represented as indicated in Fig. 5.
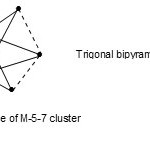 |
Figure 5 Click here to View figure |
It is not a surprise therefore that the two complexes (M-5-7-76-A) and (M-5-9-72-C) differ in length measurements as they truly belong to different series.
K-Isomerism
In some cluster systems with the same cluster code may exhibit different shapes which may be regarded as isomers. For instance7, Os6(CO)182―(M-6-11-86-C) with k value of 11 has an octahedral shape,
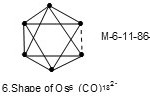 |
Figure 6 Click here to View figure |
while O6(H)2(CO)18 (M-6-11-86-C) with k value of 11 has a mono-capped square pyramid, Fig. 7.
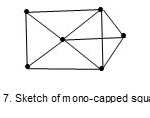 |
Figure 7 Click here to View figure |
Also the complexes7 Re4(H)4(CO)152―(E = 72, V = 64, k = ½ (E-V)= 4;from table cluster belongs to the Hypho series and code is M-4-4-64-H. Similarly, the cluster Re4(H)4(CO)16 has a code M-4-4-64-H. However, the cluster shapes are different. The skeletal shapes are given in Fig. 8 and 9.
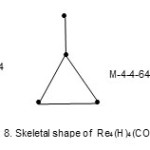 |
Figure 8 Click here to View figure |
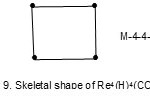 |
Figure 9 Click here to View figure |
More Examples for Illustration of the Use of Cluster Table.
The osmium cluster Os6(CO)18 great interest6. It is considered as a bi-capped tetrahedron or mono-capped trigonalbipyramid. This observation is readily picked out from Table 1. The cluster category code of the complex is M-6-12-84-C1C. As can be seen from the table, it is a mono-cap of M-5-9-72-C (trigonalbipyramid) which is diagonally below it and diagonally below M-5-9-72-C is M-4-6-60-N (a tetrahedral geometry).This capping process is sketched in Fig.
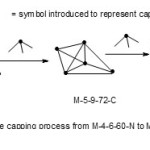 |
Figure 10 Click here to View figure |
Consider the complex Au3Ru4(CO)12L3(H), L = PPh3. It is described as a tri-capped tetrahedron6. Its cluster series category code from the table is M-7-15-96-C2C. Moving along the diagonal in the table, it is observed that it is a bi-cap of M-5-9-72-C(trigonalbipyramid). But M-5-9-72-C is a mono-cap of M-4-6-60-N(tetrahedral). Hence, in essence, it can be regarded as a tri-capped tetrahedron.
Let us take another example8,9, Os6Pt2(CO)6(COD)2, COD= 4-electron donor. It has a cluster category code M-8-18-108-C3C(M-5, difference between 8 and 3). From Table 1, it is a tri-cap based on trigonalbipyramid (M-5-9-72-C) as you move along M-8 diagonal. The skeletal shape of the cluster is is sketched as shown in Fig. 11.
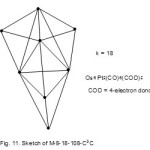 |
Figure 11 Click here to View figure |
The cluster k value can be considered to come from the M-5-9-72-C central unit contributing nine linkages and the three caps donating 3×3 =9 giving a rise of 9+ 9 = 18.
Let us look at another example10, Os7(CO)19Au2(Ph2CH2PPh2). In this case, E = 9×18=162, V=7×8+19×2+4 = 120. Hence, k = ½ (E-V) = ½ (162-120) =21. The corresponding cluster code for this complex will be M-9-21-120-C4C(based on M-5 , specifically M-5-9-72-C as read from Table 1 diagonal). The sum of the linkages from this is 9 +4×3 =21 in agreement with the calculation. The skeletal sketch of the cluster is given in Fig.12.
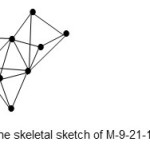 |
Figure 12 Click here to View figure |
The last example11 we can use to illustrate the power of the empirical formula and cluster table is Hg{Fe5(C)(CO)14}22―. For this complex, E = 11×18=198, V = 12+(5×8+4+14×2)x2+2 = 158, k = ½ (E-V)= ½ (198-158) = 20. Hence, its code is M-11-20-158-N. Just by inspection of the k value and the formula, the k value can be split up as follows k =20 = 8+4+8. These can be regarded as linkage fragments which can tentatively give rise to the skeletal structure given in Fig. 13.
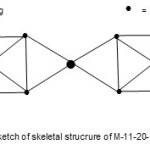 |
Figure 13 Click here to View figure |
The structure indicates two square pyramid units of Fe atoms drawn as seen from above linked to 4 bonds from Hg atom. The carbon atoms are not shown and stereo chemistry not taken into account.
Identifying the Beginning of the Series from the K-Value
There are two approaches in identifying the beginning of a series from a given k value. Consider the complex7, Os9(H)(CO)24―(M-9-20-122-C3C). The complex has a k value of 20. The table shows that the cluster belongs to the clan members of M-9-20-122-C3C series. Also the table shows that the three caps are bestowed onto an octahedral geometry(Oh). Furthermore from the code fragments M-9 and C3, it can readily be deduced that the capping starts at M-6 which is specifically M-6-11-86-C in this case. The table also shows the beginning cluster clan code can easily be traced. This will entail the de-capping descent of ∆k =3. This process is illustrated in scheme 1.
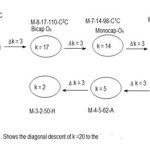 |
Scheme 1 Click here to View Scheme |
This scheme implies that beginning with a hypho cluster of 3 atoms with 2 linkages and 50 valence electrons we can successively generate a butterfly geometry (M-4-5-62-A), followed by a square pyramid geometry (M-5-8-74-N), octahedral geometry (M-6-11-86-C), until we arrive at a tri-capped octahedral geometry of (M-9-20-122-C3C) cluster. The closo series begins with the code M-2-3-30 for two skeletal elements up to M-12-23-170 in the table. The series could be extended as far as possible. Although Table 1 is meant for transition metal carbonyl clusters, it can readily be adapted for use for main group element clusters.
Table 1: Portion of Cluster Series of Transition Metal Carbonyls
| M-2 | M-3 | M-4 | M-5 | M-6 | M-7 | M-8 | M-9 | M-10 | M-11 | M-12 | |
| 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | |
| C7C | M-2-10-16 | M-3-12-30 | M-4-14-44 | M-5-16-58 | M-6-18-72 | M-7-20-86 | M-8-22-100 | M-9-24-114 | M-10-26-128 | M-11-28-142 | M-12-30-156 |
| 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | 25 | 27 | 29 | |
| C6C | M-2-9-18 | M-3-11-32 | M-4-13-46 | M-5-15-60 | M-6-17-74 | M-7-19-88 | M-8-21-102 | M-9-23-116 | M-10-25-130 | M-11-27-144 | M-12-29-158 |
| 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | |
| C5C | M-2-8-20 | M-3-10-34 | M-4-12-48 | M-5-14-62 | M-6-16-76 | M-7-18-90 | M-8-20-104 | M-9-22-118 | M-10-24-132 | M-11-26-146 | M-12-28-160 |
| 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | 25 | 27 | |
| C4C | M-2-7-22 | M-3-9-36 | M-4-11-50 | M-5-13-64 | M-6-15-78 | M-7-17-92 | M-8-19-106 | M-9-21-120 | M-10-23-134 | M-11-25-148 | M-12-27-162 |
| 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | |
| C3C | M-2-6-24 | M-3-8-38 | M-4-10-52 | M-5-12-66 | M-6-14-80 | M-7-16-94 | M-8-18-108 | M-9-20-122 | M-10-22-136 | M-11-24-150 | M-12-26-164 |
| 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | 25 | |
| C2C | M-2-5-26 | M-3-7-40 | M-4-9-54 | M-5-11-68 | M-6-13-82 | M-7-15-96 | M-8-17-110 | M-9-19-124 | M-10-21-138 | M-11-23-152 | M-12-25-166 |
| 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | |
| C1C | M-2-4-28 | M-3-6-42 | M-4-8-56 | M-5-10-70 | M-6-12-84 | M-7-14-98 | M-8-16-112 | M-9-18-126 | M-10-20-140 | M-11-22-154 | M-12-24-168 |
| 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | |
| C | M-2-3-30 | M-3-5-44 | M-4-7-58 | M-5-9-72 | M-6-11-86 | M-7-13-100 | M-8-15-114 | M-9-17-128 | M-10-19-142 | M-11-21-156 | M-12-23-170 |
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | |
| N | M-2-2-32 | M-3-4-46 | M-4-6-60 | M-5-8-74 | M-6-10-88 | M-7-12-102 | M-8-14-116 | M-9-16-130 | M-10-18-144 | M-11-20-158 | M-12-22-172 |
| 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | |
| A | M-2-1-34 | M-3-3-48 | M-4-5-62 | M-5-7-76 | M-6-9-90 | M-7-11-104 | M-8-13-118 | M-9-15-132 | M-10-17-146 | M-11-19-160 | M-12-21-174 |
| 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | |
| H | M-3-2-50 | M-4-4-64 | M-5-6-78 | M-6-8-92 | M-7-10-106 | M-8-12-120 | M-9-14-134 | M-10-16-148 | M-11-18-162 | M-12-20-176 | |
| -1 | 1 | 3 | 5 | 7 | 9 | 11 | 13 | 14 | 16 | 18 | |
| H-1 | M-3-1-52 | M-4-3-66 | M-5-5-80 | M-6-7-94 | M-7-9-108 | M-8-11-122 | M-9-13-136 | M-10-14-150 | M-11-16-164 | M-12-18-178 | |
| -2 | 0 | 2 | 3 | 6 | 8 | 10 | 12 | 13 | 15 | 17 | |
| H-2 | M-4-2-68 | M-5-3-82 | M-6-6-96 | M-7-8-110 | M-8-10-124 | M-9-12-138 | M-10-13-152 | M-11-15-166 | M-12-17-180 |
Table 1 Continued
| M-11 | M-12 | M-13 | M-14 | M-15 | M-16 | M-17 | M-18 | M-19 | M-20 | |
| 30 | 32 | 34 | 36 | 38 | 40 | 42 | 44 | 46 | 48 | |
| C9C | M-11-30-138 | M-12-32-152 | M-13-34-166 | M-14-36-180 | M-15-38-194 | M-16-40-208 | M-17-42-222 | M-18-44-236 | M-19-46-250 | M-20-48-264 |
| 29 | 31 | 33 | 35 | 37 | 39 | 41 | 43 | 45 | 47 | |
| C8C | M-11-29-140 | M-12-31-154 | M-13-33-168 | M-14-35-182 | M-15-37-196 | M-16-39-210 | M-17-41-224 | M-18-43-238 | M-19-45-252 | M-20-47-266 |
| 28 | 30 | 32 | 34 | 36 | 38 | 40 | 42 | 44 | 46 | |
| C7C | M-11-28-142 | M-12-30-156 | M-13-32-170 | M-14-34-184 | M-15-36-198 | M-16-38-212 | M-17-40-226 | M-18-42-240 | M-19-44-254 | M-20-46-268 |
| 27 | 29 | 31 | 33 | 35 | 37 | 39 | 41 | 43 | 45 | |
| C6C | M-11-27-144 | M-12-29-158 | M-13-31-172 | M-14-33-186 | M-15-35-200 | M-16-37-214 | M-17-39-228 | M-18-41-242 | M-19-43-256 | M-20-45-270 |
| 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 | 42 | 44 | |
| C5C | M-11-26-146 | M-12-28-160 | M-13-30-174 | M-14-32-188 | M-15-34-202 | M-16-36-216 | M-17-38-230 | M-18-40-244 | M-19-42-258 | M-20-44-272 |
| 25 | 27 | 29 | 31 | 33 | 35 | 37 | 39 | 41 | 43 | |
| C4C | M-11-25-148 | M-12-27-162 | M-13-29-176 | M-14-31-190 | M-15-33-204 | M-16-35-218 | M-17-37-232 | M-18-39-246 | M-19-41-260 | M-20-43-274 |
| 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 | 42 | |
| C3C | M-11-24-150 | M-12-26-164 | M-13-28-178 | M-14-30-192 | M-15-32-206 | M-16-34-220 | M-17-36-234 | M-18-38-248 | M-19-40-262 | M-20-42-276 |
| 23 | 25 | 27 | 29 | 31 | 33 | 35 | 37 | 39 | 41 | |
| C2C | M-11-23-152 | M-12-25-166 | M-13-27-180 | M-14-29-194 | M-15-31-208 | M-16-33-222 | M-17-35-236 | M-18-37-250 | M-19-39-264 | M-20-41-278 |
| 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 | |
| C1C | M-11-22-154 | M-12-24-168 | M-13-26-182 | M-14-28-196 | M-15-30-210 | M-16-32-224 | M-17-34-238 | M-18-36-252 | M-19-38-266 | M-20-40-280 |
| 21 | 23 | 25 | 27 | 29 | 31 | 33 | 35 | 37 | 39 | |
| C | M-11-21-156 | M-12-23-170 | M-13-25-184 | M-14-27-198 | M-15-29-212 | M-16-31-226 | M-17-33-240 | M-18-35-254 | M-19-37-268 | M-20-39-282 |
| 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | |
| N | M-11-20-158 | M-12-22-172 | M-13-24-186 | M-14-26-200 | M-15-28-214 | M-16-30-228 | M-17-32-242 | M-18-34-256 | M-19-36-270 | M-20-38-284 |
| 19 | 21 | 23 | 25 | 27 | 29 | 31 | 33 | 35 | 37 | |
| A | M-11-19-160 | M-12-21-174 | M-13-23-188 | M-14-25-202 | M-15-27-216 | M-16-29-230 | M-17-31-244 | M-18-33-258 | M-19-35-272 | M-20-37-286 |
| 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | |
| H | M-11-18-162 | M-12-20-176 | M-13-22-190 | M-14-24-204 | M-15-26-218 | M-16-28-232 | M-17-30-246 | M-18-32-260 | M-19-34-274 | M-20-36-288 |
| 17 | 19 | 21 | 23 | 25 | 27 | 29 | 31 | 33 | 35 | |
| H-1 | M-11-17-164 | M-12-19-178 | M-13-21-192 | M-14-23-206 | M-15-25-220 | M-16-27-234 | M-17-29-248 | M-18-31-262 | M-19-33-276 | M-20-35-290 |
| 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | |
| H-2 | M-11-16-166 | M-12-18-180 | M-13-20-194 | M-14-22-208 | M-15-24-222 | M-16-26-238 | M-17-28-250 | M-18-30-264 | M-19-32-278 | M-20-34-292 |
Table 2: Categorization of Selected Carbonyl Cluster Complexes
| Complex | E | V | k | Cluster Series *Category | Comment |
| Re2(H)2(CO)8 | 36 | 32 | 2 | M-2-2-32-N | Linear (double bond) |
| Re2(CO)10 | 36 | 34 | 1 | M-2-1-34-A | Linear (single bond) |
| Re3(H)3(CO)102- | 54 | 46 | 4 | M-3-4-46-N | Triangle |
| Re3(H)2(CO)12― | 54 | 48 | 3 | M-3-3-48-A | Triangle |
| Re4(H)4(CO)152- | 72 | 64 | 4 | M-4-4-64-H | Square |
| Re4(H)4(CO)132- | 72 | 60 | 6 | M-4-6-60-N | Tetrahedral (Td) |
| Re4(H)6(CO)122― | 72 | 60 | 6 | M-4-6-60-N | Tetrahedral (Td) |
| Re4(H)5(CO)12– | 72 | 58 | 7 | M-4-7-58-C | |
| Re4(CO)162- | 72 | 62 | 5 | M-4-5-62-A | Butterfly |
| Re4(H)5(CO)14― | 72 | 62 | 5 | M-4-5-62-A | Butterfly |
| Re4(H)4(CO)12 | 72 | 56 | 8 | M-4-8-56-C1C | |
| Re5(C)(CO)16(H)2- | 90 | 74 | 8 | M-5-8-74-N | Square pyramid (C4v) |
| Re6(H)8(CO)182- | 108 | 88 | 10 | M-6-10-88-N | |
| Re6(C)(CO)192- | 108 | 86 | 11 | M-6-11-86-C | Octahedral (Oh) |
| Re6(C)(CO)19(H)― | 108 | 86 | 11 | M-6-11-86-C | Octahedral (Oh) |
| Re6(C)(CO)18(H)22― | 108 | 86 | 11 | M-6-11-86-C | Octahedral (Oh) |
| Re6(C)(CO)18(H)3― | 108 | 86 | 11 | M-6-11-86-C | Octahedral (Oh) |
| Re7(C)(CO)213― | 126 | 98 | 14 | M-7-14-98-C1C | Monocap based on Oh(11+3 = 14) |
| Re7(C)(CO)21(H)2― | 126 | 98 | 14 | M-7-14-98-C1C | Monocap based on Oh(11+3 = 14) |
| Re7(C)(CO)21(H)2― | 126 | 98 | 14 | M-7-14-98-C1C | Monocap based on Oh(11+3 = 14) |
| Re7(C)(CO)22― | 126 | 98 | 14 | M-7-14-98-C1C | Monocap based on Oh(11+3 = 14) |
| Re8(C)(CO)22― | 144 | 110 | 17 | M-8-17-110-C2C | Bicap based on Oh(11+3+3 = 17) |
| Os5(CO)16 | 90 | 72 | 9 | M-5-9-72-C | Trigonalbipyramid (TBP,D3h) |
| Os5(CO)15(H)― | 90 | 72 | 9 | M-5-9-72-C | Trigonalbipyramid (TBP,D3h) |
| Os6(CO)18 | 108 | 84 | 12 | M-6-12-84-C1C | Monocap based on TBP(9+3 = 12) |
| Os6(CO)182― | 108 | 86 | 11 | M-6-11-86-C | Octahedral (Oh) |
| (H)Os6(CO)18― | 108 | 86 | 11 | M-6-11-86-C | Octahedral (Oh) |
| (H)2Os6(CO)18 | 108 | 86 | 11 | M-6-11-86-C | Square pyramid –monocap(8+3 = 11) |
| Os6(CO)17L4 | 108 | 90 | 9 | M-6-9-90-A | A triangle on top of |
| L = P(OMe)3 | 2 atom linked triangles | ||||
| H)2Os6(CO)19 | 108 | 88 | 10 | M-6-10-88-N | |
| Os7(CO)21 | 126 | 98 | 14 | M-7-14-98-C1C | Monocap based on Oh(11+3 = 14) |
| Os7(CO)21(H)2 | 126 | 100 | 13 | M-7-13-C |
*C = CLOSO, N = NIDO, A = ARACHNO, H = HYPHO, C1C = MONOCAP, C2C = BICAP, etc, H-1 = FIRST SERIES BELOW HYPHO, H-2 = SECOND SERIES BELOW HYPHO, etc.
| Os7(CO)22(H)2 | 126 | 102 | 12 | M-7-12-N | |
| (H)2Os7(CO)20 | 126 | 98 | 14 | M-7-14-98-C1C | Bicap Td with a leg linkage(6+3+3+2 =14) |
| Os8(CO)222― | 144 | 110 | 17 | M-8-17-110-C2C | Bicap based on Oh(11+3+3 =17) |
| (H)Os8(CO)222― | 144 | 110 | 17 | M-8-17-110-C2C | 2 Edge-fused Td units each monocapped. |
| Os9(CO)242― | 162 | 122 | 20 | M-9-20-122-C3C | Tricapped based on Oh(11+3+3+3) =20) |
| Os9(H)(CO)24― | 162 | 122 | 20 | M-9-20-122-C3C | Tricapped based on Oh(11+3+3+3) =20) |
| Os10(C)(CO)242― | 180 | 134 | 23 | M-10-23-134-C4C | Tetracapped based on Oh(11+3+3+3+3 = 23) |
| Os10(CO)262― | 180 | 134 | 23 | M-10-23-134-C4C | Tetracapped based on Oh(11+3+3+3+3 = 23) |
Special Cluster Series
There are special cluster series that are usually encountered in chemistry. Some of these are given in Table 3.
Table 3: Important cluster series normally encountered
| Mx | k | V | Category Code | Corresponding Code Main Group Element | Possible skeletal geometry |
| 2 | 1 | 34 | M-2-1-34-A | M-2-1-14-A | Linear, single bond |
| 2 | 2 | 32 | M-2-2-32-N | M-2-2-12-N | Linear, double bond |
| 2 | 3 | 30 | M-2-3-30-C | M-2-3-10-C | Linear, Triple bond |
| 2 | 4 | 28 | M-2-4-28-C1C | M-2-4-08-C1C | Linear, Quadruple bond |
| 3 | 3 | 48 | M-3-3-48-A | M-3-3-18-A | Triangle |
| 4 | 6 | 60 | M-4-4-60-N | M-4-4-20-N | Td |
| 5 | 9 | 72 | M-5-9-72-C | M-5-9-22-C | Trigonalbipyramid |
| 5 | 8 | 74 | M-5-8-74-N | M-5-8-24-N | Square pyramid |
| 6 | 11 | 86 | M-6-11-86-C | M-6-11-26-C | Oh |
| 6 | 10 | 90 | M-6-9-90-A | M-6-9-30-A | Trigonal Prism |
| 7 | 14 | 98 | M-7-14-98-C1C | M-7-14-28-C1C | Monocap-Oh |
| 8 | 17 | 110 | M-8-17-110-C2C | M-8-17-300-C2C | Bicap-Oh |
| 9 | 20 | 122 | M-9-20-122-C3C | M-9-20-32-C3C | Tricap-Oh |
| 10 | 23 | 134 | M-10-23-134-C4C | M-10-23-34-C4C | Tetracap-Oh |
Magic Cluster Ratio (1:2:14)
Consider the cluster category code of the mono-cap series (C1C). The selected ones are given in Table 4.
Table 4: Magic Cluster Ratio
| Code: M-x-k-V | Magic cluster ratio:-M-x:k:V |
| M-2-4-28 | 1:2:14 |
| M-3-6-42 | 1:2:14 |
| M-4-8-56 | 1:2:14 |
| M-5-10-70 | 1:2:14 |
| M-6-12-84 | 1:2:14 |
| M-7-14-98 | 1:2:14 |
| M-8-16-112 | 1:2:14 |
| M-9-18-126 | 1:2:14 |
| M-10-20-140 | 1:2:14 |
| M-11-22-154 | 1:2:14 |
| M-12-24-168 | 1:2:14 |
| M-13-26-182 | 1:2:14 |
| M-14-28-196 | 1:2:14 |
| M-15-30-210 | 1:2:14 |
| M-16-32-224 | 1:2:14 |
| M-17-34-238 | 1:2:14 |
| M-18-36-252 | 1:2:14 |
| M-19-38-266 | 1:2:14 |
| M-20-40-280 | 1:2:14 |
From this table, a constant ratio of 1:2:14 is discerned. The reason for this phenomenon is not clear yet.
Conclusion
Simple and relatively more complex transition metal carbonyl clusters can be analyzed using basic number theory. The cluster number k value is obtained from the empirical formula k = ½ (E-V). The cluster numbers have been utilized to construct a user friendly cluster table for classifying clusters into category series. The cluster number, k value can be used to categorize a given carbonyl cluster. The k value may simply be regarded as the number of bonds or linkages or ‘pillars’ that hold a given cluster system together. Furthermore, from the k value with or without the help of the cluster table the skeletal geometry of the cluster may tentatively derived. By this approach, the skeletal structures of metal carbonyls from simple to relatively more complex can greatly be appreciated without prior knowledge of the polyhedral skeletal electron pair theory12, Jemmis rules13 or topology concepts14. Nevertheless, this work complements the existing knowledge on carbonyl clusters. The author believes method will be enjoyed by a wide spectrum of scholars mainly undergraduate, postgraduate chemistry students as well as chemistry teachers in secondary schoolsor high schools due to its simplicity.
Dedication
This paper is dedicated to Charles Alfred Coulson(1910-1974) who once briefly taught the author in Africa, Gilbert Newton Lewis(1875-1946) and Irving Langmuir(1881-1957).
Acknowledgement
I wish to acknowledge the University of Namibia for provision of facilities and financial assistance, NAMSOV, Namibia for the timely research grant and my wife for the encouragement to write this article.
References
- Kiremire, E. M. R., Daniel, L. S, Hishimone, P., Orient. J. Chem., 2014, 30(3), 923-932.
- Kiremire, E. M. R., Orient. J. Chem., 2014, 30(3), 1055-1060.
- Kiremire, E. M. R., Orient. J. Chem., 2014, 30(4), in press.
- Kiremire, E. M. R., Orient. J. Chem., 2007, 32(2), 809-812.
- Kiremire, E. M. R., Kiremire, E. B. B., Orient. J. Chem., 2007, 4(1), 09-18.
- Teo, B. K., Longoni, G., Chung, F. R. K., Inorg. Chem., 1984, 23, 1257-1266.
- Hughes, A. K., Wade, K., Coord. Chem. Rev., 2000, 197, 191-229.
- Couture, C., Farrar, D. H., J. Chem. Soc., Chem. Commun.,1985, 197-198.
- Couture, C., Farrar, D. H., J. Chem. Soc.,Dalton, Trans., 1986, 1395-1402.
- Ahkter, Z., Edwards, A., Ingham, S. L., Lewis, J., Castro, A. M. M., Raithby, P. R., Shields, G. P., J. Cluster Sci., 2000, 11, 217-226.
- Reina, R., Riba, O., Rossell, O., Seco, M., Gómez-Sal, P., Martin, A., de Montauzon,D., Mari, A., Organometallics, 1998,17,4127-4135.
- Welch, A. J., J. Chem. Soc., Chem. Commun., 2013, 49, 3615-3616.
- Jemmis, E. D., Balakrishnarajan, M. M., J. Am. Chem. Soc., 2001, 123, 4324-4330.
- King, R. B., Inorg. Chim. Acta, 1986, 116, 99-107.

This work is licensed under a Creative Commons Attribution 4.0 International License.









