Theoretical Investigation of Tautomerism Stability of  Hydantoin in the Gas Phase and in the Solution

Introduction

Intramolecular 1,3-proton transfer of the keto-enol reactions of heterocyclic systems with several basic centers, O, N, S and Se atoms, are of great interest to medicinal and biochemical applications. Also, understanding of the relative stabilities of heterocyclic tautomers and any subsequent conversions between tautomeric forms is very vital for both structural chemists and biologists [1,2]. Along this line, relative stabilities of various tautomeric structures of five-, six- and seven-membered ring (dioxo, oxo/thio, oxo/seleno, dithio and diseleno combinations) were investigated using both theoretical and experimental tools[3-12]. Both tools indicate that in these compounds the thioxo, selenooxo, dioxo, dithio or diseleno tautomer is most stable.

 

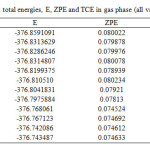TableS1: Single-point total energies, E, ZPE and TCE in gas phase (all values are in hartree): Click here to View table

 

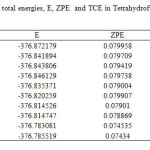TableS2: Single-point total energies, E, ZPE  and TCE in Tetrahydrofuran, THF (All values are in hartree).  Click here to View table

 

Particularly important are hydantoins for having different therapeutic activities including anticonvulsants, antiarrhythmic, bactericides, fungicides, and anticancer. Their anticonvulsant activity has been investigated for tens of years [13-18]. Chemically, hydantoin (glycolurea, 2,4-Imidazolidinedione) and its derivatives, Scheme 1, have two N-H bonds in a molecule. One is adjacent to a carbonyl radical and other, surrounded by two carbonyl radicals. They form  two chains linked by N-H···O hydrogen bonds, from which inversion centers create a chain of rings. The chemical reactivity of hydantoins is primarily determined by the stability of their corresponding tautomers [19,20].

 

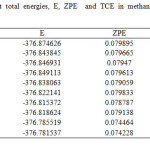TableS3: Single-point total energies, E, ZPE  and TCE in methanol (All values are in hartree).   Click here to View table

 

The common studies of tautomerisation of carbonylic compounds such as uracil, thiouracil, 1, 2, 4-triazepines, oxazolidine and thiazolidine, can anticipate that hydantoin may exhibit five different five different tautomeric structures with different conformations [21]. In addition, three different dihydroxy tautomeric structures with different conformations can also formed by a second isomerization [22]. Previous experimental and theoretical studies [21-27] of hydantoin and some of its derivatives either in neutral, protonated and deprotonated forms showed that the preferred existence of the hydantoins as lactam tautomer (diketo form) ((the lactam tautomer is at least 10.6 kcal/mol^-1 (PM3), 15.6 kcal/mol (AM1) or 17.0 kcal/mol (B3LYP),  respectively, more stable than any other tautomer [21, 25]).

 

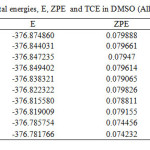TableS4: Single-point total energies, E, ZPE  and TCE in DMSO (All values are in hartree).  Click here to View table

 

Recently, Shabanian M. et al [24] studied the solvation effects on the tautomerism of N₁-substituted hydantoin. They found, in all cases, that the diketo form is the most stable tautomer and the solvent interactions have not pronounced an effect on the order of the stability of the tautomers in the gas. They also found that there is a significant solvent effect on the dipole moment of the individual tautomers, which is increased by change the solvent from gas to the solution as well as by increasing the solvent polarity.

This study employs density functional theory (DFT) on the investigation of those structures and to present a complete analysis of their relative stabilities in the gas phase and deferent solution with different dielectric constant, named, water (THF (e=7.0, methanol (e=33.0), DMSO (e=50.0) and water (e=78.8). This work includes variation of dipole moments and NBO charges on atoms in the solvents and gas phase. Also, this works involves a detail study on the geometrical structures (bond lengths, bond angles and vibrational frequencies). Finally, the charge densities of the carbonyl group, the bonds within the hydantoin moiety before and after tautomerisation, as well as the hydroxyl group formed due to the tautomerisation process, based on the AIM theory of Bader will be discussed [27].

Computational methods

All compound’s structures were drawn using Gauss View 5.01. To characterize all the optimized geometries the standard hybrid density functional theory (DFT) in the framework of B3LYP [28,29] functional at the 6-311+‏G(d,p) basis function was used. The harmonic vibrational frequencies of the different stationary points of the potential energy surface (PES) have been calculated at the same level of theory used to check that all the structures are minma with no imaginary frequencies, as well as to estimate the corresponding zero-point energy corrections (ZPE) that were scaled by the empirical factor 0.9806 proposed by Scott and Radom [30]. In order to obtain more reliable energies for the local minima, final energies were evaluated using B3LYP/6-311++G(3df,2p) level of theory.

The tautomers were also optimized in solvents according to the integral equation formalism polarizable continuum model  (IEF-PCM) of  Tomasi and co-workers, which exploits the generating polyhedra procedure [31-34] to build the cavity in the polarisable continuum medium, where the solute is accommodated. We have additionally carried out a single point calculation to compute the atomic charges in all the structures using the Natural Population Analysis (NPA) method with the Natural Bond Orbital (NBO) approach  [35] to obtain the natural atomic orbital energies and the natural population of the atomic charges. Finally Analysis of the electron densities at bond critical points (bcps) of the optimized structures was calculated by generating the wave functions through a single point calculation on the geometrized structures and analyzed these wave functions by means of the atoms in molecules (AIM) theory proposed by Bader et al. [27] as implemented in AIM2000 program package [36]. All calculations were carried out with the GAUSSIAN 09 package [37].

 

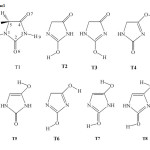Scheme 1  Click here to View Scheme

 

Results and discussion

Gas Phase Relative stabilities

Structures and numbering of hydantoin (2,4-dioxoimidazoildine) are depicted in Scheme 1. The results of energy comparisons of eight tautomers in the gas phase and different solvents are summarized in Table 1. Full set of data are given in Table S1-S5 of supplementary material. A cursory examination of this table shows that the DFT B3LYP calculations find the diketo tautomer to be at least 17.0 kcal/mol more stable than the others (Scheme 1). This result has been taken as an unequivocal proof for the studied hydantoins to exist preferentially as the lactam tautomer. These findings agree with published theoretical and experimental studies for hydantoin and its derivatives [20-25], which also concluded that the dione tautomer, T1 is the most stable one.

Our results show that the most stable oxo-hydroxy form corresponds to isomer T2, which is formed due to the migration of the amino hydrogen atom (H8) to the adjacent carbonyl oxygen atom (O6). Contrary to Kleinpeter et al, [22] isomers T2 and T4, which is formed due to the of hydrogen atom (H9) to the adjacent oxygen atom (O7) are almost degenerate while the relative stabilities of tautomers. The advantage of the C2=O6 over the C4=O7 may be attributed to the presence of the former group between two -NH groups, which donate electron to C2=O6 group and make it more basic than the latter one and available to interact with the migrated hydrogen atom.

On the other hand, the most stable dienol structure corresponds to isomer T6, which lays ~ 31 kcal/mol less stable than the global minimum (isomer T1). It is worth to mention that isomer T6 is formed due to the migration of the hydrogen atoms (H8 and H9) to the oxygen atoms (O6 and O7), whereas the other dihydroxy structures can be yielded by the migration of the methyl hydrogen atom (H10) and H8 or H9 to the adjacent carbonyl groups, (C2=O6) and C4=O7). Therefore, the order of stability of all the tautomers in gas phase is T1 > T2 > T4 > T3 > T5 > T6 > T7 > T8.

 

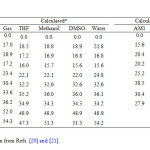Table1: Relative energies (in kcal/mol) of the different tautomers of hydantoin. Click here to View table

 

Gas Phase Prototropic Intramolecular Tautomerisation 

A possible prototropic isomerisation in gas phase is being explored by analyzing the energy profiles of the transition states connecting the diketo form of T1, the most stable isomer from one side, and at the other side one of the two most stable oxo-hydroxy structures of each of our systems. Energy profiles computed at B3LYP/6-311+G(3df,2p)//B3LYP/6-311+(d,p) level of theory are shown in Figure 1. Activation energy barriers of all possible transition states involved in the mechanisms are also depicted in the same figure, as well as the relative energy values corresponding to the most stable isomers as listed in Table 1.

For mono-enolization process, as indicated above, tautomer T1 is the most stable one, but there are significant differences regarding the relative stabilities of the remaining isomers. The first important differences affect the enolization mechanism of the oxo group attached to C2 and C4. The enolization can be produced either by one of the following three ways:-

• a 1,3-H shift from the N1–H to yield species T2 via TS12,
• a 1,3-H shift from the N1–H to yield species T3 and T4 via TS13 and TS14, respectively, or
• by a 1,3-H shift from the CH₂ group to yield isomer only through TS15.

As mentioned above, the tautomers B and D are almost degenerate. However, the transition state TS12 is 0.9 kcal/mole lower than that connecting between T1 and T4, TS14. In other word, the 1,3 hydrogen shift from tautomer T1 to tautomer T2 through the TS12 is slightly favored over that from species T1 to species T4 to through TS14. This finding clearly indicates that there is a  competiveness between the two carbonyl groups, (C2=O6) and C4=O7), to undergo the intramolecular prototropic tautomerisation. Our results lead us to conclude that this reaction at O6 is energetically favored over the corresponding O7.

 

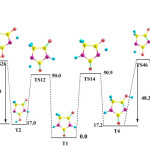Fig1: Energy profiles corresponding to the possible mechanisms connecting T1 and T2, T4 and T6 isomers. Values are in kcal/mol.  Click here to View Figure

 

For the dihydroxy tautomers, T6, T7 and T8, these species are formed by two steps. First step consists of enolization of one of the two carbonyl groups by a 1,3-H transfer to form as previously discussed. The step corresponds to another 1,3-H migration to the other carbonyl group via a new transition. In our case, we will discuss only two mechanisms, formation of T6 from T2 and T4 through transition states TS24 and T46 respectively, are presented in Fig. 1. Our results indicate that the overall activation energies required to yield T6 through the two mechanisms are extremely high (³ 65.5). Obviously, because of the high energy barrier, the intramolecular prototropic tautomerisation in both cases is thermodynamically unfavored and the tautomer T1 is predominant in gas phase.

Gas Phase Geometrical and Topological Properties

For the sake of conciseness we will discuss only the structure of isomers T1, T4 and T6. The most relevant geometrical structures and topological parameters are summarized in Table 2 and their gas phase optimized structures and corresponding molecular graphs, obtained by using the AIM theory of Bader through the using of the AIM2000 suite of program, are shown in Figure 1. Full set of data are available upon request. It is found that the optimized geometry of the title compound calculated by the B3LYP method of DFT in different solvents agrees well with the experimental and the theoretical results (Table 2).

 

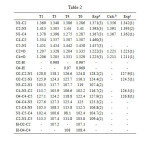Table2:  Structural parameters of the optimized geometries of some tautomers of hydantoins in gas phase. Bond lengths in angstroms and Bond angles in degree.  Click here to View table

 

It is noting that the intrinsic characteristics of the carbonyl group change slightly depending on their relative position within the ring. When they are attached at C2, the corresponding C=O bond is slightly stronger as reflected in a larger charge density at the bond critical point (see Table 3 and Figure 2) and in a slightly greater bond length. Indeed, for tautomer T1, while for C2=O the charge density is 0.422 a.u. and the bond length is predicted to be 1.207 Å, for the C4=O the charge density is calculated to be 0.420 a.u. and the bond length is calculated to be 1.206 Å. (see Table 2 and 3).

 

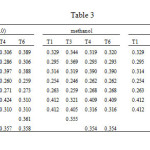Table3: Charge densities (r) at the bond critical point of different tautomers of hydantoin in gas phase and in solution. The values are in a.u.  Click here to View table

 

Comparing of the geometrical structures and topological properties of both T2 and T4 on the one hand and of the species T3 and T5 on the other hand, leads us to remark the following notes:-

• For isomer T1 and T4, the C2-O and C4-O are almost equal in strength as reflected in their charge density values at the bond critical point (0.310 a.u.) and they have nearly the same bond length. Indeed, our results show that C2-O is 0.006 Å longer than the C4-O. These results reflect that the two carbonyl oxygen atom have almost the same intrinsic characteristics.
• For isomer T3 and T5, the bond lengths of C2-O and C4-O are calculated to be 1.328 and 1.329 Å, respectively, which are 0.009 Å shorter than the corresponding ones in species T2 and T4. Their charge densities are  predicted to be 0.3158 and , which is ~0.006 a.u. greater than the same bond in species T2 and T4 (Table 2 and 3) . These results indicate that the carbonyl oxygen atoms in the T2 and T4 have stronger intrinsic characteristics than the analogue ones in species T3 and T5, explained why the former species are more stable than the latter ones.

 

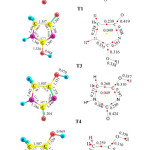Fig2: (Left) Gas phase optimized geometries of the most stable diketo, enol and dienol tautomers  (T1, T4 and T6). Bond lengths are in angstroms. (Right): Molecular graphs for the same tautomers Red dots and yellow dots are bond critical point and ring critical points, respectively. Charge densities are in a.u.   Click here to View Figure

 

Analysis of dipole moments and NBO charges

Calculated dipole moments of optimized tautomers of hydantoin in gas phase and in solution at B3LYP/6-311+G(d,p) level of theory are collected in Table 4. Our results show that species T2 with 2.57D has dipole moment smaller than that of the global minimum T1 with 2.73D. Also, T7 tautomer, with two hydroxyl groups and N1=C2 and C4=C5 bonds, has the smallest dipole moments than the other seven forms with 1.58D. T8 tautomer with C2=N3 and C4=C5 has the largest dipole moments with 6.22D and 8.25D in gas phase and in water.

 

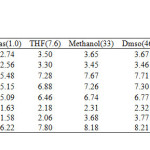Table4: Calculated dipole moments of optimized tautomers of hydantoin (Deby)  Click here to View table

 

Calculated NBO charges using the natural population analysis (NPA) of optimized structures of hydantoin tautomers in the gas phase and in solvents at B3LYP/6-311+G(d,p) level of theory are listed in Table 5. on ring atoms of hydantoin as well as on the carbonyl oxygen atoms in gas phase and in solution have been listed in Table 5. For T1 tautomer, the negative charge on O6 is calculated to be 0.033 a.u larger than that on O7, which suggests that O6 is more basic than the O7. This finding indicates that the  preferred site for the prototropic intramolecular tautomerisation is preferred the carbonyl atom attached to position 2 of the hydantoin ring. On the other hand, the two nitrogen atom at position 1 and 3 carries almost the same negative value (~ 0.661 au.) with difference of ~ 0.0007 au. in favor of N1, suggesting that the H8 and H9 have almost the same acidity character.  For T2 form, the negative charge on O6 atom is found to be larger than that on O6 in T3, and O7 in both T4 and T5 species. Indeed, in T2 and T3, the NBO charge on O6 is calculated to be -0.667 a.u. in the former and -0.653 a.u. on the latter, while, the negative charges on O7 in T4 and T5 species are found to be -0.653 and -0.647, respectively. These results enhance the tautomers stability order discussed above. Additionally, in all species, our results indicate that carbon atom at position 2 carries the largest positive charge and these positions will most effectively interact with nucleophiles. Whereas carbon atom at position 5 carries negative charge and this position will most effectively with electrophiles.

 

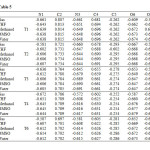Table5: Calculated NBO charges on the ring atoms and the carbonyl oxygen atoms of hydantoin (a.u.)  Click here to View table

 

Solvent effects

It is well known that solvent effects are relevant in tautomers stability phenomena, since polarity differences among tautomers can induce significant changes in their relative energies in solution. IE-PCM/B3LYP calculations were used to analyze the solvent effects on tautomerism of hydantoin. It is important to stress that the PCM model does not consider the presence of explicit solvent molecules; hence specific solute–solvent interactions are not described and the calculated solutions effects arise only from mutual solute–solvent electrostatic polarization. So that some points should be remarked as follow

• The data presented in Table 1 show that as, regardless of the solvent nature, the diketo form (tautomer T1) is the most stable tautomers among all the tautomers under investigation.
• For all solvents, tautomer T4 is the most stable oxo-enol structure and T7 is the least stable dihydroxy one. The stability trend becomes T1 > T4 > T3 > T2 > T5 > T6 > T8 > T7.
• The relative energy difference between the diketo form (tautomer T1) and the first stable oxo-hydroxy structure decreases when changing from gas phase to the more polar solvent. Indeed, for tautomer T4, when changing from gas phase to water the relative energy decreases from 17.2 – 15.6 kcal/mol.
• Interestingly, the energy gap of the isomerization process, which connects between the different isomers and the global minimum (T1) is found to be decreased when changing from gas phase to more polar solvents (water) (see Table 1 and Figure 3).

 

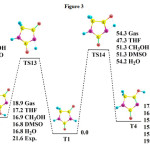Fig3: Energy profiles corresponding to the possible mechanisms connecting T1 and T3, T4 in different solvents. Values are in kcal/mol.  Click here to View Figure

 

• The dipole moments increases by changing the gas phase to the solvent as well as by increasing the solvent polarity. The most significant variations being obtained in tautomer T3, which increases by 2.27 D when changing from the gas phase to the most polar solvent (water). Whereas the least significant variations being obtained for T6 with 0.7 D when going from gas phase to water (see Table 4).
• We have examined the charge distribution of tautomers in the solvent as well as gas phase by using calculated NBO charges. The charge distribution in solvents with increase of polarity differently varies for any atoms.
• We have also examined the charge densities (r) at bond critical points in solvent as well in gas phase by using AIM theory of Bader. It is found that when changing from non-polar to polar solvent the charge density varies by decreasing or increasing for any bond.

Conclusion

The relative stability of the oxo and thio derivatives of hydantoin are rather similar to those reported in the literature for uracil and its thio derivatives, oxazolidine, thiazolidine and 1,2,4-triazepines. The most stable tautomer corresponds to the diketo structure, followed by the corresponding oxo-hydroxy forms, while the dihydroxy structures are the least stable ones. Total energies of all forms are affected by solvent. With increase of polarity total energy of all compounds were more negative. As for uracil, thiazolidine, oxazolidine and triazepines derivatives, the tautomerism activation barriers are high enough as to conclude that only the dioxo structures should be found in the gas phase. The relative stabilities should change, however, in more polar solvent because the corresponding prototropic tautomerism reactions  are accompanied by significant changes in the dipole moment of the system.

The dipole moments of all compounds are affected by solvent. With increase of the polarity of solvents the dipole moments of all tautomers were increased. The NBO charges on all seven atoms were affected by solvents. In addition with increase of dielectric constant a variation was found.

The bonding characteristics of the carbonyl groups depend on their relative positions. When these groups are attached to C2, the C=O linkage is stronger than when it is attached to position 4. This is clearly reflected in the reactivity of these systems in the gas phase.

Acknowledgments

A generous allocation of computational time at the Scientific Computational Center (CCC) of the Universidad Autónoma de Madrid (Spain) acknowledged.

References

1. Elguero J.; Katritzky A. R.; Denisko O., Adv Heterocycl Chem., 2000, 76, 1-84.
2. Minkin V. I.; Garnovski A. D.; Elguero J., Katritzky A. R.; Denisko O., Adv. Heterocycl. Chem., 2002, 38, 1110-1120.
3. Tahmassebi D., J. Mol. Struct. (THEOCHEM)., 2003, 638, 11-20.
4. Agelova S.; Enchev V.; Markova N.; Denkova P.; Kostova K., J Mol Struct., (THEOCHEM), 2004, 711, 201-207.
5. Santos M.; Junior M.; Oliviera S.; da Silva J.; Lima M.; Lima M.; Galdino S.; Pitta I., J. Mol. Struct., (THEOCHEM), 2005, 715, 191-201.
6. Lamsabhi M.; Alcami M.; Mo O.; Bouab W.; Esseffar M.; Abboud J. L. M.; Yanez M. J. Phys. Chem., A, 2000, 104, 5122-5130.
7. Lamsabhi M.; Esseffar M.; Bouab W.; El Messaoudi T.; Abboud J. L. M.; Alcami M.; Yanez M., J. Phys. Chem., A., 2002, 106, 7383-7389.
8. Allegretti P.; Labadier G.; Sierra M.; Furing J., Afinidad LVII, Enero-Febrero 2000, 485, 41-49.
9. Lamsabhi M.; El Messaoudi T.; Esseffar M.; Alcami M.; Yanez M., New J. Chem., 2002, 26, 711-719.
10. Yu F.-L.; Schwalbe C. H.; Watkin D., Acta Cryst., 2004, C60, 714-717.
11. Sabih K.; and Sabih K., Anal. Chem., 1969, 41, 1452-1454.
12. Shabanian M.; Moghanian H.; Hajibeygi M.; Mohamadi A., E-J. Chem., 2012, 9, 107-112.
13. Locock R. A.; Coutts R. T., Org. Mass Spectrom, 1970, 3(6), 735-745.
14. Camerman K.; Camerman N., Acta Cryst., 1971, B27, 2205-2211.
15. Simig Gy.; Lemport K.; Tamas J.; Czria G., Tetrahedron, 1975, 31, 1195-1306.
16. Schmidt M. W.; Baldridge K. K.; Boatz J. A.; Jenesen J. H.; Koseki S.; Gordon M. S.; Yadav A.; Yadav V. K., J. Mol. Struct., (THEOCHEM), 1994, 315, 245-256.
17. Keinpeter E., Struct. Chem., 1997, 8, 161-173.
18. Nguyen K. A.; Windus T. L.; Albert S. T., QCPE Bull., 1990, 10, 52-54.
19. Bovamick N.; Clarke H. T., J. Am. Chem Soc., 1938, 60, 2426.
20. Piasek Z.; Urbanski T.; Tetrahedron Lett.,, 1962, 16, 723-727.
21. Hawkes G.E.; Randall E.W.; Hull W.E.; J. Chem. Soc., Perkin, 1977, 2,  1268-1275.
22. Kleinpeter E.; Heydenreich M.; Kalder L.; Koch A.; Henning D.; Kempter G.; Benassi R.; Taddei F., J. Mol. Struct. 1997, 403, 111-122.
23. Allegretti P. E.; Labadie G. R.; Sierra M. G.; and Furing J.P., Afinidad-BARCELONA, 2000, 57, 41-49.
24. Shabanian M.; Moghanian H.; Hajibeygi M.; Mohamadi A.; Arabian J. Chem. 2011, in press.
25. Safi Z. S.; Abu-Awwad F. M., E-J. Chem., 2008, 5, 884-915.
26. Safi Z.; G. Frenking G., Int. J. Quant. Chem, 2013, 52, 908-.
27. Safi Z., European Journal of Chemistry, 2012, 3(3), 348-355
28. R.F.W. Bader; “Atoms in Molecules – A Quantum Theory”, Oxford University Press, Oxford, UK, 1990.
29. Becke A.D., J. Chem. Phys, 1993, 98, 5648-5652.
30. Lee C.; Yang W.; Parr R.G., Phys. Rev. B, 1988, 37, 785-789.
31. cott A. P.; Radom L., J. Phys. Chem. 1996, 100, 16502-16513.
32. Miertus S.; Scrocco E.; Tomasi J., J. Chem. Phys., 1981, 55, 117-129.
33. Cances M. T.; Mennucci V.; Tomasi J., J. Chem. Phys., 1997, 107, 3032-3041.
34. Cossi M.; Barone V.; Mennucci B.; Tomasi J., Chem. Phys. Lett., 1998, 286, 253-260.
35. Barone V.; Cossi M.; Tomasi J., J. Comp. Chem., 1998, 19, 404-414.
36. Reed A. E.; Weinstock R. B.; Weinhold F., J. Phys. Chem., 1985, 83 735-746.
37. F. Biegler-König. AIM2000, University of Applied Sciences, Bielefeld, Germany, (2000).
38. M. J. Frisch, et al Gaussian 09; Gaussian, Inc., Pittsburgh, PA, 2009.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.