ISSN : 0970 - 020X, ONLINE ISSN : 2231-5039
     FacebookTwitterLinkedinMendeley

Numerical Sequence of Borane Series

Volume 30, Number 3

Enos Masheija Kiremire

Department of Chemistry and Biochemistry, University of Namibia, Private Bag 13301, Windhoek, Namibia

DOI : http://dx.doi.org/10.13005/ojc/300317

Article Publishing History
Article Received on :
Article Accepted on :
Article Published : 18 Sep 2014
Article Metrics
ABSTRACT:

A table of hydroborane families has been created. The table links boranes of different families(homologous series) and members of the same family based on k number. The table is useful deducing straight away whether a borane( molecular formula) is closo, nido or arachno or something else. The table also indicates that boranes are formed according to natural periodic function (arithmetical progression). The empirical formula utilized is extremely versatile, simple and based on the principle of Nobel gas configuration. It could be used in both simple and complex boranes and carboranes. The closo members which portray characteristic shapes also have characteristic k1 numbers.

KEYWORDS:

Numerical Sequence; hydroborane; number

Download this article as: 

Copy the following to cite this article:

Kiremire E. M. Numerical Sequence of Borane Series. Orient J Chem 2014;30(3).

Copy the following to cite this URL:

Kiremire E. M. Numerical Sequence of Borane Series. Orient J Chem 2014;30(3). Available from: http://www.orientjchem.org/?p=4768

INTRODUCTION

As a result of the carbon (C) atom to catenate and also form strong bonds with a hydrogen atom, it is able to generate a vast range of families of hydrocarbons. Some of the common families may be given by the formulas

F1 = CnH2n+2 (alkanes), F2 = CnH2n (alkenes), and F3 = CnH2n-2 (alkynes).

For each of these families, the carbon atom obeys the octet (8) rule which has its base in a noble gas configuration of neon (Ne). On the other hand the boron atom (B) which is next to the carbon atom one valence electron less, mimics the carbon atom to produce boron hydrides (boranes) in an attempt to obey the octet rule. For instance, diborane B2H6 = (BH)2H4 may regarded as attempting to mimic C2H4 since (BH) fragment is electronically equivalent to (C) atom. Indeed, their shapes could be viewed as indicated in the sketch of Fig. 1.  The two hydrogen atoms indicated by dots in the two bonds, can be considered to donate two electrons into the diboranemolecule so as to enable the boron atoms to satisfy the octet rule. In reality, it should be noted that diborane has two banana bonds of bridging H atoms.

 

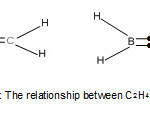Figure 1 Figure 1 A

Click here to View Figure

 

BORANE SERIES

Just like hydrocarbons, the known boron hydrides have been grouped into families. These  families are known as CLOSO, NIDO, ARACHNO and HYPO and the rare one KLADO.  These families may be represented by the formulas given below.

G0 = BnHn , G1 = BnHn+2 (CLOSO), G2 =  BnHn+4(NIDO) , G3 = BnHn+6 (ARACHNO) , G4 = BnHn+8 (HYPO), G5 = BnHn+10 (P =KLADO), G6 = BnHn+12 (Q),G7 = BnHn+14(R). These series (families) are given in Table 1. Each member of the family has been given a number (k1 value). The k1 values are calculated from the empirical formula k1 = ½ (E-V), where E = sum of octet electrons and V = sum of valence electrons in the cluster. This empirical formula has been discussed in our previous publications1-2. What is interesting about the empirical formula is that it predicts a quadruple bond for C2 diatomic molecule as found from high level theoretical calculation methods3-4.

ANALYSIS OF k1 VALUES

The k1 numbers do vary from family to family and also within the members of the same boron family. A movement from one family member to the next family member (horizontally, similar to a period in the periodic table), the k1 number varies by 1. On the other hand a movement from one member to the next member of the same family( similar to a group in the periodic table), the k1 number varies by 2. Clearly these are simple arithmetical series. The following examples illustrate this point.

been given a number (k1 value). The k1 values are calculated from the empirical formula k1 = ½ (E-V), where E = sum of octet electrons and V = sum of valence electrons in the cluster. This empirical formula has been discussed in our previous publications1-2. What is interesting about the empirical formula is that it predicts a quadruple bond for C2 diatomic molecule as found from high level theoretical calculation methods3-4.

Across families: B6H6(12), B6H8(11), B6H10(10), B6H12(9), B6H14(8); (simply add or subtract 2H atoms)and  across members of the same family: B5H7(9), B6H8(11), B7H9(13), B8H10(15), B9H11(17), B10H12(19), B11H13(21), B12H14(23)( simply add or subtract BH fragment). A large number of hypothetical neutral boranes expected from the formulas have never been synthesized. For instance, the neutral members of the closo family, B5H7, B6H8, B7H9, B8H10, B9H11, B10H12, B11H13, and B12H14 have not been observed instead B5H5⏋2―, B6H6⏋2―, B7H7⏋2―, B8H8⏋2―, B9H9⏋2―, B10H10⏋2―, B11H11⏋2―, and  B12H12⏋2―, are well known. In Table 1, it hasbeen  found easier to explain the series by assuming that all boranes are neutral. For instance to test to which family a hydroborane belongs, B2H7⏋― is regarded as B2H8 and B5H8⏋― as B5H9. A collection sample of boranes have been classified based on Table 1 and these are presented in Table 5.

DIAGONAL RELATIONSHIP WITHIN THE FAMILIES

The diagonal relationship within boranec families can readily be discerned from Table 1. The examples include  B5H7(9)→ B4H8(6)→ B3H9(3); and B6H8(11)→ B5H9(8)→ B4H10(5). This diagonal relationship also presented horizontally in Table 3, is cited widely  in form of shapes5 and is partially presented in Fig. 1. The k1 numbers vary by 3 units.  The diagonal relationship within boron  families when set up horizontally, another diagonal relationship is detected. The variations are given in Table 4. This relationship links up boranes with the same number of B atoms but different number of hydrogen atoms from different families. For instance, B5H7(9)(CLOSO)→ B5H9(8)(NIDO)→ B5H11(7)(ARACHNO). The k1values vary by 1 and therefore the shapes differ.It has also been found from theoretical studies by Yao and Hoffman6 that the boranes  B3H9 , B4H12 and B6H18  have some stability with B6H18 being the most stable. These boranes belong to the families, ARACHNO, HYPO, and P (see Table 1) respectively. Furthermore, theoretical calculations7 indicate that the boranesB4H2, B4H24,   B4H6, B4H8 and B4H10( belong to the families B,C, N, AR in the Table 1) are more stable than B4H, B4H3, B4H5, B4H7, and B4H9 which  do not belong to any of the families.

 

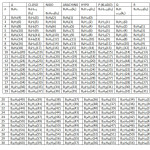Table 1: The k1 Values and the Borane Series Table1: The k1 Values and the Borane Series
Click here to View table

 

Table 2: Diagonal Relationship of k Values ofBoranes for n =2 to 12 Table2: Diagonal Relationship of k Values  ofBoranes for n =2 to 12 

Click here to View table

 

 Table 3: Geometrical Relationship corresponding to the Diagonal Relationship of k Values of Boranes Table3: Geometrical Relationship corresponding to the Diagonal Relationship of k Values of Boranes

Click here to View table

 

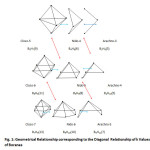 Fig. 1: Geometrical Relationship corresponding to the Diagonal Relationship of k Values of Boranes Fig1: Geometrical Relationship corresponding to the Diagonal  Relationship of k Values of Boranes 

Click here to View Figure

 

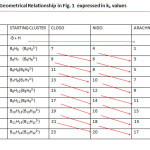Table 4: Geometrical Relationship in Fig. 1 expressed in k1 values Table4: Geometrical Relationship in Fig. 1  expressed in k1 values

Click here to View table

 

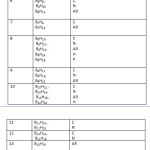Table 5 Table 5

Click here to View table

 

C = CLOSO, N = NIDO, AR = ARACHNO, H = HYPO, A = CLASS A, P = CLASS P,

Q = CLASS Q, R = CLASS R

Table 1Extended left wise

G F E D C0
n BnHn-10 BnHn-8 BnHn-6 BnHn-4 BnHn-2
1 0 0 0 0 0
2 0 0 0 0 B2
3 0 0 0 0 B3H
4 0 0 0 B4 B4H2
5 0 0 0 B5H B5H3
6 0 0 B6 B6H2 B6H4
7 0 0 B7H B7H3 B7H5
8 0 B8 B8H2 B8H4 B8H6
9 0 B9H B9H3 B9H5 B9H7
10 B10 B10H2 B10H4 B10H6 B10H8
11 B11H B11H3 B11H5 B11H7 B11H9
12 B12H2 B12H4 B12H6 B12H8 B12H10
13 B13H3 B13H5 B13H7 B13H9 B13H11
14 B14H4 B14H6 B14H8 B14H10 B14H12
15 B15H5 B15H7 B15H9 B15H11 B15H13
16 B16H6 B16H8 B16H10 B16H12 B16H14
17 B17H7 B17H9 B17H11 B17H13 B17H15
18 B18H8 B18H10 B18H12 B18H14 B18H16
19 B19H9 B19H11 B19H13 B19H15 B19H17
20 B20H10 B20H12 B20H14 B20H16 B20H18

 

Table 1 has been extended on the left to cover the boron families headed by symbols C0, D, E, and G. The whole Table 1 covers the series BnHn-10 to BnHn+14.

CONCLUSION

Borane series tend to occur in families just like hydrocarbons. The driving force for cluster formation is probably due to boranes attempting to obey the octet rule. A given borane that obeys the octet rule may be classified to belong to a particle family using the table. Both the known boranes and the theoretically established as being stable appear to fit into one of the families. Just as the elements of the periodic table follow a simple arithmetical progression, the boranes across the row horizontally (families- similar to the period in the periodic table)) and vertically( within the family members- similar to a group within the  periodic table) as well as diagonally (similar to the diagonal relationship of elements in the periodic table) follow simple arithmetical progression. The k1 values are useful in organizing the boron families and their members

REFERENCES

  1. Kiremire, E. M. R.Oriental J. Chem.2007,32(2), 809-812.
  2. Kiremire, E. M. R.;Kiremire, E. B. B. Materials Science Research India2007,4(1), 09-18.
  3. Shaik, S.;Danovich, D.; Wu, W.; Su, P.; Rzepa, S.; Hiberty, P. C. Nature2012 Chemistry, 4, 195-200.
  4. Su, P.; Wu, J.; Gu, J.; Wu, W.; Shaik, S.; Hiberty, P. C.  J. Chem. Theor. Comput. 2011,7, 121-130.
  5. Fox, M. A.; Wade, K. Pure Appl. Chem.2003, 75(9), 1315-1323.
  6. Yao, Y.; Hoffman, R. J. Am. Chem. Soc.,2011,133, 21002-21009.
  7. Böyükata, M.;özdoğana, C.; GÜvenç, Z. B.Romanian J. of Information Science and Technology200811(1), 59-70.

Creative Commons License
This work is licensed under a Creative Commons Attribution 4.0 International License.