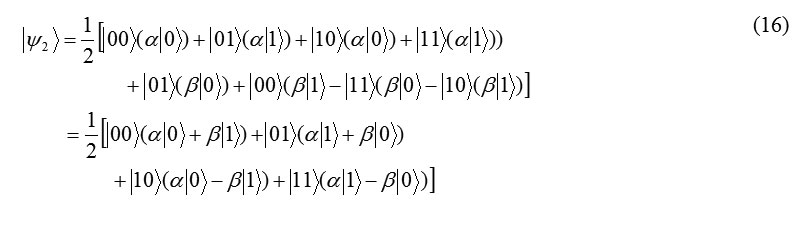Presentation Entanglement states and its application in quantum computation

Introduction

In quantum mechanics theory we can see the entanglement phenomena which are include two particles( photon or electron) in a separated space but their properties are related together in some way, at first this kind of system was interduced by Einstein_Podolski and Rosen( EPR)1-3 such as pair particle that each of them have spin1/2 and total zero spin that have anqular momentum total zero. The information(qubits) are transferred by intertwining phenomena of two objects quantum states. In other word entanglement phenomena of two objects quantum states can physically be in separated places, but have shared information ( qubits) in a same time. Before researchers had been succeed to intertwine the pairs of spin quantum states of electrons and the pair of spin quantum states of electrons and etc, by the way it is a unexpected and beyond conception phenomena in quantum theory mechanic.

Entanglement states

If we exert the following Git to the two qubit, the out let qubit is the result of the entanglementqubit.

Formula

 

 

Out let in up orbit for x=y=0 is the qubit state.

Formula

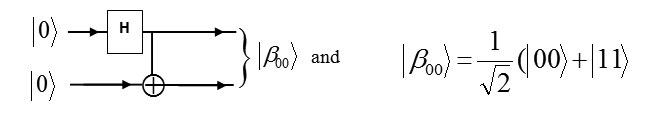
Calculation

FOrmula

 

 

This state can’t be shown by two isolate qubits; and there is a correlation between two qubits, the name of this qubits is entanglement. Even in so far distance this correlation between two qubits don’t be separated from each other.

This kind of correlation is known as John.Bell non-local correlation and it’s a response for Podox[batelnama] EPR .
The similar states of entanglement and correlation sates of two qubits that are known as EPR or BEL4-8 are

Formula

 

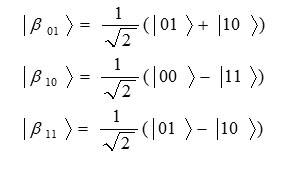
The simple model of quantum entanglement state

The mention the simple model of quantum entanglement state we can consider to a double electron system that just have spin. If we show the first spin with  and the second spin with , we can attribute a total spin S to the this system.

Formula

 

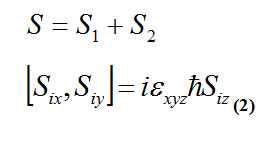
The total S size is achieved from following relation 9 .

Formula3,4

 

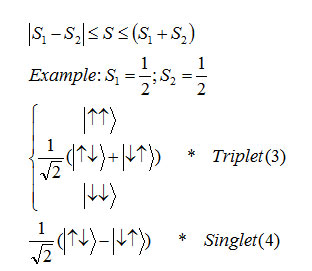
The bipartite quantum system ( tow qubit)

we can find the wonderful of quantum mechanic by checking the properties of two qubits quantum states. {|0>_A’|1>_A},{|0>_B’|1>_A}  are respectively the representation of orthonormal bases A and B, we image that two qubits quantum states is like the following form.

|ψ>_AB =a|0>_A  ⊗|0>_B +^b|1>_A ⊗|1>_B (5)⊗

In this case qubit A and B are correlate in regard to each other.

The measurement of qubit A by image on bases {|0>_A, |1>_B} with probability |a|² give the result |0>A and it makes appear the measurement of state of {|0>_B, }1>_B} and with probability |b|² give the results |1>_A and make appear the state of |0>_B ⊗ ^|1>_B ; so if we achieve the results of |1>_A, |0>_A, we can find the results |1>_B, |0>_B with insure (with one probability).similarly with measurement the qubit B we achieve the similar results. It mean the out lets of {|0>A , |1>_A} that come from measurements in |ψ>_AB  state are completed correlative.

It mean the outlets of  {|0>_A , |1>_A}, {|0>_B} that come from measurement in |ψ>_AB state are completely correlative.

Two qubits state |ψ>_AB  discussion is propounded for the bipartite quantum system ( Non division to two part).

Hilbert space of biparitite system H_A ⊗ H_B.

shown like total state in the pure state of bipartite can be shown like following form

Formula 6

 

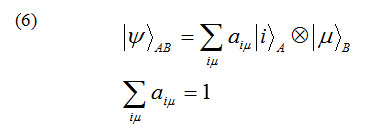
The physics model of entanglement qubit at pair production and pair annihilation:(Figure  1)

 

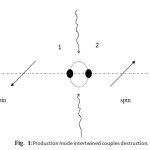Fig 1: Production mode intertwined couples destruction Click here to View Figure

 

4.Expectation value calculation of observable M_A on  |ψ>_AB  bipartite pure state 

by regard to observable as M_A ⊗ IA that MA operator itself is adjunctive that is exerted on A and IA  operator is unit is exerted on B.

Formula 7

 

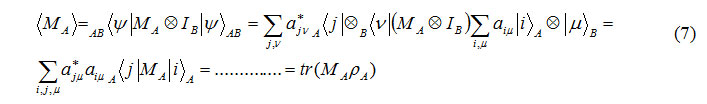
By regard to former calculations for single qubit and by regard to the following relation for matrix density we have.

Example

Formula 8

 

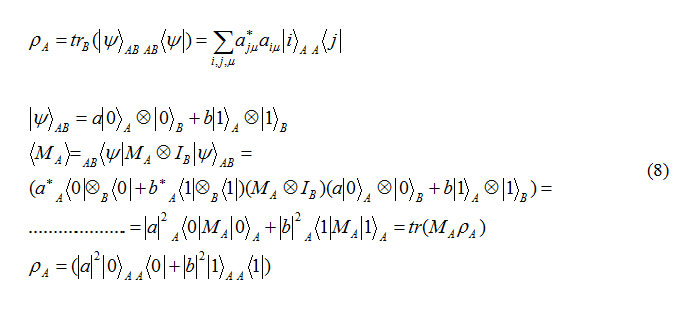
The applications of entanglement state 

In some methods that the intertwining process can lay for purpose of application use, we will consider to two cases of that ^10-12

Super-dense coding
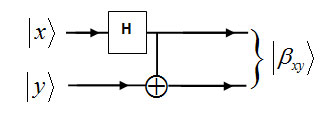
Let us assume that Alice at Amsterdam wants to send two bits of sending two separated bits. It is a question that can according to quantum mechanic theory for sending that, implement just by a single qubit? The answer is yes, in this field there are a lot of studies that coding the double bit classical massage in a pair of entanglementparticle( one qubit ). So on codition that Alice and Bob have been shared the qubit together at state of Bell(Figure 2), they say |β₀₀>

 

Fig 2: A pairofentangelmentqubitsarebelong toAlice and Bob, who sharethepremises ofa dense cloudencryptionis required Click here to View Figure

 

If this qubit that must be sent is 00 , as a result Alice simply would send her qubit to Bob that now have qubit in the state of |β₀₀>.

If a qubit which must be sent is 01, as a result Alice would use a quantum Git NOT X for her qubit ( assume that the first member of this pair in Bel state |β₀₁>  Alice similary use the suit transformation for her qubit. The consider qubits which must be sent, can be to the form of other combination from 10mand 11 that is sent to Bob.

The total result is that classical two bit xy would be coded by a single Bel state |βxy>. This kind of coding is created from a number of classical bits single entanglement quantum state, is known as a extremely mass coding. Where as four state of Bel are Orthonormal, consequently, certainly they are recognizable by a suitable measurement. So Bob can decode the qubitentanglement state that is in his hand and he can achieve the classical two bits information.(Figure   3)

 

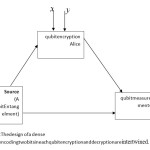Fig 3:Thedesign ofa dense cloudencoding two bitsineachqubitencryptionanddecryptionareintertwined Click here to View Figure

 

If the entanglementqubit be in the form of |β00> Alice will not do anything on that for sending that; But if two entanglementqubit be in other form like |β01>, |β10>, |β11> and Alice wants to send that to Bob, she must do the following actions for each one.

Formula 10,9,10

 

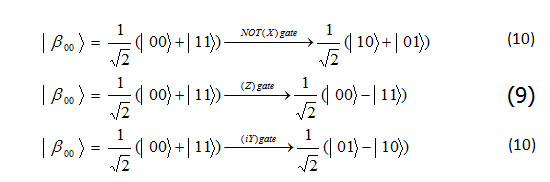
In this case, according to the (Figure  3) Alice would coding classical two bits in the entanglementqubit. Then Bob would decode by measurement on classical two bits qubit.

Let us assume that Alice and Bob are share in entanglementqubit of

formula

 

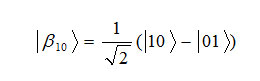
That the first qubitis for Alice and the second qubit is for Bob. If Bob achieve to qubit |0˃ by measurement on entanglement state, this mean is that he decode the classical Bit y=0 . and by knowing the entanglementqubit  could get a result that x=1, so with a measurement by Bob the classical bits in entanglementqubit would be decoding .

Quantum Teleportation

Alice in Amsterdam wants to send a desirable mono qubit |ψ>= a|0>+β|> to Bob in Boston. She can’t determine this state and send that information to Bob. Unless again we image that Alice and Bob have shared at a pair of intertwindqubits in one of the Bel state, such as

Formula 11

 

The qubit that must be sent with entanglementstate(pair) from far distance is started from three qubits state.

Formula 12

 

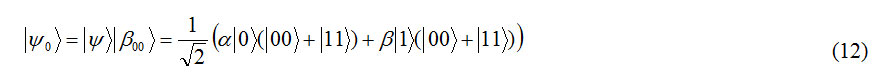
Here, normally, two firstqubit are in company with Alice and the third qubit is in company with Bob.

 

Fig 4:qubitquantum circuitforalighttherapy: Click here to View Figure

 

Now Alice lay her two qubit throughout a quantum git C-NOT. This process capture the qubit that must be sent from far distance in company with a part of entanglement state which is belong to Alice and it would pair them.
Of course this entanglement state is captured for creating and starting the work. As a result this three qubits in the state of captured (entanglement) would end to:

Formula 13

 

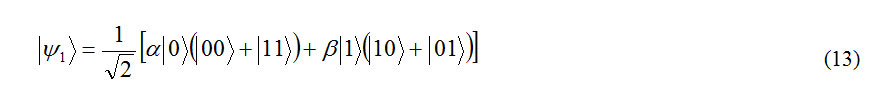
With regard to mentioned models in (1-3-8-1) and (2-3-8-1) the up word relation is achieved.

Then Alice would send the first qubit in throughout a Hadamardgit and we have our two qubits of calculation with application of Hadamardgit on qubit |ψ> :

Formula14,15

 

 

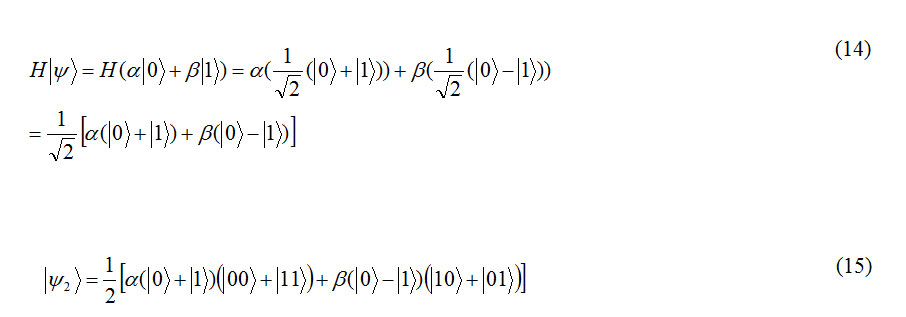
With a simple Tensory product operation and transfer the coefficient a, β  to the third qubit we have:

Formula 16

 

So, the result of Alice’s measurement with probability of 1/4 will be one of the pairs 11,10,01,00 and the state that is according to that in each Bob’s gubits that will be in left side is like this from:

Formula 17,18,19,20

 

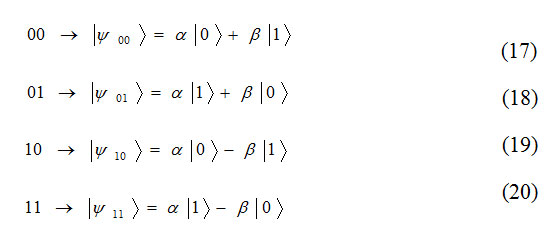
Now if Alice say her result to Bob (on a classical chanel like telephone or email or a quantum chanel like so mass coding), Bob will understand the circumstance of deformation and his qubit state transformation to |ψ> . If the result is 00, Bob will not do anything, because now he is in |ψ> state. For other probability results, Bob must use a suitable combination of Z and X . If the result be , so the total result will be like this from(Figure  5).

 

Fig.5:After the announcement of two classic albits Aliceand Bobchoose the appropriate gate qubit will receive  Click here to View Figure

 

For example : if Alice achieve the qubit  |ψ₀₁> in her measurement, by sending a massage to Bob (classical two bit) she will inform him that a qubit that is sent to him is |ψ₀₁> = a}1> +β|0

Formula 21

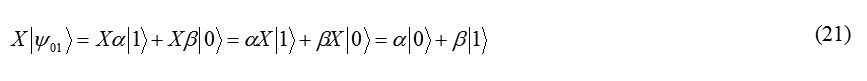
It’s like a magic in quantum mechanic. By the way this problem have been achieved practically at laboratory by sending a ray or photon light from one room to another room. There is a point.

Sending process from far distance don’t contradict the noclonictheory.i.e. copy of a desirable unknown state don’t be accomplished, but the main state  in current process would have a little deformation.
Sending process from far distance don’t contradict the special relativity theory, in this basis inevitable the practical information physically establish connection with a speed that is less than light.

Conclusion

Intertwining is one of the sources of establishment of secret quantum connections. This phenomena say that if two bits entanglement with each other, if they be far a from each other even millions kilometers and upon one of we perform the measurement process, at that moment we can achieve the information of the second bit. They have effect on each other, i.e. higher than light speed and immediately! Einstein called this subject as a ghostly process in far distance that is like to a connection between two entanglement pieces by invisible wires which we don’t have any information from them, but it is a total principle for quantum computations. Scientists like Einstein, Podloski and Rosen introduced the EPR theory.

Surprising phenomena of intertwining in quantum mechanic theory made a big evolution in quantum theory and also in quantum computers; inaddition to mentioned applications in this chapter, intertwining phenomena has a so attractive application in quantum computers i.e. it has a secret quantum key distribution that its importance is not secret ton anyone. One of the so important result of intertwining phenomena is that it contradict the locality and it proved that the nature of quantum mechanic theory is non-local.

References

1. J.Perskill.2001.Lecture notes for Ph219/CS219: Chapter 4, Quantum Information and computation.
2. G. Auletta. 2001. Foundations and Interpretation of quantum mechanics. World scientific, Singapore. New Jersey. London. Hong Kong, PP.531-544.
3. A.Prers. 2002. Quantum Theory: Concepts and methods.Kluwer Academic publishers, Newyork, Boston, London, Moscow, pp.148-155.
4. Sara M.McMurry.1993-94. Quantum Mechanics, pp.337-346.
5. A.zeilinger.1997. A Fundamental Concept Finding its Applications, PP.12-18.C.Macchiavello, G.M.Palma, A.zeilinger.1999. , Quantum computation and Quantum Information.ISBN 981-02-4117-8.World scientific, Singapore. New Jersey. London. Hong Kong.
6. G. Auletta. 2001. Foundations and Interpretation of quantum mechanics. World scientific, Singapore. New Jersey. London. Hong Kong, PP.42-44.
7. G. Auletta. 2001. Foundations and Interpretation of quantum mechanics. World scientific, Singapore. New Jersey. London. Hong Kong, PP.583-585.
8. J.Perskill.2001.Lecture notes for Ph219/CS219: Chapter 2, Foundations I: State and Ensembles.
9. J.J. Sakurai. 1982. Modern Quantum Mechanics.
10. A.Chatterjee.2003. Introduction to quantum computation.quant-ph/0312111.
11. G. Auletta. 2001. Foundations and Interpretation of quantum mechanics. World scientific, Singapore. New Jersey. London. Hong Kong, PP.743-755.
12. Michael a. Neilson, and Isaac L. Chuang 2003. Quantum computation and Quantum Information.World scientific, Singapore, PP.26-28.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.