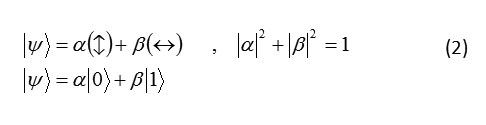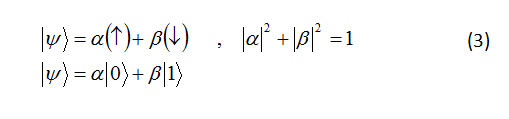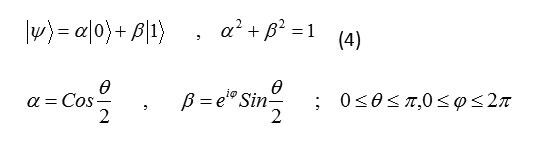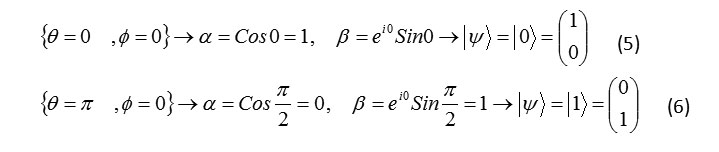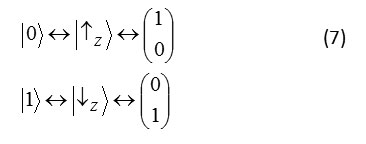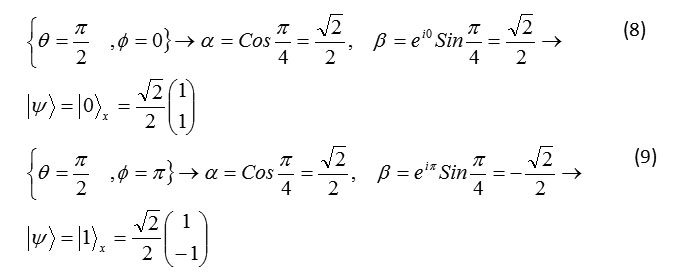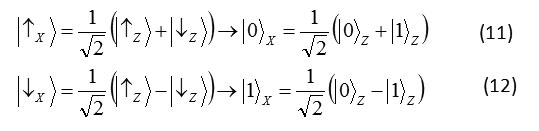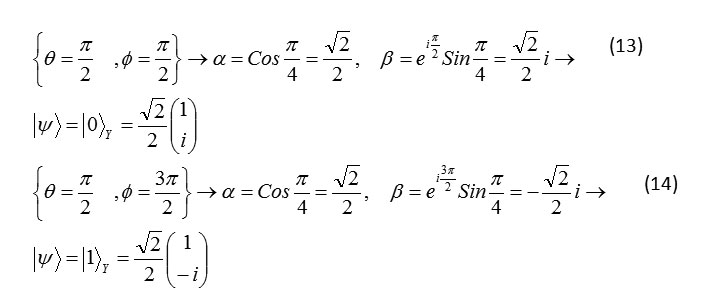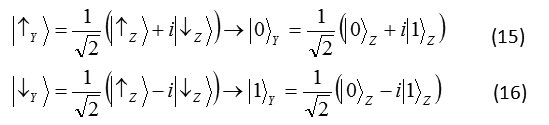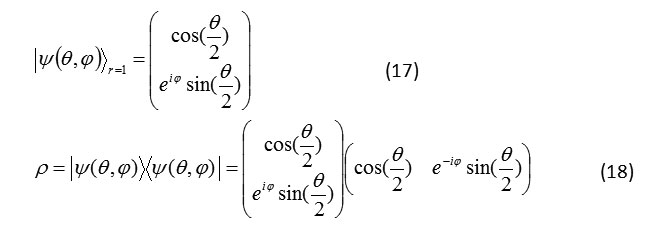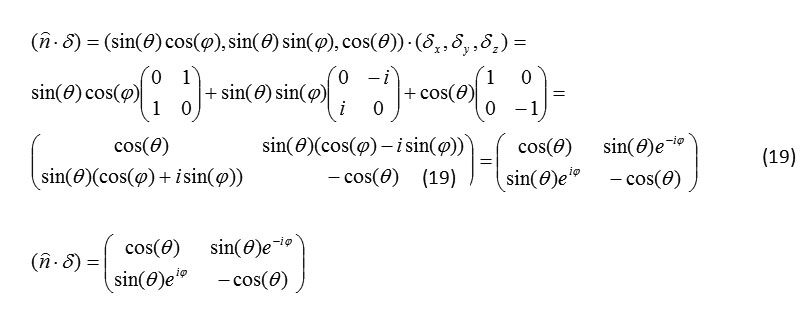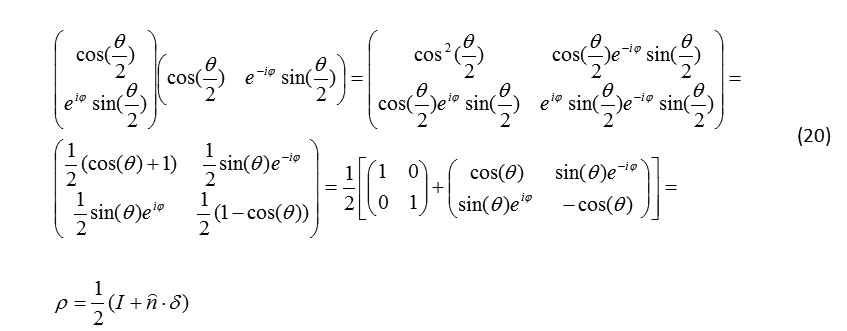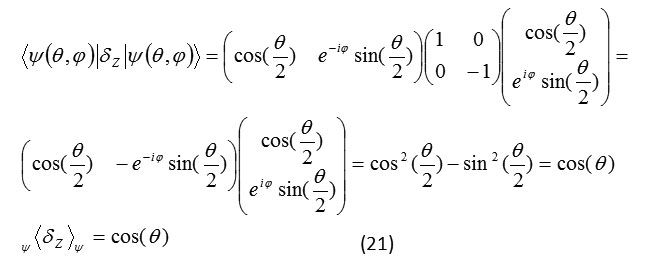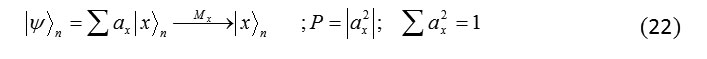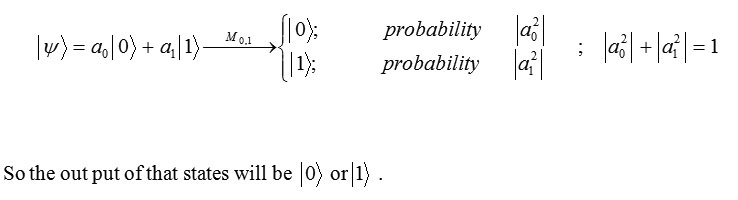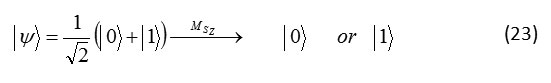A Study of Quantum Information and Quantum Computers

INTRODUCTION

a way that can be used to transfer the quantum information from the quantum states such as linear polarization and rounded photon , electron spin or neutron and etc , can be used for making the in penetrable global information networks and the computers which work with a amazing speed. Making information between quantum memories(quantum states) , is necessary for making complicate network that use from quantum phenomena ( like intertwining and superposition ). Though quantum networks are so suitable for making safe information and high speed calculations but quantum states of information carrier are so sensitive in regard to interference so they can be used for making the connectional channels of quantum for optical path . this channels has the capability of making a completely impermeable connection , because any effort  for information achievement by overhearing , lead to disturb of quantum cultur of delivery data…before this way can be used for the applied alms , we need more theorical development in this ground, in this article we will proceed to examine the quantum states which have capability to be used for making complex quantum network, then by using from a model quantum states such as quantum states of particles spin(electron) we will proceed to primary and main structure of a quantum computer .

by using from quantum theory we will introduce each of quantum states by quantum bits and we will examine their dynamical transformation and we will introduce quantum git and we will examine their operation in quantum computers.

 The quantum computers in the case of practical realization can out do from the best modern computers , in quantum world there are phenomena in a different and amazing kind ,so using them in making quantum computers is suitable for information processing.

Engineers that design the quantum computers and the expect of mechanic quantum hope that use from one of the most basic quantum theories principles for design of systems (machines) that are able to do parallel computation concurrently , this computations provide the possibility of easy and logical solution of some of the problems that are insoluble in classical computers and also this computations provide the extant difficulty in the ground of cryptography.

The memory of a quantum computer is a quantum states , quantum computers are mode from qubits . qubits can have zero bit and one bit concurrently i.e. they are equivalent with superposition of classical bits. So quantum states can be consider as quantum computers bits. In regard to that quantum states are mode from  phenomena of quantum mechanic , so computations of quantum computer are found on the base of physics process and quantum principles.
Qubit is the smallest part of the a system (memory unit) in quantum computers that is analog bit in classical computers. Each quantum state that is superposition ι 0>of and ι 1> states an be considered as qubit, in math language we have

Formula 1

 

 

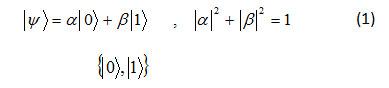
.(Are the bases of the smallest Hilbert space ( tow dimensional

In regard to the condition of norm there are a number of infinitly  amounts for   and infinitly concurrently states for qubit  the main work of quantum computers are in a way that can process concurrently the qubits that are include infinitly state. In the baseon basic principles of quantum mechanics theory ,a qubit can has zero state and one state concurrently , so it is possible that a qubit take a part in more >do a lot of parallel computation.

Here the main note is that making a quantum computer is so difficult, nevertheless there is a new step toward that. In a quantum computer instead of using from transistors and normal computer circuits is used from atoms and other micro- articles for information processing. A bit can at as a memory bit in computer and information

The primal model of quantum computer that is mode , its main part is a calcium atom in the base on energy levels and a program have been done by this computer. Another model is cadmium that in the same moment can be settled in both internal quantum  state, both one and zero.

There are many design for the manner of making quantum computes and also there will be many other design. It is possible that , be from a qubit of ground state and exited of a bit or it is possible the ι 0>, ι 1> polarizasion of photons Or even it is possible that they are more that one state of bit spin 1-4.

qubits introduce in different quantum states

There are different quantum states in quantum theory that can be used as qubits in quantum computers i.e. by behavior simulation of quantum states from each physics system in quantum mechanics theory , we can from the filament of qubits that we will point to them

Photon

A – the linear polarization of photon for example in direction of (↔) x or (↕) z that are the quantum states of photon linear polarization be consider and respectively qubit and attribute to them.
So each photon can be in each direction in the plane xz to the from of superposition of linear polarization.

Formua 2

 

 

 

 

B-  rounded polarization of photon can be used similarly in the main structure of quantum computers in regard to quantum state of photon polarization of anticlockwise and clockwise respectively by qubit ι 0> and |1>.

The electron spin in the up and down  direction is shown by quantum state |↑>, |↓> that respectively qubit  and   can attribute to them. In regard to theory principles of spin quantum mechanics each electron can has the following superposition from spin quantum state.

Formula 3

 

 

Atom

In the main structure of quantum computers we can use from internal states of a atom i.e. ground stat |g> and excited state

|e> for showing the qubits |o> and |1> .

 

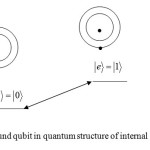Fig 1 : ground qubit in quantum structure of internal states of atom Click here to View Figure

 

Dot quantum

Also energy levels in atoms like previous cases can have qubits according to the following figure and can be used in the main structure of quantum computers.

 

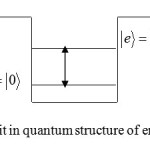Fig 2 : ground qubit in quantum structure of energy levels of atom Click here to View Figure

 

so until while that there is a way to set a system in a quantum superposition state and also until while that there is a way for matual inter ference of qubits, this system potentially can be used as a quantum computer. ^5,6

Mover bits of quantum information carrier have the ability of kilometers marching.

Consequently it id possible to establish quantum connection from so far distance.

In spite of this the only problem in quantum computer is the way of work with qubits

Adjustment of primary values is difficult for them and so reading the result is not easy too. When the computations are being done , it is necessary that various qubits impress or each other in a suitable and controlled method and it is in a time that system must be completely isoleh toward external in vironment .

The most popular example of power of quantum computers is the olgorithm of peter shor for analysis of big numbers. On important problem in cry photography is the number analysis to the first factors , for example the security of coding the general key , RSA is depend on the first factors, in spit of many researches it has not known an efficient classical computation olgorithm for that.

In fact shor solved this problem and fortunately there is effective quantum olgorithm for this transformation .

Bolch sphere representation

Bolch used from a sphere with unit radius that are shown the angle  points on sphere. Opposite (Figure 3)and the following connection are known.

 

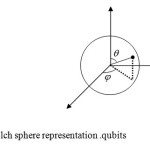Fig 3: Bolch sphere representation .qubits : Click here to View Figure

 

Formula 4

 

 

qubit representation in north pole and south pole of Bolch sphere

Formula 5,6

 

 

 

Qubit is a state in two dimension Hilbert space that can be any state in the form of |ψ>=a|0>+β |1> in normalizing condition

a² +β² = 1 in regard to up state can consider the state of bit spin ground (electron …) in direction of z axis as ground states of a qubit .
Ground state S_z

Formula 7

 

 

Qubit Representation in direction of x axis

Formula 8,9

 

 

The state ground   itself is superposition from state of ground   and it is expressed as qubit according to following equation.

Formula 11,12

 

 

Qubit Representation in direction of y axis

Formula 13,14

 

 

State ground S_Y

Formula 15,16

 

 

 

So we can see the representation of an1y qubit such as s1 in Bloch sphere 7.

Density matrix of qubit in regard to Bloch sphere representation

Density matrix for any quantum state is according to the following relation ⁸.

Formula 17,18

 

 

For any unit rector in ideal direction upon Bloch sphere ñ

 

Fig 4: representationfor any unit rector in ideal direction: Click here to View Figure

 

Formula 19

 

 

Formula 20

 

 

 

Expected value qubit in direction of z axis⁹

Formula 21

 

 

Measurement of qubit

If we measure the state of |ψ>

Formula 22

 

For example

Formula

Formula 23

 

 

collapses( reduction)of quantum state

Measurement of S_z a qubit would result to collapse to one of the ground states of S_z i.e. |0>and |1>. Here we would check the measurement process in the system of unit qubit and two qubit.

A-if we have a unit bit system with spin 1/2 in state of |ψ>, then

Formula 24

 

After measurement, qubit will collapse to one of the main states with possibility equal 1/2 In state of   B-if a two qubit system that each of them has spin 1/2 in state of | ψ>

After measurement , the qubit would be collapsed to another main states with possibility of equal 1/2.

The measurement operation has vole in creating new external state , and when measurement occure that the measurement set do with interaction system

In fact , the most reaction that are in environment , such as a measurement operation  are coused to collapse of quantum state. The world in a continuous human scale are collapsing the superposition to the more classical states, this current is reversion to the classical state.if we want to keep a quantum state , for a while , without doing any computation , and or if we want to send that by a normal channel which has parasite (noise) , the computation of quantum state must be perfect. And it is a big problem for a quantum computer , if we cant stop it from reaction (action and reaction ) with environment , we would not have better than a classical computer. It is clear that the stop problem is a problem like prevention from general parameter. The solution of this problem is using from the code of quantum error correction .

The simplest code of the classical error correction id the repetition code , we make zero to the code of ooo and we make one to the code of 111 , then if it wove even a little (i.e.do interaction with environment) it may we reach to the state of 011: and we can return that by the error correction code that is the main state of 111.¹⁰

CONCLUSION

Resently the theorist physicists could express the structure of quantum computers (qubits) in the various from in the base on theory or mechanic principles that we considered that in this article and the done computation show that qubits are the behavior of quantum states from each physics system in quantum theory. It is a evalution in information science and computers , among them provide the expectation of security connection system, the fast process and the various computations.

Offers

Today there are many interesting achievement in the ground of quantum computation and technology the is related to that .the conditions and prerequisites that are related to quantum hardware are expressed simply , in such a manner that is so necessary practically . firstly a multiple recorder that is related to quantum qubits must be provided in a writeable from, and must be away from the environment

Effects that bring about damage and decoherence of quantum states.Secondly , in spite of a weak connection to the external world , the qubits must be connection together by a external control mechanism in purpose of doing operation in logical gate .  thirdly , it is necessary to exist a way of reading for determine of state of each qubit in the end of computation.

Reference

1. D, Mermin., Lecture notes on Quantum Computation., I. Fundamental .(2005).
2. A,Chatterjee., Introduction to quantum computation.quant-ph/0312111. (2003).
3. Michael a, Neilson., Isaac L,Chuang., Quantum computation . (2003).
4. A, Ekert., Introduction and over view. (2004).
5. J,Perskill.,Lecture notes for Ph219/CS219: Chapter 1., Introduction and over view.( 2001).
6. G, Auletta. , Foundations and Interpretation of quantum mechanics. World scientific, Singapore. New Jersey. London. Hong Kong, PP.759-781. (2001).
7. J,Perskill., Lecture notes for Ph219/CS219: Chapter 4, Quantum Information and computation.( 2001).
8. G,Auletta., Foundations and Interpretation of quantum mechanics. World scientific, Singapore. New Jersey. London. Hong Kong, PP.40-42.( 2001.).
9. G, Auletta. , Foundations and Interpretation of quantum mechanics. World scientific, Singapore. New Jersey. London. Hong Kong, PP.51-53.( 2001).
10. D,Mermin., Lecture notes on Quantum Computation: III. Quantum error correction. Physics 481-681,CS 483. (2005).

---

This work is licensed under a Creative Commons Attribution 4.0 International License.