Study of Effect of Variation of Ionic Strength of the Medium on Velocity Constant of Ru(Iii) Catalyzed Oxidation of Hydroxy Benzoic Acids by Chloramine-T in Acidic Medium

INTRODUCTION

IONIC STRENGTH

The rate of reaction between charged species are affected strongly by the ionic strength of the solution, which is defined as: –   

I         = ½ S c_i Z_i²

where c_i is the concentration of each ion present in the solution and Z_i is its charge number. When the reacting species are of the same sign, an increase in ionic strength increases the rate, when ions of opposite signs react, there is a decrease in rate with increasing ionic strength Bronsted, Bjerrum, Christiansen, Davis and Scatchard suggested that the rate of reaction between species A and B should be expressed as –

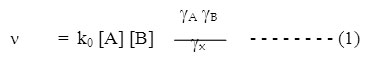
where k₀ is a constant at a given temperature, g_A and g_B are the activity coefficient of the reactant and g_x is collision complex. According to Debye-Huckel theory, the activity coefficient g_i of an ion is related to the ionic strength by the equation –

where z_i is the charge number of the ion and B is a quantity, whose value can be calculated from Debye-Huckel equation. From equation (1) the rate constant k (=v//[A] [B]) is –

which is logarithmic form including equation (2) becomes-

For an aqueous solution at 25⁰C this equation becomes –

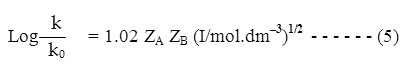
According to equation (5) a plot of log k versus   (I/mol. dm^–3)^1/2 will give a straight line of slope 1.02 Z_AZ_B and intercept is log k₀. If one of the reactants is a neutral molecule, Z_AZ_B is zero and the rate constant is expected to be independent of the ionic strength. The rate constant of a reaction between an ion and a neutral molecule should vary with the first power of the ionic strength instead of with the square root. k = k₀ (1+bI) so the rate constant should vary linearly with I.

Chloramine-T is the sodium derivative  of  N-chloro         p-toluene sulphonamide CH₃C₆H₄SO₂NClNa.3H₂O (molecular weight 281.70), prepared easily and mainly from p-toluene sulphonic acid, a cheap by product in the manufacture of saccharin. It is a less familiar but very potent oxidizing agent in alkaline as well as in acid media. A survey of existing literature showed that chloramine-T has been used for the determination of numerous inorganic and organic substances. It has been reported that in acidic medium (Hydrochloric acid), [RuCl₆]^–3 is taken as reactive species. For the sake of simplicity, [RuCl₆]^–3 is written as [Ru(III)] in the same scheme. Ru(III) chloride exists as [Ru(H₂O)₆]³⁺ in dil. HCl. Such type of aqueous complexes are known to exist in the form [Ru(H₂O)₅OH]²⁺ in equilibrium with hexa aquo form.

[RuCl₆]^–3 which is in equilibrium with [Ru(H₂O)₅OH]^–2 in the following manner.

 

This equilibrium in right direction would be highly favoured in acidic medium, suggesting that [RuCl₅.H₂O]^2– in the actual reactive species of Ruthenium (III) chloride in present work.

EXPERIMENTAL

To determine the effect of variation of Ionic strength of velocity content of Ru(III) Catalysed oxidation of hydroxyl benzoic acid the various experiments with varying ionic strength (affected by addition of suitable amount of sodium perchlorate) at constant concentration of other reactants have been carried out in oxidation of each hydroxyl benzoic acid and the result have been reported in table A,B and C respectively in ortho- hydroxy benzoic acid, meta- hydroxy benzoic acid, para-hydroxy benzoic acid in a summarized way.

 

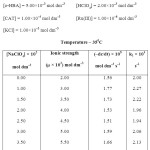TABLE – A Click here to View table

 

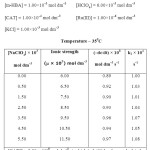TABLE – B  Click here to View table

 

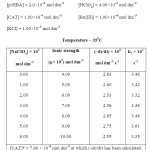TABLE – C Click here to View table

 

CONCLUSION:

It is clear from the result of the tables A, B & C that upon increasing the concentration of sodium perchlorate, the ionic strength variation does not change the reaction velocity constants significantly. Thus there is negligence effect of ionic strength of the medium on reaction.

REFERENCES 

1. F. Pearson, Kinetics and Mechanism, 2^nd Edn
2. J.N. Bronsted, Z. Phys. Chem., 102, 169 (1922).
3. J.N. Brosted, J. Am. Chem. Soc., 49, 435 (1937).
4. N. Bjerrum, Z. Physik. Chem., 108, 82 (1924); 118, 251 (1925).
5. J.A. Christiansen, Z. Phys. Chem., 108, 82 (1924).
6. F.A. Cotton and G. Wilkinson, “Adanced Inorganic Chemistry”, Wiley, New York, 2^nd Edn., p. 152 (1966).
7. R.E. Connick and D.A. Fins, J. Am. Chem. Soc., 83, 3474 (1961), 82, 4187 (1960)..
8. H.H. Cady and R.E. Connick, J. Am. Chem. Soc., 80, 2646 (1958).
9. J.R. Backhours, F.D. Doyer and N. Shales, Proc. Roy Soc., 83, 146 (1950).
10. J.C. Morris, J.A. Salazar and M.A. Winemann, J. Am. Chem. Soc., 70, 2036 (1948).
11. F.E. Hardy and J.P. Johnston, J. Chem. Soc., Perkin-II,  642 (1973).
12. Y.K. Gupta and K.S. Gupta, J. Chem. Educ., 61, 972 (1984).
13. H.S. Yathirajan, D.S. Mahadevappa and Rangaswamy, Talanta, 27, 52-54 (1980).
14. A.I. Vogal, In quantitative organic analysis (Part 3) (ELBS, Longman, London), 739 (1958).
15. G.C. Amin, S.D. Wadekar and H.U. Mehta, Ind. J. Tex. Res., 2, 20 (1997).

---

This work is licensed under a Creative Commons Attribution 4.0 International License.