Kinetics of Isothermal Annealing of Gamma-irradiation Damage in Thallous Nitrate

INTRODUCTION

The effects produced in solids by bombardment depend on nature of the target and energy of the incident radiation. The important effects are excitation, ionisation, atomic displacement from lattice sites and transmutation of nuclei which are either primary or secondary depending on the sequence of the events following the absorption of energy^1-3. The primary effect of neutron irradiation is atomic displacement with ionisation as a secondary process. On the other hand, irradiation with γ-rays produces ionisation as the important primary effect, atomic displacements sometimes results secondarily^4-6.

The chemical damage induced in systems containing oxyanions, such as nitrates, bromates, chlorates and perchlorates has been reviewed by Zakharov and Novostruev⁷ and by Johnson⁸. The stability of radiolytic product varies widely with crystal matrix⁹. It was observed by Maddock and Mohanty¹⁰ that macroscopic chemical damage induced by energetic radiations is susceptible to recovery (annealing) in the same way as microscopic chemical effects of nuclear transformations and physical effects of irradiation. They observed that when radiolysed solid metal nitrates are heated the damage nitrite diminishes progressively with time. The disappearance of the nitrite was due to the recombination of the damage fragments which remain trapped in the lattice to form the original nitrate. Following this, several research groups^11-18 have studied the radiolysis and recovery of damage fragments in irradiated nitrates of alkali and alkaline earth metals as well as complex compounds. The extent of annealing may differ from system to system depending on the physical and chemical properties of the host crystals and upon that of the irradiation employed⁹.

In the case of irradiated metallic nitrates which show crystal transformations on heating, the recovery processes are taking place due to thermal reactions as well as reactions accompanying phase transformations in the damaged crystals¹⁹.  It was reported²⁰ that the yield of both the nitrite and oxygen formed by the radiolysis of potassium nitrate was reduced by post irradiation heating of the nitrate above the phase transition temperature (rhombic→trigonal at 402 K). It was observed by Clark and Reinhardt²¹ that TlNO₃ shows two crystal transformations on heating. When heated to about 350 K the orthorhombic crystals transform into a rhombohedral form, which in turn changes to cubic at 418 K. So it is of interest to investigate the effect of γ–irradiation and subsequent isothermal annealing of chemical radiation damage in TlNO₃ at different temperatures in the range 393-433 K. This has been carried out with a view to determine the order of the recovery process and  the energy of activation on the basis of diffusion controlled mechanisms^{22, 23} as well as Conventional chemical kinetic methods²⁴.

EXPERIMENTAL

Irradiation

Analytical reagent grade TlNO₃ (Sigma-Aldrich) was used. The sample was sieved to obtain crystals in the 85-100 mesh range. Samples of TlNO₃ sealed in glass ampoules were irradiated at room temperature with ⁶⁰Co γ -rays to a dose of 7×10² KGy at a dose rate of  2 KGy h^-1. The irradiated samples were thoroughly mixed and stored over phosphorus pentoxide.

Analytical procedure

The damage nitrite was estimated spectrophotometrically by the method developed by Shinn²⁵ and modified by Kershaw and Chamberlin²⁶. The method was shown to be sensitive to 3 ppm of nitrite. The colour was found permanent up to 70 min after development.

In the routine measurements, 0.2-0.3 g of the irradiated nitrate crystals were dissolved in boiled out distilled water to give 100 mL of solution.  A suitable aliquot of this solution was transferred to a 50 mL standard flask and 2 mL of a 0.5 % solution of sulphanilamide in 1:1 hydrochloric acid added. After 3 min, 1 mL of a 0.1 % solution of N-(1-naphthyl) ethylenediamine dihydrochloride was added. After mixing, the solution was made up to 50 mL and allowed to stand 15 min before measurement of the absorbance at 540 nm.

FT-IR spectrum

The FT-IR spectrum of both untreated and irradiated TlNO₃ was recorded on KBr pellets using Schimadzu spectrophotometer.

TG/DTA analysis

Thermogravimetric (TG) and differential thermal analysis (DTA) of untreated TlNO₃ was performed on an SII NanoTechnology TG/DTA 6200 instrument with pure nitrogen (50 mL min^-1) as a carrier gas at a heating rate of 5 °C min^-1 using aluminium crucible.

Thermal annealing

Isothermal annealing runs were made with the irradiated crystals in air for different time intervals up to 20 h at various temperatures in the range 393-433 K and also at a temperature 343 K (below phase transition temperature) in a thermostatic electric hot-air oven maintained to within ±1 ⁰C of the desired temperature.

RESULTS AND DISCUSSION

IR spectral studies

FT-IR spectra of untreated and irradiated TlNO₃ are depicted in Figure.2. An intense and wide peak centered at ~1364 cm^-1 (Figure 2a) is due to asymmetric stretching vibrations of NO₃^– ion. The peak at 1044 cm^-1 is attributed to symmetric stretching vibrations of NO₃^– ion. The asymmetric and symmetric bending of NO₃^– appears at 820 and 711 cm^-1 respectively.

It has been already reported that inorganic nitrate and nitrite groups show four and three fundamental modes of vibrations, respectively, in IR region^27-30. Nitrate has four modes of vibrations at 1370, 1020, 840 and 730 cm^-1, but only two characteristic bands are observed in the vicinity of 1380-1350 and 840-815 cm^-1. In another article³¹ it is reported that asymmetric and symmetric stretching of Free State of NO₃^– occurs at 1355, 1049 cm^-1 respectively whereas the asymmetric and symmetric bending of NO₃^– appears around at 830, 690 cm^-1 respectively. A comparison of FT-IR spectra of un-irradiated and irradiated TlNO₃ shows that spectral region of 1500-1000 cm^-1 for irradiated samples have some changes in frequency and intensity of vibrational bands. This difference essentially arises due to the interactions between the vibrations of NO₃^– and NO₂^– ions in the lattice. This clearly provides additional evidence besides spectrophotometric estimation, for the formation of NO₂^– ions formed upon γ-irradiation on TlNO₃. The observed change in pattern of FT-IR spectrum in the spectral region 1000-1500 cm^-1 for untreated and irradiated TlNO₃ in the present work (Figure 2) is similar to that reported for γ-irradiated Ba(NO₃)₂³².

TG/DTA curves

Figure 2 shows TG/DTA curves for untreated TlNO₃. Two solid-solid transition points and the melting point observed from DTA curve are 350 K, 420 K and 481 K, respectively. TG showed a weight loss beginning at ~ 663 K with a 50 percent loss by ~ 793 K. This weight loss was demonstrated to be caused by boiling rather than decomposition. The DTA extrapolated onset temperature for the boiling was 719 K. The similar observations have been reported earlier for the TG/DTA study of TlNO₃ by Clark and Reinhardt²¹.

Isothermal annealing curves

The irradiation produced a golden yellow coloration in the crystals. The initial damage produced by 7×10² KGy of ⁶⁰Co γ-rays in TlNO₃ was 1386 ppm of nitrite. The bleaching of the colour produced and the recovery of damage upon heating of the irradiated crystals were similar to those reported earlier^{24, 18}.

The fraction annealed φ in terms of nitrite concentration on heating the irradiated sample at a given temperature is given by:

where [NO₂^–] ₀ and  [NO₂^–] _t are the values of nitrite concentration at initial and after a time t respectively at a given temperature.  The annealing pattern for damaged nitrite in TlNO₃ at various temperatures in the range 393-433 K and also at 343 K is presented in Figure 3. The recovery of damage below phase transition temperature is very slow as shown by the curve at 343 K. But the fraction annealed φ, in the range 393-433 K first increases rapidly and then slowly with heating time, t. This abrupt recovery of damage is due to thermal reactions as well as reactions accompanying phase transformations as reported earlier^{33, 34, 19} in the damaged crystals.

Kinetics of isothermal annealing

In order to determine the order and the energy of activation for the recovery process of γ-irradiation damage in TlNO₃, the annealing data has been analysed using three different kinetic methods: Flethcher and Brown, Waite and Conventional chemical kinetic methods. The details of these methods have already been reported^{11, 16, 17}.

The Fletcher-Brown model

Fletcher and Brown²² and Brown et al.³⁵ have considered the theoretical aspects of recombination. According to Fletcher and Brown, the recombination occurs in three stages, viz., close pair, liberation and second order, and it is governed by a single energy of activation so that recovery is a unique function of equivalent time, t^’.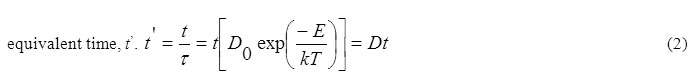

where τ = 1/D = D₀^-1exp(E/kT), the diffusive jump time in the lattice, t the heating time, t^’ the equivalent time, D₀ the constant frequency term, E the energy of activation formation, k the Boltzmann constant, T the heating temperature, and D the diffusion coefficient. Since the annealing is a function of t/τ only, it is possible that data at different temperatures and time intervals can be adequately superimposed on to a single universal curve by adjusting the time scales by proper factors. The application of Fletcher and Brown model to our data for the annealing reactions in γ-irradiated TlNO₃ is shown in Figure 4 in which the data are plotted against logarithm of equivalent time at a reference temperature of 413 K. The data are adequately superimposed and are represented by the continuous curve which is the theoretical fit of the following combination of a fast first order and a slow predominant second order process:

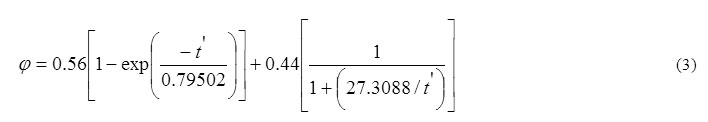
The logarithm of the relative jump time τ_{(413 k)}/ τ_(T) is linearly related to 1/T (Figure 5), and the activation energy computed is 19.7 k cal mol^-1.

The Waite model

Waite has treated the entire phenomenon of recovery as diffusion limited reaction. The resulting expression for the kinetics of recovery is very complex, but for small initial defect concentrations and for early times:

where γ is the fraction of the damage annealed at time t, D the diffusion coefficient and K a quantity independent of temperature. The change ofφ/t^1/2 for early times with temperature gives the temperature dependence of D, which is of the form:

In this case, the recombination is governed by a single energy of activation, as in the case of Fletcher-Brown model. The Waite plots for annealing of irradiation damage in TlNO₃ at different temperatures are shown in Figure 6, as a graph of φ against t^1/2. It is seen that the curves are linear for early times in agreement with the Waite theory. The activation energy for diffusion is calculated from the temperature dependence of φ/t^1/2 as 21.2  k cal mol^-1 (Figure 5), and this value is comparable to that obtained in the Fletcher-Brown treatment of the data. Figure 7 shows that the annealing data taken at different temperatures can be represented by single universal curve, by a proper adjustment of the time factor, as a unique function of [D₀ exp(-E/RT)t]^1/2 so that the data are adequately superimposed in this universal curve. The initial linearity of this curve is also evident from Figure 7, in agreement with the Waite theory.

 Analysis on the basis of conventional chemical kinetics

The  annealing  data  have also  been  considered  in  the light  of Conventional chemical kinetics and  is found that  plots  of the  reciprocal  of the nitrite concentrations are a function of time (Figure 8).  The linear  portions  of the  curves do not  extrapolate to the  same intercept on the t = 0 axis because with rise  in  temperature,  lattice  mobility increases, liberating  more and more atomic oxygen  facilitating the  recombination  process (fast  phase  change  annealing). The slopes of linear portions of these curves (Figure 8) give values of second order velocity constants, k_II at each annealing temperature. Except  for  an  initial  period  of the  recovery,  linearity  is  obtained  in  all  cases  suggesting  a  bimolecular  reaction. The first  order  contribution  for  different  species  are  obtained  by  extrapolating  the  second  order  plots  at various  temperatures  to  zero  time  and  the  difference  between  read  off  and  experimental  values  at a  particular  time  are  taken.  Plots of logarithm of these values against heating time are linear (Figure 9) whose slope will give first order velocity constants, k_I at each annealing temperature.  The values of k_I and k_II are given in Table 1. The Arrhenius plots of log k_I and log k_II against 1/T (Figure 10) yield the activation energy 29.33 and 79.77 kJ mol^-1 for the first and second order process respectively. Thus, as is evident from the Fletcher-Brown treatment of the data, annealing can be represented by a combination of a unimolecular and a bimolecular process. The mean values of the proportions of the original nitrite, which recombine by the first and second order mechanisms, are 56% and 44%, respectively.

Chemistry of annealing

The existence of a number of species in irradiated nitrate has been reported^{36, 14, 17}. With moderate doses of irradiation at room temperature, the damage fragments are mainly NO₂^–, O and O₂ with low concentration of NO, NO₂, O₂^–, O₃^– etc. The charged fragment is situated in the lattice position of the original ion and the neutral fragments some distance away from the damage site. In the annealing process, the neutral fragments undergo diffusive movement and reacts with the charged fragments to reform the target ion¹⁹.

The fast phase change recovery may be due to the rapid reaction of NO₂^– and O pairs as follows:

NO₂^– + O → NO₃^–.                                                                                                                 (6)

The first order disappearance of the nitrite is the recovery of closely correlated NO₂^– and O pairs:

NO₂^– + O → NO₃^–                                                                                                                                  (7)

The second order reaction is the random recombination of NO₂^– and O or O₂ fragments which have diffused farther apart. The second order reaction of nitrite and atomic oxygen is only possible when the species are present in equal concentration but there will be competition between the following reactions:

O + O → O₂                                                                                                                                                 (8)

and

NO₃^– + O → NO₂^– + O₂                                                                                                                          (9)

with reaction (7). The trapped oxygen released upon dissolution is shown to be primarily molecular in nature⁸. The more plausible second order process is:

2NO₂^– + O₂ → 2NO₃^–.                                                                                                                           (10)

 

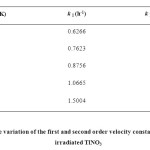Table 1:  Temperature variation of the first and second order velocity constants in the annealing of γ-irradiated TlNO3   Click here to View table

Fig. 1: FT-IR spectra of  TlNO3: a, unirradiated and b, γ-irradiated  Click here to View figure

Fig. 2: TG and DTA curves of untreated TlNO3 Click here to View figure

Fig. 3: Plot of fraction annealed (j) against heating time (t) for the isothermal annealing of γ–  irradiation damage in TlNO3 Click here to View figure

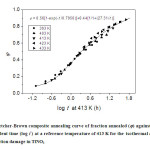Fig. 4: The Fletcher-Brown composite annealing curve of fraction annealed (j) against  logarithm of equivalent time (log t’) at a reference temperature of 413 K for the  isothermal annealing of γ-irradiation damage in TlNO3  Click here to View figure

Fig. 5: Energetics of Fletcher-Brown (FB) and Waite (W) model for γ-irradiated TlNO3 in the temperature range 393-433 K Click here to View figure

Fig. 6: Annealing as a function of the square root of heating time (t1/2) for γ-irradiated TlNO3 Click here to View figure

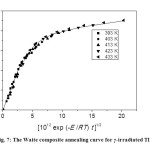Fig. 7: The Waite composite annealing curve for γ-irradiated TlNO3  Click here to View figure

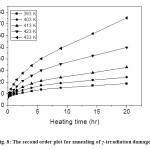Fig. 8: The second order plot for annealing of γ-irradiation damage in TlNO3 Click here to View figure

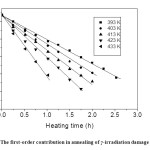Fig. 9: The first-order contribution in annealing of γ-irradiation damage in TlNO3  Click here to View figure

Fig. 10: Energetics of conventional chemical kinetics for γ-irradiated TlNO3 in  the temperature range 393-433 K Click here to View figure

 

CONCLUSIONS

The FT-IR and spectrophotometric estimations provide additional evidence for the formation of NO2- ions upon γ-irradiation of TlNO3. DTA has been used to confirm previously reported temperatures for two solid-solid transformations and for the melting of TlNO3. The present investigations revealed that the recovery of damage in irradiated sample occurs due to thermal reactions as well as reactions accompanying phase transformations in the damaged crystals. The isothermal annealing process is found to consist of a fast first-order reaction, in addition to a slow predominant second-order reaction. It has been suggested that the unimolecular process corresponds to the recombination of closely correlated NO and O2- pairs and the second order process to the random recombination of the damage fragments throughout the crystal.

ACKNOWLEDGEMENTS

The authors gratefully thank the Rubber Board, Kottayam, Kerala for lending irradiation facility.

REFERENCES

1. N. F. Mott and H. S. W. Massey, The Theory of Atomic Collisions, Clarendon Press, Oxford, (1949).
2. H. S. W. Massey and E. H. S. Burhop, Electronic and Ionic Impact Phenomena, Clarendon Press, Oxford, (1952).
3. F. Seitz and J. S. Koehler, Displacement of Atoms During Irradiations: Solid State Physics (Ed. F. Seitz, D. Turnbull) vol. 2, Academic Press, New York, (1956).
4. E. P. Wigner, J. Appl. Phys., 17: 857 (1946).
5. M. Burton, J. Phys. Colloid. Chem., 51: 611 (1947).
6. F. Seitz, Discuss. Faraday. Soc., 5: 271 (1949).
7. Y. A. Zakharov and V. A. Nevostruev, Russ. Chem. Rev., 37: 61 (1968).
8. E. R. Johnson, The Radiation Induced Decomposition of Inorganic Molecular Ions, Gordon and Breach Science Publishers, New York, (1970).
9. R. M. Golding and M. Henchman, J. Chem. Phys., 40:1554 (1964).
10. A. G. Maddock and S. R. Mohanty, Nature, 182: 1797 (1958).
11. A. G. Maddock and S. R. Mohanty, Discuss. Faraday. Soc., 31: 193 (1961).
12. S. Kaucic and A.G. Maddock, Trans. Faraday. Soc., 65: 1083 (1969).
13. S. R. Mohanty and P. Patra, Radiochim. Acta, 23: 152 (1976).
14. D. Muhammad and A. G Maddock, J. Chem. Soc. Faraday. Trans., 174: 919 (1978).
15. D. Bhatta, S. R. Mohanty and K.C. Samantaray, Radiochim. Acta, 28: 13 (1981).
16. D. Bhatta, P. Patra, and S. R. Mohanty, Indian. J. Chem. A, 21: 805 (1982).
17. D. Bhatta, P. Patra, and S. R. Mohanty, Radiochim. Acta, 35: 205 (1984).
18. S. M. K. Nair and C. James, Radiat. Eff., 62: 211 (1982).
19. B. M. Mohapatra and D. Bhatta, Radiat. Phys. Chem., 27: 339 (1986).
20. Proskurnin, Orekhov, Barelko Conf. Acad. Sci. U.S.S.R. on Peaceful Uses of Atomic Energy (Chem. Sci. Div.) p 41(1955).
21. R. P. Clark and F. W. Reinhardt, J. Therm. Anal., 13: 321(1978).
22. R. C. Flethcher and W. L. Brown, Phys. Rev., 92: 585 (1953).
23. T. R. Waite, Phys. Rev., 107: 463 (1957).
24. S. R. Mohanty and S. R. Upadhyay, Z. Phys. Chem. Neue., 57: 234 (1968).
25. M. B. Shinn, Ind. Engng. Chem., 13: 33 (1941).
26. N. F Kershaw and N. S. Chamberlin, Ind. Engng. Chem.,14: 312 (1942).
27. C. N. R. Rao, Chemical Applications of Infrared Spectroscopy, Academic Press, New York, (1963
28. K. Nakamoto, Infrared and Raman Spectra of Inorganic and Coordination Compounds, third ed. Wiley,New York, (1978).
29. Om Prakash and G. Jacob., Orient. J. Chem., 29(3), 1079-1084 (2013)
30. Neeti Rathore and B. Krishan., Orient. J. Chem., 29(3), 1001-1008, (2013)
31. J. Emsley, Chem. Soc. Rev., 9: 91 (1980).
32. N. Agrawal and A. N. Garg, Radiat. Phys. Chem., 73: 147 (2005).
33. B. M. Mohapatra and D. Bhatta, Indian. J. Chem. A, 23: 512 (1984).
34. V. Chakravortty, J. K. Mishra and S. R. Mohanty, Indian. J. Chem., 20: 77 (1981).
35. W. L. Brown, R. C. Flethcher and K. A. wright, Phys. Rev., 92: 591 (1953).
36. J. Cunningham, J. Phys. Chem., 67: 1771 (1963).

---

This work is licensed under a Creative Commons Attribution 4.0 International License.