A Prediction of the Elastic Behavior of Sodalite Zeolite: Molecular Dynamics Simulation

Introduction

Zeolite are nanoporous crystalline aluminosilicates frequently used in important chemical industry applications, such as pollution control, radioactive waste disposal,  gas purification, and petroleum production [1]. Their properties are determined by their nanoporous structures, which, in turn, are determined by the details of crystal growth processes [2]. They crystallize in a variety of low-density framework nanostructures built from corner-connected (Al,SiO₄) tetrahedral which define a narrow size distribution of pores and channel with molecular dimensions [3]. Despite their industrial use and wide research interest, there is little reported experimental work on the elastic properties of this class of materials [4,5,6].

Sodalite is an important zeolite because it forms a building block of more complex materials such as LTA and FAU [1]. Therefore, by investigating the properties of a sodalite cage, one can gain insights into the behavior of these more complex and technologically important zeolites. Sodalite has been studied previously using periodic first-principles calculations. [7, 8, 9].

In recent years, a number of experimental and theoretical studies have been carried out to investigate the structural and thermal properties of zeolites. Several groups have begun to investigate the elastic properties of zeolite structures using various computational methods [2,10,11].

In this paper, a detailed study on elastic properties of sodalite at normal condition is presented. In order to verify the predicted elastic properties of zeolites, it is important to have access to experimental data concerning elasticity.

Methodology

Computational details

The interatomic potential model employed here is based on and three-body interactions as implemented in the GULP code [12]:

The  two-body  interactions  were  treated  by  means  of  the classical  Buckingham  potential  to  describe  Cation-O  and  O–O  inter-actions  and  a  Coulomb  term:

Where r_ij is  the  bond  length  between  ions  i  and  j;  qi is  the  charge of ion i. The Buckingham potential (short-range) is composed of an exponential and the C/r⁶ terms describing the repulsive and an attractive energy, respectively. The Electrostatic Coulomb

Interactions part of potential (long-range) was calculated by the Ewald summation [13] using formal charges on all atoms. The corresponding values of the parameters A, ρ and C are given in Table 1.

Table 1: Potential used in simulation.

	Two body short range interaction
Atom1	Atom2	Potential	A(eV)	ρ(Å)	C(eVÅ6)
Si1 (core)	O1 (shell)	Buckingham	0.128E+04	0.321	10.07
Al1 (core)	O1 (shell)	Buckingham	0.146E+04	0.299	0.00
O1 (shell)	O1 (shell)	Buckingham	0.228E+05	0.149	27.9
	Shell model interaction
O1  (core)	O1 (shell)	Spring (core-shell)	K2 (evÅ-2)74.9
General Three-body potentials (Harmonic form)
Atom 1	Atom 2	Atom 3	Kthb(eV rad−2)	θ (°)	rmax (Å)
Si1(core)	O1(shell)	O1 (shell)	2.097	109.470	1.90
Al1(core)	O1(shell)	O1 (shell)	2.097	109.470	1.90

The  oxygen  ions  are  modelled  using the  core-shell  model,  where  a  mass  shell  is  linked  to  the  core  ideal harmonic  interaction  as:

Where k₂ is the harmonic force constant and r is the distance of separation between the centres of core and shell. A harmonic potential was chosen to describe three-body bond-bending interactions as:

Where k_ijk are  constants  determining  the  strength  of  the  interaction, θ_ijk is  the  angle  between  i-j  and  j-k  bonds  and  θ₀ is  the  equilibrium bond  angle.

Table 2: The experimental and simulated unit cell, atomic coordinates of SOD zeolite.

Structure	Experimental [14]	Simulated (this study)
a (Å)	8.840	8.890
b(Å)	8.840	8.890
c(Å)	8.840	8.890
α=β=γ	90.00	90.00
Si1 x,y,z	0.2500,0.500,0.00	0.2500,0.500,0.00
O1 x,y,z	0.136, 0.4338, 0.1490	0.1397,0.1506,0.4399
Al1 x,y,z	0.2500,0.00,0.500	0.2500,0.00,0.500
O2 x,y,z	0.139, 0.1506, 0.4390	0.1397,0.1506,0.4399
Total lattice energy    (eV) (primitive unit cell)	–	-1298.5372
Volume (Å3)	690.81	702.60

Table 3: Angle and interatomic distance for simulated of SOD zeolite.

Atom1	Atom2	d1,2 [Å]	Atom3	d1,3 [Å]	Angle (2,1,3) [°]
O1Si1	Si1O1	1.61041.6104	Al1O1	1.74691.6104	138.810107.524
	O1	1.6104	O1	1.6104	113.440
	O1	1.6104	O1	1.6104	107.524
	O1	1.6104	O1	1.6104	107.524
	O1	1.6104	O1	1.6104	113.440
	O1	1.6104	O1	1.6104	107.524
Al1	O1	1.7469	O1	1.7469	111.212
	O1	1.7469	O1	1.7469	108.608
	O1	1.7469	O1	1.7469	108.608
	O1	1.7469	O1	1.7469	108.608
	O1	1.7469	O1	1.7469	111.212

Table 4: Calculated  Elastic constants.

	Ultra sound [16]	Corrected  Ultrasound data [10]	Modelling prediction [10]	This work
C11 (GPa)	88.52	100.05	144.9	75.646
C12 (GPa)	38.70	24.90	38.58	46.318
C44 (GPa)	36.46	27.19	39.27	23.6406

Table 5: Mechanical properties of sodalite: bulk, shear, Poisson’s ratios and Young moduli.

	Ultra sound [16]	Corrected  Ultrasound data [10]	Modelling prediction [10]	This work
Bulk  Modulus:Ks (GPa)	55.30	51.45	74.03	56.094
Shear  Modulus: G(GPa)	31.30	24.89	39.27	20.05
Young moduli: E(GPa)	64.98	88.45	128.7	40.669
Poisson’s ratios: υ	0.304	0.213	0.210	0.37

Table 6: Static and high frequency dielectric constant tensor.

Indices	Static Dielectric constant			High frequency dielectric constant tensor
	1	2	3	1	2	3
x	3.92962	-0.13137	0.17135	1.64828	0.00000	0.00000
y	-0.13137	4.16670	-0.70137	0.00000	1.64828	0.00000
z	0.17135	-0.70137	4.08174	0.00000	0.00000	1.64828

Table 7: Piezoelectric strain and stress matrix.

	Indices	1	2	3	4	5	6
Piezoelectric Strain Matrix: (Units=Cm-2)	X	-2.43181	-1.48792	-1.36823	1.06598	0.07381	0.52346
	Y	1.13377	-0.10444	-0.46928	2.54216	0.91220	-0.92350
	Z	-1.07410	0.06944	0.55346	-2.66779	-0.84659	1.02716
Piezoelectric Stress Matrix: (Units=10-11 C/N)	X	-3.32901	-0.11070	0.29740	4.50912	0.31221	2.21426
	Y	3.34013	-0.88169	-2.12564	10.75338	3.85860	-3.90644
	z	-3.23883	0.66019	2.31051	-1.28478	-3.58108	4.34491

Table 8: Static and high frequency refractive indices.

Indices	Static refractive			High frequency refractive
	1	2	3	1	2	3
N	1.84907	1.97080	2.20793	1.28385	1.28385	1.28385

Results and discussions

Simulation cell

All-silica sodalite has a highly symmetric body-centered-cubic structure with 36 atoms per unit cell. In this case, sodalite with structural formula O₂₄Si₆Al₆ belongs to cubic structure family with P-4 3 N space group (a =b=c=8.89 Å; α=β=γ=90°) (figure 1). This structure is characterized by a cubo-octahedral cavity formed by the corner sharing of alternating [SiO₄] and [AlO₄] tetrahedral. Table 2 shows the structure, cell parameter, and unique atomic coordinates of the experimental sodalite structure determined using XRD powder diffraction [14], in comparison with that of the simulated structure.

Figure 1 : Projection of sodalite  along c axe. Click here to View figure

Interatomic distances generated using the crystal data from experiment and modeling agree within ±0.02 Å, demonstrating that we are able to reproduce accurately the atomic-scale structure of SOD.

In table 3, interatomic distance and angles are represented. In fact, the center of terahedra is occupied by atom with relatively low electronegativities (Si^IV) or (Al^III) and in the center by oxygen anions (O^2-). The angle between O-Si-O is equal to 107.254° and close to the ideal value of 109° for a geometrically perfect tetrahedron. For the case of Silica tetrahedron, the Si-O-Si angle is usually in the domain of 140-165°; in our case Si-O-Al is characterized by a 138.810° value. For [SiO₄] tetrahedra the bond length is d(Si-O)≈1.59-1.64 Å  and for  [AlO₄] the bond length is usually d(Al-O)≈ 1.73 Å  .

Mechanical properties

The mathematical formulation of the mechanical properties is given in details in the paper of Gale and Rohl [15].

The elastic constant represent the second derivatives of the energy density with respect to strain:

(5)

where Cij is a component of the stiffness matrix, C, E is the energy expression, V is the volume of the unit cell, and εi and εj are strain components.

There by describing the mechanical hardness of the material with respect to deformation. Since there are 6 possible strains within the notation scheme employed here, the elastic constant tensor is a 6 x 6 symmetric matrix. The 21 potentially independent matrix elements are usually reduced considerably by symmetry.

For a cubic system, symmetry provides the following equivalent terms: C₁₁=C₂₂=C₃₃;C₄₄=C₅₅=C₆₆ and C₁₂=C₂₃=C₁₃.

The obtained elastic constants of Sodalite are compared in Table 4 with experimental measurements and previous theoretical studies. Values in this study are nearest to those found by Li [16] with an agreement of 7% and far to those presented by Williams [10], we note that sodalite present an isotropic elastic properties (C₁₁=C₂₂=C₃₃=75.646 GPa).

Like the elastic constant tensor, the bulk (Ks) and shear (Gs) moduli contain information regarding the hardness of a material with respect to various types of deformation.

The bulk modulus Ks is also related to the components of the elastic compliance (The elastic compliances, S, can be readily calculated from the above expression by inverting the matrix; S = C⁻¹). We can obtain a bulk modulus, for example, using the Reuss’s definition [13], the bulk modulus is described as follows:

Ks=(S₁₁+S₂₂+S₃₃+2(S₁₂+S₁₃+S₂₃))⁻¹      (6)

Experimentally, bulk modulus values for sodalite have been found between 51 and 55 GPa (Table 5). The theoretical models predicted a value of 74.03 GPa. In this study calculated value is equal to 56.094 GPa. The disagreement, between experiment and theory, can be explained by the fact that efforts to model the zeolite framework did not include cations within the framework structures.

Our predicted value of Shear modulus (Gs) is equal to 20.05 GPa, it is smaller than other condensed zeolite (Gs=31.6 GPa for NAT and 32.1 GPa for ANA, [3]), indicating that sodalite is more flexible. This is related to its relatively open framework structure (figure 1), which can be easily deformed by bending the Si-O-Al angle involving an oxygen atom shared by the [SiO₄] and [AlO₄] tetrahedral [15,16].

The young’s moduli, which represents the response to a uniaxial stress applied to the material, E_i for loading in the Ox_i  (i=1,2,3) directions are given by:

In this paper, young modulus is isotropic and equal to 40.66 GPa (Table 5). This calculated value is different from literature data [10, 16].

Another interesting mechanical property is Poisson’s ratio define like: ν_ij  in the  Ox_i-Ox_j planes (i,j=1,2,3) for loading in the Ox_i direction  (8)

Poisson’s ratio is in good agreement with experimental data (Table 5) and reflecting the isotropy of sodalite (For an isotropic material, the thermodynamically allowable range of Poisson’s ratio is -1 < (ν) < 0,5).

Acoustic velocities are key quantities in the interpretation of seismic data. The polycrystalline averages of these acoustic velocities in a solid can be derived from the bulk and shear moduli of the material, as well as the density, ρ. There are two values, that for a transverse wave, Vs and that for a longitudinal wave, Vp, which are given by the following equations:

In this study Vp=22.14 Km/s, Vs=10.89 Km/s and giving Vp/Vs ratio equal to 2.03; this ratios is relatively high by comparing to those found for NAT (1.76) and ANA (1.77) [3].

The static (and high frequency) dielectric constant (3 × 3) tensor can be determined from the Cartesian second derivative matrix of all particles, D_αβ, and the vector, q, containing the charges of all particles [15]:

The computed static and high frequency dielectric constant tensor are given in Table 6.

The piezoelectric strain constants, d, are calculated from the Cartesian second derivative matrices according to:

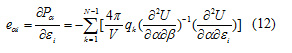
And the piezoelectric stress constants, e, are calculated according to:

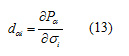
The above piezoelectric strain constants can be readily transformed into piezoelectric stress constants by multiplication by the elastic compliance tensor [15]. The obtained piezoelectric strain and stress are given in Table 7.

The refractive indices of a sodalite, υ, are simply related to the dielectric constant by:

The corresponding static and high frequency refractive indices are given in Table 8. For all computed quantities, the agreement between our computed quantities and available experimental and/or theoretical values is satisfactory. These quantities are useful in seismic research for predicting the mechanical properties of minerals, which are difficult to obtain experimentally.

Conclusion

This paper reports the prediction of the elastic constants of sodalite zeolite. The complete C_ij elastic moduli were determined using computer simulations. The result shows that the material is isotropic.

The inconsistency between the theory and experiments can be explained by the fact that the simulations were conducted in idealized zeolite cage framework, without charge-balancing cations or water molecules in the channels. The presence of extraframework cations in the channels is indeed thought to dramatically change the elastic properties of the zeolite.

Because of its structural flexibility, the bulk modulus and shear modulus values in sodalite are considerably smaller than those in densely packed cubic silicate structures such as spinel and garnet.

References

1. AUERBACH, S. M.; CARRADO, K.A.; DUTTA, P.K., Handbook of Zeolite Science and Technology, P. K., Eds. Marcel Dekker, New York, 2003.
2.  ASTALA, R.; AUERBACH, S. M.; MONSON, P. A. , J. Phys. Chem. B., 108, 9208 (2004).
3.  SANCHEZ-VALLE, C.; SINOGEIKIN, S.V.; LETHBRIDGE, Z.A.D.; WALTON, R.I. SMITH, C.W.; EVANS, J. K.E.; BASS, D., J. Appl. Phys., 98 053508, (2005).
4.  RYZHOVA, T.V.; ALEKSANDROV, K.S.; KOROBKOVA, V.M., Izv. Earth. Phys., 2 63, (1966).
5.  FREIMANN, R.; KUPPERS, H., Phys. Status. Solidi. A., 123,K123(1991).
6.  LETHERBRIDGE, Z. A.D; WALTON, R.I.; BOSAK, A; KRISCH, M., Chem. Phys. Lett., 471, 286(2009).
7.  TETER, D. M.; GIBBS, G. V.; BOISON, M. B. JR., ALLAN, D. C.; TETER, M. P. Phys. Rev. B.,  52, 8064(1995).
8.  SHAH, R.; GALE, J.; PAYNE, M.C., J. Phys. Chem., 100, 11688(1996).
9.  FILIPPONE, F.; BUDA, F.; IARLORI, S.; MORETTI, G.; PORTA, P., J. Phys. Chem., 99,12883(1995).
10.  WILLIAMS, J.J.; EVANS, K.E.; WALTON, R. I., Appl. Phys. Lett., 88, 021914(2006).
11.  KARMOUS, M.S., World J. Nano. Sci. Eng., 1, 66(2011).
12.  GALE, J.D., J. Chem. Soc., Faraday Trans., 93, 629(1997).
13.  EWALD, P., Ann. Der. Phys., 369, 253(1921).
14.  FELSCHE, J.; LUGER, S.; BAERLOCHER, CH., Zeol., 6, 367(1986).
15.  GALE, J.D.; ROHL, A.L., Mol. Simul., 29, 291(2003).
16. Li, Z.; NEVITT, M. V.; GHOSE, S., Appl. Phys. Lett., 55, 1730(1989).

---

This work is licensed under a Creative Commons Attribution 4.0 International License.