A Mechanistic Investigation of Stable Phosphonate Ester Derived from 3, 4 dichloro Aniline: A Kinetics Study and Theoretical Calculations

Introduction:

 In organicsynthesis, phosphonates are used in the Horner-Wadsworth-Emmons reaction. Aminophosphonates can also be used as a sole nitrogen source by some bacteria. Phosphonates have a very strong interaction with surfaces, which results in a significant removal in technical and natural systems ^1-4. The polyphosphonates used in industry differ greatly from natural phosphonates such as 2-aminoethylphosphonic acid, because they are much larger, carry a high negative charge and are complexed with metals. Several compounds containing a phosphate group (e.g., inositol phosphates, nuclcotidcs) or a phosphonate group (e.g., phosphonoformatc (Foscarnct, PFA), bisphosphonatcs) are of therapeutic interest acting antiviral, anticancer and anti-HIV agents. ⁵ Phosphonate and Phosphate derivatives often possess interesting enzyme inhibitory activities in vitro, and consequently are considered as potential drug candidates. ⁶ There are several features which taken all together allow one to consider that phosphorus containing compounds, like phosphonates, are excellent candidates for low molecular weight inhibitors of peptide bond cleaving proteolytic enzymes ^7-9.Phosphonates can be synthesized using the Michaelis–Arbuzov reaction. In one study a α-aminophosphonate is prepared by condensation of benzaldehyde, aniline, and trimethyl phosphite catalyzed by Copper triflate in a one-pot synthesis.¹⁰ In recent excellent review published by Orsini et al. ¹¹ phosphonate and phosphinate analogues ¹² of natural and non-natural aminoacids are among the most active organophosphorus inhibitors of aminopeptidases, type of proteases which selectively hydrolyze an amino acid residue from the Nterminus of proteins and peptides. They efficiently block bimetallic Zn-related aminopeptidases, i.e. leucine, alanine and methionine aminopeptidase ^13–15. The same electrostatic interaction between a negatively charged phosphonate group and the amino acid residue NH3⁺, together with some hydrophobic interactions, was used in host–guest type recognition of amino acids by various calixarene derivatives ^{16, 17}. In recent years, an enormous research potential was addressed towards the development of novel drug delivery systems, aiming to direct the drugs where they are specifically needed and to release them in a controlled manner. Among all the new drug delivery technologies, silica-based ordered mesoporous materials are particularly attractive ^{18, 19}, and have found applications in bone tissue regeneration ²⁰. Also binary, Zr-containing mesoporous silicas were proposed as drug delivery systems ²¹. Phosphonate ester and their derivatives are valuable chemical tools in probing cellular functions. ²² Many organic phosphonate ester have biological and pharmacological ^23-25 attributes and some of them are used as pesticides. Some bacteria use phosphonates as a phosphorus source for growth. The phosphonates (and other phosphorus esters) can also be synthesized via transesterification reaction catalyzed by organic catalysts. N-heterocyclic carbenes have been reported to catalyze the reaction efficiently.²⁶

And also, chlorinated anilines such as 3,4-dichloroaniline (DCA) are intermediates in chemical synthesis as well as being metabolites of acylanilide, phenylurea, and carbamate pesticides ^{27, 28}. DCA can persist in the environment as insoluble residues in soil and plants and can also photodimerise to form carcinogens ²⁹. Consequently, DCA has been classified as a compound of environmental concern, with substantial interest in its metabolic fate in plants ^{30, 31}. 3,4-dichloroaniline is one of the substrates in enzyme which belongs to the family of transferases, specifically those acyltransferases transferring groups other than aminoacyl groups. ³²

Herein, for the first time, we describe kinetics and a full mechanistic investigation of the reactions between triphenyl phosphite 1, dialkyl acetylenedicarboxylates 2, in the presence of a NH-acid such as 3,4-dichloroaniline 3 for the generation of stable phosphonate esters 4. In fact, in recent works triphenyl phosphite has been used instead of triphenylphosphine in the previous work.^33-41 In addition, the product is phosphonate esters 4 not phosphorus ylides. Synthesis of compounds 4, shown in Figure 1, has been reported earlier. ⁴²

  Material and methods

 Dialkyl acetylenedicarboxylates, triphenyl phosphite and 3, 4-dicholoro aniline were purchased from Fluka (Buchs, Switzerland) and used without further purification. All extra pure solvents including the n-hexane and 1, 2-dichloroethane was also obtained from Merck (Darmstadt, Germany). A Cary UV/Vis spectrophotometer model Bio-300 with a 10 mm light-path quartz spectrophotometer cell was employed throughout the current work. All structures, were optimized at the HF/6-31G (d, p) ^{43, 44} level of theory using the Gaussian 03 ⁴⁵ and AIM 2000 program package ⁴⁶.

 Experimental

 To gain further insight into the reaction mechanism between triphenyl phosphite 1, dialkyl acetylenedicarboxylates 2 and 3, 4-dicholoro aniline 3 (as a protic/nucleophilic reagent) for the generation of phosphonate ester 4 (Figure 1), a kinetic study of the reactions was undertaken using UV spectrophotometery technique. The relevant spectra from reaction between 1, 2 and 3 (10^-3M concentration of each compound) in 1, 2-dicloroethane at 25^˚C was recorded over the wavelength range 190-400 nm. The ultra-violet spectra shown in Figure 2 are typical.

From this, the appropriate wavelength was found to be 330 nm (corresponding mainly to product 4). Since at this wavelength, compounds 1, 2, and 3 have relatively no absorbance value, it provided the opportunity for full investigation of the kinetics of the reaction between triphenyl phosphate 1, dimethyl acetylenedicarboxylate 2 and 3, 4-dicholoro aniline 3.

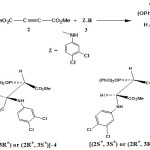Figure1: i) The reaction between triphenyl phosphate 1, dimethyl acetylenedicarboxylate 2 and 3, 4-dicholoro aniline 3 for the generation of stable phosphonate ester 4. j) Two isomers of compound 4 with Anti and Gauche arrangements Click here to View figure

Figure 2: i) The UV spectra of the reaction between 1, 2 and 3 with 10-3M concentration of each compound as the reaction proceeds in 1, 2-dichloroethane with a 10 mm light-path cell. j) Expanded section of UV spectra over the wavelength range 310-360 nm.  Click here to View figure

 

The reaction kinetics was followed by plotting the UV absorbance against time at wavelength 330 nm. Figure 3 shows the absorbance change (dotted line) versus time for the 1:1:1 addition reaction between compounds 1, 2 and 3 at 25.0 ºC. The infinity absorbance (A_∞) that is the absorbance at reaction completion, can be obtained from Figure 3 at t =620 min. With respect to this value, zero, first or second curve fitting could be drawn automatically for the reaction by the software associated ⁴⁷ with the UV instrument. Using the original experimental absorbance versus time data provided a second-order fit curve (solid line) that fits exactly with the experimental curve (dotted line) as shown in Figure 4. Thus, the reaction between triphenyl phosphite 1, dimethyl acetylenedicarboxylate 2 and 3, 4-dicholoroaniline 3 follows second-order kinetics. The second-order rate constant (k₂) is then automatically calculated using a standard equation ³⁵ within the program at 25.0ºC. They are reported in Table 1. Furthermore, kinetic studies were carried out using the same concentration of each reactant in the continuation of experiments with concentrations of 5×10^{-3 M and 7×10-3} M, respectively. As expected, the second-order rate constant was independent of concentration and its value was the same as in the previous experiment. In addition, the overall order of reaction was also 2.

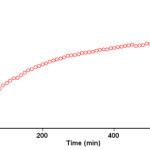Figure 3: The experimental absorbance changes (dotted line) against time at 330 nm for the reaction between compounds 1, 2 and 3 at 25.0 ºC in 1, 2-dichloroethane. Click here to View figure

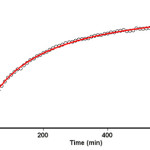Figure 4: Second order fit curve (solid line) accompanied by the original experimental curve (dotted line) for the reaction between compounds 1, 2 and 3 at 330 nm and 25.0 ºC in 1,2-dichloroethane.  Click here to View figure

 

Table 1: Values of overall second order rate constant for the reaction (1, 2 and 3)  in the presence of solvents such as 1,2-dichloroethane and a mixture of n-hexane /1, 2-dichloroethane (50:50) respectively, at all temperatures investigated.

Reaction		Solvent	ε	k2.M-1.min-1
				20.0ºC	25.0ºC	30.0ºC	35.0ºC
1, 2 and 3		1,2-dichloroethane	10	4.48	6.68	12.39	22.19
		Mix 50:50 1,2-dichloroethane and n-hexane	<10	2.22	5.04	9.48	16.77

 

Results and Discussion

Effect of Solvent and Temperature

To determine the effects of temperature and solvent environment change on the rate of reaction, it was elected to perform various experiments at different temperatures and solvent polarities but otherwise under the same conditions as the previous experiment. For this purpose, 1, 2-dichloroethane with 2 dielectric constant was chosen as a suitable solvent since it could not only dissolve all compounds but also did not react with them. The results (see Table 1) show that the rate of reaction in each case was increased at higher temperatures. In addition, the rate of reaction between 1, 2 and 3 declined in a lower dielectric constant environment (mixture of n-hexane /1,2-dichloroethane 50:50) in comparison with a higher dielectric constant environment (1,2-dichloroethane) at all investigated temperatures (reaction 1, 2, 3). In the temperature range studied, the dependence of the second-order rate constant (lnk₂) of the reactions on reciprocal temperature is consistent with the Arrhenius equation, giving activation energy (78.4 kj.mol ^-1 ) of the reaction from the slope of Figure 5.

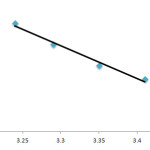Figure 5. Dependence of second order rate constant (lnk2) on the reciprocal temperature for the reaction between compounds 1, 2 and 3 measured at wavelength 330 nm in 1,2-dichloroethane. Click here to View figure

Effect of Concentration

To determine the reaction order with respect to triphenyl phosphite 1 (TOPP) and dimethyl acetylenedicarboxylate 2 (DMAD), in the continuation of experiments, all kinetic studies were carried out in the presence of excess 3 (Z-H). Under this condition, the rate equation may therefore be expressed as:

 

In this case (3×10^-2 M of 3 [Z-H] instead of 3×10^-3 M) using the original experimental absorbance versus time data provides a second order fit curve (solid line) against time at 330 nm which fits the experimental curve exactly. The value of rate constant was the same as that obtained from the previous experiment (3×10^-3 M). Repetition of the experiments with 5×10^-2M and 7×10^-2M of 3 (Z-H) gave, separately, the same fit curve and rate constant. In fact, the experimental data indicated that the observed pseudo second order rate constant (k_obs) was equal to the second order rate constant (k₂), this is possible when γ is zero in equation (1). It is appears, therefore, it appears that the reaction is zero and second order with respect to 3 (NH-acid) and the sum of 1 and 2 (α + β = 2), respectively.

To determine the reaction order with respect to dimethyl acetylenedicarboxylate 2 (DMAD), the continuation of the experiment was performed in the presence of excess of 1 (rate ₌ k΄_obs[Z-H]^γ [DMAD]^β, k΄_{obs =} k₂ [TOPP]^α (2)). The original experimental absorbance versus time data provides a pseudo-first-order fit curve at 330 nm, which exactly fits the experimental curve (dotted line) as shown in Figure 6.

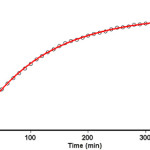Figure 6. Pseudo first order fit curve (solid line) for the reaction between 2 and 3 in the presence of excess 1 (10-2 M) at 330 nm and 25.0 ˚C in 1, 2-dichloroethane Click here to View figure

 

As a result,  since γ = 0 (as determined previously), it is reasonable to accept that the reaction is first order, (see first order fit in Figure 6) with respect to compound 2 (DMAD) (β =1). Because the overall order of reaction is 2 (α + β + γ =2) it is obvious that α ₌ 1 and order of triphenyl phosphite 1 (TOPP) must be equal to one.

 

Based on the above results, a simplified speculative proposed reaction mechanism is presented in Figure 8 in accord with the full reaction mechanism in Figure 7.

Figure 7. Speculative proposed mechanism for the reaction between 1, 2 and 3 for the generation of phosphonate ester 4. Click here to View figure

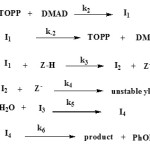Figure 8. Simplified scheme for Proposed mechanism of the reaction between 1, 2 and 3 for the generation of phosphonate ester 4 Click here to View figure

 

In order to determin the rate determining step of the proposed mechanism first, the rate law is written using final step for formation product.

Rate=k₆ [I₄]                                                                                                                  (3)

We can apply the steady-state approximation for intermediates such as [I₄], [I₃], [I₂] and [I₁] .To obtain a suitable expression for [I₄], [I₃], [I₂] and [I₁] we can assume that, after an initial brief period, the concentration of [I₄], [I₃], [I₂] and [I₁] achieves a steady state with their rates of formation and rates of disappearance being balanced. Therefore,are zero and we can obtain expressions for the intermediates as follows:

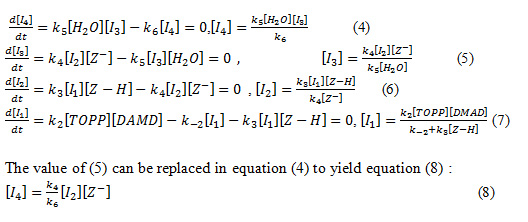
The value of (5) can be replaced in equation (4) to yield equation (8) :

And with the replacement of equation (6) in (8) the following equation is obtained:

By substituting (7) in (9) equation (10) is generated:

Now the value of (10) can be replaced in equation (3) to yield equation (11).

Since equation (11) is independent of k₆ (rate constant), thus the sixth step could not be the rate determining step. Also k₅ and k₄ do not appear in equation (11), so fourth and fifth steps could not be a rate-determining step (RDS).

Furthermore, we have investigated why steps such as 4 and 5 are capable of being determining steps. The reasons are discussed in detail bellow.

If we assume that the fifth step (rate constant k₅) is the rate-determining step for the proposed mechanism, in this case the rate law can be expressed as follows:

The steady state assumption can be applied for obtaining the concentration of intermediates and by substituting (7) in (6) equation (13) can be expressed:

The value of (13) can be replaced in equation (5) to yield equation (14):

And with the replacement of equation (14) in (12) the following equation is obtained:

And this equation is the same as equation (11) which we had already obtained with the assumption that the rate-determining step is relative to the sixth step. Furthermore, in the fifth step the solvent with the high dielectric constant (1, 2-dichloroethane) must be able to stabilize the dipolar intermediate I₃ which has full positive and negative charges and reduces the rate of reaction. Whereas, in practice, the rate of reaction increased with presence of solvents with high dielectric constant so, the effect of the solvent in reaction showed that step five (k₅) couldn’t be a rate-determining step.

If we assume that the fourth step (rate constant k₄) is the rate-determining step for the proposed mechanism, in this case, there are two ionic species to consider in the rate determining step, namely phosphonium ion (I₂) and 3,4 dichloro aniline ion (Z^–). The phosphonium and 3,4 dichloro aniline ions, as we see in Figure 7, have full positive and negative charges and form very powerful ion-dipole bonds to the 1, 2-dichloroethane, the high dielectric constant solvent. However, the transition state for the reaction between two ions carries a dispersed charge, which is divided between the attacking 3,4 dichloro aniline and the phosphonium ions. Bonding of solvent (1, 2-dichloroethane) to this dispersed charge would be much weaker than to the concentrated charges of 3,4 dichloro aniline and phosphonium ions. The solvent thus stabilize the species ions more than it does the transition state, and therefore E_a is higher, slowing down the reaction. However, in practice, 1,2-dichloroethane speeds up the reaction and for this reason, the fourth step, which is independent of the change in the solvent medium, can not be the rate determining step. Furthermore, the rate law for formation of the product (fourth step) in a proposed reaction mechanism with application of the steady state assumption can be expressed by: rate =k₄ [I₂] [Z^–]

By application of the steady state for [I₂] and [Z^–], and replacement of their values in the above equation, the following equation is obtained:

This equation is independent of the rate constant for the fourth step (k₄) and shows why the fourth step would not be affected by a change in the solvent medium. In addition, it has been suggested earlier that the kinetics of ionic species^‘ phenomena (e.g. the fourth step) are very fast ^48-50. This step cannot be the rate-determining step like steps 5 and 6.

As we saw in above, the fourth, fifth and sixth steps can not be RDS so in bellow, the three remaining steps (1, 2 and 3) are investigated for being the rate-determining step.

If we assume that the third step (rate constant k₃) is the rate-determining step for the proposed mechanism, in this case the rate law can be expressed as follows:

The value of (7) can be replaced in equation (17) to obtain this equation:

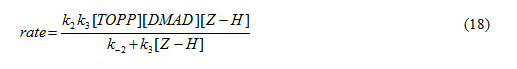
Since it was assumed that k₃ is relevant to the rate determining step, it is reasonable to make the following assumption: k_-2>>k₃ [3]

 

The final equation indicates that the overall order of reaction is three which is not compatible with the experimental overall order of reaction (=two). In addition, according to this equation, the order of reaction with respect to 3,4 dichloro aniline 3 is one, whereas it was actually shown to be equal to zero. For this reason, it appeared that the third step is fast.

If we consider the second step as a RDS, the rate law of reaction can be expressed as follows:

 

With the replacement of equation (6) in (19) the following equation is obtained:

 

Since it was assumed that k_-2 is relevant to the rate determining step, it is reasonable to make the following assumption:

k₃[Z-H]>>k_-2

 

So the rate of low becomes:

 

The final equation (21) shows that overall rate of reaction is reduced with the concentration of Z-H which is not compatible with the experimental overall rate of reaction. In fact, it was practically independent of the concentration of Z-H (3) and was actually shown to be equal to zero. For this reason, it appeared that the second step (k_-2) is fast, and cannot be a RDS.

And also if we assume that the first step (rate constant k₃) is the rate-determining step for the proposed mechanism, in this case the rate law can be expressed as follows:

 

The rate law  of the reaction depends on two reactants (triphenyl phosphite 1 and dialkyl acetylenedicarboxylate 2), which as we see in Figure 7, have no charge and could not form strong ion-dipole bonds to the high dielectric constant solvent, 1,2-dichloroethane. However, the transition state carries a dispersed charge which here is divided between the attacking 1 and 2, hence; bonding of solvent to this dispersed charge is much stronger than the reactants, which lack charge. The solvent thus stabilizes the transition state more than it does the reactants and, therefore, E_a is reduced which speeds up the reaction. Our experimental results show that the solvent with a higher dielectric constant exerts a powerful effect on the rate of reaction (in fact, the first step has rate constant k₂ in the proposed mechanism) but the opposite occurs with the solvent of lower dielectric constant (see Table 1). Also this equation indicates that the overall order of reaction is two and it depends on the concentration of compounds 1 and 2 and is independent of the concentration of compound 3. In addition, according to this equation, the order of reaction with respect to TOPP, DMAD and N-H is 1, 1 and zero, respectively.

The results of the current work (effects of solvent and concentration of compounds) have provided useful evidences for steps 1 (k₂), 2 (k_-2), 3 (k₃), 4 (k₄), 5 (k₅) and 6 (k₆) of the reactions between triphenyl phosphite 1, dialkyl acetylenedicarboxylate 2 and 2-fluro aniline 3. fifth steps involving 2, 3, 4, 5 and 6 are not the rate determining step, although the discussed effects, taken altogether, are compatible with the first step (k₂) of the proposed mechanism and would allow it to be the rate-determining step. However, a good kinetic description of the experimental result using a mechanistic scheme based upon the steady state approximation for the generation of equation is frequently taken as evidence of its validity. With respect to equation 15 and the experimental results the first step (k₂) is a RDS and the third step (k₃) is a fast step so the following assumption is possible for k in relation to equation 15:

k_-2<<k₃[Z-H] then equation 15 is converted to the below equation

rete= k₂[TOPP][DMAD].

This equation which was obtained from a mechanistic scheme (shown in Figure 8)is compatible with the results obtained by UV spectrophotometery (equation 22). With respect to equation (22) that is the overall reaction rate, the activation parameters involving DG^#, DS^# and DH^# can now be calculated for the first step (rate determining step, k₂), as an elementary reaction, on the basis of the Eyring equation. The results are reported in Table 2.

Table 2: The activation parameters involving DG^#, DS^# and DH^#for the reactions between (1, 2and 3) in 1,2-dichloroethane 

Reaction	DG#(kJ.mol-1)	DH#(kJ.mol-1)	DS#(kJ.mol-1.K-1)
1,2and 3a	72.59	79.92	0.024

 

Further kinetic investigations

To confirm the above observations, further experiments were performed with di-tert-buthyl acetylenedicarboxylate (DTAD) 2b, under the same conditions used in the previous experiments. The values of the second-order rate constant (k₂) for the reaction between 1, 2b (DTAD) and 3 was practically unobtainable. It seems that both inductive and steric factors for the bulky alkyl groups in 2b (DTAD) extremely tend to reduce the overall reaction rate (see equation 22). In the case of dimetyl acetylenedicarboxylate 2 (DMAD), the lower steric and inductive effects of the dimethyl groups exert a powerful effect on the rate of reaction. In addition, the rate of reaction in the presence of triphenyl phosphite in the recent reaction was also reduced in relation to triphenylephosphine in the previous reaction ²⁶. The results are accumulated in Table 3, it seems that more stronger nucleophile such as triphenylphosphine cause a high acceleration in the rate of reaction in comparison with the weaker nucleophile (triphenyl phosphite).

Table 3: Values of overall second order rate constant for two reactions (1 (TPP), 2 (DMAD) and 3 (Z-H)) and (1 (TPP), 2 (DMAD) and 3 (Z-H)) in the presence of solvent in 1, 2-dichloroethane, respectively, at the two investigated temperatures ³⁶.

			k2.M-1.min-1
Reaction	Solvent	ε	20.0ºC	25.0ºC
(previous reaction) (TPP) 1, 2 and 3	1,2-dichloroethane	10	673.3	766.5
(recent reaction) (TOPP) 1, 2 and 3	1,2-dichloroethane	5	3.32	4.95

 

Theoretical calculation

High stereo selective synthesis of phosphonate ester has previously shown that compound 4 has a gauche arrangement with [(2S^*, 3S^*) or (2R^*, 3R^*)] configuration [42]. For assigning one of two possible isomer configurations [(2S^*, 3S^*) or (2R^*, 3R^*)] and [(2S^*, 3R^*) or (2R^*, 3S^*)] in phosphonate esters 4, their structures were first optimized at the HF/6-31G (d,p) ^{43, 44} level of theory by the Gaussian 03 program ⁴⁵. The relative stabilization energies for both isomers have been calculated at the HF/6-31G (d,p) ^{43, 44} level and B3LYP ^{51, 52} method with 6-311G(d,p) basis set. The number of critical points and intramolecular hydrogen bonds has been recognized as well as the charge of atoms that were constructed on the two isomers. In addition, J_x-y , the values of proton and carbon coupling constants, and also chemical shifts (δ^H_iso,δ^C_iso) have been calculated at the mentioned level using the SPINSPIN keyword. The results, altogether, reveal the effective factors on the stability of the two [(2S^*, 3S^*) or (2R^*, 3R^*)] and [(2S^*, 3R^*) or (2R^*, 3S^*)] isomers. The relative stabilization energies for the two isomers of phosphonate ester (see Figures 1) are reported in Table 4; as can be seen, for compound 4 (gauche arrangement), the [(2S^*, 3S^*) or (2R^*, 3R^*)] configurations is more stable than the anti arrangement with the [(2S^*, 3R^*) or (2R^*, 3S^*)] configuration at both the HF/6-31G(d,p) level and the B3LYP method with 6-311++G(d,p) basis set.

Table 4: The relative energy (kcal/mol) between the two possible isomer configurations of phosphonate ester 4 [(2S^*, 3S^*) or (2R^*, 3R^*)] or [(2S^*, 3R^*) or (2R^*, 3S^*)] obtained at the HF/6-31G (d,p) level and B3LYP method with 6-311++G(d,p) basis set.

 

Further investigation was undertaken to determine more effective factors in the stability of the two [(2S^*, 3S^*) or (2R^*, 3R^*)] and [(2S^*, 3R^*) or (2R^*, 3S^*)] isomers on the basis of AIM calculation at the HF/6-31G(d,p) level of theory by the AIM2000 program package ⁴⁶. In recent years, AIM theory has often been applied in the analysis of H bonds. In this theory, the topological properties of the electron density distribution are derived from the gradient vector field of the electron density Ñr(r) and on the Laplacian of the electron density Ѳr(r).

Figure 9a: Intramolecular hydrogen bonds (dotted line) in the two [(2S*, 3S*) or (2R*, 3R*)]-4 and [(2S*, 3R*) or (2R*, 3S*)]-4 geometrical isomers of phosphonate esters. b)  Click here to View figure

 

Partiial molecular graphs, including intramolecular hydrogen bonds critical points (BCPS) for the two rotational isomers such as [(2S^*, 3S^*) or (2R^*,3R^*)] and [(2S^*, 3R^*) or (2R^*,3S^*)]. Small red shapes and lines correspond to BCPS and bond paths, respectively.

The Laplacian of the electron density, Ѳr(r), identifies regions of space wherein the electronic charge is locally depleted [Ѳr(r) > 0] ⁵³. Two interacting atoms in a molecule form a critical point in the electron density, where Ñr(r) =0, which is called the bond critical point (BCP).

The values of the charge density and its Laplacian at these critical points give useful information regarding the strength of the H bonds ⁴⁶. The range of r(r) and Ѳr(r) are 0.002-0.035 e/a³₀ and 0.024-0.139 e/a³_0, respectively, if H bonds exist ⁵⁴. Typically, AIM calculation indicates intramolecular hydrogen bond critical points (H-BCP) for the two [(2S^*, 3S^*) or (2R^*, 3R^*)] and [(2S^*, 3R^*) or (2R^*, 3S^*)] isomers of phosphonate ester 4. Intramolecular H-BCP along with partial molecular graphs for the two rotational isomers are shown in Figs. 9 (dotted lines).

The electron densities (r) ×10³, Laplacian of electron density Ѳr(r) ×10³, and energetic density –H(r) ×10⁴ are also reported in Table 5.

Table 5: The values of ρ, Ѳρ and Hamiltonian -H(r) for both the configuration of 4 calculated at the BCP

[(2S*,3S*) or (2R*,3R*)]	ρ×103	Ñ2ρ×103	-H(r)×104	[(2S*,3R*) or (2R*,3S*)]	ρ ×103	Ñ2ρ×103	-H(r)×104
1	9.86	40.84	15.66	1	14.54	56.60	8.12
2	9.39	36.67	4.92	2	10.54	48.44	27.03
3	8.40	34.26	13.97	3	4.37	19.40	9.64
4	12.95	53.68	14.12	4	8.94	36.34	14.10
5	3.14	14.29	8.46	5	8.69	34.35	12.69

 

A negative total energy density at the BCP reflects a dominance of potential energy density, which is the consequence of an accumulated stabilizing electronic charge ⁵⁵.The most important geometrical parameters involving some H bonds (bond length and their relevant bond angle) are reported in Table 6.

Table 6: Most important geometrical parameters corresponding to H bonds (Bond Lengths) for the two isomers of 4

	[(2S*, 3S*) or (2R*, 3R*)]	[(2S*, 3R*) or (2R*, 3S*)]
C38O39…H53		2.57a (120.66)b
C38O40…O13		2.98 (118.17)
C28H32…O37		2.65 (109.59)
C5O6…C38		2.72 (90.86)
C27H30…O7		2.98 (129.99)
C8O9…H21	2.29a (100.23)b
C2H4…H27	2.09 (122.62)
C24H27…O32	2.88 (122.19)
P19O31…H51	2.62 (95.98)
P19O31…H40	2.60 (94.19)

^a Bond lengths are in angstroms

^bBond angles are in degrees

 

The numbers of hydrogen bonds in both categories [(2S^*, 3R^*) or (2R^*, 3S^*)]-4 , [(2S^*, 3S^*) or (2R^*, 3R^*)]-4 are 5 and 5, and the values of r and Ѳr(r) ×10³ is in the ranges 0.004-0.014 and 0.019-0.056 e/a³₀ , 0.003-0.012 and 0.014-0.053 e/a³₀, respectively. In addition, the Hamiltonians [-H(r) ×10⁴] are in the ranges 8.12-27.03 and 4.92-15.66 au, respectively (see Table 5 ). These HBs show Ѳr(r) > 0 and H(r) < 0, which according to the classification of Rozas et al ⁵⁶. are medium-strength hydrogen bonds. Dipole moment in [(2S^*,3R^*) or (2R^*,3S^*)]-4 (8.38D) is more than in [(2S^*,3S^*) or (2R^*,3R^*)]-4 (2.14D) and appears to be an effective factor in the instability of [(2S^*,3R^*) or (2R^*,3S^*)]-4, the value of -H_tot in [(2S^*,3R^*) or (2R^*,3S^*)]- 4 (71.58au) is more than in [(2S^*,3S^*) or (2R^*,3R^*)]-4 (57.13au) and is taken as an important factor in the stability of [(2S^*,3R^*) or (2R^*,3S^*)]-4 (Table 7).

 

Table 7: Most important geometrical parameters involving the value of -H_tot (in au), dipole moment (in d), and the number of hydrogen bonds for the two isomers of 4.

conformer	Dipole moment		NO. of HBS	-H(r)×104
[(2S*,3S*) or (2R*,3R*)] 4a		2.14a, 2.14b	5	57.13
[(2S*,3R*) or (2R*,3S*)] 4a		8.38, 7.41	5	71.58

^acalculated at HF/6-31G (d, p)

 

^bcalculated at B3LYP/6-311++G (d, p)

 

It seems that the instability in the [(2S^*,3R^*) or (2R^*,3S^*)]-4 stems from the two opposite factors (dipole moment and total Hamiltonian) in which the influence of dipole moments is superior to that of the total Hamiltonian, resulting in a considerable relative instability in [(2S^*,3R^*) or (2R^*,3S^*)]-4 (10.35 kcal/mol in comparison with the [(2S^*,3S^*) or (2R^*,3R^*)]-4 isomers). This behavior is in a good agreement with the experimental results based upon the ¹H, ¹³ C, and ³¹ P NMR data.[42] The individual chemical shifts have been characterized by NMR calculations at the mentioned level. The total spin-spin coupling constant is the sum of four components: the paramagnetic spin-orbit (PSO), diamagnetic spin-orbit (DSO), Fermi-contact (FC), and spin-dipole (SD) terms. The value of chemical shifts (d) and coupling constants (J_x-y) are reported in Tables 8 and 9. As can be seen, there is a good agreement between both the experimental and theoretical chemical shifts (d) and coupling constants (J_x-y). In the present work, molecular structures of phosphonate ester 4 involving four large atoms such as Chloro, Phosphorus, Oxygen and Nitrogen atoms are huge, with a large number of other atoms (C, H); for this reason, a basis set higher than HF/6-31G(d,p) is impossible for obtaining more accurate calculations in a higher performance. This limitation causes a difference between both the experimental and theoretical coupling constants and chemical shifts data in some functional groups.

 

Table 8: Selected ¹H NMR chemical shifts (d in ppm) and coupling constants (J in HZ) for some functional groups in the [(2S^*, 3S^*) or (2R^*, 3R^*)]-4 isomer

Groups	dH(ppm)	JPH(HZ)	JHH(HZ)
6H, 2s, 2OCH3	3.73a, 3.91a (3.66b, 3.92 b)
1H, dd, PCHCH	4.18 (3.92)	25.1	3.9 (6.1)
1H, m, PCHCH	5.0 (4.14)
1H, dd, PCHCHNH	6.58 (4.38)	2.7 (0.34)	8.8 (13.17)
1H, d, CHarom	6.75 (7.11)		2.5 (2.7)
1H, d, CHarom	7.05 (7.75)		8.2
1H, m, 2Oph, CHarom	7.12-7.32 (7.17- 7.51)

^a: Experimental data in accord with the results reported in literature ⁴²

^b: Theoretical data

 

Table 9: Selected ¹³C NMR chemical shifts (d in ppm) and coupling constants (J in HZ) for some functional groups in the [(2S^*, 3S^*) or (2R^*, 3R^*)]-4 isomer

Groups	dc(ppm)	JPc(HZ)
d, PCHCH	47.69a (41.29)b
2s, 2OCH3	53.05, 53.32 (44.71,45.33)
d, PCCH	55.57 (49.11)	3.0 (5.1)
s,Carom, CHarom	113.61 (113.02)
s, CHAROM	115.55 (113.02)
d,2Cortho	120.68 (119.51)
d, 2Cortho	120.37 (117.14)	4.3 (4.2)
2s, 2Cpara	125.41, 125.73 (120.54, 120.53)
2s, 4Cmeta	129.64, 129.95 (126.26, 125.93)
s, CHarom	132.94 (130.44)
s,Carom	145.50 (146.95)
d, Cipso	149.86 (144.29)	8.3 (5.4)
d, Cipso	150.15 (144.02)
d, CO	167.89 (162. 77)	5.3 (5.4)
d, CO	171.41 (164.77)

^a: Experimental data in accord with the results reported in literature ⁴²

 

^b: Theoretical data

Conclusion

Kinetic investigation of recent reactions was undertaken using UV spectrophotometry. The results can be summarized as follow: (1) the appropriate wavelengths and concentrations were determined to follow the reaction kinetics. (2) The overall reaction order followed second-order kinetics and the reaction orders with respect to triphenyl phosphite1, dialkyl acetylenedicarboxylate 2 and 2-fluro aniline 3 were one, one and zero, respectively. (3) The values of the second-order rate constants of all reactions were calculated successfully at all solvents and tempratures investigated (4) the rates of all reactions were accelerated at higher temperatures. The activation energy for the reaction with dimethyl acetylenedicarboxylate 2 (78.4 kJ.mol ^-1) in 1, 2-dichloroethane. In fact, the rate of reaction in the presence of triphenyl phosphite is much slower in comparison with those ylides that generated from triphenylphosphine. (5) The rates of all reactions were increased in solvents with higher dielectric constant and this can be related to differences in stabilization by the solvent of the reactants and the activated complex in the transition state (6). Increased steric bulk in the alkyl groups of the dialkyl acetylenedicarboxylates, accompanied by the correspondingly greater inductive effect, reduced the overall reaction rate. (7) With respect to the experimental data, the first step of the proposed mechanism was recognized as a rate-determining step (k₂) and this was confirmed based upon the steady-state approximation. (8) Also, the third step was identified as a fast step (k₃). (9) The activation parameters involving DG^#, DS^# and DH^# were reported for the reaction. (10) Theoretical calculations showed that phosphonate ester 4 with a gauche arrangement and [(2S^*, 3S^*) or (2R^*, 3R^*)] configuration is more stable than anti arrangement and a [(2S^*, 3R^*) or (2R^*, 3S^*)] geometry. These results are compatible with the data obtained from the ¹H, ¹³C and ³¹P NMR spectroscopy and X-ray crystallography data of compound 4 ⁴² which has an emphatic stress on the [(2S^*,3S^*) or (2R^*,3R^*)] configuration as a lone isomer of 4.

 

Acknowledgments

Authors sincerely thank the University of Sistan and Baluchestan for providing financial support of this work.

References

1. Stone A. T, Knight M. A., Nowack B. Speciation and chemical reactions of phosphonate chelating agents in aqueous media. In: Lipnick RL, Mason RP, Phillips ML, Pittman CU, editors. Chemicals in the environment: fate, impacts andremed iation, ACS Symposium Series No. 806. Washington, DC: American Chemical Society,. p. 59–94. (2001)
2. Xyla AG, Mikroyannidis J, Koutsoukos PG. The inhibition of calcium carbonate precipitation in aqueous media by organophosphorous compounds. J Colloid Interface Sci; 153:537, (1992).
3. Fischer K. Sorption of chelating agents (HEDP and NTA) onto mineral phases andsed iments in aquatic model systems, Part I: sorption onto clay minerals.
4. Chemosphere; 22:15, (1991).
5. Morillo E., Undabeytia T., Maqueda C. Adsorption of glyphosate on the clay mineral montmorillonite: effect of Cu(II) in solution andad sorbed on the mineral. Environ Sci Technol;31:3588, (1997).
6. Klerk J. M. H., van Dijk A, van het Schip AD, Zonnenberg BA, van Rijk PP. Pharmacokinetics of rhenium-186 after administration of rhenium-186-HEDP to patients with bone metastases. J Nucl Med;33: 646, (1992).
7. For a review on phosphonate analogs of nucleotides as antiviral agents, see: Holy, A. In Advances in Antiviral Drug Design; De Clercq, E., Ed.; JAI: Greenwich,; pp 179, (1993)
8. 7Weaver. L.H., Kester W.R.,. Matthews B.W., J. Mol. Biol. 114,119, (1977)
9. Jacobsen N.E., Bartlett P.A., J. Am. Chem. Soc. 103, 654, (1981)
10. Andersson L., Isley T.C., Wolfenden R., Biochemistry 21, 4177, (1982).
11. 10. Abhimanyu S. Paraskar and Arumugam Sudalai   Arkivoc (1838EP): 183, (2006).
12. Orsini F., Sello G., Sisti M., Curr. Med. Chem. 17, 264, (2010)
13. Mucha A., Lammerhofer M., Linder W., Pawełczak M., Kafarski P., Bioorg. Med. Chem. Lett. 18, 1550, (2008)
14. Drag M., Grembecka J., Pawelczak M., Kafarski P., Eur. J. Med. Chem. 40, 764, (2005).
15. Lejczak B., Kafarski P., Zygmunt J., Biochemistry 28, 3549, (1989).
16. Picha J., Liboska R., Budesinsky M., Jiracek J., Pawelczak M., Mucha A., J. Enz. Inhib. Med. Chem. 26, 155, (2011).
17. Mutihac L., Lee J.H., Kim J.S., Vicens J., Chem. Soc. Rev. 40 , 2777, (2011)
18. Kalchenko V.I., Pure Appl. Chem. 80, 1449, (2008).
19. Sanchez C., Belleville P., Popalld M., Nicole L., Chem. Soc. Rev. 40, 696, (2011).
20. Manzano M., Vallet-Regi M., J. Mat. Chem. 20, 5593, (2010).
21. Vallet-Regi M. , Colilla M., Izquierdo-Barba I., J. Biomed. Nanotechnol. 4, (2008)
22. Colilla M., Manzano M., Izquierdo-Barba I., Vallet-Regi M., Boissiere C., Sanchez C., Chem. Mater. 22, 1821, (2010).
23. Crews C. M.; Splittgerber, U. Trends Biochem. Sci., 24, 317, (1999).
24. Maghsoodlou M.T., Habibi-Khorassani S.M., Hazeri N., Nassiri M., Marandi G., Afshari G.and Niroumand U., Sulfur Chemistry, , 26, 261, (2005).
25. Islami M.R., Mollazehi F., Badiei A.and Sheibani H., Arkivoc, , 25, (2005).
26. Maghsoodlou M.T., Heydari R., Habibi-Khorassani S.M., Hazeri N., Lashkari M., Rostamizadeh M., Sajadikhah S.S., Synthetic Communications.,41, 569, (2011).
27. Singh R, Nolan S. P., Chemical Communications (43): 5456, (2005)
28. Parris, G.E.,. Residue Rev. 76, 1, (1980).
29. Van der Trenck K.T., Hunkler, D., Sandermann H.,. 36, 714, (1981).
30. Harvey P.J., Campanella B.F., Castro P.M.L., Harms H., Lichtfouse E., Scha ffner A.R., Smrcek S., Werck-Reichhart D.,. Environ. Sci. Pollut. Res. 9, 29, (2002).
31. Bartha R., You I. S., Saxena A, Pergamon, Oxford, 3, 345, (1983).
32. Sandermann H., Scheel D., v.d. Trenck T., Appl. Polym. Symp. 37, 407, (1983).
33. Matern U, Feser C, Heller W. Arch. Biochem. Biophys. 235 (1), 218, (1984)
34. Habibi-Khorassani S.M.,. Maghsoodlou M.T, Ebrahimi A., Saravani H., Zakarianejad M., Ghahramaninezhat M., Kazemian M.A., Nassiri M., Khajehali Z., Prog React Kinet Mech., , 34, 301, (2009).
35. Habibi Khorassani S.M., Maghsoodlou M.T., Ebrahimi A., Zakarianezhad M., Mohamadzadeh p., Shahraki M., Oriental Journal of chemistry., , 24, 73, (2008).
36. Zakarianezhad M., Habibi Khorassani S.M., Ebrahimi A., Maghsoodlou M.T., Ghasempour H., Heteroatom chemistry, , 21, 462, (2010).
37. Habibi Khorassani S.M., Maghsoodlou M.T., , Ebrahimi A., Zakarianezhad M., Dasmeh H. R., Cheistry: An Indian journal, , 3, (2006).
38. Habibi Khorassani S.M., Ebrahimi A., Maghsoodlou M.T., Kazemian M.A., Moradian M., Chinese Journal of Chemistry., , 28, 719, (2010).
    1. Kazemian M.A., Karimi P., Habibi-Khorassani S.M., Ebrahimi A., Maghsoodlou M.T., Jalili-Milani F., Prog React Kinet Mech., , 34, 77, (2009).
39. M. Shahraki, S. M. Habibi Khorassani, A. Ebrahimi, M. T. Maghsoodlou, Prog. React. Kinet. Mech., 37, 1, (2012).
    1. S. M. Habibi Khorassani, Maghsoodlou M.T., Aghdaei E.and Shahraki M, Prog. React. Kinet. Mech. 37, 1, (2012).
40. Habibi Khorassani S.M., Maghsoodlou M.T., Ebrahimi A., Roohi H., Zakarianezhad M.. Iran. Chem. Soc., , 3, 223(2006).
41. Maghsoodlou M.T., Hazeri N., Habibi-Khorassani S.M., Marandi G., Saghatforoush L., Saravani D., Akbarzadeh N., Rostami-Charati F., Khandan-Barani K., Skelton B. W., and Makha M., Heteroatom Chemistry., 21, 222, (2010).
42. Petersson G. A., Al-Laham M. A. J Chem Phys, 94,6081, (1991)
43. Petersson G. A., Bennett A., Tensfeldt T. G., Al-Laham M.A., Shirley WA, Mantzaris J J Chem Phys, 89, 2193.(1988), Becke A. D. Phys Rev A, 38, 3098, (1988)
44. 45.Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Montgomery, Jr., J. A.; Vreven, T.; Kudin, K. N.; Burant, J. C.; Millam, J. M.; Iyengar, S. S.; Tomasi, J.; Barone, V.; Mennucci, B.; Cossi, M.; Scalmani, G.; Rega, N.; Petersson, G. A.; Nakatsuji, H.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Klene, M.; Li, X.; Knox, J. E.; Hratchian, H. P.; Cross, J. B.; Bakken, V.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R. E.; Yazyev, O.; Austin, A. J.; Cammi, R.; Pomelli, C.; Ochterski, J. W.; Ayala, P. Y.; Morokuma, K.; Voth, G. A.; Salvador, P.; Dannenberg, J. J.; Zakrzewski, V. G.; Dapprich, S.; Daniels, A. D.; Strain, M. C.; Farkas, O.; Malick, D. K.; Rabuck, A. D.; Raghavachari, K.; Foresman, J. B.; Ortiz, J. V.; Cui, Q.; Baboul, A. G.; Clifford, S.; Cioslowski, J.; Stefanov, B. B.; Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Martin, R. L.; Fox, D. J.; Keith, T.; Al-Laham, M. A.; Peng, C. Y.; Nanayakkara, A.; Challacombe, M.; Gill, P. M. W.; Johnson, B.; Chen,W.; Wong, M. W.; Gonzalez, C.; and Pople, J. A.; Gaussian, Inc., Wallingford CT, (2004).
45. Biegler-konig F. W.; Schonbohm J.; Bayles D. J Comput Chem, 22, 545, (2001)
46. Schwartz L. M., Gelb, R. I.: Anal. Chem., 50, 1592, (1978).
47. 48.Treglon P. A., Laurence, G. S.: J. Sci. Instrum. 42, 869 (1956).
48. Wolff M. A., Chem. Instrum., 5, 59, (1976).
49. Okubo T., Maeda, Y.; Kitano, H. J. Phys. Chem., , 93, 3721, (1989).
50. Becke A. D. Phys Rev A, 1988, 38, 3098–3100
51. Lee C., Yang W., Parr R. G. Phys Rev B, , 37,785, (1988).
52. Bader R. F. W. Atoms in Molecules a Quantum theory; Oxford University: New York, (1990).
53. 55.  Grabowski S. J. J Mol Struct, 562, 137, (2001).
54. Arnold W. D.; Oldfield, E. J Am Chem Soc, 122, 12835, (2000).
55. Rozas I., Alkorta I., Elguero J., J Am Chem Soc, 122, 1115, (2000).

 

 

---

This work is licensed under a Creative Commons Attribution 4.0 International License.