Thermodynamic Deprotonation of  N, N' – Disubstituted Thiobarbituric Acids in Water – Dioxane Mixtures

Introduction

The studies on the behaviour of the heterocyclic imines and enols are of current interest in biopolymers and in the physical chemistry of drug action. It is desirable that more information is gathered about similar model systems. Thiobarbituric acids containing enolic and emine groups in a benzenoid heterocyclic ring system has been selected as one such model compounds Analytical applications of this family of compounds have been extensively examined in recant years. A knowledge of their deprotonation constants is needed for evaluating the complexing ability of these ligands with metal ions. Additionally the thermodynamic parameters so derived greatly help in correlating as well as studying the metal – Ligand reactions, with this view, the thermodynamic deprotonation pK_a^T“>   of N“> , N‘”>  diaryl thiobarbituric acids in different mole fraction of dioxane at 20, 30, and 40 ±0.01⁰C have been determined and the thermodynamic parameters associated with the deprotonation processes are evaluated.

Experimental

The N“> , N‘”>   diaryl substituted thiobarbituric acids were synthesised by the method described elsewhere⁷, recrystallized before use and purity was checked by elemental analysis UV and IR spectra. The other chemicals used were of Anala R and G.R grades of B.D.H or E. Merck unless otherwise stated. Dioxane was purified as recommended.⁷ An aqueous solution (10%) of tetra methyl ammonium hydroxide (TMAH) titrant was standardized against potassium hydroxide and diluted to 0.1 M, the proportions of dioxane and water being the same as used in preparing the titre solutions.

The titration procedure for determining the deprotonation constants was same as outlined by Albert and Sergeant⁸. Generally 0.01 M substituted thiobarbituric acids were titrated without the addition of inert salt. The measurements of pH were made on an expanded scale pH – meter [ELICO, Model No. pH 821 Hyderabad]. The instrument was standardized against Phthalate and borax buffers before and after each titration.

In a thermo stated (20, 30 and 40 ±0.01⁰C) titration vessel, accomodating a glass electrode, a limb of saturated KCl bridge and a micro burette of 5.0 ml capacity, 0.5 M of thiobarbituric acids in the appropriate dioxane water composition was taken and contents stirred magnetically. The initial volume of titre solution was 48 ml in all the cases to allow for the change in the total volume of solution on the addition of titrant. For practical purposes, the error caused by volume correction is almost negligible [Less than 0.01 pH unit for the inner five readings of a set of pH titrations] with a maximum error of 0.018 pH unit⁹. About 10 min. after the settings, the titration was started by adding 0.5 ml aliquots of 0.1 M TMAH at a time and noting the highest stable pH. The titrations, carried out in duplicate, were reproducible within ±0.01 pH unit.

The thermodynamic deprotonation constant pK_a^T“>  values have been determined by the pH – titration method employing a glass and saturated calomel electrode in cells with a liquid junctions potential. The relationship of Van Vitert and Hass¹⁰ was used to determine the H+”>  concentration from the values read on pH – meter [B].

-log [H⁺]=B+log U_H^O+log Y± _________________ 1

The values of the correction factor log U_H^O, were obtained experimetally¹¹ and those of the mean coefficient were (r±) computed by interpolation of the data given by Harned and Owen¹². Here the assumption has been made that the mean activity coefficients are same on both the molal and molar scales. The deprotonation of thiobarbituric acids [HA] in an aqueous medium gives [H⁺] and thiobarbiturate anion (A-). In such a medium, the equilibrium constant is given as follows

 

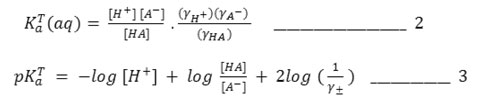
Assuming Y_HA, the mean activity coefficients of unionized acid, is unity, the final form of equations for computing pK_a^T in the dioxane – water mixture is obtained by equations 1 and 3.

 

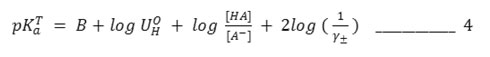
A correction for hydrolysis of the salt, which may be significant at the end of the titration (at pH >10) was applied by substituting log [HA]+[OH^–]/ [A^–] – [OH^–] for log [HA]/ [A^–] in equations 3 and 4. The hydroxyl ion activity [OH-] was computed from the relationship¹³.

[OH^–] = antilog [B-pK_w]

The ionic product of water, pK_w, has been obtained from the data of Agarwal¹⁴ in different dioxane – water mixtures.

The standard change in free energy [ΔG⁰], enthalpy [ΔH⁰] and entropy [ΔS⁰] associated with the deprotonation equilibrium, 15(i.e HA↔ H⁺+A^–) can be evaluated on the basis of equations (5) – (7).

 

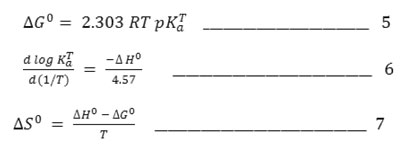
Result and Disscussion

The pK_a^T values of N, N’ disubstituted thiobarbituric acids in different dioxane – water mixtures at 20, 30 and 40⁰ C are given in table – 1. The pK_a^T values of these acids in all media invariably decrease with increasing temperature. The average pK_a^T usually falls within a spread of ± 0.02 but not beyond ± 0.03 in any instance. The empirical data for the mole fraction of dioxane (n₂) and ΔG⁰, ΔH⁰ and ΔS⁰  values are given in tables 2 and 3 respectively.

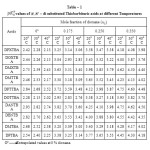Table1: pKaT values of N, N’ – di substituted Thiobarbituric acids at different Temperatures   Click here to View table

 

Effect of medium

The pK_a^T values of the acids are influenced by the intrinsic basicity of the solvent. The deprotonation equilibrium for substituted thiobarbituric acids is an inorganic reaction and therefore the changes in pK_a^T values with dioxane should be accounted for by the electrostatic and specific solvation effects, considering its acid dissociation involving a net increase of ions.

 

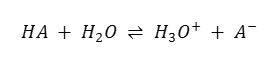
The decrease in the dielectric constant of the reaction medium enhances the electrostatic forces between the oppositely charged ions and thus facilitates the formation of molecular species which should increase the pK_a^T [table – 1]. This prediction has been simply confirmed for other reagents on the basis of previous studies.^{15 – 16} 

It has been proposed^{17 – 18} that the free energy of deprotonation of acids in solutions at its infinite dilution might be expressed as the sum of an electrostatic term [el] sensitize to the environment and a non-electrostatic term (nonel) insensitive to the environment and independent of temperature.

ΔG⁰_dess =ΔG⁰_el + ΔG⁰_nonel0 ______________________ 8

If the electrostatic part is expressed by Born’s formula¹⁹, the equation (8) takes the following form.

 

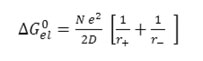
Where r+ and r- denote the radii of the solvated ions and D is the dielectric constants of medium. Hence

 

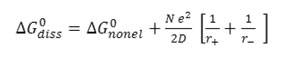
Further, as  ΔG⁰_diss=2.303 RT pK_a^T

The equation simplifies as

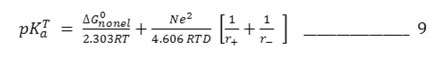
conventionally, pK_a^T is plotted against 1/D assuming ΔG⁰_nonel0 to be in dependent of solvent when values of substituted thiobarbituric acids are plotted against 1/D. It is observed that the plots have a distinct curvature. It seems evident that non-electrostatic factor exert a considerable influences on the deprotonation of substituted thiobarbituric acids.

Mole Fraction of dioxane

For substituted thiobarbituric acids, the change in pK_a^T with mole fraction of dioxane (n₂) is of considerable magnitude. Generally, the difference in pK_a^T in aqueous medium (n₂ = 0) and aqueous dioxane medium (n₂ = 0.350) is of the order of 1.8 – 2.50 pK_a^T units. When pK_a^T values of these thiobarbituric acids are plotted against n₂ , straight line relationship  are encountered (Fig. 1). The experimental values of pK_a^T indicate a maximum deviation form linearity of the order of 0.05 or about 0.5% inpK_a^T.

The goodness of fit in these instance was judged by calculating the correlation coefficient (m) defined by

 

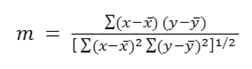
Where x^– and y^– are mean values of x(pK_a^T) and y (n2)”>  , respectively. The summations are extended to all pairs (x, y)”>  available. Linear proportionality is readily indicated between two variables¹⁹ when the values of m is +1.0.

Since the values of m is nearly +1.0 at 20, 30 and 40⁰C for all the substituted thiobarbituric acids [table – 2], it implies that there is quite a high probability of a linear relationship between pK_a^T and (n₂). A similar behaviour is found for several other acids²⁰ in aqueous-dioxane medium likewise linear proportionality is also obtained for some other mixed water solvents e.g. acetic acid, propionic acid, butyric acid and benzoic acid in methanol– water mixture.²¹

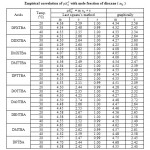Table2: Empirical correlation of pKaT with mole fraction of dioxane (n2)   Click here to View table

 

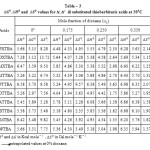Table 3  Click here to View table

 

Mean ionic radii (r±)

To provide an electrostatic interpretation of the medium effect on deprotonation process, Born’s solvation energy equation – 9 has been simplified by king²² as

 

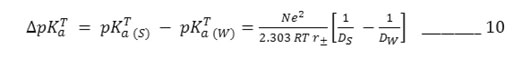
where r± , mean ionic radii, equal to

 

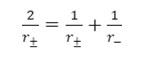
The values of r± have been computed via equation – 10 at different percentage and are in the range 2.15 – 2.75 A⁰. It is evident from this

computation process the value of r± increase slightly with aqueous dioxane concentrations. It is difficult to explain this variation with change in solvent composition. Similar increase in r± values has been encountered while studying the acids dissociation of other acids.^{23, 24}

Thermodynamic functions for ionic equilibria:-

The pK_a^T values have been determined with a precision of ±0.02 to ±0.03 and hence the error in ΔG⁰  is believed to be close to ± 0.03 and ± 0.04 Kcal. Mol^-1 . The values of ΔS⁰ given in Table -3 are accurate to ±0.20 cal. ^-1K^-1.

The positive values of ΔH⁰ found in aqueous as well as aqueous- dioxane mixture for all substituted thiobarbituric acids proves that acid dissociation at temperatures up to 40⁰C is endo – thermic. The positive value of ΔH⁰  encountered here may be ascribed to the breaking of the covalent bond between hydrogen and oxygen atoms of –OH group of thiobarbituric acids. Further it is evident that the magnitude of change in ΔH⁰  with solvent composition is relatively small and falls within the range of experimental error. It is because of this that slopes of straight lines in the plots of pK_a^T  against n₂ ( fig. 1) do not differ markedly and are nearly the same and parallel at these temperatures for all the thiobarbituric acids.

figure 1   Click here to View figure

 

The of ΔH⁰ are found to decrease with increase in dioxane content of the solvent medium for all thiobarbituric acids, thereby proving that is dependent of solvent composition. The negative value of entropy has been explained as arsing due to deprotonation of the legand since the sum of the total of the number of water molecules bound is more than water molecules originally accompanying the un dissociate thiobarbituric acids.

When acid dissociates in two media, the free energy change for transfer reaction from one medium to the other is given by 2.303 RT pK_a^T. For instance with DPTBA, ΔG⁰_(aq)0″> and ΔG(n₂=0.175) are 3.31 and 4.30 K cal. mol^-1 respectively at 30⁰C and ΔG⁰ changes by 0.99 Kcal mol^-1 in the transfer reaction.

 

and this results in a change of 3.25 cal mol^-1 in entropy.

ΔpK_a^T (S-W) values i.e.,ΔpK_a^T (S)- ΔpK_a^T(W), [Where S and W refer to mixed solvents and water respectively] of thiobarbeturic acids at 30⁰C are given in Table – 4. The change in ΔpK_a^T(S-W) which is found to be different for the different acids for the same percentage of dioxane is probably due to the presence of different substituents which cause a great change in the distribution of electron density in the ring and hence the electron density at any particular point is also affected.

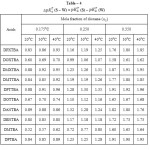Table 4  Click here to View table

 

Aknowledgment

The authors thank to Department of chemistry, Sahu Jain (P.G.) College, Nazibabad and R. S. M. (PG) College, Dhampur for providing the necessary facilities.

References

1. Haque .N., Roedel J. N.,. Lorenz I. P, Anorg. Z., Allg. Chem. 2009, 635,496 – 502.
2. Haque .N., Neumann. B., Lorenz I. P, Naturforsch. Z. 2010, 65 b, 101 – 106.
3. Haque. N., Neumann. B.,, Mayer. P., Lorenz. I. P., J. Organomet. Chem. 2010 manuscript in preparation.
4. Meusel. M., Ambrozak. A., Heckes. T. K., Gutschow. M., J. Org.Chem. 2003., 68, 4684.
5.  Brunner. H. , Ittner. K. P., Lunz. D., Schmatlock. S., Schmidt. T., Zabel. M., Eur. J. Org. Chem. 2003.,855,.
6. Chansah. E.,. Weiss. D. S, Neuropharmacology ., 2001.,40, 327,.
7. Wiessberger. A.  ,. Proskauer. E.S, Riddick. J. A.  and Toops. E. E., Jr. , Techniques of organic chemistry, vol. VII, Inter science, New York, 1955, p. 126.
8. Albert. A.  and Sergeant. E. P., Ionization constants of acids and bases. Methuen, London, 1963., p. 28.
9. Shukla. J. P. ., and Tandon, S. G., J. Inorg. Nucl. Chem., 1971.,33., 1681.
10. Van., L. G.  U₁ tert and Haas., C. G. .J. Am. Chem. Soc., 1953., 75 451.
11. Shukla. J. P. ., and Tandon. S. G., J. Electro anal. chem., 1972 .,75 423.
12. Harned. H. S.  and. Owen. B. B, The Physical Chemestry of electrolytic solutions, Ranhold, New York, edn. 1967., 3, pp 716.
13. A. Albert and E. P. Sergeant, Ionization constants of acids and bases, Methuen, London, p. 168(1962).
14. Agarwal. Y. K., Talanta, 1973.,  20., 1354.
15. Shukla. J. P,. Manchanda. V. K and Subramaniam. M. S., J. Electronal Chem., 1977.,40., 431.
16. Shukla. J. P.  and Subramaniam. M. S., Thermo Chem. Acta. , 1980., 35., 293.
17. Gurney. R. W., J. Chem. Phys., 1938., 6  499.
18. Sager. E. E., Robinson. R. A.  and Bates. R. G., J .Ras. Natl. Bur. stand. Sect. , A, 1965., 68.,  305
19. Gove. W. L. , statistical methods for chemical experimentation, Inter science, New York, Chap. VI. 1952., p. 127.
20. Harned .,H. S. and Owen. B. B. , The Physical Chemistry of electrolytic solutions, Rembold, New York, edn1952.,. 3. p. 756.
21. Robinson. R. A.  and Stokes. R. K., Electrolytic solutions, Butterworths, London, Table – 7, 1955., p. 541.
22. King. E. J., Acid base equilibrium, Pergamen, Oxford, p. 256 (1965).
23. Harned .,H. S. and Owen. B. B. , The Physical Chemistry of electrolytic solutions, Remhold, New York, edn. 1967, 3, p. 685.
24. Harned .,H. S. and Dedell. T. R., J. Am. Chem. Soc. 1941., 63., 3308.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.