Mathematical Study of Temperature Measurement by Thermocouple in Chemical Processes
Doctoral student, Azerbaijan State Oil and Industry University, Baku, Azerbaijan.
Corresponding Author E-mail: nabi.iskandarov@engineer.com
DOI : http://dx.doi.org/10.13005/ojc/380304
Article Received on : 05-Mar-2022
Article Accepted on :
Article Published : 16 Jun 2022
Reviewed by: Dr. Sadegh Parvizi
Second Review by: Dr. Munther Abdul-Jaleel Mohammed-Ali
Final Approval by: Dr.MGH Zaidi
Processing of oil, gas and gas condensate is one of the most widespread areas of modern chemical-technological processes. Due to the safety of chemical and technological process management, strict requirements have been set for the quality of processes in the oil and gas refining and petrochemical industries. During chemical-technological processes in the oil and gas industry, the fractional composition of the product, the typical boiling point, the octane number of gasoline, the cetane number of diesel fuel, the evaporation temperature, the ignition temperature and other parameters must be determined with special accuracy. This set of characteristics is used in the laboratory assessment of the quality of oil, oil products and gas condensate. Temperature measurements performed during such processes must have maximum accuracy. For this reason, the determination of temperature by thermocouples in the above-mentioned chemical processes has been mathematically studied and evaluated during the research.
KEYWORDS:Accuracy; Chemical Processes; Temperature Measurements; Thermodynamics, Metrology
Download this article as:| Copy the following to cite this article: Iskandarov N, Mathematical Study of Temperature Measurement by Thermocouple in Chemical Processes. Orient J Chem 2022;38(3). |
| Copy the following to cite this URL: Iskandarov N, Mathematical Study of Temperature Measurement by Thermocouple in Chemical Processes. Orient J Chem 2022;38(3).Available from: https://bit.ly/3mPS19C |
Introduction
Currently, the petrochemical industry is one of the most important areas of production processes. Almost 500 types of chemical products are obtained from oil, and the most important of these oil products are motor and aviation gasoline, kerosene, jet and diesel fuels, fuel oil and other petroleum products, gas condensates, various solvents, etc. such as liquid fuels. Many methods and measurement tools are used to obtain measurement information on the physical and chemical properties of petroleum products, oil and gas condensates, and the amount and composition of individual components. In practice, the measuring instruments used to determine the quality of oil and oil products, especially the fractional composition of a multicomponent mixture, refer to the thermal, ie thermodynamic temperature measuring instruments of analytical techniques [1].
The fractional composition of a multicomponent mixture means the dependence of the boiling point of the individual fractions on the sample of the analyte or the amount of these fractions in the samples of the analyte depending on their boiling point. In order to obtain information on the composition of the fraction, the method of expulsion of the analyzed substance at atmospheric pressure according to the boiling point is used. The composition of the fraction is one of the main and most important indicators of quality of petrochemical and chemical products – gasoline, kerosene, jet and diesel fuels, oil fuel and other petroleum products, gas condensates, various solvents and other products [2].
The measurement of these parameters used in laboratory practice, the temperature measurements performed during these processes and the determination of errors in the measurements performed are considered to be one of the main factors influencing the results of the chemical-technological process. For this reason, the numerical evaluation of thermodynamic temperature measurements carried out by thermocouples in chemical-technological processes is considered an important and relevant example of research.
Materials and Methods
As we have mentioned, in practice, many means of measuring the quality of oil and oil products belong to the thermodynamic temperature means of analytical techniques. Reducing errors due to internal and external influences is one of the most pressing issues in measurement techniques. During the research, the determination of the ignition temperature of oil and oil products by the standard method was studied numerically, mathematical jumps during temperature measurements were identified and the importance of maximum accuracy of temperature measurements performed in such chemical processes was assessed.
The following materials, equipment and tools were used during the research:K-type thermocouples, 2 pieces, Model: WRNK-387;
Mini Portativ İnverter, Benzin Generatoru, LG1300I (800 W);
Temperature Controller, Made of Put into A – 50 oC ~ 110 oC Install Embedded Digital Thermostat Controller, Model: XH-W1209;
Mini Heater Matrix, Part no: TAMAU6083;
Stylized metal pipe, inner diameter 20 mm;
Filter block, cocount carbon material, 5 x 5 x 10.8 inches;
Laminar Flow Cabinet, BBS-V500, External Size (W=550 mm, D=460 mm, H=700 mm);
Liquid oil, ρ = 0,8-0,9 g/cm3.
During the research, it was determined that the ignition thermodynamic temperature is the temperature of the liquid at which temperature, under certain conditions, its vapors are mixed with air during heating, and the ignition process occurs when a flame is presented to it. Under the conditions of heating liquid oil products, the amount of their vapors in the “air-vapor” mixture increases with the formation of oil on the surface. An explosion occurs when the flame is introduced into the mixture, and the next combustion of the oil product does not occur due to the absence of its vapors in the air after the explosion. The ignition process for different petroleum products takes place in the “air-vapor” mixture at the same volume and constant pressure concentrations of vapors. Currently, the ignition thermodynamic temperature is a normalized quality indicator of lubricants, diesel, jet and automotive fuels, gasoline solvents and other products. This quality indicator is considered to be the most frequently defined indicator in oil refineries. The composition of fractions with low boiling point in the oil product is determined by the ignition temperature. This indicator also characterizes the danger of burning oil products. The decrease in the ignition temperature corresponds to an increase in the concentrations of light fractions and an increase in the fire hazard of the oil product. The ignition temperature is determined by analysis in an open or closed loop. The closed-loop analysis method gives more accurate and reliable results, as well as results that remain stable over a similar interval. Therefore, it is widely used automatic ignition temperature analyzers (Figure 1).
 |
Figure 1: Scheme of automatic ignition temperature analyzer. Click here to View figure |
During the operation of the device shown in Figure 1, the analyte enters the primary heater at a constant flow (approximately 0,5 m/s) rate from the preparation unit, and the analyte at the outlet is mixed with a constant volume flow of air from the preparation unit. The resulting mixture enters the main heater and the ignition chamber. If the temperature of the mixture entering the chamber reaches the ignition temperature, then the steam-air junction is ignited periodically (at intervals of 7 seconds) by electric sparks generated in the candles during the transmission of high-voltage voltage.
The flame in the ignition changes the temperature in the vapor space of the chamber and is absorbed by this thermoelectric sensitive element. The signal of the element is transmitted to the control unit, which opens the power supply of the main heater. The heater is switched on soon after the ignition spark. If several ignition processes occur continuously and sequentially, the heater remains open. The heater is switched on after the first spark, ie when the ignition process does not occur. Thus, the value of the thermodynamic temperature at which the analyte is ignited in the chamber, the “air-vapor” mixture, is automatically captured. The thermodynamic temperature of the analyte in the chamber is measured by a thermoelectric sensitive element and the signal is received by an electronic potentiometer or a normalizing converter. The numerical value obtained is an important factor in the implementation and management of the chemical process. We can even say that the next steps of the chemical process are regulated by this numerical value [3].
The accuracy and precision, as well as the consistency of the thermodynamic temperature unit are of great importance in the measurements. It should be noted that the errors that occur during the measurements are within the allowable range. When the error interval at the set values is higher than the allowable error interval, it is recommended to replace or calibrate the temperature measuring instruments used during the chemical process.
Results and Discussion
Accuracy problem and solutions of thermocouples used in chemical processes
When determining the ignition temperature in chemical processes, the temperature change that occurs during the reaction of reagents with air is one of the most important factors that significantly affect the outcome of the chemical process. The effect of temperature on the reagent-air exchange during the reaction has been demonstrated in both theoretical and experimental studies over the years. However, the study of temperature changes in reagent-air exchange during experimental and theoretical studies has been discussed for a long time. Although many researchers have noted in the discussions that changes in the direction of temperature increase during exchange are (TAI > TRI), some researchers have taken a different approach and noted that the process is reversed (TAI > TRI).
In recent years, in all theoretical and experimental research on temperature changes during reagent-air exchange, thermocouples have been preferred to measure ambient temperature. When using these measuring instruments based on the determination of voltage differences, it is necessary to calibrate the sensitive element to increase the accuracy of the conversion factors between temperature and voltage when the device is immersed in the environment. When measuring the temperature of an object with temperature Tf when using a thermocouple, the temperature of the medium used for calibration at Tf is the same as the temperature of the junction where the 2 different wires are connected. In addition to the above-mentioned factor in the measurement of ambient temperature during reagent-air exchange, two other problems that need to be studied are also relevant today. One of them is that the relatively large reference point of the thermocouple can make it difficult to measure the temperature in the surface layer. Another problem is the errors that occur during the exchange between molecules and the sensitive element of the thermocouple due to unforeseen effects during the measurement, and during the collision of molecules in the direction of the reagent-tin-air. These collisions create an unequal difference between the reagent and the air temperature. The difference is reflected in a shorter range within normal environmental conditions. It has not yet been investigated whether this inequality could be a source of uncertainty when the process is likely to take place under abnormal environmental conditions [4].
The small inclinations that can occur during temperature measurements in chemical processes depend significantly on the simplification and mathematical modeling of the system under normal environmental conditions in which the measurements are performed. To model this system, the thermal equations of thermocouple, liquid, and air exchange, as well as the heat and molecular displacements in the reagent, must be mathematically studied and solved under appropriate conditions. The obtained results are widely used to assess the role of thermocouples in determining surface inclinations during the study of temperature differences in reagent-air exchange.
The biggest problem with measuring temperature in reagent-air exchange during thermocouple temperature measurements in chemical processes is to determine the difference between the temperature determined by the measurement and the actual poplar temperature, despite the calibration of the sensitive element that measures the temperature of the reagents at Tf. Determining this difference is an important nuance, especially in the air phase for several reasons. The first is the effect of thermocouple performance on thermal conductivity through wires. As previously shown, the thermal conductivity of all phases determines the temperature distribution in liquids and solids. Because the thermal conductivity of metals is much higher than that of liquids, heat can be more easily dissipated through liquids than wires, and the temperature of the sensitive element can differ significantly from the temperature of the surrounding liquid. Another is that the movement of molecules under abnormal environmental conditions can limit the thermal balance between the reagent and the air and lead to a wide range of errors during exchange. The latter, during the experiments, we observed that the result provided by the sensitive element can easily change due to the vibrations that can occur during the exchange. For this reason, it is more appropriate to maintain a small distance between the sensitive element and the medium when measuring the interfacial temperature during reagent and air exchange. If this distance is large, the reagent will stick to the sensitive element and cause errors during the reaction with air. It should be noted that even if the sensitive element does not come into contact with the reagent, it can impair the accuracy of the results obtained simply by participating in the exchange. Taking into account all the factors mentioned, we can determine the surface temperature of the reagent and air
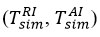
from the simulation [5].
To determine the effect of thermocouples on temperature inclinations during temperature measurements in chemical processes, Figure 2 shows a diagram comparing experimentally determined inclinations
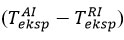
and predicted inclinations
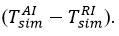
 |
Figure 2: Comparison of experimental and predicted temperature inclination. |
It can be seen from the graph that the predicted tendencies for all experiments move in one direction, ie the predicted tendencies have a smaller error than those measured experimentally by the thermocouple. The closest ratio to the inclination during the exchange (assuming σT = 1) is 0,681. This correlation means that temperature inclinations are overestimated by at least 33,0 % due to errors in the thermocouple during reagent-air exchange, and that the theoretical inclination results should be 68,1 % of those measured in experiments. The comparative energy placement coefficient we have described is based on the results of the exchange, assuming that σT is equal to 1. This result is also the most important nuance that ensures that the molecules are reflected in a completely diffuse manner in the surface layer [6].
As σT decreases during exchange, the temperature obtained from the measurement differs in a wider range from the temperature inclination measured experimentally with the thermocouple. We can determine the modeled temperature inclination when the sensitive element of the thermocouple is 5,5 mm above the center point of the exchange. In the presented graph, the range of the largest point of the simulated temperature inclination is shown in green, and the range of the smallest point is shown in purple, as the error lines vary between 0,5 and 30,0 mm around the exchange area of the thermocouple. Here, the minimum and maximum points of the installed lines for x = σT are 0,634 and 0,708, respectively, and for σT = 0,719 are 0,441 and 0,512, respectively [7].
While the modeled interfacial temperatures
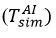
in reagent-air exchange play an important role in the speculative reflection of air molecules (σT<1), the thermocouple
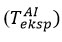
goes far beyond the temperature predicted in the experimental study. From the presented graph, it can be seen that as σT decreases from 1,000 to 0,725, the inclinations that occur during the simulation of the exchange become smaller, which makes the sensitive element more receptive to the ambient temperature. In this case, smaller values of temperature inclinations can be balanced by adding σT. The smallest area in each part mentioned here varies according to the farthest distance (≈30,0 mm) from the exchange center of the thermocouple [8].
It is clear from the research that the thermocouple cannot read the interfacial temperatures with full accuracy during air-reagent exchange. This is because environmental factors that can affect the measurement result, errors in the method, incompetence of the staff and defects in the equipment can lead to incorrect estimates of the measurement result and deviations within a certain range. Therefore, it is necessary to determine whether the current propensity of thermodynamic temperatures predicted from modeling is consistent with CTG, NET and SRT. It has previously been shown that the expression NET is not related to the interfacial temperature during reagent-air exchange. The comparison of the results obtained from numerical modeling, taking into account the temperature inclination coefficients predicted by the CTG and all the factors (especially atmospheric pressure) influencing it, is described in Table 1 below. As noted in the table, the temperature trends studied are still many times greater than those calculated from the CTG [9].
Table 1: A comparison between the inclination estimated by the experimental and simulated CTG.
|
Exp № |
PAexp (Pa) |
Experimental inclination (oC) |
σr = 1,000 |
σr =0,725 |
Inclination estimated by CTG (oC) |
|
1 |
461,0 ± 12,5 |
1,79 |
1,41 |
0,93 |
0,08 |
|
2 |
469,5 ± 12,5 |
3,68 |
2,79 |
2,12 |
0,21 |
|
3 |
472,4 ± 12,5 |
6,92 |
6,41 |
3,18 |
0,42 |
|
4 |
469,2 ± 12,5 |
10,59 |
9,22 |
6,65 |
0,65 |
|
5 |
414,0 ± 12,5 |
9,95 |
7,03 |
5,98 |
0,51 |
|
6 |
406,0 ± 12,5 |
19,82 |
12,64 |
8,53 |
0,78 |
|
7 |
208,7 ± 12,5 |
28,13 |
18,95 |
13,24 |
1,51 |
In the study, we followed the procedure shown in the formulas to assess the compatibility of SRT with normalized temperatures in the direction of reagent-air exchange, and used the predicted values of interfacial temperatures
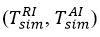
and local flow
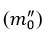
to predict environmental conditions. As shown in Table 2, only small changes in SRT-calculated pressures were observed during the study, and all abnormal environmental conditions, even atmospheric pressure values, fell within the experimental uncertainty of the measuring instrument [10, 11].
Table 2: Estimated pressures of simulated surface temperatures with corrected and uncorrected SRT.
|
Exp № |
PAexp (Pa) |
PASRT (Pa) |
PASRT (Pa) |
|
1 |
461,0 ± 12,5 |
462,4 |
475,5 |
|
2 |
469,5 ± 12,5 |
473,1 |
479,1 |
|
3 |
472,4 ± 12,5 |
471,0 |
465,8 |
|
4 |
469,2 ± 12,5 |
475,3 |
473,1 |
|
5 |
414,0 ± 12,5 |
560,3 |
471,7 |
|
6 |
406,0 ± 12,5 |
586,3 |
573,8 |
|
7 |
208,7 ± 12,5 |
294,2 |
280,3 |
Table 3: Three selected experimental conditions close to the evaporating drop.
|
Exp № |
TAtc (oC) |
TB (oC) |
ra (mm) |
rD (mm) |
rB (mm) |
TAİ |
TRİ |
Temperature |
|
1 |
25,65 |
25,32 |
5,95 |
0,71 |
26,00 |
23,56 |
22,20 |
1,36 |
|
2 |
25,63 |
25,00 |
5,63 |
0,82 |
26,00 |
23,64 |
23,09 |
0,55 |
|
3 |
25,59 |
25,00 |
5,18 |
0,60 |
26,00 |
23,52 |
23,01 |
0,51 |
Reduction of errors in thermocouple measurements
As mentioned, the main reason for the numerical evaluation of thermodynamic temperature measurements by thermocouples in chemical-technological processes is to minimize errors in thermodynamic temperature measurements by thermocouples. A graphical representation is shown in Figure 3 to better understand the procedure for solving the problem posed during the research. The research used an innovative method to find the appropriate
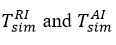
values for each experiment. In modeling the solution of the problem,
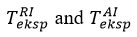
temperatures based on real experience were used to calculate the interfacial temperatures in the reagent-air exchange corresponding to each simulation [12-15].
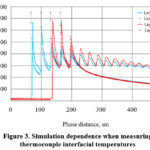 |
Figure 3. Simulation dependence when measuring thermocouple interfacial temperatures. |
When the thermocouple was in a liquid, it was necessary to calculate
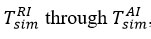
since the unwetted part of the thermocouple exchanged heat with steam. Therefore, it began with the discovery of an iterative solution
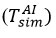
, which is considered an important condition for performing a mathematical evaluation. In steam, the edge of the roller is up to 5,5 mm close to the interface so that the roller is 18,0 mm above the central interface. For simulation, the thermocouple in the reagent is assumed to be at the same distance from the exchange site. In this case, the initial value for
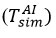
was taken and
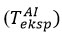
was changed until the experimentally measured temperature in the air was equal [16-19].
The thermocouple was then moved 3,5 mm above the area where the experimental temperature was known, and the temperature at the upper boundary was changed until the value of Tout was equal to the experimental value at 3,5 mm of the temperature of the sensitive element. The thermocouple was moved back and forth between these two reference points. The
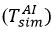
and Tout values were updated repeatedly for each simulation until no additional change was observed in
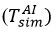
and Tout. In this case,
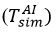
was taken as the interfacial temperature by the air. During the study, calculated air temperatures were used to find
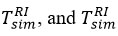
was found in a repetitive form, similar to air temperatures [20-21].
Conclusion
During the research, the behavior of the thermocouple measuring the interfacial temperatures in the reagent-air exchange was mathematically studied. During the study, density and temperature distribution in liquids, as well as air temperature distribution were observed using the appropriate density and reagent-air temperature inclination conditions. The final temperature effect of thermal conductivity and thinning of molecules using electrically conductive wires was taken into account. The reagent and the interfacial temperatures in the air were found to be innovative from the simulation. The results showed that the result of the thermocouple reading of the interfacial temperature in the reagent is very close to the surface temperature of the reagent. Thermocouple readings in the air mutually confirmed the results of the exchange temperatures due to heat transfer to the junction point via thermocouple wires, inaccessibility of simulation due to experimental limitations, and thinning of molecules. Finally, the corrected and simulated temperatures were applied to the SRT expression.
Acknowledgement
The author Nabi Iskandarov is thankful to Ph.D, Assoc.Prof. Shamo Tapdigov (State Oil Company of Azerbaijan Republic, Oil Gas Research Design Institute) for affording scientific assistance to this research work.
Conflicts of interest
The author declares that there is no conflict of interest in the present research work.
Funding sources
There are no funding Sources.
References
- Al-Nuaimi, I. A.; Bohra, M.; Selam, M.; Choudhury, H. A.; El-Halwagi, M. M.; Elbashir, N. O. Optimization of the aromatic/paraffinic composition of synthetic jet fuels. Chem. Eng. Technol. 2016, 39, 2217–2228.
CrossRef - Webster, E. and Saunders, P. Characterizing drift behavior in Type S thermocouples to predict in-use temperature errors. Int. J. Thermophys 2019, 41, 5.
CrossRef - Bayramov, M. R.; Hajiyev, M. M.; Mirzayeva, M. R.; Mammadov, I. Q. Workshop on petrochemistry and petrochemical synthesis (textbook) 2018, 1, 201.
CrossRef - Arif A. R.; Ying S. Probing the temperature profile across a liquid-vapor interface upon phase change.The Journal of Chemical Physics 2020, 42, 153.
- Isgandarzada E. B.; Aslanov Z. Y. Methods and means of measurement and control 2017, 1, 176.
- Wang, X.; Jia, T.; Pan, L.; Liu, Q.; Fang, Y.; Zoul, J.; Zhang, X. Review on the relationship between liquid aerospace fuel composition and their physicochemical properties. Trans. Tianjin Univ. 2021, 27, 87–109.
CrossRef - Grazia, L.; Christoph S.; Bernhard, W. On the importance of kinetic effects in the modelling of droplet evaporation at high pressure and temperature conditions, Research Gate 2020, 22, 272.
- Tucker, D.; Andreu, A.; Elliott, C.; Ford, T.; Neagu, M.; Machin, G. and Pearce, J. Integrated self-validating thermocouples with a reference temperature up to 1329 °C. Meas. Sci. Technol 2018, 29,1–9.
CrossRef - Mohammad, A. K.; Nobes, D. Effect of the thermocouple on measuring the temperature discontinuity at a liquid-vapor interface, Research Gate 2017, 26, 8.
- Yun, S. J.; Abidov, A.; Kim, S.; Choi, J. S.; Cho, B. S.; Chung, S. C. Water vapor transmission rate property of SiNx thin films prepared by low temperature (<100 C) linear plasma enhanced chemical vapor deposition. Vacuum 2018, 148, 33–40.
CrossRef - Webster, E. Trials of Pt-20 %Rh vs. Pt thermocouples between 157 °C and 962 °C. Metrologia 2020, 57, 47-49.
CrossRef - Claucherty, S.; Sakaue, H. An optical-chemical sensor using rhodamine B on anodized-aluminum for surface temperature measurement from 150 to 500 K. Sens. Actuators B Chem. 2017, 240, 956–961.
CrossRef - Vozka, P.; Modereger, B.; Park, A.; Zhang, W.; Triced, R.; Kenttämaa, H.; Kilaz, G. Jet fuel density via GC×GC-FID. Fuel 2019, 235, 1052–1060.
CrossRef - Kim, Y.; Lee, Y. and Joung, W. Temperature dependence of the thermoelectric inhomogeneity for Type B thermocouples from 180 °C to 960 °C. Meas. Sci. Technol 2017, 28, 24–26.
CrossRef - Webster, E.; Greenen, A. and Pearce, J. Inhomogeneity in Type B and Land-Jewell noble-metal thermocouples. Int. J. Thermophys 2016, 37, 70.
CrossRef - Pearce, J.; Edler, F.; Elliott, C.; Greenen, A.; Harris, P.; Izquierdo, C.; Kim, Y.; Martin, M.; Smith I.; Tucker, D. and Veltcheva, R. A systematic investigation of the thermoelectric stability of Pt–Rh thermocouples between 1300 °C and 1500 °C. Metrologia 2018, 55, 558–567.
CrossRef - Webster, E. Thermal preconditioning of MIMS Type K thermocouples to reduce drift. Int. J. Thermophys 2016, 38, 25-26.
CrossRef - Webster, E. Drift in Type K bare-wire thermocouples from different manufacturers. Int. J. Thermophys 2017, 38, 70.
CrossRef - Rodiet, C.; Remy, B.; Degiovanni, A. Optimal wavelengths obtained from laws analogous to the wien’s law for monospectral and bispectral methods, and general methodology for multispectral temperature measurements taking into account global transfer function including non-uniform emissivity of surfaces, Infrared Phys. Technol 2016, 76, 444–454.
CrossRef - Hreha, P.; Radvanska, A.; Knapcikova, L.; Legutko, S.; Krolczyk, J.; Hloch, S.; Monka, P. Roughness parameters calculation by means on-line vibration monitoring emerging from AWJ interaction with material. Metrology and Measurement Systems 2016, 22, 315-326.
CrossRef - Nurfatihah, J.; Jesbains, K.; Pandey, A.; Shahabuddin, S.; Hassani, S.; Saidur, R.; Rasit, R.; Azwadi, N.; Naim, M. A Review on Nano Enhanced Phase Change Materials: An Enhancement in Thermal Properties and Specific Heat Capacity, Journal of Advanced Research in Fluid Mechanics and Thermal Sciences, 2019, 57, 24-28.

This work is licensed under a Creative Commons Attribution 4.0 International License.










