Modified Rate Law for Bimolecular Reactions: Applicable to Surface as well as Non-Surface Reactions

Introduction

The rate law is the center of all rate expressions for non-surface reactions. The core of the rate law is embedded in kinetic theory of collisions with the assumption that fraction of collisions having enough energy leads molecular vibration and thereafter breaking/forming of new bonds¹. Simply for a second order reaction, rate is directly proportional to different concentration of reactants.

If surface reactions are included, the rate of reaction can be broadly assigned as interaction between two adsorbed chemical species (on catalyst surface) or interaction between adsorbed species (on catalyst) and non-adsorbed species (expressed in term of concentration/pressure) or interaction between non-adsorbed species in the reaction mixture. For the first case, interaction between the two adsorbed species can be shown by product of surface coverage of both different species over the catalyst surface as shown in Scheme 1(1). For second case, interaction between one adsorbed and one non-adsorbed species can be shown by product of surface coverage of one species over the catalyst site and concentration of another species in the reaction mixture as shown in Scheme 1(2). For third case, interaction between non-adsorbed species can be viewed by product of concentration of both species and very likely as rate law discussed in right hand side expression of Scheme 1(3) as well as in eq (1).

Scheme 1: (1) The adsorbed “A” and adsorbed “B” undergoes into a reaction (2) The adsorbed “A” undergoes into a reaction with non-adsorbed “B” (3) Two non-adsorbed  “A” and “B” undergo into a reaction. Click here to View scheme

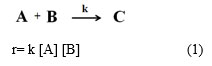
r = k θ_A θ_B                                                    (2)

r = k θ_A [B]                             (3)

r = k [A] [B]                            (4)

The first case or Scheme 1 (1) shows purely surface reaction and it should be dealt with Langmuir adsorption isotherms^2,3.  First of all reactants “A” and “B” are adsorbed on uniform catalyst surface having K_A and K_B equilibrium constant of adsorption-desorption respectively. Further both adsorbed species interact and undergoes into a reaction having rate constant “k” as shown in scheme 1 (1). The surface coverage of each reactant can be derived by solving the equation of rate of adsorption (v_a) as well rate of desorption (v_d) which are reversible to each other. The rate of adsorption of a species is proportional to the concentration/pressure of species in the liquid/gas phase respectively as well as fractional of the surface that is bare/uncovered (θ_o). The total catalytic active sites are 1 (1 = fraction of surface uncovered (θ_o) + fraction of surface covered (θ_{reaction species}) by each species). So, overall rate of adsorption of species A and B can be expressed as equation 5 & 7 respectively. Again the rate of desorption is proportional to fraction of surface covered (θ_{reaction species}) by adsorbed species as equation 6 & 8.

v_a^A = k_a [A] (1- θ_A – θ_B)               (5)

v_d^A = k_d θ_A                                                  (6)

 v_a^B = k_a [B] (1- θ_A – θ_B)              (7)

v_d^B = k_d θ_B                                                   (8)

As adsorption and desorption are reversible processes, equilibrium constant comes in existence. Further equations (5-8) are solved and two equations having two unknown (θ_A and θ_B) are derived and solved. Finally, value of θ_A  and θ_B can be put in eq (1) and then rate equation becomes as

 r = k K_A [A] K_B [B]/(1+ K_A [A]+K_B [B])²                        (9)

Overall the calculation of surface coverage needs the idea of many adsorption deadsorption expressions and its solutions. As well as surface conditions vary, solutions of equation becomes tougher i.e. the product “C” may also initiate reversible reaction, reactant may adsorbed nonequivalent surfaces of the catalyst etc. So, it is needed to present some law which is simpler as rate law as well as which can satisfy both surface and non-surface reactions. Herein, a modified rate law applicable to convention as well as surface reaction is proposed.

Modified rate law for surface and non-surface reaction

The equation (9) can be explained in three parts as mentioned below;

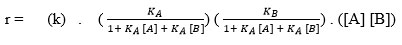
It should be noted that first part “rate constant”, second part is expressions related to “surface adsorption and surface deadsorption phenomena of reactant A and B” and third part “product of reactants concentration” remain intact as rate law. We termed the second section as surface affairs of reactant A (termed as Ω_A) and surface affairs of reactant B (termed as Ω_B) respectively. So, now the above expression can be written as

r =      (k)   .   Ω_A  Ω_B . ([A] [B])

r = k Ω_A[A] Ω_B[B]                                                  (10)

So, the modified rate law for bimolecular reaction over (applicable to surface and non-surface reaction) can be stated as “Rate of a reaction is directly proportional to concentration as well as catalyst surface affair of each reactant”. Where catalyst surface affair (Ω) of “i^th” species is defined as

Ω_i = K_i/(1+K_i[i] + K_j[j] + …)                      (11)

Where K_i is the equilibrium constant of “i”species for adsorption-desorption processes over catalyst.  i, j, k,… indicates the different adsorbed chemical species at uniform catalyst sites and the same [i], [j], [k],… indicates the concentration of different adsorbed chemical species at uniform catalyst sites. So in the catalyst surface affairs of one species, there will be contributions of another species also which are adsorbed on uniform catalyst sites (as “i” and “j” species are adsorbed on metal atom sites of catalyst).

The equation (11) can be presented as described below.

So, for a reaction pattern where reactants A and B are adsorbed on uniform catalyst surface (Langmuir-Hinshelwood uniform surface ^4,5 and then adsorbed species undergo for a reaction and liberates product C as presented below.

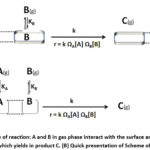Figure 1: (A) Scheme of reaction: A and B in gas phase interact with the surface and then undergoes a reaction which yields in product C. (B) Quick presentation of Scheme of reaction. Click here to View figure

Then catalyst surface affairs of A and B species are defined as

Ω_A = K_A/(1+K_A[A] + K_B[B])                                                   (12)

Ω_B = K_B/(1+K_A[A] + K_B[B])                                                   (13)

So, rate of surface reaction can be found by putting equation 12 and 13 in modified rate equation,   r = k Ω_A[A] Ω_B[B]

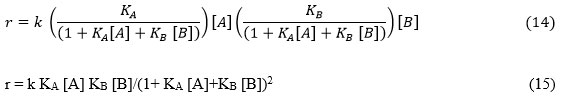
Synthesis of ammonia by N₂ and H₂ over Fe₂O₃ catalyst is the simplest example of Langmuir-Hinshelwood uniform surface reaction. H₂ and N₂ are adsorbed dissociately over catalyst surface and then adsorbed atomic species “H” and “N” undergo reaction and liberate ammonia.

Case I. If product (C) will form and subsequently C interacts with the catalyst surface having adsorption phenomena. Then catalyst surface affair of reactant A and B are modified as below.

Figure 2: (A) Scheme of reaction: A and B in gas phase interact with the surface and then undergoes a reaction which yields in product C. C again undergoes adsorption- deadsorption interaction with catalyst surface (B) Quick presentation of Scheme of reaction. Click here to View figure

Ω_A = K_A/(1+K_A[A] + K_B[B] + K_C [C])                                 (16)

Ω_B = K_B/(1+K_A[A] + K_B[B]+ K_C [C])                                  (17)

So, rate of surface reaction can be finding by putting equation 15 and 16 modified rate equation, r = k Ω_A[A] Ω_B[B]

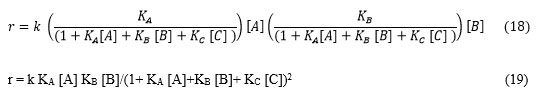
Case II. If product (C) will be adsorbed on uniform catalyst sites and further involve in reverse reaction. This time not only catalyst surface affairs of reactant A and B will be modified but also new affairs of C with catalyst surface should also be considered. The rate of reaction can be expressed as below: 

r = k₁ Ω_A[A] Ω_B[B] – k_-1 Ω_C[C]                                       (20)

Scheme 2 Click here to View scheme

Ω_A = K_A/(1+K_A[A] + K_B[B] + K_C [C])                              (21)

Ω_B = K_B/(1+K_A[A] + K_B[B]+ K_C [C])                                 (22)

Ω_C = K_C/(1+K_A[A] + K_B[B]+ K_C [C])                                   (23)

So, rate of surface reaction can be found by putting equation 21-23 into equation 20.

r = {k₁ K_A [A] K_B [B]/(1+ K_A [A]+K_B [B]+ K_C [C])²}- {k^-1 K_C [C] /(1+ K_A [A]+K_B [B]+ K_C [C])²}                                                (24)

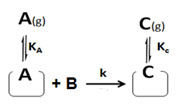
Case III. If a reactant (say B) from the gas/solution reacts with an adsorbed reactant (say A) without adsorbing itself on the surface as in Eley-Rideal process⁶. This time non-adsorbed reactant (B) had no surface affairs on catalyst surface and so catalyst surface affairs of non-adsorbed reactant (B) should be removed from equation 10. Then the new rate expression will be as below:

r = k Ω_A[A] [B]                             (26)

Ω_A = K_A/(1+K_A[A] + K_C [C])                           (27)

So, rate of surface reaction can be found by putting eq (26) into eq. (27).

r = k K_A [A] [B]/(1+K_A[A] + K_C [C])                (28)

Hydrogenation of gaseous ethylene molecule by adsorbed hydrogen over Ni surface, The esterification of “chemosorbed 1-hexene” with “heptanoic acid in bulk” over Amberlyst catalyst and the dimerization of chemisorbed alkene C8 and C24 linear alkenes in liquid phase over Amberlyst catalyst follow Eley-Rideal kinetics.

Hydrogenation of gaseous ethylene molecule by adsorbed hydrogen over Ni surface ⁷, The esterification of “chemosorbed 1-hexene” with “heptanoic acid in bulk” over Amberlyst catalyst⁸ and the dimerization of chemisorbed alkene C8 and C24 linear alkenes in liquid phase over Amberlyst catalyst follow Eley-Rideal kinetics.⁹

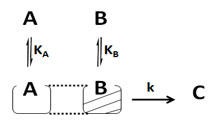
Case IV. Another possibility may be that reactants (A and B) adsorbed on non-uniform surfaces of the catalyst (respect to each other catalyst sites) or adsorbed at different sites of catalyst in close proximity (Langmuir-Hinshelwood non-uniform surface). Here, at one uniform catalyst surface only one species is adsorbed. So, in the catalyst surface affairs of one species, there will be no participation of another species which is adsorbed on different sites/non-uniform sites. The parts of catalyst which adsorb “i” species are different from those which adsorb “j” species.

The rate of reaction can be expressed as below: 

r = k Ω_A[A] Ω_B[B]                                                   (29)

Ω_A = K_A/(1+K_A[A])                                                      (30)

Ω_B = K_B/(1+K_B[B])                                                             (31)

So, rate of surface reaction can be found by putting eq (30& 31) into eq. (29)

r = k K_A K_B [A] [B]/{(1+K_A[A]) (1+ K_B [B])}                       (32)    

The reaction between hydrogen and nitrous oxide on gold¹⁰ and reaction between hydrogen and carbon dioxide on tungsten¹¹ are examples of such kinetics. Two gases H₂ and N₂O are adsorbed independently over gold, they react and form H₂O and N₂.  In the same way, two gases H₂ and CO₂ are adsorbed independently over tungsten, they react and form H₂O and CO.

Case V. If neither’s of reactants have catalyst surface affair or both reactants are simply interacting and finally gives the product C. Then, catalyst surface affairs of reactants A and B should be removed from equation 10. This time, the rate of reaction is same as rate law for second order reaction as equation (1).

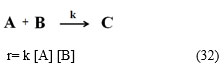
Conclusion

It can be concluded that the modified rate law for bimolecular reaction is easier and equally applicable to both surface reaction and non-surface reaction. Along with normal non-surface reaction, all the case of surface reaction based on Langmuir-Hinshelwood uniform surface treatment, Eley-Rideal and Langmuir-Hinshelwood non-uniform surface treatment can be derived easily within couple of steps.

Acknowledgement

G. G. Bhagavanbhai acknowledges Administration of Sankalchand Patel University Gujarat, India for providing continuous research support. RK acknowledges Indus University for supporting research.

Conflict of Interest

The authors declare that they have no known financial interests with the work reported in this paper.

Funding Sources

There is no funding source.

References

1. Harteck, P.; Zeitschrift für Physikalische Chemie., 1928, 139, 98-106
   CrossRef
2. Langmuir, I. Journal of the American Chemical Society., 1916, 38, 2221-2295.
   CrossRef
3. Langmuir, I. Journal of the American Chemical Society., 1918, 40, 1361-1403
   CrossRef
4. Langmuir, I. Transactions of the Faraday Society., 1922, 17, 621-654
   CrossRef
5. Hinshelwood, C. N.  Clarendon Press, Oxford, England, 1926, 145
   CrossRef
6. Rideal, E. K. Proceedings of the Cambridge Philosophical Society., 1939, 35 130; Eley  D. D.; Rideal, E. K. Proceedings of the Royal Society of London. Series A., 1941, 178, 429-451.
   CrossRef
7. Rideal, E. K. XXXIX.  Journal of the Chemical Society., 1922, 121, 309-318
   CrossRef
8. Gee, J.C; Fisher, S. Journal of Catalysis 2015, 331, 13-24
   CrossRef
9. Gee, J. C; Williams, S. T. Dimerization of linear olefins on Amberlyst® 15: Effects of chain length and double-bond position. Journal of Catalysis 2013, 303, 1-8
   CrossRef
10. Hutchison, W. K.; Hinshelwood, C. N. CCI. The interaction of hydrogen and nitrous oxide on the surface of gold. Journal of the Chemical Society., 1926, 129, 1556-1559
    CrossRef
11. Hinshelwood, C. N.;  Prichard C. R. CCVI. The interaction of carbon dioxide and hydrogen on the surface of tungsten. J. Chem. Soc., Trans., 1925, 127, 1546-1552 
    CrossRef

---

This work is licensed under a Creative Commons Attribution 4.0 International License.