Conductance, Dissociation Constant and Thermodynamic Parameters Studies of Succinic Acid in Water +PC and Water + THF Medium

Introduction

In continuation our earlier studies ^1-3 we focused in the present studies that how succinic acid solvated in water +PC and water + THF medium. Researchers interested in different weak acids in different solvent medium.

Study of conductance behaviour of aqueous and non-aqueous medium is much interest in recent past ^4-6.

As succinic acid is weak electrolyte, to determine limiting molar conductance was not measured by Onsagar equation. To determine limiting molar conductance we use Karus-Bray conductivity equation.

Many researchers studied the effect of different salts and weak acids in different solvent systems^7-15.

Our main objective to study to evaluate limiting molar conductance using Karus-Bray equation and also evaluate thermodynamic parameters for supporting the ion-solvation interaction system with this weak acid.

Experimental

Materials

Succinic Acid (Merck), PC (LOBA Chemicals), THF(PDFCL, Mumbai) were used as such, without any further purification.

Solutions Preparation

The solution of Succinic Acid in water and different compositions (10%, 20%, 40%, 50%, 60%, 80%) were prepared. Succinic Acid solution (0.1M) was prepared in water, water+PC and water +THF in volume ratio(v/v).

Result and Discussion

Molar conductance data was observed in different composition of succinic acid solution with (water+PC) and (water+THF). As succinic acid is weak electrolyte, to determine limiting molar conductance was not measured by Onsagar equation. To determine limiting molar conductance we use Karus-Bray conductivity equation.

The equation is 1/λm = 1/λm⁰ + λmc/λ_m⁰² kc  ——- (i)

Where Kc =dissociation constant, C = conc. in mol/ dm³,  lm⁰= molar conductance at infinite dilution.

If we plot 1/lm vs. lmC, we get l_m⁰ value from the intercept and from the slope, we can calculate Kc(dissociation constant).

Table 1 shows the the physical property data of the solvents PC and THF respectively.

Ka(association constant)’s were calculated from the limiting molar conductivities. Knowing the value of degree of association (α) , Ka value can be easily calculated. With increase in Ka value, degree of dissociation decreases. With increase in % of succinic acid, Ka value decreases as well as dissociation increases.

Table 1: Physical properties of Electrolyte solvents

Solvent	M.Wt	Melting Temp	Boiling Temp	Viscosity at 250 C	Dielectric constant at 250 C	Dipole Moment	Flash Temp	Density(gm/c.c.) at 250 C
PC	102	-48.8	242	2.53	64.92	4.81	132	1.200
THF	72	-109	66	0.46	7.4	1.7	-17	0.88

Table 2: Slope value of loglm vs logC of succinic acid with (Water +PC)

Slope	150C	250C	350C	450C	Water +PC
	-0.16	-0.28	-0.33	-0.28

 

Table 3: Slope value of loglm vs logC of succinic acid with (Water +THF)

Slope	150C	250C	350C	450C	Water +THF
	-0.23	-0.21	-0.25	-0.23

Table 4: Limiting molar conductance of  succinic acid solvated in (Water +PC) and (Water + THF) medium from 288K to 318K.

Serial no	Temp(in K)	1/T(K-1)	Water+ PC (lm0)	Water+ THF (lm0)
1.	288K	0.0034	370.87	384.61
2.	298K	0.0033	400.00	454.54
3.	308K	0.0032	\1333.33	1666.66
4.	318K	0.0031	1428.57	2000.00

 

Table 5: Dissociation constant, activation of solvation and different thermodynamic parameters of succinic acid solvated in (Water +PC)  medium from 288K to 318K.

Temp	Kc	∆G(cal/mole)	∆S(cal/mole)	∆H(cal/mole)	∆Es(Kcal/mole)	lm0
288K	4.71	-892.75	-12.30	-2651.4	10.54	370.87
298K	3.96	-820.35	-11.64			400.00
308K	13.09	-1583.21	-13.74			1333.33
318K	15.28	-1734.21	-13.79			1428.57

∆H, ∆G, ∆S, ∆Es

Table 6: Dissociation constant, activation of solvation and different thermodynamic parameters of succinic acid solvated in Water +PC  medium from 288K to 318K.

Temp	Kc	∆G(cal/mole)	∆S(cal/mole)	∆H(cal/mole)	∆Es(Kcal/mole)	lm0
288K	4.53	-870.20	-6.45	-989.7	12.57	384.61
298K	3.83	-800.35	-6.00			454.54
308K	5.24	-1020.43	-6.52			1666.66
318K	8.72	-1377.55	-7.44			2000.00

Table 7: Ka(Association constant) values of succinic acid solvated in (Water +PC)  medium from 288K to 318K.

Temp	10%	20%	40%	50%	60%	80%
	Ka	Ka	Ka	Ka	Ka	Ka
288K	0.56	0.70	1.20	1.28	1.40	0.93
298K	9.9	2.02	1.02	0.88	0.93	1.06
308K	0.17	0.31	0.53	0.44	0.43	0.31
318K	0.23	0.40	0.50	0.48	0.51	0.48

 

Table 8: Ka(Association constant) values of succinic acid solvated in (Water +THF)  medium from 288K to 318K.

Temp	10%	20%	40%	50%	60%	80%
	Ka	Ka	Ka	Ka	Ka	Ka
288K	0.61	0.80	1.41	0.970	0.978	0.70
298K	0.47	0.75	0.85	0.92	1.0	0.76
308K	0.56	0.60	0.89	0.92	0.90	0.65
318K	0.48	0.80	1.26	0.97	0.86	0.83

 

From Table 7 & 8 it has been found that at the same temperature, Ka value increases with increase in solvent proportions, but to some extent different in 40% to 60% in both (water+ PC) and (water +THF) systems. As temperature increases, Ka value decreases normally. But some sort of discrepancies observed due to the switchover of ion-pair to ion-solvation interaction or vice versa.

According to the Fuoss, the slope of the plot loglm vs logC is around -0.5, it is an indication of the presence of ion pairs in equilibrium.

From Table 2, succinic acid with (water +PC) , the slope was found to be > -0.5. So, it suggests that there was an ion-pair present in equilibrium.

From the Table 3, succinic acid with (water + THF) , the slope value was also found . -0.5. So here also observe ion-pair in equilibrium according to Fouss.

From Table 4, for both succinic acid with (water + PC) and (water + THF) , as temperature increases, limiting molar conductance value increases. As the viscosity of THF is much lower than PC, so l_m⁰ value increases with temperature.

For this ion-solvent interaction process, activation of salvation is much important. The relation between limiting conductance value and activation solvation energy is related by this equation   λ_m⁰ = A. e-∆Es/RT

Where A= pre exponential factor, ∆Es = activation salvation energy, R= Molar Gas constant, T= Temperature in K.

If we plot logl_m⁰ vs 1/T, we get the slope. From the slope value we can easily calculate the activation salvation energy.

From the Table 5 and Table 6 , show the value of ∆Es for succinic acid with (water + PC) and (water + THF) in different proportions.

∆Es=10.54 Kcals for succinic acid with (water + PC)< ∆Es=12.57 Kcals succinic acid with (water + THF). It indicate that the lower value of activation energy, higher the dissociation as well as higher possibility of ion-solvent interaction than ion-pair interaction.

From these two tables if we compare the dissociation constant value at different temperature for (water+PC) and (water+THF) medium, as temperature increases, Kc value increases. It is more increases for (water+PC) medium as dielectric constant is much more higher than THF medium.

The Gibbs energies of dissociation were calculated using the following equation

∆G = -RT ln Kc…………..(iii)

Where Kc= dissociation constant.

The enthalpy change (∆H) of this dissociation process was calculated from the plot logKc vs 1/T. From the slope we can easily evaluate the value of ∆H. From the value of ∆G and ∆H, we can easily calculate ∆S for these systems by the equation

∆G= ∆H-T∆S………………(iv)

Where ∆S= Entropy of solvation

Conductance value decreases with increase the percentage of PC as well as THF in water medium. This basic concept supports our result in our present experiment.

Thermodynamic parameters were calculated with the help of Kc. ∆H value is negative for both the salvation processes. So it tells that in this dissociation process is exothermic in nature.

∆G value is much higher for (water+PC) medium which an indication of much spontaneous than (water+THF) medium.

∆S value is much negative for (water+PC) medium which indicate that this process is not much disorder for this ion solvent interaction process. At lower temperature, ∆S value is lower negative value. So, at lower temperature, ion solvent interaction is much random.

Figure 1: Limiting conductance at 288K of succinic acid with (water + THF) Click here to View figure

Figure 2: Limiting conductance at 298K of succinic acid with (water + THF) Click here to View figure

Figure 3: Limiting conductance at 308K of succinic acid with (water + THF) Click here to View figure

Figure 4: Limiting conductance at 318K of succinic acid with (water + THF) Click here to View figure

Fig.1 to Fig.4 shows the plot of shows the plot 1/lm vs. lmC of Succinic acid with (water+THF) medium.

Figure 5: Limiting conductance at 288K of succinic acid with (water + PC) Click here to View figure

Figure 6: Limiting conductance at 298K of succinic acid with (water + PC) Click here to View figure

Figure 7: Limiting conductance at 288K of succinic acid with (water + PC) Click here to View figure

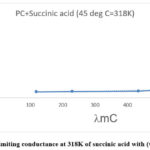Figure 8: Limiting conductance at 318K of succinic acid with (water + PC) Click here to View figure

Fig.5 to Fig.8 shows the plot of shows the plot 1/lm vs. lmC of Succinic acid with (water+PC) medium.

From these above plots we can evaluate l_m⁰ and Kc from the the slope and intercept respectively.

Figure 9: Plot of loglm at infinite dilution with 1/T of succinic acid with (water + THF) Click here to View figure

Figure 10: Plot of logKc with 1/T of succinic acid with (water + THF) Click here to View figure

Fig.9. shows loglm at infinite dilution with 1/T of succinic acid with (water + THF). From this graph we can evaluate the activation salvation energy with the help of slope.   Fig.10. shows the Plot of logKc with 1/T of succinic acid with (water + THF). From the slope we can calculate the ∆H for this system.

Figure 11: Plot of loglm at infinite dilution with 1/T of succinic acid with (water + PC) Click here to View figure

Figure 12: Plot of logKc with 1/T of succinic acid with (water + PC) Click here to View figure

Fig.11. shows the  Plot of loglm at infinite dilution with 1/T of succinic acid with (water + PC) . From this graph we can evaluate the activation salvation energy with the help of slope.  Fig.12. shows the Plot of logKc with 1/T of succinic acid with (water + PC). From the slope we can calculate the ∆H for this system.

Figure 13: Plot of loglm vs logC of succinic acid with (water + PC) at 288K Click here to View figure

Figure 14: Plot of loglm vs logC of succinic acid with (water + PC) at 298K Click here to View figure

Figure 15: Plot of loglm vs logC of succinic acid with (water + PC) at 308K Click here to View figure

Figure 16: Plot of loglm vs logC of succinic acid with (water + PC) at 318K Click here to View figure

Fig.13. to Fig.16 show the Plot of loglm vs logC of succinic acid with (water + PC) at 288K to 318K. From these plots we evaluate the slope. From the slope value we imagine that at equilibrium the systems are ion-pair interaction occurs or not.

Figure 17: Plot of loglm vs logC of succinic acid with (water + THF) at 288K Click here to View figure

Figure 18: Plot of loglm vs logC of succinic acid with (water + THF) at 298K Click here to View figure

Figure 19: Plot of loglm vs logC of succinic acid with (water + THF) at 308K Click here to View figure

Figure 20: Plot of loglm vs logC of succinic acid with (water + THF) at  318K Click here to View figure

From these 8 plots it has been found that both systems show ion-pair interaction in equilibrium processes according to Fuoss.

For the further studies in this way we can easily calculate the thermodynamic parameters in different solutions in different concentrations (where different types of interaction happened). So, solution chemistry reveals of different ideas in physical chemistry.

Conclusion

From the solavation study of succinic acid with (water+PC) and (water+THF) medium it has been found that with increase in temperature limiting molar conductace increases in both the systems. Degree of dissociation (Kc) increases in both PC and THF medium. But it has been noted that to some extent high for PC medium. This is due to the high dielectric constant value of this medium. In both cases ∆H value is negative. So, these ion-solvent interaction systems are exothermic in nature. ∆G value is much higher for (water+PC) medium which an indication of much spontaneous than (water+THF) medium.  ∆S value is much negative for (water+PC) medium which indicate that this process is not much disorder for this ion solvent interaction process. ∆Es=10.54 Kcals for succinic acid with (water + PC)< ∆Es=12.57 Kcals succinic acid with (water + THF). It indicate that the lower value of activation energy, higher the dissociation as well as higher possibility of ion-solvent interaction than ion-pair interaction.

Acknowledgement

The author is thankful to the Principal as well as Dept of Chemistry, A.K.P.C. Mahavidyalaya. My younger brother Mr. Sandip Hazra, Deputy General Manager, Tata Motors, Pune always helps me for this study.

Conflict of Interest

There is no conflict of interest.

Funding sources

There is no funding source.

References

1. Hazra, A. ;  IJSTR, 2013, 2(4), 99.
   CrossRef
2. Hazra, A.; IJSTR, 2014, 3(3), 326.
3. Hazra, A.; Malik, A.;  Pan, A.; 2020, ACJ, IX(IV), 4269-4285.
4.  Srinivas, N.; Manikyamba, P.; Rasayan J. Chem, 2008, 1(2) 342-348.
5. Marcus,  Y.; Ion Solvation (Wiley nInterscience, New York), 1985.
6. Mahalakshmi, S.;  Laxmi Narayaan,  K.;  J Electrochem Soc. India, 1988, 37, 83.
7. Victor Pitchai,  J. ;  Muhuri Prakash, K.; Das, B.; Hazra, K.; Dilip;  The Journal of Physical Chemistry B 1999, 103(50), 11227-11232.
   CrossRef
8. Alasdair,  M. ; Christie, C.; Vincent, A.; The Journal of Physical Chemistry, 1996, 100(11), 4618-4621.
   CrossRef
9. Orest. Popovych, Analytical Chemistry, 1996, 38(1), 1174-119.
10. George,  J.;  Janz, S.; Danyluk,S.;  Chemical reviews,  1960, 60(2), 209-234.
    CrossRef
11. Marcel,  G. Goemans, E.; Funk, T. J.;  Michael A Sedillo, M. A.; Bhelow, S. J.; Anderson,G. K.;  The Journal of Supercritical Fluids, 1997, 11(1-2), 61-72.
    CrossRef

---

This work is licensed under a Creative Commons Attribution 4.0 International License.