Overtone Frequencies of NO2 Using Lie Algebraic Model

Introduction

The subject of the vibrational spectra of molecules is an interesting and innovative work in molecular spectroscopy. Studying the vibrational spectra of small-sized molecules at the fundamental and higher overtones aids in a better understanding of their molecular structure and allows to compare in vivo experimental results. The advent of novel experimental techniques to compute vibrational frequencies (higher overtones) of molecules requires a robust theoretical method for their elucidation of molecular structure. This paper examines vibrational spectra of nitrogen dioxide in higher overtones using a theoretical approach – Lie algebraic model. In this model, Hamiltonian operator describes the vibrational energies of the molecule. In 1991, Iachello and co-researchers applied U(2) Lie algebraic approach for the analysis of ro-vibrational spectra of small size molecules ¹ and then this method was improved in subsequent works to study molecular spectra of polyatomic molecules ^2-10.

Lie algebraic model

Nitrogen dioxide is a bent molecule with C_2v point group symmetry.with symmetry species – A₁ (Symmetric Stretch), B₂ (Antisymmetric Stretch) and A₁ (Bend).

Figure 1: Structure of nitrogen dioxide. Click here to View figure

The general Hamiltonian for n vibrational modes (N-O and N-O)is

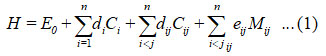
In the equation (1), C_i and C_ij are invariant operators of uncoupled and coupled bonds respectively and known as

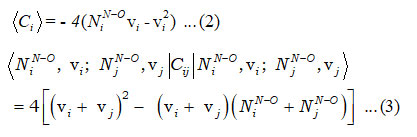
and the Majorana operator M_ij is used to express the local mode interactions in pairs and contains diagonal and non-diagonal matrix elements,

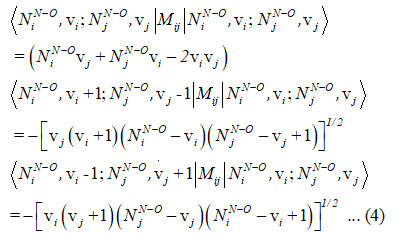
Hamiltonian for two stretching vibrationsof  nitrogen dioxidecan be written as

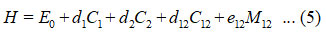
In equation (5), d₁, d₂, d₁₂ and e₁₂ are algebraic parameters (cm^-1), determined from available spectroscopic data. From the structure of nitrogen dioxide, two bonds (N-O) are equivalent; hence we consider as d₁= d₂,=d, N₁^N-o = N₂^N-o = N^N-o in equations (2), (3) and (4).Vibrational frequencies of the molecule can be determined from the Hamiltonian matrix.

For the first two local oscillators, the Hamiltonian matrix is

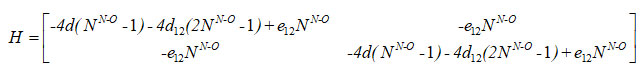
Results and Discussion

The energy equation (6) is used to detrmine the starting value of parameter d,

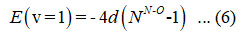
and the value for e₁₂ calculated from the relation,

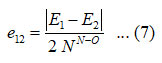
Where, E₁, E₂ are symmetric and antisymmetric vibrational frequencies of the molecule, respectively. The Lie algebraic method was used to calculate nitrogen dioxide vibrational frequencies, which are presented in table (2) and table (3).

The Vibron number N₁ (dimensionless) for stretching bonds of nitrogen dioxide using

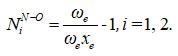
Where, u_e (= 1906.52), u_e x_e (= 14.504) are harmonic vibrational frequency and vibrational anharmonicity (spectroscopic) constants, respectively for the bond N-O ¹².

Table 1: Fitted algebraic parameters

NN-o (stretch)	130
No-N-o (bend)	72
d(stretch)	-2.7221
d(bend)	-2.5213
d12(stretch)	0.1447
d12(bend)	-0.0033
e12(stretch)	1.1538
e12(bend)	3.3641

 

Table 2: The fundamental vibrational frequencies (in cm^-1) of NO₂

Vibrational Mode	Experimental#	Lie algebraic method
A1 (Symmetric Stretch)	1318	1318.0976
B2(Antisymmetric Stretch)	1618	1618.0856
A1 (Bend)	750	751.656

 

Table 3: Vibrational frequencies (in cm^-1) of NO₂ in higher overtones (Lie algebraic method).

Overtone	Vibrational mode
	A1 (Symmetric Stretch)	B2 (Antisymmetric Stretch)	A1 (Bend)
I	2566.2043	3212.8301	1456.0532
II	3912.0712	4787.0381	2186.8400
III	5297.0095	6446.8082	2954.4269
IV	6575.9632	7975.3307	3687.4820
V	7893.7510	9679.4237	4476.7362
VI	9184.0196	10877.3129	5175.6613

 

Figure 2: Graphical representation of higher overtone vibrational frequencies Click here to View figure

Conclusion

In the table (2), the estimated vibrational frequencies in fundamental mode were compared with the experimental data available and in table (3), vibrational frequencies upto the fifth harmonic by Lie algebraic approach are reported. The calculated results can be helpful for experimentalists and theorists to extend the vibrational spectra of NO₂ in higher overtones.

References

1. F. Iachello, S. Oss, R. Lemus, J. Mol. Spectrosc., 1991, 149 (1), 132-151. doi: 10.1016/00222852(91)90148-4
   CrossRef
2. F. Iachello, S. Oss, J. Mol. Spectrosc.,  1992, 153 (1–2), 225-239. doi: 10.1016/0022- 2852(92)90471-Y
   CrossRef
3. A. Frank, R. Lemus, R. Bijker, F. Péilez Bernal, J.M. Arias, Ann. Physics, 1996, 252, 211-238.
   CrossRef
4. Zhaochi Feng, Guang Xiong, Qihua Yang, Qin Xin & Can Li, Chin Sci Bull, 1999, 44, 1961–1964. doi:10.1007/BF02887118
   CrossRef
5. F. Iachello, S. Oss, Chem. Phys. Lett., 1991, 187 (5), 500-505.
   CrossRef
6. F. Iachello, S. Oss, Chem. Phys. Lett., 1993, 205 (2-3), 285-289.
   CrossRef
7. M. R. Balla, V. S. Jaliparthi, Mol. Phys., 2021, 115 (5), e1828634.
   CrossRef
8. M. R. Balla, V. S. Jaliparthi, Polycyclic Aromatic Compounds , 2021.doi: 10.1080/10406638.2021.1901126.
   CrossRef
9. M. R. Balla, S. Venigalla, V. Jaliparthi,Acta Phys. Pol. A , 2021, 140 (2), 138-140. doi: 10.12693/APhysPolA.140.138
   CrossRef
10. V. Jaliparthi, M. Rao Balla, Spectrochim. Acta A, 2022, 264, 120289(1-8). doi:10.1016/j.saa.2021.120289
    CrossRef
11. J. Vijayasekhar, Orient J Chem, 2018, 34(4), 2208-2210. doi:10.13005/ojc/3404065
    CrossRef
12. Irikura, K.K. J. Phys. Chem. Ref. Data., 2007, 36(2), 389-398.
    CrossRef

---

This work is licensed under a Creative Commons Attribution 4.0 International License.