Lattice Dynamical Study and Elastic Property of Europium Telluride (Eute) Crystal

Introduction

The electronic structure of Europium telluride (EuTe), which is a family of Europium Chalcogenides crystallize in F. C. C. NaCl structure and are also called rare earth europium chalcogenides. Europium Telluride (EuTe) is a crystal grown product generally immediately available in most volumes. Unlike other rare earth compounds europium chalcogenides generally, show non-mixed valance character. Complete experimental data on phonon dispersion is available for EuTe, which has been reported. by Silberstein et al. ¹. Zeyher and Kress ² discuss the complete phon0n dispersion curves (PDC), combined density of states (CDS) ³ and Debye temperature variations curve given by ⁴. The parameters like elastic & dielectric constants ^{5, 6}, the physical-natural properties of the (EuTe) have been attracted and their explication through different conceptual models ^7-12, which has also satisfyingly narrated their engrossing properties. It has been establishing the interactions of three body which demonstrate the optical branches and Cauchy discrepancy concurrently to almost all the ionic-semiconducting crystals ¹³. The remarkable success achieved from (RIM) ¹⁴ and (RSM) ¹⁵ represent the lattice properties of alkali halides and worthwhile to explore the adequacies of these model for EuTe. The third-order elastic constants (TOEC), which is related to the energy products of three strain components, and the lowest order constants to enter the description of non-linear effects like the equation of state and the interaction of phonons. These TOEC is determined from velocity measurements on small amplitude sound waves in statically stressed media. The aim of present report is to test the applicability and utility of second-neighbor three-body rigid shell model (TRSM) and second neighbor three-body rigid ion model (TRIM) with the satisfactory description of phonon dispersion relations and other phonon properties of the EuTe.

Theory

The existing model accordingly consists of the comprehensive shield Coulomb, TBI and the sh0rt-range overrun repulsion effective up to the next-neighbor for EuTe. The relevant expression for the crystal potential per unit cell can be extrapolate TBFSM, is given as

where φ^C is comprehensive Coulomb reciprocity potential. where φ^R is a short-range repulsion & φ^TBI long-range TBI interaction potential by ¹⁶ . The secular determinant equation is given by

The dipole’s (VWI) efficient next- neighbor is given as:

By use of Eq. (2) the Eq. for elastic constants can give as:

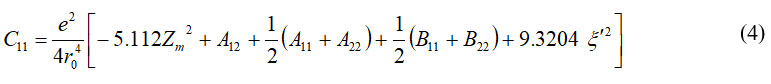
Vibrational Properties of EuTe

The term fo is based on 0verlap integrals of charge (e^–) wave functions and expressions for optical vibration frequencies (w_L and w_T) are given as:    

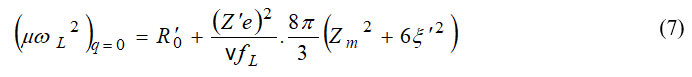
By using Debye’s model distribution function for frequency is given by

the density of states of phonon for each polarization is given by   

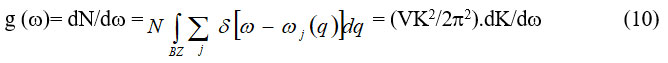
and N = (L/2 π)³ (4 πK³/3) and phonon wave vector q such that ∫ g (ω)d ω = 1

Table 1: Cauchy-Discrepancy (in units 10¹² dyne/cm²) for EuTe

Cauchy-Discrepancy
Property	Values for EuTe
C112– C166	-0.3501831
C123– C456	0.2610215
C144– C456	0.0870346
C123–C144	0.1739869
C1112– C1166	2.3062965
C1122– C1266	0.1261647
C1122– C4444	0.637605
C1123– C1144	-0.0232144
C1123– C1456	-0.1482605
C1123– C1244	-0.4385078
C1123– C4466	-0.4158073

Numerical Computations: The input data and calculated model parameters from SMTRSM and SNTRIM for EuTe are given in Table- 2.

Table 2: Input data, model parameters for EuTe in-C_ij (in 10¹² dyn/cm²), r_o(in 10^-8 cm).

Input data for EuTe		Model parameters for EuTe
Properties	Values for EuTe	Parameters	TRSM	TRIM
C11	9.36	r 0 f0′	-0.0262	-0.0262
C12	0.67	Zm2	0.5965	0.5722
C44	1.63	A	12.702	12.6113
ro	0.24	B	-0.6950	-0.6667
α1	8.76	d1	0.4136	———-
α2	3.292	d2	0.9680	———-
		Y1	-0.2382	—————
		Y2	-3.7420	——————-

 

Table 3: Combined Density States curve for EuTe

Raman Active -(Present study)
Frequency  In (THz)	Branch	Values (cm-1)
42	L0(X)-LA(Δ)	43
74	LO(X)–TA(X)	75
116	LA+TA(X)	118
157	LA(X)+TA(Δ)	158
172	2LA(Δ)	172
189	TO+LA(Δ)	189
206	2TO(∆)	205
234	2LO(X)	233
257	2LO(Δ)	255
287	2LO(┌)	286

 

Table 4: TOEC & FOEC (in units 10¹² dyne / Cm²), Pressure derivatives of SOEC and TOEC for EuTe

TOEC and FOEC (in units 1012 dyn / Cm2)		Pressure derivatives of SOEC and TOEC (dimensionless)
Property	EuTe (Present)	Property	EuTe (Present)
C111	2543.4513	dK′/dP	66.328857
C112	-1.9844249	dS′/dP	36.399633
C123	1.2280826	dC′44/dP	-2.7321557
C144	1.0540957	dC′111/dP	-4263.2546
C166	-1.6342418	dC′112/dP	-3.3262317
C456	0.9670611	dC′166/dP	2.7392656
C1111	3483.4014	dC′123/dP	2.0584741
C1112	8.0187951	dC′144/dP	-1.7668426
C1166	5.7124986	dC′456/dP	1.6209
C1122	8.0187951
C1266	7.3894107
C4444	7.9006065
C1123	-1.9385487
C1144	-1.9617631
C1244	-2.3770565
C1456	-2.0868092
C4466	-2.35435

 

Results

The present approach is effectively described the crystal dynamics of (EuTe), eight parameter’s with elastic constants (C₁₁, C₁₂ & C₄₄), six short range force constants parameters r₀ f₀¢, ionic charge z, shell charge Y, polarizabilities (α₁, α₂), & polarizability (mechanical) ‘d’ developed by ¹⁶ for (EuTe) are reported in Table-1 by using Eq.1 & 2.The knowledge of lattice vibration frequency (CDSc)  reports in table.2 by computing N (ν_{j +} ν’_j)of the combined frequencies(ν_{j +}ν’_j)_. The combined density data is reported in Table-3. The sensitivity of two-phonon Raman spectra is towards high-frequency side of the phonon spectra and specific heats towards its lower side is confirmed the validity of present model f0r its full wavelength range. The 3^rd & 4th order elastic constant and its pressure derivatives for (EuTe) are given in Table-4. Which is probably the first reports in the absence of experimental data, but their reliability test is not possible. The reported result by use of SNTRSM for (EuTe) is comparatively nearer to the measure data on PDCs, which are showing in the figure- 1(a), (b) and (c). These results for TMC and its some features 0f PDC for (EuTe) are specially reporting here. The interactions of three body have affected both LO & TO branches, more than acoustic branches (LA and TA). Other striking feature is excellent reproduction of optical and acoustic branch. The model parameter of TRSM & TRIM is used to calculate the frequency along with uniformity and curve is plotted between wave vectors versus obtain (PD) from this model. These curves are measure up with use of inelastic neutron scattering technique. The specific heat data has been enumerating at variable temperature by Blackmann’s ¹⁷ and the Debye temperature curve is plotted with absolute temperature (T). Qualitatively the TRSM model is prominent than some of the model values. In addition, some other researchers ^18-22 of the same field of research have also tried to report their best to explain PDCs and other properties of europium chalcogenides but only with moderate success. To increase the merit of this work we have calculated 33 two phonon IR/Raman spectra and alteration of Debye temperatures shown in figure 2. The (CDS) peaks is compare with theoretical data, shown in figure 3. The interpretation of critical point study has been used by Burstein et al. ²³     

Figure 1: Phonon Dispersion Curve for [EuTe] Click here to View figure

Figure 2: Debye temperature curve for [EuTe] Click here to View figure

Figure 3: Combined density of states curve for [EuTe] Click here to View figure

Conclusion         

Although, quantitively the agreement achieved from our present model TRSM is good. Furthermore, slight discrepancies still occurring between theory and experiment may be further improved by including the effect of free carrier screening (FCS), Van der Waals interactions (if data are available in future) and by including anharmonic vibrations in the present model (TRSM). A large group of researchers also have successfully reported theoretical results for some other alkali halides and semiconducting materials ^24-31 by use of the present model which shows the validity of this model.  

Acknowledgement

I pay my tribute to my supervisor Late Prof. Dr. K S Upadhyaya sir, for their guidance and continuous support in the preparation of this paper. I am also thankful to my respected principal Dr. Sangeeta Gupta, for her support and motivation.

Conflict of interest

Funding facility is not given by any agencies.

References

1. Silberstein, R.P.; Tekippe, V.T.; Dresselhaus, M.S, Physics Rev. 1977, B16,2728.
   CrossRef
2. Zeyher,R.;  Kress, W, Physics Rev. 1979,B20,2850.
   CrossRef
3. Smart,C.; Wilkinson,G.R.; Karo,A.M.; Hardy, J.R .;lattice Dynamics ,edited by R.F.Wallis (Pergamon Press ,Oxford),1965.
4. Blackmann,M.; Z. Phys. 1933,82, 421 ; Trans. Roy. Soc. 1955, A236, 102.
5. Wyckoff, R. W.G.; Crystal structure, (Wiley, New York), 1963.
6. Guntherod,G.; Physics Condensed Matter, 1974,18,37.
   CrossRef
7. Gupta,H.N.; Upadhyaya, R.S.; Physica Status Solidi,1980,B102, 143.
   CrossRef
8. Singh, R.K.; Gupta,H.N.; Proc. Royal Society London,1976,349, 289 .
   CrossRef
9. Mishra,V.; Sanyal ,S.P.;  Singh,R.K.; Phil. Mag,1981. A55, 583.
   CrossRef
10. Singh,R. K.; Gupta, H.N.; Sanyal, S.P.; IL Nuovo Cemento, 1980,60, 89.
    CrossRef
11. Lal, H.. H.; Verma, M .P.; Journal Phys. C, Solid State Physics, 1972,5, 543.
    CrossRef
12. Upadhyaya,.Kripa. S.; Yadav, M.; Upadhyaya,G.K.; Phys. Status Solidi, 2002,B229, 1129.
    CrossRef
13. Kellerman, E.W. ; Phil.Trans.Roy.Soc.(London), 1940,A 238,513.
    CrossRef
14. Woods, A. D. B. ; Cochran, W.; Brockhouse, B .N.; Physical Review,1960, 119, 980.
    CrossRef
15. Verma, M. P.; Singh,R.K.; Physica Status Solidi ,1969,33, 769.; 1969,36, 335 ; 1970,38,851 .
    CrossRef
16. Blackmann, M.; Phys Z. ,Trans. Roy. Soc,1955. A236,102.
17. Sanyal, S.P.; Singh, R.K.; Physica  B, 1985,132, 201.
    CrossRef
18. Mischenko, A.S.; Kikoin ,K.A.; J. Phys. Codens. Matter ,1991,3, 5937.
    CrossRef
19. Jha, P.K.; Sanyal, S.P.; Indian J.Pure and Applied. Physics, 1993,31,469.
20. Jha, K.; Sanyal, S.P.; Indian Journal of Pure and Applied Physics, 1994,32,:824-829.
21. Jha, P.K.; Sanyal, S.P.; Pramana, Solid State Communication, 1998,105,455.
    CrossRef
22. Burstein, E.; Jhonson, F.A.; Landon ,R.; Phy. Rev. 1965,139 A, 1239.
    CrossRef
23. Sakake, U.K.; Jha, P.K.; Sanyal, S.P.; Bull. Mat. Science.,2000, 23,333.
    CrossRef
24. Singh, S.P, Thesis Ph.D, Three body Interaction of lattice dynamics of Europium chalcogenides (V B S Purvanchal University, Jaunpur), 2005.
25. Srivastava, U.C.; Upadhyaya, Kripa .S.; Rapid Communication (OAM – RC), 2010,V 4,  9, 1336.
26. Srivastava. U.C.; Optoelectronics and Advanced Materials, Rapid Communications (OAM-RC), 2013, Vl7,9-10, 698-701.
27. Srivastava, U.C.; International Journal of Modern Physics B, 2016,30, 1750020-28.
28. Srivastava, U.C. ; Journal of Science and Arts, 2017, 2(39 ), 309-320.
29. Singh,S.P.; Srivastava, U.C.; Upadhyaya, K. S.; International Journal of Scientific & Technology Research (IJSTR), 2021,V9,4, 472-478. 
30. Srivastava, U.C.; Johnson Matthey Technol. Rev., 2021,65,1, 87-93.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.