Vibrational Frequencies of Dichlorine Monoxide: A Mathematical Model

Introduction

Calculation of fundamental and higher overtones of molecule useful to understand molecular structure. We applied Lie algebraic method to calculate vibrational frequencies (wavenumbers) of molecule.This mathematical approach helps to calculate vibrational frequencies in higher overtones and moreover useful to compare in-vivo experimental results. The vibrational wavenumbers of the molecule are analyzedby means of traditional approaches, Dunham series expansion and Potential function approach. The noticabledemerit of these approaches are, requirement of huge experimental data to fit the parameters. We choose this method,as it overcomes this difficulty. In this method, vibrational frequencies are calculated using Hamiltonian operator[1-6].

Lie Algebraic Method for Cl₂O

Dichlorine Monoxide (Cl₂O) contains two chlorine (Cl) atoms and one oxygen atom with two Cl – O bonds. Symmetry point group is C_2v with symmetry species A₁ (Cl – O symmetric stretching), .B₂ (Cl – O asymmetric stretching) and A₁ (Cl-O-Cl bending). This framework explains the stretching bonds in Cl₂O molecule using two Lie algebras i.e.( U₁(2) and U₂(2))

Below mentioned two chains, explains the molecular dynamical group.

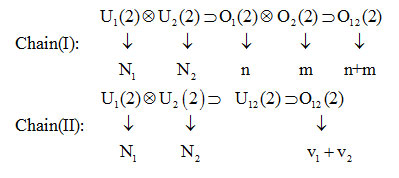
chain (I) represents the local and chain (II) represents the normal couplings. Quantum numbers in the chain (I) related to algebras, indicated by n, mand in the chain (II) are v₁ , v₂. Vibron numbers N₁ and N₂ are taken to be constants and are related to the maximum number of bound states of two Morse oscillators. Bending vibrations can be represented with the algebra   U₃(2) and combined with the algebra U₁(2) U₂(2) associates with the coupled stretching vibrations.Hamiltonian operator  [9,10]  

( stretching vibrations) of this molecule :

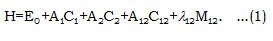
In equation (1), A₁, A₂, A₁₂ and λ₁₂ are the algebraic parameters, which are calculated from experimental spectra. The local stretching vibrations are denoted by (v₁) and (v₃), where as (v₂) representing bending vibrations for Cl₂O. The Hamiltonian in the equation (1) can be diagonalized to get vibrational frequencies. Where in the equation (1), C₁, C₂ are invariant operators of the uncoupled bonds with eigenvalues -4 (N_i v_i – v_i² )(i =1,2) and C_ij (i =1,2) operator for coupled bonds is diagonal with matrix elements 

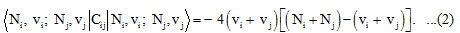
The Majorana operator M_ij ( i =1,2)in the equation (1), describes local mode interactions in pairs and provide diagonal and non-diagonal matrix elements

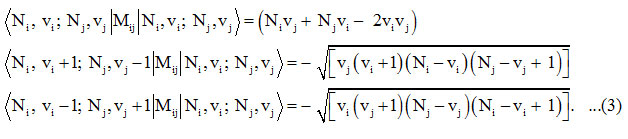
The Hamiltonian matrix for the local modes is given by  

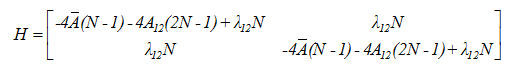
Results and Discussion

The parameters for stretching bonds of the water molecule in equations (1), (2) and (3) as N_{i =} N, A_i = A, A_ij = A₁₂, λ_ij = λ₁₂ ( i =1,2). The vibron number N_i ( i =1,2).  calculated from the relation [9]

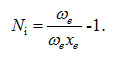
Here ω_e and ω_ex_e are the spectroscopic constants [11]. The value of the parameter  is obtained by using the energy equation [9,10] for the single-oscillator fundamental mode, which can be calculated from

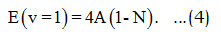
Using the equation (4), Ā can be evaluated as,

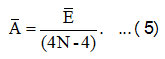
In equation (5), Ā and Ē are the average values of the algebraic parameters A’s and E’s. Theinitial value of λ₁₂ , estimate by the relation [10],

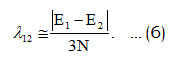
In order to calculate accurate results, a numerical regression fitting method is used to fit the algebraic parameters A, λ₁₂  starting from the values as given by equations (5) and (6). The initial value of A₁₂ assumming as zero.

Table 1: Stretching vibrational frequencies (in cm^-1) of Cl₂O                

vib. quantum no.	observed [11]	calculated
(1 0 0)	639	638.274
(0 0 1)	686	686.932
(2 0 0)	–	1245.407
(0 0 2)	–	1357.652
(3 0 0)	–	1911.094
(0 0 3)	–	2043.086
(4 0 0)	–	2537.335
(0 0 4)	–	2687.320
N= 154, A= -1.9091, A12 = 0.9328,=0.1863

Conclusion

Stretching vibrational frequencies of Cl₂O upto third overtone are calculated and compared with  experimental data in fundamental mode.Vibrational frequencies (stretching) of Cl₂O are in close agreement with experimental values in fundamental mode.

References

1. Iachello, F.Chem. Phys. Lett. 1981, 78(3),581-585.
   CrossRef
2. Iachello, F. ; Levine, R. D. J. Chem. Phys. 1982, 77, 3046-3055.
   CrossRef
3. Frank, A.; Iachello, F.; Lemus, R.Chem. Phys. Lett.1986, 131(4-5), 380-383.
   CrossRef
4. Karumuri, S. R.; Vijayasekhar, J.;Sreeram, V.; Uma Maheswara Rao, V.; Basaveswara Rao, M. V. J. Mol. Spectrosc. 2011, 269, 119-123.
   CrossRef
5. Karumuri, S. R.;Srinivas, G.;Vijayasekhar, J.; Rao, V. U. M.;Srinivas, Y.; Sunil Babu, K.; Kumar, V. S. S.;Hanumaiah, A.Chin. Phy. B. 2013, 22(9), 090304(1-8).
   CrossRef
6. Karumuri, S.R.; Sravani, K.G.; Vijayasekhar, J.; Reddy, L.S.S.  Acta Phys. Pol. A. 2012, 122 (1), 49 52.
   CrossRef
7. Balla, M.R.; Jaliparthi, V.S. Mol. Phys. 2020. DOI: 10.1080/00268976.2020.1828634
   CrossRef
8. Frank, A.; Lemus, R.; Bijker, R.Ann. Phys.1996, 252,211-238.
   CrossRef
9. Iachello, F.; Oss, S. J. Mol. Spectrosc. 1990, 142(1), 85-107.
   CrossRef
10. FENG, Zhaochi.; XIONG, Guang.; YANG, Qihua.; XIN, Qin.; LI, Can.Chin. Sci. Bull. 1999, 44(21), 1961-1964.
    CrossRef
11. Irikura, K.K. J. Phys. Chem. Ref. Data.2007, 36 (2), 389-398.
    CrossRef
12. Shimanouchi, T. Tables of Molecular Vibrational Frequencies Consolidated Volume I, National Bureau of Standards, 1972, 1-160.
    CrossRef

---

This work is licensed under a Creative Commons Attribution 4.0 International License.