The structure of qubit and quantum gates in quantum computers
Yadollah Farahmand 1,3*,Zabialah Heidarnezhad 2, Fatemeh Heidarnezhad 2 , Kh. Kh. Muminov 1 ,Fatemeh Heydari2 and Ghasem Saidi Tabar4
1Physical-Technical Institute named after S.S.Umarov Academy of Sciences ,Dushanbe, Tajikistan 2Department of Chemistry, Andimeshk Branch, Islamic Azad University, Andimeshk , Iran 3Farhangiyan Golestan University,Iran 4Department of Chemistry ,University of Lorestan,Khorramabad.Iran
DOI : http://dx.doi.org/10.13005/ojc/300438
Article Received on :
Article Accepted on :
Article Published : 01 Jan 2015
In regard to the important of qubits role and quantum gate in quantum computers, in this article we will consider to the qubit structure and quantum gate on the basis of theory and quantum principles and in various from we will show the qubit and quantum gate (quantum operator). Finally we will express cloning theorem the quantum computers by binary gate.
KEYWORDS:quantum theory; quantum computer; qubit; quantum gate; quantum operator; cloning theorem
Download this article as:| Copy the following to cite this article: Farahmand Y, Heidarnezhad Z, Heidarnezhad F, Muminov KH. KH, Heydari F, Tabar G. S. The structure of qubit and quantum gates in quantum computers. Orient J Chem 2014;30(4). |
| Copy the following to cite this URL: Farahmand Y, Heidarnezhad Z, Heidarnezhad F, Muminov KH. KH, Heydari F, Tabar G. S. The structure of qubit and quantum gates in quantum computers. Available from: http://www.orientjchem.org/?p=6537 |
Introduction
The quantum computers in the case of practical realization can outreach from the best modern computers, in quantum world there are phenomena in a different and amazing kink and so using them in making quantum computers for the process of information is suitable . Engineers that design the quantum computers and the experts of mechanic quantum hope that use from one of the most basic quantum theories principles for design of system (machines) that are able to do parallel computation concurrently, this computations provide the possibility of easy and logical solution of some of the problem that are insoluble in classical computers and also this computations provide the extant difficulty in ground of cry photography.
The memory of a quantum computer is quantum states, quantum computers are mode from qubit .qubit can have zero bit and one bit concurrently i.e. they are equality with superposition of classical bits. So quantum states can be consider as quantum computer bits .in regard to that quantum states are mode from phenomena of quantum mechanics ,so computation of quantum computers are found on the base of physics process and quantum principles.
Qubit is the smallest part of a system (memory unit) in quantum computers that is analog bit in classical computers. Each quantum state that is superposition of
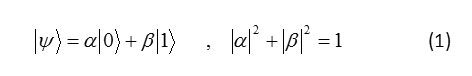
In regard to the condition of norm there are number of infinity amounts for ,and infinity concurrently state for qubit . The main works of quantum computers are in a way that processes concurrently the qubits that are include infinity state.
In the base on basic principles of quantum mechanics theory , a qubit can has zero state and one state concurrently , so it is possible that a qubit take a part in more them one computation instantly , because of this the quantum computers are able to do a lot of parallel computation.
Bolch sphere representation
Bolch used from a sphere with unit rudius that are shown the angle points on sphere .opposite figure and the following connection are know as bolch sphere representation.
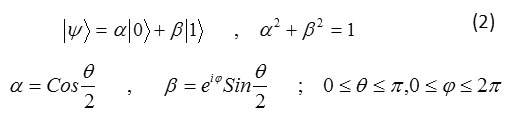
 |
Figure 1 Click here to View figure |
Qubits representation to the form of matrix
Also qubits can be expressed to the form of matrix. 1, 2
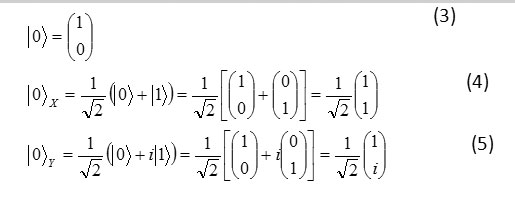
If two qubit place beside each other , i.e. correlation between the first and the second qubit come into existence , with application of tensor multiplication between them it’d matrix representation will be obtained
Binary qubits
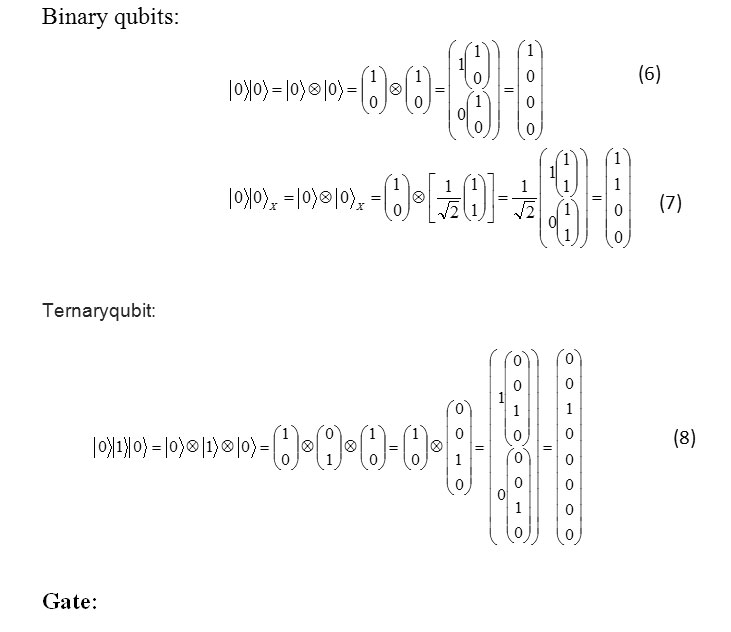
Process or bit transmission or qubit are shown by gate.
Classical gates
The first discussion of the classical computers (classical computation) is the process or classical bit conversion. The only main elements of this classical process of bits are gates. A processor of new electronic computer includes hundreds and millions of gate, and each gate do the process proper to itself.
Quantum gate
The quantum gates are convertor of quantum bits , similar to classical gate that change the classical bits , with this difference that the quantum gate always are reversible 3
Dynamics
.Time and place evolution (transmission, rotation) in quantum system are described according to the laws of quantum mechanics by unitary operators
Unitary operator of rotation of circumaxis z
Tilver extension of function of multivariable can be expressed to the following form

Approximation of the first step of function of system state in tilver collar is to the following form
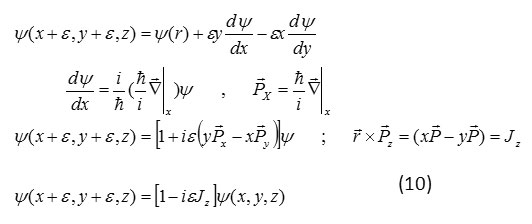
Besides , approximation of the first step of tilver extension of this unitary operator is to the following from
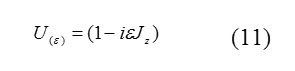
In Hyzenberg figure it can be said
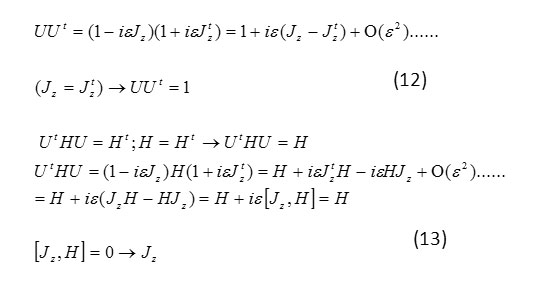
So Jz is fixed moving .rotation to the size of and can be mode from n infinitely small rotation consecutive U(ε) . That in here
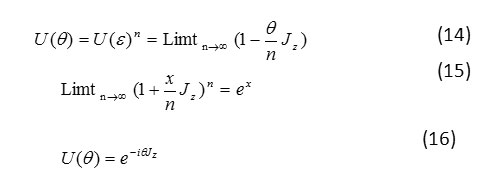
Generators of rotation group in the lowest dimension Jz=1/2

And in Total group we have

Unitary operator of time evolution
The time evolution of quantum state , is a unitary that is created by operator of self .adjoint H that is named system hamiltony . tilver extension of function Ψ (r,t + dt) with approximation of the first step for the time of infinitely small we have :
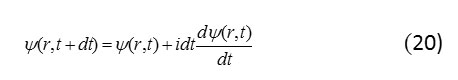
In regard to shruding are equation
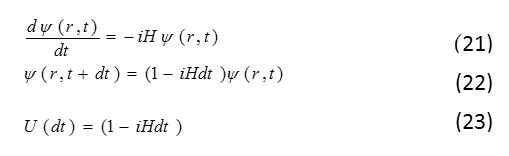
Because H operator is a hermit operator.
UUt = 24
While H is not connected to the time obviously and the time evolution U in finite times t we have:

So each quantum gate has a unitary operator since unitary evolution is a reversible evolution the quantum gate always are reversible.
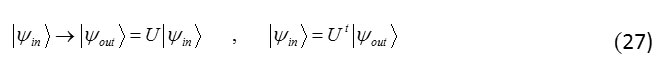
U is unitary operator i.e. don’t change the mass and length of the state : so the linear operator and U unitary is described as a quantum gate that can be applied on the main basis of single qubit |0>and |1>.
Contrary to the unitary evolution , the measurement process is caused to collapse from one state to another state (the main basis state) i.e. quantum system interaction to the measurement set , we an say that the measurement process is not a reversible process.
In follow we show the single quantum gates and binary quantum gates.
Single quantum gates
formula
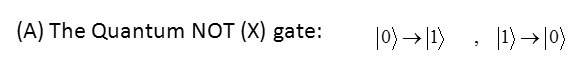
i.e. we define the following unitary matrix for that.
Example:
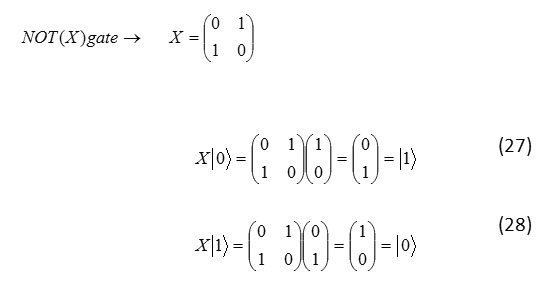
The model of physical gate not (X)
on the base of idea of atom state , qubits with apply a gate (photon absorption or photon emission with a energy equal to difference of ground state or exited state) the model of physical gateNOT(X) is shown to the following form 6.
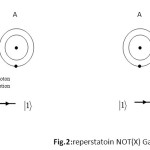 |
Fig2: reperstatoin NOT(X) Gate Click here to View figure |
Gate Y is similar to NOT(X) and this shown with the following matrix :
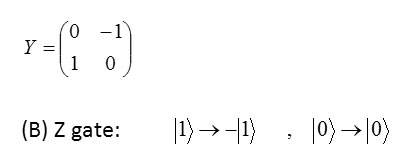
Matrix according to that is to the following from
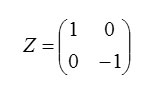
(A) Hadamard (H) gate:
A computation basic by gate hadmard operator is to the following from:
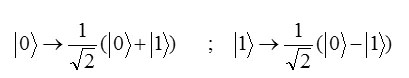
Correspondent matrix to that
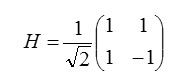
Usually the symbol of gate hadmard is to the following from:
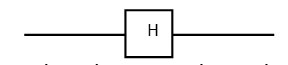
Gate Z and H don’t have any classical similarity
The model of physical gates Z and H :
The model of physical gates Z and H in spin quantum states an be seen in Stern – Gerlach experiments 7,8.
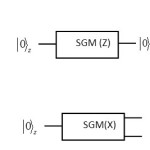 |
Figure 3 Click here to View fiugre |
The Controlled NOT (C-NOT) gate:
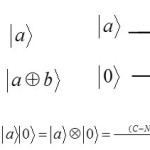 |
Figure 4 Click here to View figure |
The models of gate operation C-NOT on or the normal states:
Copy operation by gate C-NOT on the following orthonormal states is seen.
 |
Figure 5 Click here to View figure |
Gate operation C-NOT in other models
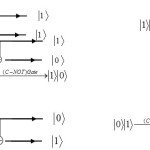 |
Figure 6 Click here to View figure |
(C-NOT) gate is one of the most importance quantum gate.
However this design and the primer plan are shown on the basis of physical principles , but the way of doing that is so difficult. In 1994 some men like zoller and cirac from Innsbruck University came in to view with a proposal model. They considered a net which is keeping a number of ions directly. This ions are cold by laser, and then each of them selectively are provoke by faint light of laser specially consequently this net will act
As a quantum cooler with a quantum state of each of ions that play the role of qubit. This light radiations can be caused to ions vibrations will have partnership by all existent ions in considered net, and are able to transmission of quantum information between ions distances and also is an instrument for quantum logical gates. In the middle of 1995 scientists of the national institute of standards and technology used from zoller and cirac idea for the purpose of making the first quantum gate that was started on two qubit9.
The Cloning theory 10
Coping for the or thonormal ground states is possible not for any ideal quantum state
Cloning theory is not to this mean that never can copy the qubits like
|Ψ> = α|> +β |1> but if exist the orthonormal state for that , this state can be copy by Cloning theory. For example
 |
Figure 7 Click here to View figure |
Conclusion
By using from theory and quantum mechanics principles we expressed the qubits that achieved from quantum states and from phenomenas of quantum mechanics by Bloch sphere or to the matrix from, so we can found the main structure of quantum computers and computation of quantum computers are founded on the base of physical process and quantum principles .qubit that are the smallest part of system (memory unit ) in quantum computers are like bit in classic call computers and we showed the models by physical phenomenas and quantum mechanics principles . so instructor of quantum computers, it can be said that the quantum gate are the converter of qubits that the same unitary operator are described according to quantum mechanics laws . in regard to this the quantum gates are always reversible and time evolution in quantum gates are visible . In this article we can find the express of Cloning theory and the main differences between classical computer and quantum computers.
References
- D.Mermin.2005.Lecture notes on Quantum Computation: I. Fundamental properties of cbits and qubits. Physics 481-681, CS 483.
- A.Chatterjee.2003. Introduction to quantum computation.quant-ph/0312111
- A. Ekert, P. Hayden, and H.Inamori.2001.Basic concepts in quantum computation.quant-ph/0011013.
- J.Perskill.2001.Lecture notes for Ph219/CS219: Chapter 2, Foundations I: State and Ensembles.
- G. Auletta. 2001. Foundations and Interpretation of quantum mechanics. World scientific, Singapore. New Jersey. London. Hong Kong, PP.47-49.
- G. Auletta. 2001. Foundations and Interpretation of quantum mechanics. World scientific, Singapore. New Jersey. London. Hong Kong, PP.759-781.
- G. Auletta. 2001. Foundations and Interpretation of quantum mechanics. World scientific, Singapore. New Jersey. London. Hong Kong, PP.531-544.
- J.J. Sakurai. 1982. Modern Quantum Mechanics.
- A. Ekert.2004. Introduction and over view.
- J.Perskill.2001.Lecture notes for Ph219/CS219: Chapter 4, Quantum Information and computation.

This work is licensed under a Creative Commons Attribution 4.0 International License.









