Validation and Verification the Expanded Table for Transition Metal Carbonyl and Main Group Element Cluster Series which obey the 18-Electron and 8-Electron (octet) Rules respectively
Enos Masheija Kiremire
DOI : http://dx.doi.org/10.13005/ojc/300404
Article Received on :
Article Accepted on :
Article Published : 30 Dec 2014
The transition metal carbonyl clusters and Main group element clusters belong to natural series based on the number theory. The number series of the cluster series have been generated using the empirical formula k = ½ (E-V) where k represents the linkages or bonds that glue together the cluster elements which obey the eighteen electron rule or the octet rule and E is related to the sum of eighteen electrons or the eight electrons and V is the sum of the valence electrons. An expanded cluster table been constructed to accommodate the analysis of medium to relatively large clusters of high nuclearity. Using the knowledge of k-value and the cluster table it is possible for a given cluster formula to be categorized into its type of series and its geometry deduced. This is relatively easy for simple to medium clusters. It is hoped that this simple approach to be adapted to categorize and deduce structures of clusters with high nuclearity. This approach to clusters using number theory will complement the existing clusters theories such as Wade-Mingos rules1-7, Jemmismno rules8-9 and topology rules10.
KEYWORDS:Transition Metal Carbonyl;18-Electron;8-Electron
Download this article as:| Copy the following to cite this article: Kiremire E. M. Validation and Verification the Expanded Table for Transition Metal Carbonyl and Main Group Element Cluster Series Which Obey The 18-Electron And 8-Electron (Octet) Rules Respectively. Orient J Chem 2014;30(4). |
| Copy the following to cite this URL: Kiremire E. M. Validation and Verification the Expanded Table for Transition Metal Carbonyl and Main Group Element Cluster Series Which Obey The 18-Electron And 8-Electron (Octet) Rules Respectively. Available from: http://www.orientjchem.org/?p=6246 |
Introduction
In our previous work, it was shown that in molecular systems in which the ‘skeletal atoms’ obey either the octet or the 18-electron rule, their bonds or linkages and shapes or symmetries are related to their k-values11-12, The k value is given by k = ½ (E-V) where E- is a parameter that is associated with either the octet electrons or the 18-electrons of the atoms and k to the number of bonds or linkages that act as a glue to link up the skeletal atoms in the molecule or cluster.By studying and analyzing the k-values of the known cluster series such as closo, nido, arachno and hypho, it is discovered that these are anly a tiny subset of an infinite number of cluster series. A smaller versions table of carbonyl cluster series and a corresponding one for main group elements were developed13. What is so fascinating is that the k-value is so precise. For instance, the k-values for N2, CO, O2, and F2 are 3, 3, 2 and 1 respectively. Surprisingly, the k vale for the diatomic species C2, CN+, BN, and CB― are each 4 in agreement with the recent high level theoretical calculations14. Even for complex cluster ions such as As113―and As224― the number of bonds to link up the cluster ion atoms are 15 and 31 respectively according to the empirical formula prediction and this wasobserved15.
Results and Discussions
The extensively expanded transition metal carbonyl clusters table has been created. It is given in Table 1. The same table can be utilized for the categorization of a given transition metal carbonyl cluster that obeys the 18-electron rule. The table can deduce the type of cluster the complex is such as closo or nido, or arachno or any other type belonging to one of the many cluster series and so on. It is also equally applicable to the categorization of main group element clusters by minor adjustment of the electron cluster valencenumber.
Categorization of a Cluster Formula
Categorizing the type of cluster series from the molecular formula can readily be done by calculating the k-value of the cluster. Let us take a few examples for illustration.
Fe2(CO)916;E= 2×18 = 36, V = 8×2+ 9×2 = 34, k = ½ (E-V) = ½ (36-34) = 1; code is M-2-1-34. Having obtained the code M-2-1-34, then the series table is scanned to see where it is located. As can be discerned the code is given a label of the type M-x-y-z where M = the skeletal atom, x = the number of the skeletal atoms, y = the k-value, z= the total number of valence electrons. The diagonal movement along the M-x will lead to the position where M-2-1-34 in this case is located. It is found that M-2-1-34 belongs to the A (arachno) series. The categorization code of the cluster is then M-2-1-34-A.A selected number of carbonyl clusters categorized in this manner are given in Table2. Furthermore, the two metal atoms are linear joined by one chemical bond. It may be compared to a simple main group compound such as BeF2 which is linear with a central atom. However, in case of M-2 cluster, there is no central atom. Nonetheless the structure is similar.
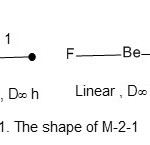 |
Figure 1 Click here to View figure |
Os3(CO)1216; E = 3×18 = 54, V = 8×3 +12×2= 48, k = ½ (E-V) = ½ (54-48) = 3; M-3-3-48 → M-3-3-48-o A. Hence the cluster, Os3(CO)12 belongs to the arachno series. The shape of the cluster is a trigonal planar. A similar compound from the main group elements is BF3. The shape is shown in Fig. 2.
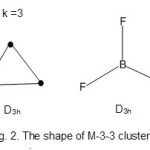 |
Figure 2 Click here to View figure |
Fe4(CO)132-;E = 4×18 = 72, V =8×4+13×2+ 2 = 60, k = ½ (72-60) = 6, M -4-6-60→N. Thus, the cluster16, Fe4(CO)132- belongs to the Nido (N )series. The ideal shape of M-4-6-60 clusters is tetrahedral Td. The structure is shown in Fig. 3. The Fe atoms occupy the positions similar to those of H atoms in methane. It can be viewed as a tetrahedral structure without a central atom.
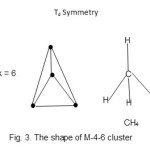 |
Figure 3 Click here to View figure |
Fe4(C)(CO)13;E = 4 x18 = 72, V = 4×8+ 4+13×2 = 62, k1 = ½ (E-V) = ½ (72-62) = 5. The cluster16 then becomes M-4-5-62- A. However, when the C atom is considered as part of the skeletal cluster atoms then E = 4×18+ 1×8 = 80 since the C atom has to obey the octet rule. In this way, k2 = ½ (80-62) = 9. The difference between the main group element and transition metal is 10 electron for one element. In order to use the transition metal cluster table when the C atom is included, we must add 10 to the valence electrons since we have only one C- atom. In this way the C atom is elevated to the metal atom and the cluster then becomes M-5-9-72. This is a closo system (C). The shape assumes a trigonalbipyramid geometry. This is summed up in Fig. 4. The cluster assumes a shape similar to that of SF4 and the C-atom behaves as a lone pair. Again in the case of the cluster, there is no central atom.
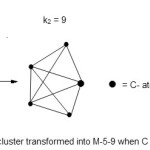 |
Figure 4 Click here to View figure |
Os5(CO)16E = 5x 18 = 90, V = 5×8+16×2 =72, k = ½ (90-72) = 9; code M-5-9-72 and from the cluster table, this belongs to the closo series.Hence, the cluster category is M-5-9-72-C. The shape of the cluster is trigonal bipyramid16. In this regard, it is similar to a trigonalbipyramid molecule such as PF5 but without a central atom. This shape is shown in Fig. 5.
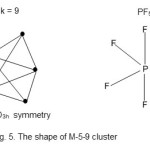 |
Figure 5 Click here to View figure |
There are other two more shapes encountered in the M-5 cluster series. These are the M-5-7-76-A and M-5-8-74-N. The ideal shapes are shown in Figs. 6 and 7.
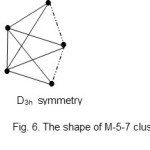 |
Figure 6 Click here to View figure |
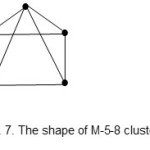 |
Figure 7 Click here to View figure |
The shape shown in Fig. 6 (M-5-7) is usually mistaken for a regular trigonalbipyramid (M-5-9).
A good example of M-5-8 cluster17 is Fe5(C)(CO)15. In this case, E = 90, E = 90, V = 74, k1 = 8. This gives rise to a square pyramid. When the C atom is taken into account, k2 = 12. This means C introduces 4 more additional linkages or bonds. This means the cluster assumes almost an octahedral geometry or a distorted one.
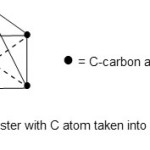 |
Figure 8 Click here to View figure |
The Fe5(C)(CO)15 cluster taking up aquare pyramid with a C atom present, it behaves in the same way as the a square pyramid molecule such as BrF5 , The position of the C atom corresponds to that of the lone pair in BrF5.
The octahedral geometry (Oh),M-6-11-86-C.
Os6(CO)182-; E = 108, V = 86, k = 11. This is the well knownoctahedral shape. The code and classification is M-6-11-86-C. This is a member of the closo series. Its shape is shown in Fig. 9.
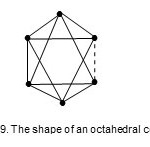 |
Figure 9 Click here to View figure |
Capping process in Clusters
Very good examples to illustrate the vertical movement (including capping) and horizontal movement within the same series have been derived from the paper derived from the paper by Hughes and Wade18. This can be viewed as a process of a vertical movement in the table as presented. In this way, the value of k changes by three units with an increase in nuclearity of the cluster by one each time.This concept can be well illustrated in the schemes below. The process involves the movement through different series. In this example, the start was with Arachno series, through Nido series and then Closo series and finally ended at mono cap series. For each shift there the k value changed by 3 units.
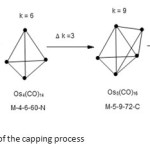 |
Scheme1: An example of the capping process Click here to View scheme |
As can be discerned, the movement involves adding an atom and 3 linkages at every step. Thus, from a triangle to a tetrahedral and then to a trigonalbipyramid geometry and so on. In this particular illustration, it is like capping at every step. In this connection, a trigonalbipyramid can be viewed as a capped tetrahedral while the shape of Os6(CO)18 the structure is a double capped tetrahedral.
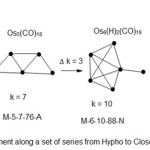 |
Scheme 2 Click here to View scheme |
In this particular scheme, the vertical movement involves addition of an extra atom and 3 linkages in such way that they distribute themselves to give final suitable symmetry.
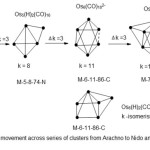 |
Scheme 3 Click here to View scheme |
The interesting feature in scheme 3 is the possibility of the cluster series M-6-11-86-C being able to have another geometry apart from the common octahedral (Oh) and generate another symmetry which a combination of a square pyramid and a monocap. In both cases k =11. We could regard this as a form of ‘k-isomerism’. It appears that the presence of hydrogen atoms tend to induce the k-isomerism. Let us take one more example to illustrate the vertical movement along the cluster series.
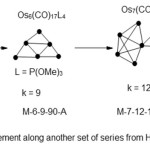 |
Scheme 4 Click here to View scheme |
Every step in vertical movement involves an atom accompanied by three linkages. However in terms of electron content, the change is only 12 in this case equivalent to the addition of Os(CO)2 fragment.
Horizontal Movement Along a Series
We have considered several illustrations of the vertical movement along various selected series. It was noted that such movement involves the change in k value by 3 units. In the case of horizontal movement along the series, the change in value is 2 and we remain in the same type of series. The final scheme 5 shows an example of horizontal movement along selected members of Arachno series
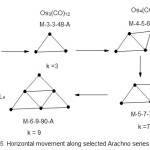 |
Scheme 5 Click here to View scheme |
The horizontal movement illustrated above is within the selected members of the Arachno series. Although the change in k value is 2 units, the electron count change is 14 corresponding an equivalent of Os(CO)3 fragment.
 |
Table1: An Expanded Table of Transition Metal Carbonyl Clusters Click here to View table |
Table 2: Selected Transition Metal Carbonyl Clusters for categorization
| COMPLEX | E | V | k | POSSIBLE CATEGORY | |
| Fe2(CO)9 | 36 | 34 | 1 | M-2-1-34-A | |
| Ru2(CO)9 | 36 | 34 | 1 | M-2-1-34-A | |
| Os2(CO)9 | 36 | 34 | 1 | M-2-1-34-A | |
| Fe3(CO)12 | 54 | 48 | 3 | M-3-3-48-A | |
| Ru3(CO)12 | 54 | 48 | 3 | M-3-3-48-A | |
| Os3(CO)12 | 54 | 48 | 3 | M-3-3-48-A | |
| Fe4(N)(CO)12– | 72 | 62 | 5 | M-4-5-62-A | |
| Fe4(CO)132- | 72 | 60 | 6 | M-4-6-60-N | |
| Fe4(CO)4(η5-C5H5)4 | 72 | 60 | 6 | M-4-6-60-N | |
| HFe4(C)(CO)12– | 72 | 62 | 5 | M-4-5-62-A | |
| Fe4(C)(CO)13 | 72 | 62 | 5 | M-4-5-62-A | |
| HRu4(C)(CO)12– | 72 | 62 | 5 | M-4-5-62-A | |
| H4Ru4(CO)12 | 72 | 60 | 6 | M-4-6-60-N | |
| HOs4(C)(CO)12– | 72 | 62 | 5 | M-4-5-62-A | |
| Os4(CO)16 | 72 | 64 | 4 | M-4-4-64-H | |
| Os4(CO)14 | 72 | 60 | 6 | M-4-6-60-N | |
| Fe5(C)(CO)15 | 90 | 74 | 8 | M-5-8-74-N | |
| RuIr4(CO)152- | 90 | 76 | 7 | M-5-7-76-A | |
| Ru5(C)(CO)15 | 90 | 74 | 8 | M-5-8-74-N | |
| H2Ru5(CO)16 | 90 | 72 | 8 | M-5-9-72-C | |
| H2Ru5(CO)16(C) | 90 | 76 | 7 | M-5-7-76-A | |
| Os5(CO)19 | 90 | 78 | 6 | M-5-6-78-H | |
| Os5(CO)18 | 90 | 76 | 7 | M-5-7-76-A | |
| H2Os5(CO)16 | 90 | 74 | 8 | M-5-8-74-N | |
| Os5(CO)16 | 90 | 72 | 9 | M-5-9-72-C | |
| Os5(CO)17 | 90 | 74 | 8 | M-5-8-74-N | |
| Fe6(C)(CO)162- | 108 | 86 | 11 | M-6-11-86-C | |
| H2Ru6(CO)18 | 108 | 86 | 11 | M-6-11-86-C | |
| Ru6(CO)182- | 108 | 86 | 11 | M-6-11-86-C | |
| Ru5Pt(C)(CO)152- | 108 | 86 | 11 | M-6-11-86-C | |
| Ru5Co(C)(CO)12– | 108 | 78 | 15 | M-6-15-78-C4C | |
| Ru5Co(C)(CO)15– | 108 | 84 | 12 | M-6-12-84-C1C | |
| Ru6(C)(CO)17 | 108 | 86 | 11 | M-6-11-86-C | |
| Os6(CO)18 | 108 | 84 | 12 | M-6-12-84-C1C | |
| Os6(H)2(CO)19 | 108 | 88 | 10 | M-6-10-88-N | |
| Os6(CO)18L | 108 | 86 | 11 | M-6-11-86-C | |
| Os6(CO)18L2 | 108 | 88 | 10 | M-6-10-88-N | |
| Os6(CO)18L3 | 108 | 90 | 9 | M-6-9-90-A | |
| Os6(CO)18L4 | 108 | 92 | 8 | M-6-8-92-H | |
| Os6(P)(CO)18– | 108 | 90 | 9 | M-6-9-90-A | |
| Ru4Au3(CO)12L (L=PPh3) | 126 | 88 | 19 | M-7-19-88-C6C | |
| Ru7(CO)202- | 126 | 98 | 14 | M-7-14-98-C1C | |
| Ru7(CO)15(P)L2– | 126 | 98 | 14 | M-7-14-98-C1C | |
| L= PPh3 | |||||
| Ru5Pt(C)(CO)152- | 126 | ||||
| Os7(CO)21 | 126 | 98 | 14 | M-7-14-98-C1C | |
| Os7(H)2(CO)20 | 126 | 98 | 14 | M-7-14-98-C1C | |
| Os6Rh(H)9(CO)18 | 126 | 102 | 12 | M-7-12-102-N | |
| Os7(CO)21 | 126 | 98 | 14 | M-7-14-98-C1C | |
| Os7(H)2(CO)21 | 126 | 100 | 13 | M-7-13-100-C | |
| Os6Rh(H)9(CO)18 | 126 | 102 | 12 | M-7-12-102-N | |
| Ru6Cu2(C)(CO)16L2 | 144 | 110 | 17 | M-8-17-110-C2C | |
| L=NC-CH3 | |||||
| Ru8(H)2(CO)212- | 144 | 110 | 17 | M-8-17-110-C2C | |
| Ru8(C)2(CO)17L2* | 144 | 110 | 17 | M-8-17-110-C2C | |
| Ru8(P)(CO)22– | 144 | 114 | 15 | M-8-15-114-C | |
| Os8(CO)222- | 144 | 110 | 17 | M-8-17-110-C2C | |
| Ru10(C)(CO)242- | 180 | 134 | 23 | M-10-23-134-C4C | |
| Os10(C)(CO)242- | 180 | 134 | 23 | M-10-23-134-C4C | |
| Os10(H)4(CO)242- | 180 | 134 | 23 | M-10-23-134-C4C | |
| Ru6Pd6(CO)242- | 216 | 158 | 29 | M-12-29-158-C6C | |
| Ru10Pt3(C)2(CO)312- | 234 | 182 | 26 | M-13-26-182-C1C |
Comparison Between the K-Value(Number Theory) Approach and the Polyhedral Skeletal Electron Pair Theory Approach
The results obtained from using the number theory approach are in agreement with the results obtained polyhedral skeletal electron pair theory approach. This is best illustrated by applying the empirical formula k = ½ (E-V) on the same examples that are given on the website19 on polyhedral skeletal pair theory (PSEPT).
Rh6(CO)16; E = 6×18 = 108, V= 9×6+16×2 = 86, k = ½ (108-86) = 11. Hence the cluster code is M-6-11-86. When this is checked on the cluster table, it shows that it is a member of CLOSO families with an octahedral symmetry(S-1). Another example is Pb102-; E = 10×8 = 80, V = 40+2 = 42, k = 19. The code is M-10-19-42. This is equivalent to the code M-10-19-142 on transition metal cluster table. When this code is checked on the table 1, the cluster is also a member of the CLOSO families. Thus, its proper code is M-10-19-42-C (main group elements). The shape is not easy to deduce from the k-value of 19. But having two linked square pyramids is a suspect. The next is an S42+ cluster with k = 5 and V = 22. Its code is M-4-5-22 or M-4-5-62 on transition metal table. This corresponds to ARACHNO families. The postulated shape of the cluster is sketched below(S-2).Since S-2 can portray resonance, the shape is expected to be a regular square planar.Theborane ion, B5H54-; E = 40, V = 24, and k = 8. Its code is M-5-8-24 (main group) and this corresponds to M-5-8-74. The cluster belongs to the NIDO families. It has the shape of a square pyramid of 8 linkages(S-3).The ideal symmetry will be C4v. The P4 molecule has a k =6 with a tetrahedral shape (Td). Its code classification is M-4-6-20-N(S-4) which corresponds to M-4-6-60-N on the transition metal cluster table.
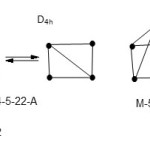 |
Scheme 6 Click here to View scheme |
Other examples include the following. P4S3; E = 7×8 =56,V = 5×4 +6×3 =38, k = ½ (E-V) = ½ (56-38) = 9. The cluster code is M-7-9-38. When checked on the table of the main group elements (not included) it belongs to the members of the K families. The shape of the cluster may be regarded as being derived from the P4 tetrahedral symmetry with the S atoms embedded within the there of the P4 linkages(S-5). The structure of P4O6 (k = 12, S-6), may also be regarded as derived from the P4 shape with the six oxygen atoms embedded in the six bonds of the P4 tetrahedron as for S8 (k = 8) and this is sketched in S-7.
The last example is a hydrocarbon C6H14; E = 6×8 = 48, V= 6×4+14 = 38, and k = 5. The possible isomers of k = 5 are sketched below (S-8).
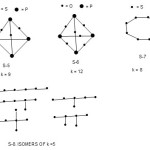 |
Scheme 7 Click here to View scheme |
It is important to note that these structures have been constructed without taking into details the concept of stereochemistry but only following the flow of the k-value.
It is fascinating and amazing that these structures can joyfully and easily be achieved without any knowledge about the 4n, 5n and 6n rules of the polyhedral skeletal electron pair theory.It remains to be seen whether this simple number theory approach can be extended to explain large clusters.
Conclusion
The expanded cluster table is extremely useful for rapid and categorization of molecules or clusters in which skeletal elements obey the octet or eighteen electron rule into the type of cluster series they belong. The table covers a wide range of molecules and clusters where the octet and eighteen electron rules operate. In principle, the cluster table covers all systems in which two or more skeletal elements are embedded. When the k value of a cluster of a known number of skeletal elements and total valence electrons has been calculated, then this information in a form of a code is traced on the cluster table until its position on the table is identified. For instance if the code is M-4-6-60 for a transition metal carbonyl cluster, then one has to follow the M-4 diagonal or ‘HIGH WAY’until a slot of M-4-60 is found in the table. This particular slot represents all members of the nido series with 4 metal atoms an 60 total valence electrons. Since the k value for molecules such as, C2(k =4), N2 (k =3), O2( k = 2), and P4(k = 6) represent genuine chemical bonds that link up these molecular systems, we can regard the k value as representative of electron pairs that are needed to glue up the skeletal elements in clusters which obey the octet or eighteen electron rule. Since the difference in electron count between an element that obeys the octet rule and the one that obeys the 18-electron rule is 10, then cluster table for transition metal carbonyls can be utilized to analyze clusters of the main group elements. Thus, the slot of code M-4-6-60 in transition metals will correspond to the slot of M-4-6-20 in the main group elements. The electron count has been scaled down by the count difference of 10 for each of the 4 elements. The reverse can be done in utilizing the cluster table of the main group elements for the analysis of transition metal carbonyl clusters. This knowledge complements the existing knowledge on cluster theory.
References
- Wade, K, J. Chem. Soc., Dalton, 1971, 792-793.
- Mingos, D. M. P., Nature Physical Science, 1972, 236, 99-102.
- Welch, A. J, Chem. Comm., 2013, 49, 3615-3616.
- Wade, K. Adv. Inorg. Chem. Radiochem. 1976, 18, 1-66.
- Girolami, G. Lecture notes, 2008.
- Gillespie, R. J., Nyholm Memorial Lectures, Chem. Soc. Rev., 1979, 8(3), 315-352.
- Mingos, D. M. P., Acc. Chem. Res.1984, 17(9), 311-319.
- Jemmis, E. D., J. Am. Chem. Soc., 2001, 123(18), 4313-4323.
- Jemmis, E. D., Balakrishnarajan, M. M.,Pattath, D., Chem. Rev, . 2002, 102(1), 93-144.
- King, R. B., Inorg. ChimicaActa, 1986, 116, 99-107.
- Kiremire, E. M. R., Daniel, L. S., Hishimone, P. , Oriental J. Chem., 2014, 30(3), 923-932.
- Kiremire, E. M. R., 2014, 30(3), 1055-1060.
- Kiremire, E. M. R., submitted elsewhere for publication consideration.
- Shaik, S., Danovich, D., Wu, W., Su, P., Rzepa, H. S. Hiberty, P. C. , Nature Chemistry, 2012, 4, 195-200.
- Greenwood, Earnshaw, ‘Chemistry of the elements’, 2nd Edition, Butterworth, Oxford, 1998, 589-590.
- Cotton, F. A. , Wilkinson, G., ‘Advanced Inorganic Chemistry’,4th Edition, John Wiley & Sons, New York, 1980.
- Zanello, P. in ‘Unusual Structures and Physical Properties’, Edited by Glein, M.,Gielen, M, Willen, R., Wrackmeyer, John Wiley and Sons, New York, 2002.
- Hughes, A. K. Wade, K. Coord. Chem. Rev., 2000, 197, 191-229.
- En.wikipedia/polyhedral_ skeletal_ electron: pair20._theory, downloaded, 12-11-2014.

This work is licensed under a Creative Commons Attribution 4.0 International License.









