Rheological Behavior of Biodegradable Lubricants

Introduction

The rheological properties of oils depend on several factors including temperature, shear rate, concentration, density, pressure, application time, chemical properties, additives and catalysts, molecular weight, degree of unsaturation of fatty acids, melting point.^1-3 Most research has focused on studying the effects of temperature, shear rate, concentration and pressure. The most important factor affecting viscosity is temperature. The viscosity of oils and fats decreases with.^4,5 Wan Nik, Ani, Masjuki and Eng Giap⁶ evaluated the effects of shear rate and temperature on the rheological properties of sunflower, corn, canola, coconut and superolein vegetable oils. The effects of shear temperature and velocity were studied by comparing some parameters obtained through four rheological models. It has been found that the viscosity decreases with the increase in temperature at all the studied oils, the influence of the temperature on the change in viscosity being stronger than the effect of the shear rate. It has been established that sunflower oil has the best stability of viscosity with temperature variation. Heating and maintaining oils at high temperatures is a process that causes a series of chemical reactions that occur in the oil, generating a multitude of chemical compounds.⁷ Satyanarayana and Muraleedharan⁸ studied viscosity variation with temperature rise for palm kernel oil and rubber oil seed oil. In the case of oil from the rubber tree seeds, a more pronounced decrease of the viscosity with the temperature was observed than with the oil obtained from the palm kernels. In the paper,⁹ Campanela determined the viscosity variation with temperature and shear shear variation with the shear rate for sunflower oil, soybean oil, and high oleic sunflower oil. From the analysis of the obtained data it results that between the three oils there are very small differences in the viscosity evolutions with the temperature and the shearing stress with the shearing speed. A study¹⁰ on temperature viscosity variation for soybeans, sunflower, olives, peanuts, canola and corn has highlighted that soybean oil has the slightest variation in viscosity with temperature, followed by the corn, canola oil, hazelnut oil, sunflower oil, while olive oil has the largest variation. A comparative study of viscosity variation with temperature and shear rate for rapeseed oils obtained at various stages of manufacture was carried out in the papers.¹¹ Different differences in viscosity variations with temperature and shear velocity were noted. Yilmaz¹² analyzed the rheological behavior of sunflower oil, soybean oil, peanut oil and a vegetable oil of vegetable origin. At 20°C, peanut oil has the highest viscosity, followed largely by worn oil and sunflower oil, the lowest viscosity is obtained with soybean oil. With the increase in temperature, the difference between the viscosity of the peanut oil and the viscosity of the other oils is getting smaller and the differences in the viscosities of the four vegetable oils are insignificant at 120°C. In the literature, there are four shear stress shear patterns. These are^13-14:

Bingham: t = t_o +η Ý                                                          (1)

Casson: t^1/2 = t_o^1/2 + η^1/2 ý ^1/2                                        (2)

Ostwald-de Waele: t = k ⁿ                                                (3)

and Herschel-Bulkley: t = t_o + kηⁿ                                (4)

where t is the shear stress, t_o – yield stress, η – viscosity,  ý – shear rate, n – flow index and k – index of consistency.

The present paper comprises three shear stress shear stress equations for three types of oils in the temperature range 313-373K.

Material and methods

The rheological behaviour of oils (sunflower, soybean and coconut) was determined using a Haake VT 550 Viscotester developing shear rates ranging between 3 and 120 s^-1 and  measuring viscosities from 10⁴ to 10⁶ mPa.s when the HV₁ viscosity sensor is used. The temperature ranged between 313 and 373K. The accuracy of the temperature was 0.1°C.

Results and Discussion

Figures 1, 2, 3, 4, 5, 6 and 7 show the shear shear shear shear shear shear in the temperature range 313-373K. The graphs show a linear shear stress shear rate at all the temperatures at which the three types of biodegradable oils were studied: oil soybean oil, sunflower oil  and coconut oil.

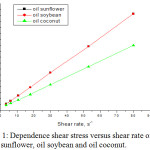Figure 1: Dependence shear stress versus shear rate of 313K for oil sunflower, oil soybean and oil coconut. Click here to view figure

 

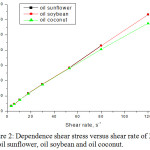Figure 2: Dependence shear stress versus shear rate of 323K for oil sunflower, oil soybean and oil coconut. Click here to view figure

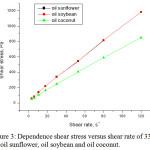Figure 3: Dependence shear stress versus shear rate of 333K for oil sunflower, oil soybean and oil coconut. Click here to view figure

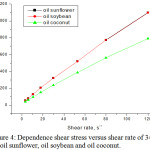Figure 4: Dependence shear stress versus shear rate of 343K for oil sunflower, oil soybean and oil coconut. Click here to view figure

 

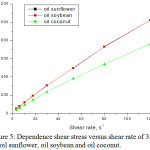Figure 5: Dependence shear stress versus shear rate of 353K for oil sunflower, oil soybean and oil coconut. Click here to view figure

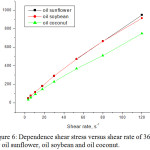Figure 6: Dependence shear stress versus shear rate of 363K for oil sunflower, oil soybean and oil coconut. Click here to view figure

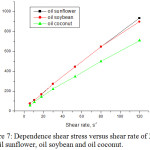Figure 7: Dependence shear stress versus shear rate of 373K for oil sunflower, oil soybean and oil coconut. Click here to view figure

 

This paper presents three shear stress shear stress ratios other than those found in the literature, applied to the experimental data for the three lubricating oils. Equation (5) shows the linear shear stress shear shear rate for the studied oils. Equation (6) shows the polynomial dependence of the shear stress on shear velocity and equation (7) shows the exponential dependence of the two sizes.

t = a+ b ý                                                                               (5)

τ = a +b ý+c² ý                                                                     (6)

τ = τ₀ +a exp(-ý/b)                                                               (7)

Table 1: Correlation constants for rheological model (eq.5) at different temperature ranging from 313 K to 373K for oil sunflower, oil soybean and oil coconut.

T(K)	Oil sunflower			Oil soybean			Oil coconut
	a	b	R2	a	b	R2	a	b	R2
313	19.8184	40.8707	0.9999	19.8298	39.2877	0.9999	13.2248	40.2204	0.9999
323	10.1966	41.1761	0.9999	10.2058	40.7291	0.9998	9.3029	53.5341	0.9991
333	9.6028	38.8397	0.9997	9.6248	38.6389	0.9997	6.8709	35.2977	0.9996
343	8.9793	38.9844	0.9994	8.9593	38.9844	0.9994	6.4601	32.7716	0.9989
353	8.4015	38.2732	0.9989	8.4149	38.2984	0.9989	6.2037	33.5156	0.9984
363	7.7244	39.4742	0.9988	7.4829	44.6587	0.9975	6.0586	30.4246	0.9987
373	7.5876	33.0866	0.9997	7.3621	37.9352	0.9987	5.7591	31.3709	0.9985

 

Tables 1, 2, 3, 4, 5 and 6 show the correlation coefficients for the three equations, parameters a, b, c and t0 for sunflower, soybean and coconut oils in the temperature range 313-373K.

Parameter a of equation (5) decreases with increasing temperature in order of sunflower oil, soybean oil and the lowest values are for coconut oil.

Paraffin b in equation (5) decreases as the temperature increases with the order of sunflower oil, soybeans and the last one is coconut oil.

Table 2: Correlation constants for rheological model (eq.6) at different temperature ranging from 313 K to 373K for oil sunflower, oil soybean and oil coconut.

T(K)	Oil sunflower				Oil soybean
	a	b	c	R2	a	b	c	R2
313	19.3353	45.7115	0.0059	0.9999	19.4858	42.7344	0.0042	0.9999
323	10.2639	40.2711	-5.7430E-4	0.9997	10.1825	41.0424	1.9877E-4	0.9997
333	10.2066	30.7204	-0.0051	0.9997	10.2294	30.5093	-0.0052	0.9997
343	10.0254	24.9179	-0.0089	0.9998	10.0054	24.9179	-0.0089	0.9998
353	9.7546	20.0791	-0.0115	0.9999	9.7881	19.8339	-0.0117	0.9999
363	9.0146	22.1259	-0.0110	0.9998	9.4227	18.5760	-0.0166	0.9999
373	8.2755	23.8375	-0.0059	0.9999	8.6850	20.1464	-0.0113	0.9999

 

Parameter c in equation (6) has varable values in the temperature range in which the oils were studied.

Table 3: Correlation constants for rheological model (eq.6) at different temperature ranging from 313 K to 373K for oil coconut.

T(K)	Oil coconut
	a	b	c	R2
313	12.8963	43.5113	0.0040	0.9999
323	10.6671	35.1924	-0.0116	0.9998
333	7.4791	27.1191	-0.0052	0.9999
343	7.5201	18.5188	-0.0090	0.9999
353	7.4381	16.9179	-0.0105	0.9998
363	6.9155	18.9028	-0.0073	0.9989
373	6.8045	17.3143	-0.0089	0.9994

 

The parameter τ₀ in equation (7) has positive and negative values in the temperature range in which the three types of oils were studied. The values of all parameters depend on the chemical structure of the oil and their non-Newtonian behavior. Correlation coefficients have values close to the unit for all three equations and types of oils.

Table 4: Correlation constants for rheological model (eq.7) at different temperature ranging from 313 K to 373K for oil sunflower, oil soybean and oil coconut.

T(K)	Oil sunflower
	a	b	τ0	R2
313	2.1255E7	-1.0725E6	-2.1255E7	0.9999
323	8627.1730	-88566.7122	88606.9697	0.9997
333	921.9126	-9428.5756	9459.1153	0.9997
343	499.1903	-5031.0308	5055.5401	0.9998
353	3581.1579	-3561.7138	3581.1579	0.9999
363	343.6805	-3135.5209	3156.7454	0.9998
373	639.8184	-5314.0908	5337.6778	0.9999

 

Table 5: Correlation constants for rheological model (eq.7) at different temperature ranging from 313 K to 373K for oil soybean.

T(K)	Oil soybean
	a	b	τ0	R2
313	1.12732E6	-2.2355E7	2.2355E7	0.9999
323	184164.8537	-1.8801E6	1.8801E6	0.9997
333	923.0815	-9461.4239	9491.7546	0.9997
343	498.0696	-5009.8352	5034.3435	0.9998
353	357.3468	-3529.6679	3548.8614	0.9999
363	59.7904	-949.3085	912	0.9658
373	325.5386	-2856.4450	2875.9804	0.9999

 

Table 6: Correlation constants for rheological model (eq.7) at different temperature ranging from 313 K to 373K for oil coconut.

T(K)	Oil coconut
	a	b	τ0	R2
313	1.21772E6	-1.6104E7	1.6104E7	0.9999
323	392.5387	-4226.5564	4260.9162	0.9998
333	654.6927	-4914.0213	4940.9153	0.9999
343	353.7665	-2686.8066	2704.7599	0.9999
353	288.2036	-2178.4783	2194.4185	0.9999
363	222.6809	-2147.1985	2164.1389	0.9999
373	61.8571	-736.1542	708.0000	0.9617

 

Conclusion

 

The vegetable oils used in this study are: oil sunflower, soybean oil and coconut oil. The rheological study was based on graphical representation of shear velocity based on shear stress using experimental data. The rheological models found in the literature are: Bingham, Casson, Ostwald-de Waele and Herschel-Bulkley. The article proposes three other rheological models of shear speed dependence on shear speed. The three oils have a non-Newtonian behavior within the timeframe in which they were studied.

References

1. Revwolinski, C.; Shaffer, D. L.; Journal of the American Oil Chemisis ‘ Society 1985, 62, 1120-1124.
2. Toro-Vazquez, J. F.; Infante-Guerrero, R.; Journal of the American Oil Chemisis ‘ Society 1993, 70, 1115-1119.
3. Diaz, R. M.; Bernardo, M. I.; Fernandez, A. M.; Folgueras, M. B.; Fuel 1996, 75, 574-578.
4. Eromosele, C. O.; Paschal, N. H.; Bioresour. Technol. 2003, 86, 203–205.
5. Hasan, S. W.; Ghannamb, M.; Esmail, N.; Fuel 2010, 89, 1095–1100.
6. Wan Nik, W.; Ani, F. N.; Masjuki, H. H.; Eng Giap, S. G.; Industrial Crops and Products 2005, 22, 249-255.
7. Belitz, H. D.; Grosch, W.; Schieberle, P.; Food Chemistry, 4th revised and extended Edition, Springer-Verlag, Berlin, ISBN 978-3-540-69933-0, 2009.
8. Satyanarayana, M.; Muraleedharan, C.; Energy 2011, 36, 2129-2137.
9. Campanella, A.; Rustoy, E.; Baldessari, A.; Baltanas, M.; Bioresource Technology 2010, 101, 245-254.
10. Franco, Z.; Nguyen, Q. D.; Fuel 2011, 90, 838-843.
11. Ştefănescu, I.; Calomir C.; Gheorghieş, C.; Spânu, C.; The Annals of ”Dunărea de Jos” University of Galaţi, Fascicle VIII Tribologie 2005, ISSN 1221-4590, 3–7.
12. Yilmaz, N.; Biomass and Bioenergy 2011, 35, 2936-2938.
13. Stanciu I.;  Oriental Journal of Chemistry 2015, 31(3), 1383-1387.
14. Stanciu I.;  Oriental Journal of Chemistry 2015, 31(4), 2017-2023.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.