Inhibitory Reactivity of Capsaicin with α-Amylase and α-Glucosidase Related to Antidiabetes using Molecular Docking and Quantum Calculation Methods

Introduction

Nowadays, diabetes is known as the most dangerous disease killing more people than cancer and AIDS combined. Actually, it is said to be a modern disease, and has traditionally been viewed as a disease of rich countries.¹ Around 3.2 million individuals in Thailand have diagnosed currently being diabetes. Thai people are expected to fall in this disease over than 4.3 million in 2035.² Diabetes is caused by a metabolic disorder, in which the body cannot properly store and expense the energy found in food.^3,4 Two main types of diabetes are type I and type II diabetes.^5,6 Type I diabetes is dominant when the body’s immune system attacks the cells in the pancreas that generate insulin. Type II diabetes is the other when the body does not produce enough insulin, or the cells ignore the insulin.^7,8 One of therapeutic approach for diabetes is to control the blood sugar level by the process of an inhibition of carbohydrate hydrolyzing enzymes such as α-amylase and α-glucosidase.^9–13

α-Amylase and α-glucosidase inhibitors can help individual case with type II diabetes by preventing the digestion of carbohydrates such as starch.¹⁴ Carbohydrates are normally converted into simple sugars or monosaccharides, which can be absorbed through the intestine¹⁵. The known natural inhibitors of digestive enzymes include phenolic compounds, anthocyanins, terpenoids and others.^16,17 They operate through various mechanisms. A acarbose, miglitol and voglibose are the commercially available drugs that inhibit pancreatic α-amylase and α-glucosidase in the small intestine (Fig. 1a). The side effects of both enzymatic inhibitors are flatulence, low blood sugar and hepatitis. In recent years, a variety of research has been done on plants. In addition, several herbs and fruits have the property of inhibitors.^18-21

Chili peppers are very well-known economic fruit routinely consumed in many tropical countries. One of the plant’s products is chili peppers of genus Capsicum and belongs to the Solanaceae family. The five domesticated species of chili peppers include Capsicum annuum, Capsicum frutescens, Capsicum chinense, Capsicum pubescens, and Capsicum baccatum.²² Capsaicinoids are the chemicals, which give the rise in heat level of the chilli. They present in almost chilli fruits. The two majorities of capsaicinoids presenting in most varieties of the spice from hot chilli peppers are capsaicin (8-Methyl-N-vanillyl-6-nonenamide) and dihydro-capsaicin (8-Methyl-N-vanillylnonanamide) as shown in Fig. 1b & Fig. 1c, in which capsaicin consists of about 69% and dihydrocapsaicin consists of about 22% of the fruits.²³ The distinctive properties of capsaicinoids in food are such pungent additives. In pharmaceutical industries, they are used for the treatment of pain and inflammation in different kinds of diseases.

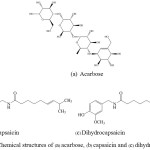Figure 1: Chemical structures of (a) acarbose, (b) capsaicin and (c) dihydrocapsaicin. Click here to View figure

 

The Protein Data Bank (PDB) (RCSB PDB) is the depository for crystal structures of biological macromolecules from the experiment. Currently, the PDB provides X-ray crystallography of more than 112,968 crystal structures from 1971 to 2015. In addition, the crystal structures of α-amylase and α-glucosidase are available in the PDB of more than 334 and 183 crystal structures, respectively. The PDB codes of the crystalline structure of the wild-type of α-amylase complex and α-glucosidase complex are 3OLD and 3 TOP, respectively, which are introduced for this study.

Auto Dock program has been widely used and is the most cited docking software. It is very fast, provides high quality predictions of ligand conformations, and good correlations between predicted inhibition constants and experimental ones. In addition, AutoDockTools is a software used to prepare the input files for Auto Dock.²⁴ In order to understand deeper in the molecular interactions between the inhibitor and the residues in any binding pocket which is not observed by an experiment, theoretical investigation has thus been an alternative method to investigate the enzyme and inhibitor interaction in details for large molecular system. Recently, quantum chemical calculations were used to study the effect of mutation related to inhibitor resistant. It was found that the calculations are significant for guiding the cause of resistant.²⁵

The present study aims to evaluate capsaicin whether it can inhibit both α-amylase and α-glucosidase in human compared with acarbose. Then, the particular interactions between these inhibitors with individual residues in binding site of both enzymes have been investigated. The scope and limitation of this study composes of (1) investigating the binding free energy and inhibition constant between inhibitors (capsaicin and acarbose) and enzymes (α-amylase and α-glucosidase) by using a molecular docking method, and (2) calculating the interaction between the inhibitors and amino acids in active site of the enzymes by using quantum mechanics calculation.

The objectives of the study are (1) to evaluate the inhibitory activity of capsaicin and acarbose (for comparison) on α-amylase and α-glucosidase; (2) to investigate the optimum conditions for docking of α-amylase and α-glucosidase; (3) to calculate the interaction between the inhibitors (acarbose and capsaicin) and amino acid in the binding pocket of the enzymes (α-amylase and α-glucosidase) based on the quantum chemical calculations at MP2/6-31G(d,p) level; and (4) to investigate the main interactions between the amino acid residues in the binding site of both enzymes and the inhibitors contributing to the inhibitory efficiency.

α-Glucosidase and α-amylase inhibitors are found in microorganisms, plants and animals.^26,27 Capsaicin, an alkaloid or capsaicinoids, is the principal pungent and irritating constituent of hot chilli peppers that are widely used as food additives and possess antimicrobial properties.²⁸ Several instrumental techniques have been used for the structural insights of capsaiciniods including molecular docking,^29,30 molecular dynamics simulation,^31,32 homology modeling,^33,34 virtual screening,^35,36 and bioassay validations.³⁷

Recently, molecular docking has mostly been used for capsaicinoid analysis because of its rapidness and reliability. Molecular docking is one of the modeling techniques used to determine the position docking of capsaicinoids in the binding pocket of enzymes.³⁸ Amylase, maltase and sucrase are the enzymes that digest carbohydrate found in the alimentary canal. Amylases are one of the main enzymes used in industry. Amylase has been reported to occur in microorganisms, although they are also found in plants and animals. Two major classes of amylases have been identified in microorganisms, namely α-amylase and glucoamylase. α-Amylases (endo-1,4-α-D-glucan glucohydrolase, E.C. 3.2.1.1) are extracellular enzymes that randomly cleave the 1,4-α-D-glucosidic linkages between adjacent glucose units in the linear amylose chain.³⁹ α-Amylase is the enzyme responding for the hydrolysis of starch and carbohydrates to monosaccharides.⁴⁰ Amylase is found in saliva and small intestine by synthesizing from pancreas. The functional activity of amylase is to break down α-glycosidic bond in starch to be maltose, glucose and dextrin. The inhibition function of α-amylase is beneficial in reducing sugar that your body will absorb it. Currently, medical trend is interested in using amylase inhibitor from natural plant used in treatment of diabetes.

Maltase or also known as α-glucosidase and sucrase or known as invertase work in the area of microvilli in small intestine; glucosidase reaction is well known. Glucosidase inhibitor such as acarbose inhibits both of maltase and sucrase. Thus, in carbohydrate catabolism, disaccharide sugars cannot digest to monosaccharide ones. As a result, it reduces the sugar absorption to the blood system. Glucosidases are glycosidic hydrolase enzymes categorized under the EC number 3.2.1.20 which have also been found in microorganisms.

α-Amylases are universally distributed throughout the animal, plant and microbial kingdoms. Two kinds of α-amylase are produced by many mammals, saliva α-amylase from the parotid gland and the pancreatic α-amylase from the pancreas.⁴¹ α-Amylase (AIs) and α-glucosidase (AGIs) inhibitors are widely used in the treatment of patients with type II diabetes. Diet and exercise are the first step in its treatment. But if these measures alone fail to sufficiently control blood glucose levels, starting oral drug therapy is recommended.⁴² α-Glucosidase and α-amylase inhibitors are classified into the two major groups as proteinaceous and non-proteinaceous inhibitors.

One benefit of hot chili peppers is therapeutic approach for treating diabetes which decreases the postprandial hyperglycemia. This is done by retarding the absorption of glucose through the inhibition of carbohydrate hydrolyzing enzymes, α-glucosidase and α-amylase, in the digestive tract.⁴³ The control of postprandial hyperglycemia is an important strategy in the management of diabetes mellitus, especially type II diabetes mellitus (2DM), and reducing chronic complications associated with the disease.^44-46  Hence, the inhibition of enzymes (α-amylase and α-glucosidase) involved in the digestion of carbohydrates can significantly decrease the postprandial increase of the blood glucose after a mixed carbohydrate diet, by delaying the process of carbohydrate hydrolysis, absorption, phenolic phytochemicals from spices and have shown promising potentials.^47,48 Presently, the computational studies have not been reported yet about the inhibitory effect of the enzymes by using capsaicinoids as inhibitors.

The non-proteinaceous α-amylase and α-glucosidase inhibitors contains diverse types of organic compounds such as acarbose, acarbose analogues, hibiscus acid, tannins, flavonoids and glucopyranosylidene-spiro-thiohydantoin. α-Glucosidase inhibitors (AGIs) reversibly inhibits a number of a-glucosidase enzymes (e.g. maltase), consequently delaying the absorption of sugars from the gut.⁴⁹ In a recent study among healthy subjects it was suggested that the therapeutic effects of AGIs are not only based on a delayed digestion of complex carbohydrates, but also on metabolic effects of colonic starch fermentation.⁵⁰ Acarbose (Glucobay^®) is the most widely prescribed AGI. The other AGIs are miglitol (Glyset^®) and voglibose (Volix^®, Basen^®). AGIs might be a reasonable option as first-line drug in the treatment of patients with DM2 as it specifically targets postprandial hyperglycemia, a possible independent risk factor for cardiovascular complications.⁵¹ Although rare cases of hepatic injury are described, AGIs are expected to cause no hypoglycemic events or other life-threatening events, even at overdoses, and cause no weight gain.⁵² The a-amylase inhibitor contains diverse types of organic compounds as mentioned above. The inhibitory activity of these compounds against a-amylase is due in part to their cyclic structures, which resemble substrates at catalytic sites of a-amylase.⁵³

A number of docking programs have been developed during the last two decades and made available to academic institutions at little or no charge. Basic characteristics such as supported platforms, license terms, as well as applied docking algorithms and scoring functions are presented. DOCK 1.0⁵⁴ was the first automated receptor-ligand docking program. It was designed in 1982 by Irwin Kuntz in Department of Pharmacology at the University of California at San Francisco. At present, there are at least a dozen docking tools in the market, the most commonly used being: AutoDock,⁵⁵ DOCK,⁵⁶ FlexX,⁵⁶ GOLD,⁵⁷ LigandFit⁵⁸and the relatively new tools: Glide,⁵⁹ FRED⁶⁰ and the youngest Surflex.⁵⁴

Molecular Docking

Molecular docking is a computational method used to study the formation of intermolecular complexes of one smaller molecule (called ligand) with a larger molecule (called receptor), which usually is a protein of known three-dimensional structure. Different types of interactions between the molecules can be distinguished: protein-protein, protein-DNA, DNA-ligand and protein-ligand.⁶¹  For an enzyme and inhibitor, docking aims at correct prediction of the structure of the complex under equilibrium conditions, expressed as equation (1):

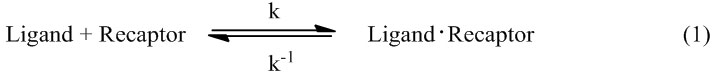
The particular interest is the free energy of binding (∆G_binding) expressed as

∆G_binding = G_cpx  –  G_ligand  –  G_receptor                             (2)

where, G_cpx, G_ligand and G_receptor are free energy of complex, ligand and receptor, respectively.

The free energy of binding is related to binding affinity as shown in equations (3) and (4);

∆G_binding= -RT (ln 1/ Ki )                       (3)

Ki = e ∆G/RT                                             (4)

where, R is 1.987 cal·K^–1·mol^–1, T is absolute temperature (K), and K_i is inhibitor constant.

Molecular docking uses the Monte Carlo simulation (MC) to determine the receptor molecule in place and add ligand into it then calculate energy between ligand and receptor molecule (E₁). Then, change in ligand’s position randomly and calculate for new energy (E₂), if E₂ is less than E₁, a ligand will move to this position after that the ligand will change its position continuously until it reaches specified number of times (for this study, it is 2,500,000 times) or get the lowest energy. The last position of ligand with the lowest energy is called 1 run of docking. In general, docking is performed for 50 runs.

The energy calculation between ligand and receptor is as followed. Firstly, the program makes up grid map for probe atom of ligand. The grid box must cover an active site of receptor molecule as shown in Fig. 2.  Each probe atom of ligand is placed in the upper left corner of the box. Calculation of energy between probe atom and receptor is done, and then this data is stored. The program will calculate continuously through every grid position. Therefore, one gets grid map for each probe atom.

The calculation of energy is done while the stimulation is performed by considering of both probe atom and grid point, and reading the energy value from grid map that relates with the kind and the position of atom in each box, and then combining them together for total energy of the system that consists of ligand and receptor molecules.

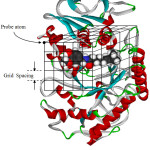Figure 2: Making of a grid map for probe atom. Click here to View figure

 

Molecular Mechanics

Molecular mechanics assumes the steric energy of a molecule to arise from a few specific interactions within a molecule. These interactions include the stretching or compressing of bonds beyond their equilibrium lengths, bending of bond angles, torsional effects of twisting about single bonds, the van der Waals attractions or repulsions of atoms that come close together, and the Coulomb interactions between partial charges in a molecule due to polar atoms. To quantify the contribution of each, these interactions can be modeled by a potential function that gives the energy of the interaction as a function of distance, angle, or charge.^62,63 The total steric energy of a molecule can be written as a sum of the energies of the interactions in equation (5):

V = V_bond + V_angle + V_torsion + V_vdW + V_Coulomb                                                  (5)

where, V is potential energy, V_bond is bond stretching energy, V_angle is angle bending energy, V_torsion is torsional angle energy, V_vdW is van der Waals force, and V_Coulomb is Coulomb force.

Quantum Mechanics

Quantum mechanics or quantum theory is the theoretical basis of modern physics that explains the nature and behavior of matter and energy in the atomic and subatomic level. The nature and behavior of matter and energy at that level is sometimes referred to as quantum physics and quantum mechanics. The development of quantum mechanical techniques is more generally applicable and that can be implemented on a computer. When the properties of such particle (e.g. mass, charge, etc.) are expressed in macroscopic units then the values must usually be multiplied, which are too complication. Several mathematical techniques are applied to these problems for simplification.⁶⁴ The starting point for any discussion of quantum mechanics is the Schrödinger equation. The equation is the basis for most of the computational scientist. It can be solved exactly for only a few problems such as the particle in the box, the harmonic oscillator, the particle on a sphere and the hydrogen atom. One of them has been widely used in the quantum chemical calculation is the Hartree–Fock (HF) model.

Ab Initio

The most common type of ab initio calculation is called Hartree-Fock (HF) calculation, in which the primary approximation is called the mean field approximation.  This means that the Coulombic electron-electron repulsion is not explicitly taken into account, however, its average effect is included in the calculation. This is a variation calculation, which implies that the approximate energies calculated are all equal to or greater than the exact energy. The accuracy of the calculation depends on the size of the basis set used, however because of the mean field approximation, the energies from HF calculations are always greater than the exact energy and tend, with increasing basis size, to a limiting value called the Hartree-Fock limit.

An additional issue that affects the accuracy of the computed results is the form chosen for the basis functions.  The actual form of the single electronic molecular wave function (molecular orbital) is of course not known.  The forms, used for the basis functions, can provide a better or worse approximation to the exact numerical single electron solution of the HF equation. The basis functions used most often are combinations of either Slater type orbitals (exp(–ax)) namely as STO or Gaussian type orbitals (exp (–ax²)), GTO. Molecular orbital is formed from linear combinations of atomic orbitals, which are nothing more than linear combinations of the basis functions with coefficients found from the appropriate atomic HF calculations.  Because of this approximation, most HF calculations give a computed energy greater than the Hartree- Fock limit. The exact set of the basis functions used is often specified by an abbreviation, such as STO-3G or 6-311++g**.  From this aspect, it can be read about structures and features of some popular basis sets.

An alternative ab initio method is the second Møller–Plesset perturbation theory (MP2). MP2 is perhaps the simplest model to take reasonable account of electron correlation, and generally provides accurate descriptions of equilibrium structure, conformation and energetics of a variety of chemical reactions, including reactions where chemical bonds are broken. MP methods are supported for the same basis sets and pseudopotentials available for Hartree-Fock and density functional models.

Semi–empirical

Semi-empirical calculations are set up with the same general structure as a HF calculation. Within this framework, certain pieces of information, such as two electron integrals, are approximated or completely omitted.  In order to correct the errors introduced by omitting these parts of the calculation, the method is parameterized, by curve fitting in a few parameters or numbers, in order to give the best possible agreement with experimental data. The good side of semi-empirical calculations is that they are much faster than the ab initio calculations. The bad side of semi-empirical calculations is that the results can be erratic. If the molecule under study is similar to molecules in the data base used to parameterize the method, the results may then be very good. If this molecule is significantly different from anything in the parameterization set, the answers may be poor. Semi-empirical calculations have been very successful in computational organic chemistry, where there are only a few elements used extensively and the molecules are of moderate size. However, semi-empirical methods have been devised specifically for the description of inorganic chemistry as well.

Materials and Methods

Program Tools and Instruments

There are five program tools including AutoDockTools-1.5.6 (ADT), AutoDock 4.2, HyperChem 8.0, Weblab Viewer Pro 4.0 and Gaussian 09. In this study, all calculations were performed using computer cluster located at Department of Chemistry, Faculty of Science, Khon Kaen University, and National Electronics and Computer Technology Center (NECTEC), Bangkok (supported by National e-Science Infrastructure Consortium).

Molecular Docking

Molecular docking is a computer–based method which predicts the preferred orientation of one molecule to a second when bound to each other to form a stable complex. The aim of molecular docking is to predict the interaction between two molecules. Its ultimate goal is to find the most stable conformation between ligand and protein. The procedure of docking consists of three important steps: binding site identification and characterization, orientation of the ligand within the binding site, and evaluation of the orientation for appropriateness of fit. A stepwise process for molecular docking is shown in Fig. 3.

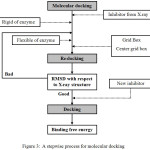Figure 3: A stepwise process for molecular docking. Click here to View figure

 

Ligand set up

For capsaicin, it was generated by using HyperChem-8.0 program (Hypercube, 2007), and then optimized with PM3 semi-empirical level, and saved as hin file format. For acarbose, the X-ray structure was downloaded from the Protein Data Bank (PDB code: 3TOP) complexed with α-glucosidase. Acarbose molecule was separated and then missing hydrogen atoms were added and their geometries were optimized with MM+ forcefield using HyperChem 8.0. The final structure was also saved as hin file. The hin file was then converted to pdb file format through Babel in Linux. After loading the pdb file into ADT, the atomic charges were assigned with Gasteiger charge and then the rotatable bonds were defined and saved as pdbqt file.

For acarbose, all hydroxyl bonds were assigned as rotatable bond, totally 13 bonds, whereas for capsaicin, the rotatable bonds were assigned for 4 sets consisting of one, two, three and four rotatable bonds. These bonds were listed in Table 1 and shown with arrow.

Enzyme set up

The X-ray structures of enzymes were retrieved from the Protein Data Bank (www.rcsb.org). The PDB code of human pancreatic a-amylase is 3OLD, and the PDB code of human a-glucosidase is 3TOP. As the human a-glucosidase is a symmetric dimmer, the chain A of the enzyme was deleted and only chain B was used in the docking. The water molecules in the file were then deleted using Weblab ViewerPro 4.0 program⁶⁵ and the protein file was saved as protein.pdb. Each pdb file was loaded into ADT program, then all missing hydrogen atoms were added to the protein structure, all non-polar hydrogens were merged with carbon atoms, and Gasteiger charge were assigned. When design on molecular calculation, only selected elements in the active site vicinity of the enzyme are fixed to make any interactions within the configuration of its counter ions of the inhibitor used, thus each monomer (A or B) of alpha-glucosidase dimer can be represented for their substrate-enzyme interactions basis. It is done by molecular docking and quantum calculation with each monomer, but does not work for its dimer. Certainly, it would be affect to the calculated results as a whole, if concerning on that particular aspect. However, it is aimed only to point out what really specific interactions can occur between the active of the enzyme and the molecular configuration of the capsaicin. In order to performed flexible protein docking, the rotatable bonds of protein were defined as listed in Table 2. The files were saved as flexible.pdbqt and rigid. pdbqt.

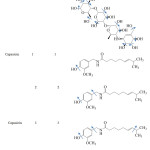Table 1: Conformation of flexible inhibitors. Click here to View table

 

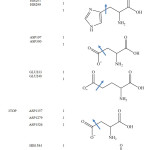Table 2: Conformation of flexible amino acids. Click here to View table

 

Grid Parameter Files

The grid parameter files were prepared for molecular docking by ADT. For re-docking procedure, the grid box was studied at 60×60×60, 66×66×66 and 70×70×70 Å for both 3OLD and 3TOP. The center of grid box was defined as the center of ligand complexed with its enzyme (x = 6.0, y = -16.9, z = -24.4 for 3OLD and x = -51.5, y = 9.0, z = -64.8 for 3TOP), the spacing of grid box was set at 0.375 Å and saved as protein.gpf. Then, these grid parameter files were used to generate the grip map files (with command autogrid4.2 –p protein.gpf –l protein.glg &). The grid map files contain information about the energy between probe atoms and protein at each grid point and were used for docking calculation.

Docking Parameter Files

The docking parameter files were prepared for molecular docking by ADT. The main parameters were energy evalution of 2,500,000 and 50 runs with Lamarckian genetic algorithm search. The default values were used for other parameters. Docking calculations were performed by using AutoDock4.2 program (with command autodock4.2 –p ligand.dpf –l ligand.dlg &).

Quantum Chemical Calculation

Quantum chemical calculations were used to calculate particular interactions of all complex structures. These calculated results can be related to the inhibitory efficiency obtained from molecular docking. Therefore, the quantum chemical calculations are important for investigating molecular interactions in various types of enzymes (a-amylase and a-glucosidase) to inhibitors (capsaicin and acarbose). The complex structures obtained from docking result were employed by selecting amino acids surrounding inhibitors within the inter-atomic distance of 4 Å. The particular interaction energy was focused on the couple of inhibitor and each amino acid. Then, hydrogen atoms were added into the cutting regions using HyperChem 8.0 program and was investigated using Gaussian 09 program (Gaussian, 2013) with MP2/6-31G(d,p) level of calculations.

Conformational and Energetic Properties of the Enzyme and the Inhibitor

The optimal conditions for molecular docking of α-amylase and α-glucosidase enzymes were determined with the re-docking step based on ligand with its enzyme. The docked structures of enzymes and inhibitors were generated using AutoDock4.2 program. Also the binding free energy and inhibition constant were evaluated. The energies such as van der Waals, hydrogen bonding, electrostatic and hydrophobic between enzymes and inhibitors were investigated. Quantum calculations with MP2 method were performed in order to determine the main interactions between the inhibitors and selected amino acids surrounding the inhibitors within the inner-atomic distance of 4 Å.

Results and Discussion

This research aims to evaluate the inhibitory activity of capsaicin on α-amylase and α-glucosidase enzymes in order to search for an alternative diabetes drug. Acarbose, a commercial drug, was also evaluated for comparison. The procedure of the study consists of three main steps: (1) re-docking, (2) docking calculation and (3) quantum calculation. The results and discussion of these steps are as followed.

Re–docking

The re-docking process aims to investigate the optimal conditions used for docking calculations of α-amylase and α-glucosidase. The main conditions or parameters for re-docking are grid box size and number of rotatable bonds of enzymes. As mentioned previously in CHAPTER III, for both enzymes, the grid box size was defined as 60x60x60, 66x66x66 and 70x70x70 ų.  For α-amylase, the grid box center was x = 6.0, y = -16.9, z = -24.4 which was a center of ligand. A number of rotatable bonds were assigned for three sets (0, 3 and 7 bonds). Similarly, for α-glucosidase, the grid center was x = -51.5, y = 9.0, z = -64.8 and rotatable bonds were assigned for two sets as 0 and 4 bonds. The main criteria used to decide the re-docking result is root mean square deviation (RMSD) which is a comparison of ligand position of docked structure and X-ray structure. The acceptable RMSD value must be less than 2.0 Å. The results of re-docking are shown in Table 3 and Table 4. As shown in the tables, the docking results (both ΔG_binding and RMSD values) depend on the number of rotatable bonds and grid box size.

For α-amylase, the rotatable bonds of 3 bonds yielded the RMSD values less than 2.0 Å which is an acceptable value. Considering the grid box size, one found that the box size of 60x60x60 and 66x66x66 ų provided better docking result than the box size of 70x70x70 ų, as seen from the number in cluster value (Table 3). For α-glucosidase (Table 4), both number of rotatable bonds (0 and 4 bonds) resulted the RMSD values less than 2.0 Å, and the number in cluster values were not different. However, the grid box size of 60x60x60 ų and 66x66x66 ų yielded the lowest free energy of binding (about -11.9 kcal/mol) compared with grid box size of   70x70x70 ų. Therefore, one can conclude that 3 flexible residues (for α-amylase) and 4 flexible residues (for α-glucosidase) with grid box size of 60x60x60 and 66x66x66 ų are the suitable conditions for docking calculation. Such condition is shown in Table 5. The re-docked positions of acarbose for both enzymes are shown in Fig. 4-7. One can see that the re-docked positions obtained from grid box size of 60x60x60 ų and that obtained from grid box size of 66x66x66 ų are not significant different and are in agreement with the X-ray structure.

Table 3: The results of re-docking for α-amylase.

Flexible residue		Grid box (Å3)	Number in cluster	ΔGbinding (kcal/mol)	RMSD (Å)
Number of rotatable bond	Amino acid
0	–	60x60x60	29	-3.56	1.33-2.07
		66x66x66	23	-2.44	2.22-2.69
		70x70x70	16	-3.25	1.31-2.06
3	ASP197GLU233ASP300	60x60x60	38	-8.16	1.34-1.49
		66x66x66	35	-8.01	1.35-1.55
		70x70x70	21	-8.17	1.36-1.61
7	HIS101ASP197HIS201GLU233GLU240HIS299ASP300	60x60x60	38	-8.10	1.27-2.08
		66x66x66	29	-8.04	1.38-2.05
		70x70x70	33	-7.85	1.36-2.29

 

Table 4: The results of re-docking for α-glucosidase.

Flexible residue		Grid box (Å3)	Number in cluster	ΔGbinding (kcal/mol)	RMSD (Å)
Rotatable bond	Amino acid
0	–	60x60x60	50	-8.21	1.05-1.40
		66x66x66	50	-8.10	1.03-1.39
		70x70x70	50	-8.01	1.04-1.48
4	ASP1157ASP1279ASP1526HIS1584	60x60x60	50	-11.93	0.95-1.40
		66x66x66	50	-11.90	1.00-1.36
		70x70x70	50	-11.76	0.92-1.37

 

Table 5: Summarized parameters from re-docking.

Enzyme	Flexible residue	Number of rotatable bonds	Grid box (Å3)
α-amylase	ASP197GLU233ASP300	3	60x60x60
			66x66x66
α-glucosidase	ASP1157ASP1279ASP1526HIS1584	4	60x60x60
			66x66x66

 

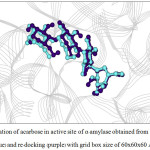Figure 4: Orientation of acarbose in active site of α–amylase obtained from X–ray structure (blue) and re–docking (purple)  with grid box size of 60x60x60 Å3. Click here to View figure

 

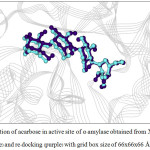Figure 5: Orientation of acarbose in active site of α–amylase obtained from X–ray structure (blue) and re-docking (purple) with grid box size of 66x66x66 Å3. Click here to View figure

 

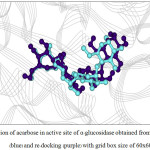Figure 6: Orientation of acarbose in active site of α–glucosidase obtained from X–ray structure (blue) and re–docking (purple) with grid box size of 60x60x60 Å3. Click here to View figure

 

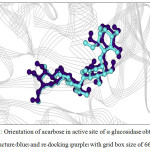Figure 7: Orientation of acarbose in active site of α–glucosidase obtained from X-ray structure (blue) and re-docking (purple) with grid box size of 66x66x66 Å3. Click here to View figure

 

Docking of Capsaicin Compared to Acarbose

Using the suitable parameters as listed in Table 5, the docking calculations of capsaicin with both α-amylase and α-glucosidase enzymes were obtained and shown in Tables 6 and 7, respectively. For α-amylase (Table 6), the docking results depend on the number of rotatable bonds of acarbose. The binding free energy varies from about -5.2 to -6.3 kcal/mol and the number in cluster varies from 21 to 50 runs. Clearly, the best docking result was obtained from 2 rotatable bonds of acarbose yielding the number is cluster of 50 runs, although it provided the ΔG_binding of about 0.5 kcal/mol higher than that of 3 rotatable bonds for both grid box sizes.

Similarly, the docking result of α-glucosidase with capsaicin revealed that 2 rotatable bonds of capsaicin yielded the best docking calculation with the number in cluster of 47 and 34 runs for grid box size 60x60x60 and 66x66x66 ų, respectively, and the ΔG_binding of about -6.1 kcal/mol (Table 7). The docking results of capsaicin compared to acarbose were summarized in Table 8. One found that the binding free energies of acarbose were about 1.4 times (for α-amylase) and about 2 times (for α-glucosidase) larger negative than capsaicin. These results yielded the inhibition constants of less than 1 µM for acarbose and of about 20-50 µM for capsaicin.

In conclusion, the inhibitory activity of acarbose is higher than that of capsaicin. In addition, acarbose and capsaicin can inhibit α-glucosidase better than α-amylase. Considering the docking of inhibitors of 60x60x60 ų compared to grid box size of 66x66x66 ų, one can see that the results (ΔG_binding and K_i) are not significant different. This is not surprise, because the positions of inhibitors obtained from both grid box sizes were not different. Therefore, the docked structures obtained from the grid box size of 60x60x60 ų were employed for further analysis.

Table 6: The binding free energy (ΔG_binding) and inhibition constant (K_i) of α-amylase.

Inhibitor	Grid box (Å3)	Number of rotatable bonds	Number in cluster	ΔGbinding (kcal/mol)	Ki (µM)
Acarbose	60x60x60	13	38	-8.16	0.42
	66x66x66	13	35	-8.01	0.33
Capsaicin	60x60x60	1	25	-5.09	175.56
		2	50	-5.78	45.88
		3	26	-6.25	22.01
		4	23	-5.22	21.74
	66x66x66	1	25	-4.78	175.81
		2	50	-5.78	46.53
		3	20	-6.27	20.74
		4	21	-5.18	22.04

 

Table 7: The binding free energy (DG_binding) and inhibition constant (K_i) of α-glucosidase.

Inhibitor	Grid box (Å3)	Number of rotatable bonds	Number in cluster	DGbinding (kcal/mol)	Ki (µM)
Acarbose	60x60x60	13	50	-11.93	0.0002
	66x66x66	13	50	-11.90	0.0003
Capsaicin	60x60x60	1	35	-5.75	48.92
		2	47	-6.08	23.67
		3	25	-5.73	38.78
		4	25	-6.03	24.66
	66x66x66	1	26	-5.67	51.15
		2	34	-6.08	26.08
		3	31	-5.07	44.84
		4	10	-5.07	22.68

 

Table 8: Summary of the binding free energy (ΔG_binding) and inhibition constant (K_i) obtained from molecular docking.

Inhibitor	Grid box (Å3)	ΔGbinding (kcal/mol)		Ki (µM)
		α-amylase	α-glucosidase	α-amylase	α-glucosidase
Acarbose	60x60x60	-8.16	-11.93	0.42	0.0002
	66x66x66	-8.01	-11.90	0.33	0.0003
Capsaicin	60x60x60	-5.78	-6.08	45.88	23.67
	66x66x66	-5.78	-6.08	46.53	26.08

 

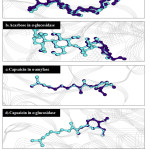Figure 8: The positions of inhibitors in active site of enzymes obtained from molecular docking with grid box size of 60x60x60 Å3 (purple) compared to 66x66x66 Å3 (blue). Click here to View figure

 

Figures 9-12 show the orientation of inhibitors surrounded by amino acids in active site of enzymes. The interactions between the inhibitors and amino acids were classified as (1) hydrogen bond displayed as dash line, (2) π-π interaction and (3) electrostatic interaction (ELEC). Note that, hydrogen bond is the strongest interaction compared to others. These interactions were listed in Table 9 (for α-amylase) and Table 10 (for α-glucosidase). Acarbose can form more hydrogen bonds with amino acids of two enzymes than capsaicin leading to higher inhibition efficiency as mentioned before. This is not surprised, because acarbose composes of many –OH groups that can form hydrogen bond.

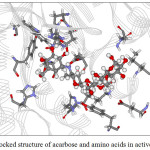Figure 9: The docked structure of acarbose and amino acids in active site of α–amylase. Click here to View figure

 

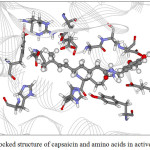Figure 10: The docked structure of capsaicin and amino acids in active site of α–amylase. Click here to View figure

 

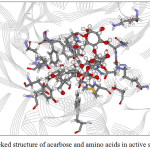Figure 11:The docked structure of acarbose and amino acids in active site of α–glucosidase. Click here to View figure

 

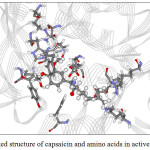Figure 12: The docked structure of capsaicin and amino acids in active site of α –glucosidase. Click here to View figure

 

Table 9: The interaction between inhibitors and amino acids in active site of α-amylase.

Ligand	H–bond	π-π	Electrostatic bond
Acarbose	ARG195 (2.42 Å)	–	TRP58
	ASP197 (1.84 Å)		TYR62
	LYS200 (2.02 Å)		HIS101
	GLU233 (1.69 Å)		TYR151
	ASP300 (1.59 Å)		HIS201
	GLY308 (2.29 Å)		HIS299
			LEU237
			GLU240
			GLY309
Capsaicin	LYS200 (1.92 Å)	–	TYR62
			HIS101
			TYR151
			ARG195
			HIS201
			GLU233
			ASP236
			GLY238
			GLU240
			ASP300
			ALA307

 

Table 10: The interaction between inhibitors and amino acids in active site of α–glucosidase.

Ligand	H–bond	π-π	Electrostatic bond
Acarbose	ASP1157 (1.83 Å)	–	GLN1158
	LYS1164 (1.98 Å)		LYS1164
	ASP1279 (2.15 Å)		TRP1251
	ARG1510 (1.94 Å)		TRP1355
	ASP1526 (1.95 Å)		ASP1420
	HIS1584 (2.20 Å)		MET1421
			SER1425
			LYS1460
			TRP1523
			PHE1559
			PHE1560
			THR1586
Capsaicin	ASP1526 (2.20Å)	PHE1559	ASP1157
			GLN1158
			LYS1164
			TRP1251
			ASP1279
			TRP1355
			TRP1418
			ASP1420
			LYS1460
			ASP1555
			ARG1582
			HIS1584
			THR1586

 

Quantum Chemical Calculations

In order to investigate the main inhibitor-amino acid interactions contributing to the inhibition efficiency of inhibitor on enzyme, quantum chemical calculations were employed. All amino acids in active side of enzyme surrounding the inhibitor within a distance of 4 Å were taken into account. The MP2/6-31G(d,p) level was used for all calculations. The interactions were investigated in term of binding energy (ΔE_binding) expressed as

ΔE_binding = E_{inhibitor–amino acid} – E_inhibitor – E_{amino acid}                                              (6)

where E_{inhibitor-amino acid}, E_inhibitor and E_{amino acid} are the energy of inhibitor-amino acid complex, inhibitor and amino acid, respectively. The inhibitors with molecular surface and amino acid taken into account for the calculations were displayed in Fig. 13-16 for α-amylase and Fig. 17-18 for α-glucosidase. The calculated binding energies were listed in Tables 11-12.

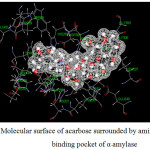Figure 13: Molecular surface of acarbose surrounded by amino acids in binding pocket of α–amylase. Click here to View figure

 

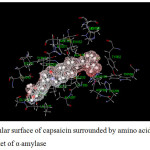Figure 14: Molecular surface of capsaicin surrounded by amino acids in binding pocket of α–amylase. Click here to View figure

 

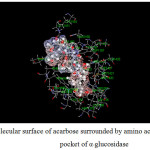Figure 15: Molecular surface of acarbose surrounded by amino acids in binding pocket of α–glucosidase. Click here to View figure

 

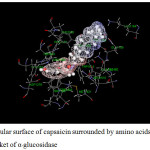Figure 16: Molecular surface of capsaicin surrounded by amino acids in binding pocket of α–glucosidase. Click here to View figure

 

For α-amylase (Table 11), both inhibitors interact with various amino acids. In the case of acarbose, it can interact with amino acids as both attraction and repulsion. The repulsive interactions are caused by ILE235, HIS299, HIS305 and ALA 307 and the interactions vary from 0.2 to 20.3 kcal/mol in which ALA307 provides the largest repulsion. Contrastly, the attractions vary from about -0.8 to -50.2 kcal/mol. The main attractions are caused by the amino acids forming hydrogen bonds with acarbose; ARG195, ASP197, LYS200, GLU233 and ASP300. Although GLY308 forms hydrogen bond with acarbose, the interaction is quite small (-2.3 kcal/mol). Other amino acids yielding attraction interact with acarbose as electrostatic interaction.

In the case of capsaicin, it can interact with α-amylase with less number of amino acids. The attractions vary from about -0.2 to -28.1 kcal/mol. The largest attraction is obtained from LYS200 caused by hydrogen bond. It can be seen that LYS200 and GLU233 provide very high attraction with both acarbose and capsaicin, where as ILE235 yields repulsion with both inhibitors.

Table 11: Binding energy (∆E_binding) between inhibitors and individual residues, calculated at MP2/6-31G(d,p) levels of theory for α-amylase.

Residue	∆Ebinding (kcal/mol)
	Acarbose	Capsaicin
TRP58	-2.11	-0.22
TYR62	-6.41	-1.93
HIS101	-1.37	-0.71
TYR151	-6.89	-3.31
LEU162	-3.77	-1.27
LEU165	-0.83	-0.17
ARG195	-7.26	-1.85
ASP197	-15.82	-4.62
ALA198	-3.21	-1.82
LYS200	-17.01	-28.10
HIS201	-7.31	-2.39
GLU233	-19.35	-12.75
ILE235	0.16	7.04
ASP236	–	-2.99
LEU237	-2.73	-0.71
GLY238	–	-3.31
GLU240	-5.21	-1.27
HIS299	4.94	-0.57
ASP300	-50.15	-5.30
HIS305	2.00	–
GLY306	–	-1.56
ALA307	20.32	-1.53
GLY308	-2.25	–
GLY309	-3.02	–
Summary	-127.27	-61.69

 

For α-glucosidase (Table 12), acarbose yields strong attraction with amino acids, which are LYS1164, ASP1279, ARG1510, ASP1526 and HIS1584 with the binding energy of -11 to -38 kcal/mol. Some electrostatic interactions were also large, e.g. LYS 1460. These interactions mainly contribute to the total energy of -165 kcal/mol. In the case of capsaicin, there is only one hydrogen bond but strong (about -29 kcal/mol for ASP1526). Long hydrocarbon chain of capsaicin can interact with amino acids as electrostatic interaction. The important interactions were provided by ASP1157, ASP1420, LYS1460 and ASP1555. In addition, another interaction of capsaicin and α-glucosidase is π-π interaction which occurs with PHE1559 with the energy of -6.2 kcal/mol. Note that, PRO1159 results the repulsion for both inhibitors with the energy of about 6 and 4 kcal/mol for acarbose and capsaicin, respectively.

The binding free energy and total binding energy obtained from molecular docking and quantum chemical calculation, respectively, of each system were summarized in Table 13. Clearly, the energy obtained from quantum calculation is consistent with that obtained from molecular docking, in which the total binding energy between acarbose and enzymes is larger than capsaicin. In fact, water salvation on protein interactions is very crucial role concerning their enzyme activity, in particular for in vivo test. However, in this case, insights into the molecular docking and/or quantum calculation aspects, water molecule in the active site vicinity is deleted due to aiming of specific atomic coupling interactions between the enzyme substrate and its counter ions of the molecular configuration of the inhibitor studied. H-bond interactions would be actually pronounced, if we concern on their molecular water solvation among the active sites of the enzyme and the inhibitor used. Therefore, it would be affected to the results obtained. However, we have tested this molecular docking and quantum calculation with Acarbose as drug reference. Thus, we can suggest that these data would be lined with physiolocal functions of both enzymes related to antidiabetes activity as well. In addition, since capsaicin contains in chili paper which is a fruit routinely consumed in many countries, one may conclude that it has a potential to be developed as an alternative drug for diabetes.

Table 12: Binding energy (∆E_binding) between inhibitors and individual residues, calculated at MP2/6–31G(d,p) levels of theory for α–glucosidase.

	∆Ebinding (kcal/mol)
Residue	Acarbose	Capsaicin
ASP1157	-38.02	-9.08
GLN1158	-5.19	-2.35
PRO1159	5.99	4.27
LYS1164	-10.05	-3.79
TYR1167	-0.07	-1.11
TYR1251	-4.88	-3.35
ASP1279	-17.98	-0.88
TRP1355	-5.93	-2.95
TRP1418	-4.93	-0.58
ASP1420	-3.95	-6.2
MET1421	-3.11	2.07
LYS1460	-26.15	-5.72
ARG1510	-15.53	1.85
TRP1523	-3.58	-0.59
ASP1526	-16.45	-28.69
ASP1555	–	-23.58
PHE1559	-2.96	-6.24
ARG1582	1.3	-1.11
HIS1584	-11.24	6.24
THR1586	-1.13	-0.34
Summary	-165.03	-82.13

 

Table 13: Total interaction energy between inhibitors and enzymes obtained from molecular docking and quantum chemical calculation.

Enzymes	Inhibitors	Total interaction energy (kcal/mol)
		∆Ebinding(molecular docking)	∆Ebinding(quantum calculation)
α-amylase	Acarbose	-8.16	-128.95
	Capsaicin	-5.78	-62.32
α-glucosidase	Acarbose	-11.93	-172.97
	Capsaicin	-6.08	-78.40

 

Conclusion

This work aims to investigate the inhibitory activity of capsaicin on α-amylase and α-glucosidase enzymes which are carbohydrate hydrolyzing enzymes involving diabetes disease. This is to search for a new diabetes drug. The study employed theoretical approach including molecular docking and quantum chemical calculation. Acarbose, a commercial drug, was also studied for comparison. The first step of this work was re-docking procedure aiming to determine the optimal condition for docking calculation. The re-docking result revealed that the grid box size of 60x60x60 ų was suitable for both enzymes. In addition, 3 rotatable bonds of flexible protein (ASP197, GLU233 and ASP300) and 4 rotatable bonds (ASP1157, ASP1279, ASP1526 and HIS1584) were suitable for α-amylase and α-glucosidase, respectively. These conditions were then used for molecular docking. The docking resulted that, for α-amylase, the binding free energy (ΔG_binding) and inhibition constant (K_i) were about -5.8 kcal/mol and 45.9 µM, respectively. This evaluation was worse compared to acarbose (ΔG_binding = -8.2 kcal/mol and K_i = 0.4 µM). For α-glucosidase, similarly, acarbose yielded better inhibition efficiency with ΔG_binding of -11.9 kcal/mol and K_i of 0.2 nM, whereas capsaicin provided the ΔG_binding of -6.1 kcal/mol and K_i of 23.7 µM. Note that, the inhibitory activity of both inhibitors on α-glucosidase is better than that on α-amylase. For in vitro test, anti-α-amylase activities of Thai varieties of hot chilli extracts were ranged of 43.0-147.0 mg ACE / g DW or 21-51% inhibition [66], while anti-α-glucosidase activities of some chilli pepper extracts were also found to be 23-66%.⁶⁷

The docked structures were later used to investigate the inhibitor-amino acid interactions in which only amino acids surrounding the inhibitor within 4 Å were taken into account. This investigation employed the quantum chemical calculation with MP2/6-31G(d,p) level. The total interaction energy is in agreement with ΔG_binding obtained from molecular docking, and the results revealed that amino acids interacting with inhibitor as hydrogen bond mainly contribute to the total energy. Because acarbose consists of several –OH groups which can form hydrogen bond with amino acids in active site of enzyme, this is a reason that the inhibitory activity of acarbose is higher than capsaicin. Nevertheless, one may say that capsaicin has a potential to be developed as an alternative drug for diabetes disease.

Acknowledgement

This research study was financially supported by Materials Chemistry Research Center, Department of Chemistry and Center of Excellence for Innovation in Chemistry (PERCH-CIC), Faculty of Science, Khon Kaen University, Khon Kaen, Thailand.

References

1. Demir, R.; Cadirci, E.; Akpinar, E.; Cayir, Y.; Atmaca, HT.; Un, H.; Kunak, C.S.; Yayla, M.; Bayraktutan, Z.; Demir, I. Basic & Clinical Pharmacol. Toxicol. 2014, 116(3), 236-243.
   CrossRef
2. International Diabetes Federation: The diabetes epidemic and its impact on Thailand. Bangkok, Novo Nordisk Pharma (Thailand), 2013.
3. Vasanti, S.M. Diabetes Care, 2010, 33(11), 2477-2483.
   CrossRef
4. Ozougwu, J.C.; Obimba, K.C.; Belonwu, C.D.; Unakalamba, C.B. J. Physiol.  Pathophysiol. 2013, 4(4), 46-57.
   CrossRef
5. Libman, I.M.; Becker, D.J. Pediatric Diabetes, 2003, 4(2), 110-113.
   CrossRef
6. Carver, C.; Abrahamson, M. Diabetes Mellitus Overview. Educating Your Patient with Diabetes, 2009, 7(4), 15-27.
   CrossRef
7. Wolson, W. Chem. & Biol., 2007, 14(3), 235-236.
   CrossRef
8. Bhowmik, B.; Akhter, A.; Ali, L.; Ahmed, Y.; Pathan, F.; Mahtab, H. et al. J. Diabetes Investigation, 2015, 6(6), 670-677.
   CrossRef
9. Jo, S.H.; Ka, E.H.; Lee, H.S.; Apostolidis, E.; Jang, H.D.; Kwon, Y.I. Inter. J. Appl. Res. Nat. Prod., 2010, 2(4), 52-60.
10. Kim, S.H.; Jo, S.H.; Kwon, Y.I.; Hwang, J.K. Inter. J. Mol. Sci., 2011, 12(6), 3757-3769.
    CrossRef
11. Asghari, B.; Salehi, P.; Sonboli, A.; Ebrahimi, S.N. Iranian J. Pharma. Res., 2015, 14(2), 609-615.
12. Devi, P.U. J. Nutr. Health & Food Sci., 2014, 2(2), 1-2.
13. Khacheba, I.; Djeridane, A.; Yousfi, M. Inter. J. Carbo. Chem., 2014, 1-12.
14. Nair, S.S.; Kavrekar, V.; Misshra, A. Euro. J. Exp. Biol., 2013, 3(1), 128-132.
15. Thilagam, E.; Parimaladevi, B.; Kumarappan, C.; Mandal, S.C. J. Acupuncture Meridian Studies, 2013, 6(1), 24-30.
    CrossRef
16. Sales, P.M.; Souza, P.M.; Simeoni, L.A.; D. Silveira, J. Pharm. Pharmac. Sci., 2012,15(1), 141-83.
    CrossRef
17. Marques, T.R.; Daetano, A.A.; Simao, A.A.: Castro, F.C.; Ramos, V.O.; Correa, A.D. Revista Brasileira de Farmacognosia, 2015, 26(2), 191-196.
    CrossRef
18. Sudha, P; Zinjardel, S.S.; Bhargava, S.Y.; Kumar, A.R. BMC Compl. Alter. Med., 2011, 11(5), 1-10.
19. Muthubalaji, R.; Ramesh, S.; Kumar, V.V. Der Pharmacia Letter, 2013, 5(4), 241-246.
20. Oboh, G.; Ademosun, A.O.; Ademiluyi, A.O.; Omojokun, O.S.; Nwanna, E.E.; Longe, K.O. Pathol. Res. Inter., 2014, 1(1), 1-7.
    CrossRef
21. Saravanan, S.; Parimelazhagan, T. Food Sci. Human Wellness, 2014, 3(2), 56–64.
    CrossRef
22. Perry, L.; Flannery, K.V. Proc. Nat. Acad. Sci., 2007, 104(29), 11905-11909.
    CrossRef
23. Musfiroh, I.; Mutakin, M.; Angelina, T.; Muchtaridi, M. Inter. J. Pharm. Pharmac. Sci., 2013, 5(1), 248-251.
24. Morris, G.M.; Huey, R.; Lindstrom, W.; Sanner, M.F.; Belew, R.K.; Goodsell, D.S.; Olson, A.J. J. Comput. Chem., 2009, 30(16), 2785-2791.
    CrossRef
25. Morris, G.M.; Goodsell, D.S.; Halliday, R.S.; Huey, R.; Hart, W.E.; Belew, R.K.; Olson, A.J. J. Comput. Chem., 1998, 19(14), 1639-1662.
    CrossRef
26. Silano, V. α-Amylase inhibitors in enzymes and their role in cereal technology. Amer. Assoc. Cereal Chem., St Paul, Minnessota: USA, 1987, l41-199.
27. Ryan, C.A. Ann. Rev. Phytopathol., 1990, 28(1), 425-449.
    CrossRef
28. Peña-Alvarez, A.; Ramírez-Maya, E.; Alvarado-Suárez, L.A. J. Chromatogr. A, 2009, 1216(14), 2843–2847.
29. Ye, X.Y.; Ling, Q.Z.; Chen, S.J. Evidence–Based Compl. & Alter. Med., 2015, 1-6.
30. Darré, L.; Domene, C. Mol. Pharmacol., 2015, 12(12), 4454-4465.
    CrossRef
31. Lambert, J.W.; Sum, A.K. J. Phys. Chem. B, 2006, 110(5), 2351-2357.
    CrossRef
32. Hanson, S.M.; Newstead, S.; Swartz, K.J.; Sansom, M.S. Biophys. J., 2015, 108(6), 1425-1434.
    CrossRef
33. Lee, J.H.; Lee, Y.; Ryu, H.; Kang, D.W.; Lee, J.; Lazar, J. et al.  J. Computer–Aided Mol. Design, 2011, 25(4), 317-327.
34. G. Fernández-Ballester, G.; Ferrer-Montiel, A. J. Membrane Biol., 2008, 223(3), 161-172.
    CrossRef
35. Azeez, S.; Babu, R.O.; Aykkal, R.; Narayanan, R. J. Mol. Modeling, 2012, 18(1), 151-163.
    CrossRef
36. Goldmann, D.; Pakfeifer, P.; Hering, S.; Ecker, G.F. Future Med. Chem., 2015, 7(3), 243-56.
    CrossRef
37. Feng, Z.; Pearce, L.V.; Xu, X.; Yang, X.; Yang, P.; Blumberg, P.M. et al. J. Chem. Inform. & Model., 2015, 55(3), 572-88.
    CrossRef
38. Shukla, A.; Sharma, P.; Prakash, O.; Singh, M.; Kalani, K.; Khan, F. et al. PLoS One, 2014, 9(7), 1-14.
    CrossRef
39. Pandey, A.; Nigam, P.; Soccol, C.R.; Soccol, V.T.; Singh. D.; Mohan, R. Biotech. Appl. Biochem., Pt 2000, 2, 135-152.
    CrossRef
40. Subramanian, R.; Asmawi, M.Z.; Sadikun, A. Acta Biochim. Polon., 2008, 55(2), 391-398.
41. Merritt, A.D.; Rivas, M.L.; Bixler, D.; Newell, R. Am. J. Hum. Genetics, 1973, 25(5), 510–522.
42. Rutten, G.E.H.M.; De Grauw, W.J.C.; Nijpels, G.; Houweling, S.T.; Van de Laar, F.A.; Bilo, H.J. et al.  Huisarts Wet, 2006, 49(1), 137–152.
43. Menichini, F.; Tundis, R.; Bonest, M.; Loizzo, M.R.; Conforti, F.; Statti, G.; Cindio, B.; Houghton, P.J.; Menichint, F. Food Chem., 2009, 114(2), 553-560.
    CrossRef
44. Kim, J.S.; Kwon, C.S.; Son, K.H. Biosci. Biotech. Biochem., 2000, 64(11), 2458-2461.
    CrossRef
45. Ali, H.; Houghton, P.J.; Soumyanath, A. J. Ethnopharmacol., 2006, 107(3), 449-455.
    CrossRef
46. Ortiz-Andrade, R.R.; Garcia-Jimenez, S.; Castillo-Espana, P.; Rameriz-Vila, G.; Villalobos-Molina, R.; Estrada-Soto, S. J.  Ethnopharmacol., 2007, 109(1), 48-53.
    CrossRef
47. Oboh, G.; Akinyemi, J.A.; Ademiluyi, A.O.; Adefegha, S.A. J. Food Nutr. Res. 2010, 49(1), 14-20.
48. Adefegha, S.A.; Oboh, G. Pharmac. Biol., 2012, 50(7), 857-865.
    CrossRef
49. Campbell, J.D.; Trapnell, P.D.; Heine, S.J.; Katz, I.M.; Lavallee, L.F.; Lehman, D.R. J. Personal. Social Psychol., 1996, 70(1), 141-156.
    CrossRef
50. Wachters-Hagedoorn, R.E.; Priebe, M.G.; Heimweg, J.A.; Heiner, A.M.; Elzinga, H.; Stellaard, F.; Vonk, R.J. Diabetic Med., 2007, 24(6), 600–606.
    CrossRef
51. Ceriello, A. Diabetes, 2005, 54(1), 1-7.
    CrossRef
52. Chiasson, J.L.; Josse, R.G.; Gomis, R.; Hanefeld, M.; Karasik, A.; Laakso, M. J. Am. Med. Assoc., 2003, 290(4), 486-494.
    CrossRef
53. Franco, O.L.; Rigden, D.J.; Melo, F.R.; Grossi-de Sá, M.F. Euro. J. Biochem., 2002, 269(2), 397-412.
    CrossRef
54. Kuntz, I.D.; Blaney, J.M.; Oatley, S.J.; Langridge, R.; Ferrin, T.E. J. Mol. Biol., 1982, 161(2), 269-88.
    CrossRef
55. Goodsell, D.S.; Olson, A.J. Proteins, 1990, 8(3), 195-202.
    CrossRef
56. Rarey, M.; Kramer, B.; Lengauer, T. J. Computer–Aided Mol. Design, 1997, 11(4), 369-84.
57. Jones, G.; Wilett, P.; Glein, R.C.; Leach, A.R.; Taylor, R. J. Mol. Biol., 1997, 267(3), 727-748.
    CrossRef
58. Venkatachalam, C.M.; Jiang, X.; Oldfield, T.; Waldman, M. J. Mol. Graph. Model., 2003, 21(4), 289-307.
    CrossRef
59. Friesner, R.A.; Banks, J.L.; Murphy, R.B.; Halgren, T.A.; Klicic, J.J.; Mainz, D.J. et al. J. Med. Chem., 2004, 47(7), 1739-1749.
    CrossRef
60. Schulz-Gasch, T.; Stahl, M. J. Mol. Model., 2003, 9(1), 47-57.
    CrossRef
61. Krovat, E.M.; Steindl, T.; Langer, T. Cur. Comp.-Aided Drug Design, 2005, 1(1), 93-102.
    CrossRef
62. Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Gould, I.R.; Merz, K.M.; Ferguson, Jr.D.M.; Spellmeyer, D.C.; Fox, T.; Caldwell, J.W.; Kollman, P.A. J. Am. Chem. Soc., 1995, 118(9), 2309-2309.
    CrossRef
63. Hehre, W.J. A Guide to Molecular Mechanics and Quantum Chemical Calculations. United States of America: Wavefunction, 2003.
64. Leach, A.R. Molecular modelling: Principles and applications. 2^nd ed. Singapore: Addison Wesley, 1996.
65. Informer Technologies, WebLab ViewerPro. United States of America: Molecular Simulations, 2016.
66. Sricharoen, P.; Lamaiphan, N.; Patthawaro, P.; Nunticha, N.; S. Techawongstien, S.; Chanthai, S. Ultrason. Sonochem., 2017, 38, 629-639.
    CrossRef
67. Watcharachaisoponsiri, T.; Sornchan, P.; Charoenkiatkul, S; Suttisansanee, U. Inter. Food Res. J., 2016, 23(4), 1439-1445.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.