Conductimetric Properties of Benzoic Acid in Water and 1-Propanol Mixtures at the Temperatures from 298.15 to 313.15K

Introduction

The binary solvent systems are important for many practical applications, such as, in HPLC analysis,¹ in MALDI-TOF analysis,²in the study of several physicochemical properties of electrolyte solutions.³It has attracted the researchers to study the effect of physical properties of solvents on dissociation of acids and electrolytes. Literarure reveals that few studies on the dissociation constants of benzoic acid and derivative of benzoic acids in alkanol-water mixtures by conductometric methods have been performed earlier.^4-8But no report about the investigation on the conductometric studies of benzoic acid in 1-propanol mixture are available yet.

Conductometric studies can be used to determine the purity of solvent, relative ionic strength, dissociation constant of acids, solubility product etc. ⁹The present paper reports molar conductance of dilute solution of benzoic acid in 1-propanol-water binary mixtures ranging in composition from 0 to 40 wt% 1-propanolin waterat 5K interval from 298.15 to 313.15K. Thermodynamic dissociation constant pK_a was estimated from the measured conductance data using Bray-Kraus¹⁰ and Fuoss-Kraus¹¹ equations. From the relation between the pK_a and the composition of the solvent mixtures, solute-solvent interaction can be assessed. The free energy of transfer ∆G^o_tr of carboxylate ions from water to alcohol-water mixtures is also discussed.

Materials and Method

Chemicals

Benzoic acid (BDH), 99.9% pure was used without further purification. 1-Propanol (Fisher chemicals, Fisher Scientific UK. Ltd.) was used for the preparation of mixed solvents without further distillation. The specific conductance of 1-propanol was measured to be 0.3-0.4×10^-6ohm^-1cm^-1at room temperature. Doubly distilled water was used for preparing the mixed solvents. The specific conductance of water was measured to be 1.2-1.5 ×10^-6   ohm^-1   cm^-1 at room temperature.

Preparation of Mixed Solvents and Benzoic Acid Solutions

1-propanol-water mixed solvents were prepared in weight-by-weight ratio, using measured volumes of the liquids multiplied by their respective densities at the temperature of mixing (room temperature). Density values of the liquids were used from the standard charts.

A stock solution of the acid was prepared by dissolving weighed amount of the solute in a definite volume of the solvent, secondary stock solutions were prepared from this solution by dilution. During conductance measurement, different aliquot of the stock acid solutions were added to a suitable volume of the solvent taken in a glass cell to prepared solutions of different concentrations.

Apparatus

Thermostatic water bath having a temperature accuracy of + 0.05⁰C was used for equilibrating all solutions before conductance measurement. A simple glass cell of approximately 50 ml capacity with an adjustable plastic covering was used for taking the solutions for conductance measurement. Conductometer, model DDS-307 with dip type cell was used for conductance measurement. The accuracy of the cell was ± 1%.The Specific conductance of a solution was directly read out from the meter.

Procedure

A suitable volume of the solvent was pipetted into pyrex glass cell, placed in the thermostatic bath and properly clamped. A small aliquote of the stock acid solution pipetted into the glass cell with help of a 1 mL pipette. The mixture was mixed properly with the cell electrode and equilibrated to the bath temperature. Specific conductance of the solution was read directly from the conductivity meter. In this way, solutions of gradually decreasing concentrations were prepared by adding more of the 1-propanol-water solvent mixtures and their specific conductance was measured.

Result and Discussion

The dissociation constant (K_a) of benzoic acid was investigated at seven different percent of 1-propanol in the water-propanol mixtures in the range of 0-40% of 1-propanol from 298.15 to 313.15 K at 5 K interval. The molar conductances (Λ) of benzoic acid at different concentrations (C) of benzoic acid are given in Table1.

The experimental molar conductances of benzoic acid were first analyzed by Bray-Kraus¹⁰ Equation1 to obtain the limiting molar conductance (Λ).

Λ_° valuesfor each percent 1-propanol solution at each temperature calculated from the intercept of the plots of (1/Λ) vs.(Λ x C) values from the Bray-Kraus equation were then used to calculate Ka values of benzoic acid from the least square fitting of the Fuoss-Kraus¹¹ Equation 2.

Where, Fuoss function F_(z) and activity coefficient f_±  calculated as the stated by Fuoss-Kraus model.¹¹ Thus, from the plot of

versus

the slope

can be obtained. From the values of slope K_a was calculated.

Table 1: Molar conductance() of benzoic acids in 1-propanol-water mixtures at different temperatures.

Concentration(Mole L-1) x104	Molar conductance ()/ ohm-1cm-1
	T/K	T/K	T/K	T/K
	298.15	303.15	308.15	313.15
0 wt% of 1-propanol
3.830	112.80	110.97	108.88	114.63
3.556	115.85	114.44	112.20	118.10
3.319	119.00	117.50	115.39	121.41
3.112	122.12	120.83	118.58	124.37
2.929	125.31	123.60	121.21	127.36
2.766	127.98	126.54	124.01	130.15
2.620	130.90	128.99	126.70	132.80
2.489	132.96	131.36	129.35	135.37
5 wt% of 1-propanol
5.234	85.40	81.27	80.00	78.92
4.972	87.49	83.11	81.97	80.82
4.735	89.12	84.87	83.87	82.66
4.520	90.93	86.58	85.53	84.47
4.144	94.12	88.27	87.39	86.06
3.825	97.26	91.47	90.74	89.30
3.552	100.24	94.91	93.60	92.55
3.315	103.17	97.70	96.29	95.17
10 wt% of 1-propanol
6.577	58.38	58.23	57.02	55.80
6.166	60.17	59.84	58.71	57.41
5.803	61.69	61.52	60.31	59.10
5.481	63.13	62.94	61.85	60.57
5.193	64.71	64.52	63.36	62.01
4.933	66.09	65.88	64.67	63.25
4.485	68.90	68.68	67.57	66.01
4.111	71.28	71.28	69.82	68.60
15 wt% of 1-propanol
7.129	42.643	41.381	41.661	42.082
6.654	44.036	42.684	42.984	43.435
6.238	45.369	43.926	44.246	44.727
5.871	46.672	45.139	45.650	45.990
5.545	47.793	46.531	46.711	47.072
5.253	48.923	47.594	47.974	48.355
4.990	50.098	48.695	48.896	49.497
4.537	52.243	50.700	51.141	51.582
20 wt% of 1-propanol
6.499	30.238	30.007	29.391	30.469
6.092	31.104	30.202	31.351	30.940
5.734	32.002	31.217	32.351	31.828
5.415	32.869	32.038	33.146	32.685
4.874	34.469	33.649	34.777	34.264
4.431	35.998	35.095	36.337	35.772
4.062	37.547	36.562	37.793	37.301
3.749	38.808	37.601	37.875	39.075
30 wt% of 1-propanol
8.367	14.103	14.283	14.462	14.641
7.902	14.490	14.844	15.034	14.667
7.486	14.868	15.228	15.055	15.415
7.112	15.228	15.425	15.608	15.791
6.773	15.591	15.960	16.152	15.783
6.465	15.926	16.117	16.318	16.504
6.184	16.251	16.445	16.639	16.849
40 wt% of 1-propanol
8.687	8.611	8.806	8.944	9.082
8.325	8.781	9.129	9.273	8.985
7.992	8.946	9.309	9.459	9.159
7.685	9.122	9.486	9.642	9.330
7.400	9.297	9.662	9.811	9.500
7.136	9.459	9.824	9.978	9.683
6.890	9.623	9.841	10.000	10.027

 

The limiting molar conductance (Λ_o) value of benzoic acid in aqueous medium was found to be 362.98 S cm^-1mol^-1.Niazi et al¹² reported the Λ_o for benzoic acid to be 383.55 ± 1.16 S cm^-1mol^-1. Strong et al¹³ have also reported Λ_o for benzoic acid to be 383.14 ±1.76 . Table 2 shows that with the increase of the proportion of 1-propanol in the 1-propanol-water mixtures the Λ_o values of benzoic acid decrease. This type of observed result may be due to the relative increase in the viscosities of 1-propanol-water mixtures. The decrease of Λ_o values may be the resultant of their overall effect facilitating the thermal movement of the ions.

Table 2: Λ_o Values for Acids in Alcohol-Water Mixtures at Different Temperatures.

T/K	Λo / ohm-1cm-1
	0 wt%	5 wt%	10 wt%	15 wt%	20 wt%	30 wt%	40 wt%
298.15	362.98	315.50	270.53	263.47	229.29	143.41	151.75
303.15	364.70	324.63	272.72	275.12	238.78	138.16	144.17
308.15	368.60	335.23	280.31	286.89	260.42	134.31	142.54
313.15	369.55	347.55	286.40	284.22	219.68	128.87	136.14

 

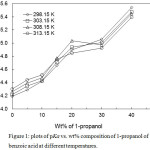Figure 1: plots of pKa vs. wt% composition of 1-propanol of benzoic acid at different temperatures. Click here to View figure

 

The pKa values calculated from the thermodynamic dissociation constant are presented in Table 3. The value tthermodynamic dissociation constant (pK_a) of benzoic acid in aqueous solution was found 4.26 that were in complete agreement with the reported values.^12,15The relation between the pK_a values of the acid and the percent of 1-propanol in 1-propanol-water mixtures is shown in Figure 1.The pK_a values increased with the increase in concentration of 1-propanolin the binary mixtures of 1-propanol-water. The increase in pK_a values with the increase of the alcohol concentration (as dielectric constant decreases) may be due to dominating influence of coulombic forces of attraction over the dispersive force of attraction. Gloverset al.¹⁶ and Fong et al.¹⁷ determined the dissociation constant K_a of propionic acid in ethanol-water mixtures potentiometrically and observed a similar trend in the pK_a vs. wt%. They also noticed a similar trend in the temperature variation of the pK_a values similar to present investigation.

Table 3: pK_aValues of Benzoic Acids in 1-propanol-Water Mixtures at Different Temperatures.

T/K	pKaValues
	0 wt%	5 wt%	10 wt%	15 wt%	20 wt%	30 wt%	40 wt%
298.15	4.260	4.287	4.417	4.660	4.895	5.057	5.539
303.15	4.285	4.345	4.428	4.715	4.938	5.011	5.473
308.15	4.312	4.390	4.474	4.770	5.038	4.974	5.448
313.15	4.327	4.440	4.516	4.754	4.846	4.924	5.393

 

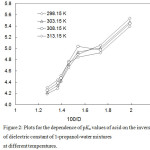Figure 2: Plots for the dependence of pKa values of acid on the inverse of dielectric constant of 1-propanol-water mixtures at different temperatures. Click here to View figure

 

The relation between the pK_a values of benzoic acid and the inverse of dielectric constants of solvent mixtures is shown in Figure 2. From the figure it is shown that the plots are non linear. This nonlinearity indicates that there are some specific solute-solvent interaction among the ions and the solvent mixtures. This is further evident from the values of ∆G^o_tr   for carboxylate ions on their transfer from water to co-solvent-water mixtures. The free energy of transfer of benzoic acid from water to 1-propanol-water mixtures are calculated from the equation, ∆G^o_tr = RT 2.303 (pK_a^s– pK_a^w) where  s and w referred to solvent mixtures and water respectively.The plots of the thermodynamic parameters for the transfer of benzoic acid from water to water-1-propanol mixtures are shown in Figure 3. These plots are also nonlinear. The values of the thermodynamic transfer energies are consistent if we examine the ∆G^o_tr with the dielectric constant of the media. With a lowering of the dielectric constant of the media by the addition of the 1-propanol in the 1-propanol-water mixtures, the force of attraction between the oppositely charged ions increases, thereby pK_a increases, requiring higher energy to transfer the species from the aqueous to non-aqueous media. The plots of ∆G^o_trvs. solvent mixtures have been found the same as reported by Niazi et al.¹²

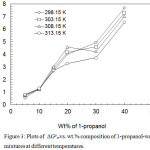Figure 3: Plots of  ∆Gotrvs. wt.% composition of 1-propanol-water mixtures at different temperatures. Click here to View figure

 

The normalized Walden products (nwp) are calculated in our case at different wt% and at different temperatures. They are graphically presented in the Figure 4. A good agreement of the nwp was also observed by Niazi et al¹² in case of benzoic acid and other acids in propanol- water and number of other aqueous–alcohol mixtures at 25^oC. They concluded that this trend of the nwp values might not be due to the change of viscosities or dielectric constant, but also to an altering proton transfer mechanism as solvent is enriched with organic component. In our case there is no systemic trend in the nwp with the increase in 1-propanol concentration of the solvent mixtures. But nwp values of benzoic acid generally decrease with the increase in temperatures. Conway et al¹⁴observed that the nwp values passed through a maximum at about 15 to 25 wt% alcohol concentration in the solvent mixtures which is in good agreement with our results.

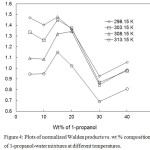Figure 4: Plots of normalized Walden products vs. wt % composition of 1-propanol-water mixtures at different temperatures. Click here to View figure

 

Acknowledgments

The Authors expresses honest appreciation to the Department of Chemistry, CU, Bangladesh for providing lab facilities for this research.

Conclusion

The solubility of benzoic acid in water increases with an increment of the propanol in water concentration which corresponds that the co-solvent of propanol enhanced the solubility of the benzoic acid. There is no regular trend of thermodynamics dissociation constant of benzoic acid in the range of temperature between 298.15 to 313.15K. Benzoic acid dissociation in propanol co-solvent is spontaneous above the temperature 298.15K.

References

1. Hara, S., Fujii, Y., Hirasawa, M., Miyamoto, S. J. Chromatogr. A.1978, 149, 143-149.
   CrossRef
2. Chen, H., Guo, B. Anal. Chem., 1997, 69, 4399–4404.
   CrossRef
3. Kay, R.L., Broadwater, T.L., Electrochim. Acta. 1971, 16, 667-676.
   CrossRef
4. Roses, M., Bonet, M.J., Bosch, E. Anal. Chim. Acta.1996, 333, 241-247.
   CrossRef
5. Wang, H., Wang, Q., Xiong, Z., Chen, C., Shen, B. J. Chem. Thermodyn.2015, 83, 61-66.
   CrossRef
6. Yurquina, A., Manzur, M. E., Brito, P., Manzo, R., Molina, M. A. A. J. Mol. Liq.2003, 108, 119-133.
   CrossRef
7. Kumari, A., Sandeepa, K., Prathap, K. T., Satyavathi, B.  J. Chem. Eng. Data. 2016, 61, 67-77.
   CrossRef
8. Long, B., Li, J., Zhang, R., Wan, L. Fluid Phase Equilib.2010, 297, 113-120.
   CrossRef
9. Glasstone, S. EWP, 1942.
10. Kraus, C.A. and Bray, W.C.J. Amer. Chem. Soc.1913, 35, 1315.
    CrossRef
11. Fuoss, R. M. and Kraus, C.A. J. Chem. Soc. 1933, 55, 476.
    CrossRef
12. Niazi, M. S. K., Shah, S. S., Ali. J.and Khan. M. Z. I., J. Sol. Chem. 1990, 19, 623.
    CrossRef
13. Strong, L. E., Blubaug, D., J. Kallmeyer J. B. and Taylor S. P. J. Phys. Chem.1985, 89, 1318.
14. Conway, B.E., Bokris, J. O. M. and Linton, H. J. Phys. Chem.1956, 24, 834.
    CrossRef
15. DASH, U. N. J. Indian Chem.Soc.1994, 71, 65-69.
16. Glovers, D. J. J. Amer. Chem. Soc.1965, 87, 5275.
    CrossRef
17. Fong, D. and Grunwald, E. J. Chem. Soc. 1969, 73, 3909.

---

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.