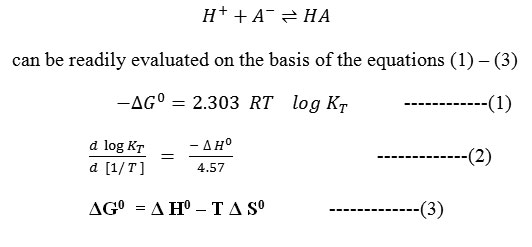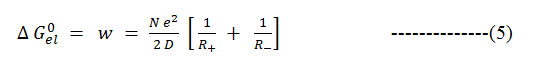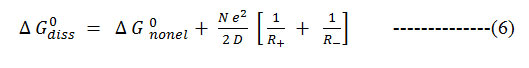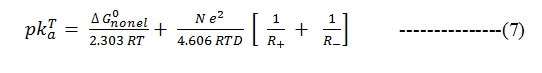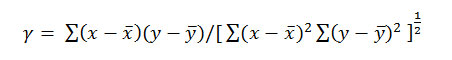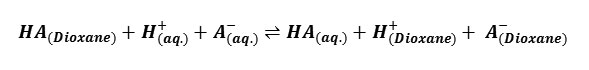Thermodynamic Proton – Ligand Satability Constants in Dioxane – Water Media, Pk_a , Δg⁰, Δ H⁰ And  Δ S⁰, Values for 1, 3 – Disubstituted Barbituric Acid

INTRODUCTION

Barbituric acid are have found immense analytical and medicinal applications^1-6. However, such applications necessitate a precise knowledge of their protonation constants. Recently, several analogous compounds have been synthesised by the introduction of substituent groups in different positions for improved analytical characteristics. This empirical approach, although sometimes inescapable , is generally wasteful and it is more fruitful to determine the physicochemical properties of the reagents and their resulting metal complexes, and in particular their protonation constants, which could lead to a better understanding of the cause of specificity and selectivity of relevant medicinal and analytical reactions. With this value, the thermodynamic protonation constant [ ] of 1, 3 di substituted barbituric acids in different mole fraction of dioxane at 20, 30, and 40  0.10⁰C have been determined. The thermodynamic functions, associated with protonation processes have also been evaluated.

EXPERIMENTAL

The substituted barbituric acids were synthesised by the usual procedure reported in the literature⁷ and recrystallized before use and the purity was checked by analytical analysis, UV and IR spectra. All other chemicals were of Anala R and G.R grades of B.D.H or E. Merck unless otherwise stated. Dioxane was purified using the method of Weissberger et al⁸ or carbonate free sodium hydroxide was prepared by the electrolytic method of Vogel⁹.

The protonation constant were determined by the pH-titration method employing a pH-meter cell of type.

Ag, AgCl  HCl, glass, KCl, Acids, HClO₄– NaClO₄  NaOH   KCl,   Hg₂Cl₂

[To maintain I = 0.1 M]

The pH values measured with an expanded scale pH- meter were corrected from the calibration curves to obtain the true pH values. From the potentiometric titrations of HClO₄ in the absence and presence of barbituric acids, the formation curves in which  [the average number of protons bound per free ligand] plotted against pH were constructed in accordance with the procedure of Irving and Rossotti¹⁰. By applying Bjerrum’s¹¹ 10 half integral method, the protonation constants at three temperatures were determined, the correction for activity coefficient were applied on the basis of Davies equation¹² and the thermodynamic protonation constants were evaluated. The change in free energy ΔG⁰, enthalpy Δ H⁰ and entropy Δ S⁰ associated with the protonation equilibrium, i.e

Formula 1 to3

 

RESULT AND DISCUSSION

The thermodynamic protonation constant [_PK^T_a ] at temperatures -20, 30 and 40⁰C are given in table-1. The average [_PK^T_a ] generally falls within

Table – 1 _PK^T_a values of 1, 3 – di substituted Barbituric acids at different Temperatures

Acids	Mole fraction of dioxane (
	0a			0.175			0.250			0.350
	200C	300C	400C	200C	300C	400C	200C	300C	400C	200C	300C	400C
DMBA	3.85	3.74	3.65	4.18	4.00	3.92	4.25	4.12	4.02	4.33	4.21	4.10
DPBA	4.07	3.98	3.92	4.35	4.22	4.09	4.44	4.35	4.24	4.60	4.48	4.39
D-p-TBA	4.29	4.18	4.08	4.54	4.45	4.35	4.70	4.58	4.46	4.85	4.74	4.63
D-m-TBA	3.98	3.88	3.79	4.23	4.14	4.03	4.34	4.23	4.10	4.48	4.36	4.24
D-o-TBA	3.57	3.48	3.40	3.82	3.69	3.58	3.86	3.77	3.66	3.96	3.88	3.78
D-o-XBA	3.66	3.57	3.46	3.85	3.76	3.64	3.96	3.84	3.71	4.04	3.95	3.85
D-m-XBA	4.38	4.28	4.19	4.68	4.57	4.45	4.79	4.68	4.56	4.97	4.85	4.74
D-p-XBA	3.94	3.83	3.72	4.16	4.05	3.92	4.27	4.15	4.03	4.39	4.27	4.15
D-p-ABA	4.12	4.00	3.89	4.46	4.35	4.25	4.57	4.45	4.32	4.70	4.58	4.45
D-α-NBA	4.33	4.22	4.13	4.58	4.48	4.37	4.74	4.62	4.52	4.80	4.68	4.57

o^a →Extrapolated values at 0 % dioxane.

a spread of ±0.02 but not beyond ±0.03 in any case. The empirical data for the mole fraction of dioxane (n₂) and ΔG⁰, Δ H⁰ and Δ S⁰ values are given in the table 2 and 3 respectively. The _PK^T_a values increase in dioxane content because of the decrease in the dielectric constant of bulk solvent. As the dielectric constant decreases, the ion interaction involving the proton and anionic oxygen on the ligand decrease to a greater extent than the ion dipole interaction between the proton and the solvent molecule. A plot of _PK^T_a  against mole fraction of dioxane [ Fig.1] shows a linear relationship of the form.  _PK^T_a = mn₂ + c.

Table – 2 Empirical correlation _PK^T_a  of  with mole fraction of dioxane (n₂)

Acids	Temp. (0C)	PKTa  = m  + c
		Last square method			graphically
		m	c	r	m	c
DPBA	20	5.66	3.96	1.00	5.63	3.98
	30	5.64	3.88	0.99	5.61	3.90
	40	5.63	3.80	1.00	5.62	3.82
DMBA	20	5.56	3.81	1.00	5.54	3.82
	30	5.53	3.72	1.00	5.52	3.74
	40	5.52	3.64	1.00	5.50	3.65
D-p-TBA	20	5.69	4.20	1.00	5.68	4.18
	30	5.68	4.11	1.00	5.67	4.10
	40	5.66	4.05	1.00	5.65	402
D-m-TBA	20	5.09	3.65	1.00	5.08	3.68
	30	5.09	3.60	0.99	5.08	3.63
	40	5.08	3.52	1.00	5.05	3.57
D-o-TBA	20	5.03	3.44	0.99	5.02	3.45
	30	5.03	3.39	1.00	5.02	3.40
	40	5.02	3.33	1.00	5.00	3.34
D-o-XBA	20	5.78	3.60	1.00	5.76	3.59
	30	5.75	3.53	1.00	5.74	3.52
	40	5.73	3.48	0.99	5.72	3.46
D-m-XBA	20	5.14	4.00	0.99	5.12	4.02
	30	5.14	3.94	1.00	5.12	3.96
	40	5.12	3.88	1.00	5.10	3.90
D-p-XBA	20	5.25	3.65	1.00	5.23	3.62
	30	5.25	3.55	1.00	5.23	3.54
	40	5.24	3.50	0.99	5.22	3.48
D-α-NBA	20	5.36	3.57	1.00	5.35	3.56
	30	5.37	3.52	1.00	5.35	3.50
	40	5.36	3.46	0.99	5.34	3.44
D-p-ABA	20	5.44	3.50	0.99	5.42	3.48
	30	5.43	3.43	1.00	5.42	3.42
	40	5.43	3.37	1.00	5.40	3.35

 

Gurney¹³ and others ^{14, 15} have shown that the standard free energy change associated with the proton transfer, ΔG⁰_diss, may be split into two distinct parts: electrostatic [el.] and none electrostatics [nonel].

Formula 4

 

The electrostatic contribution to the free energy change is often estimated using Born equation¹⁶.

Formula 5

 

Where R₊ and R _–  are radii of solvated ions and D is the dielectric constant of the medium^{17, 18}. Hence

Formula 6

 

Further, as ΔG_diss = 2.303 RT  _PK^T_a¹⁵ , the equation simplifies as

Formula 7

 

against 1/D assuming ΔG⁰_nonel. to be independent of the solvent. When the _PK^T_a  values of substituted barbituric acids are plotted against 1/D it is observed that the plots possess a distinct curvature. It seems evident that non-electrostatic factors exert a considerable influence on the deprotonation of barbituric acids.

For barbituric acids, the change in  _PK^T_a  with mole fraction of dioxane (η₂) is of considerable magnitude. Generally, the difference in  _PK^T_a   in aqueous medium ( η₂= 0) and aqueous dioxane medium ( η₂= 0.350) is of the order of 1.45 – 1.95 _PK^T_a   units. When _PK^T_a values of these barbituric acids are plotted against n₂, the straight line relationship are encountered [Fig 1]. The experimental values of _PK^T_a  here indicate a maximum deviation from linearly of the order of 0.05 or about 0.5% in _PK^T_a .

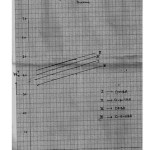Figure 1 Click here to View Figure

 

The goodness of fit in these instances was judged by calculating the correlation coefficient, , defined by­­&nbsp

Formula 8

 

Where  and   are mean values of x (_PK^T_a)  and y (η₂), respectively. The summations are extended to all pairs (x, y) a variable. Linear proportionality is readily indicated between the variables when the value of  is γ +1.0.

Since the value of γ   is approximately +1.0 at 20, 30 and 40⁰C for all the substituted barbituric acids. [ Table-2], it implies that there is quite a high probability of a linear relationship between (_PK^T_a) and η₂. A similar behaviour is found for several other acids such as benzoic, acetic propionic and formic acids¹⁹. 18 in aqueous dioxane medium. Likewise, linear proportionality is also obtained for some other mixed water solvents, e.g: acetic, propionic, butyric and benzoic acids in methanol-water mixtures²⁰.

The _PK^T_a values have been determined with a precision of ±0.02 to ±0.03 and hence the error in ΔG⁰ is believed to be close to ±0.03 and ±0.04 Kcal/mole. The values of Δ S⁰ given in table -3 are accurate to ±0.02 cal.mole ^{– 1} K ^{– 1} .

Table – 3  ΔG⁰ Δ H⁰ and Δ S⁰ values for 1,3 – di substituted barbituric acids at 30⁰C

Table 3: ΔG0 Δ H0 and Δ S0 values for 1,3 – di substituted barbituric acids at 300C Click here to View table

The negative value of Δ H⁰ found in aqueous as well as dioxane mixtures for all barbituric acids proves that their protonation at temperatures up to 40⁰c is exothermic. The negative values of Δ H⁰   encountered here may be described to the formation of the covalent bond between proton and anionic oxygen on the barbituric acids. Further, It is evident that the magnitude of Change in, Δ H⁰ with solvent composition is relatively small and falls with in the range of experimental error. it is because of this that the slopes of straight lines in the plots of _PK^T_a against n₂ (Fig – 1 ) do not differ markedly and are nearly the same and parallel at the three temperatures for all the barbituric acids.

The values of Δ S⁰ are found to increase with increase in dioxane content of the solvent medium for all barbituric acids, there by proving that it is dependent of solvent composition. The net entropy changes associated with protonation process can be attributed to a combination of the following

(i). Change neutralisation; (ii) Subsequent liberation of ordered water molecules; and (iii) loss of rotational and vibrational degrees of freedom of the legend only (iii) gives a small negative contribution to entropy, but the contributions of (i) and (ii) together more than offset that due to (iii) and hence the protonation process has large positive Δ S⁰ values. The protonation of these acids then appears to be entropy driven as expected from the degree of change neutralisation and polarizability of the resulting anions.

When the acid protonates in two media, the free energy change for the transfer reaction from one medium to the other is given by 2.303 RT _PK^T_a . For instance with DPBA, Δ G⁰_(aq.) and Δ G⁰_{(  = 0.175)} are 5.50 and 5.83 Kcal mole ^{– 1}, respectively at 30⁰ and Δ G⁰ changes by 0.33 Kcal mole ^{– 1} in the transfer reaction.

Formula 9

 

and this result in a change of 0.20 Cal mole ^{– 1} in entropy. _PK^T_a Δ  (S – W) values, ie _PK^T_a ;  (S) –  _PK^T_a  (W) (where S and W refer to mixed solvents and water respectively) of barbituric acids are given in table 4. The change in _PK^T_a  (S – W) which is found to be different for the different acids for the same percentage of dioxane is probably due to the presence of different substituents which cause a great change in the distribution of electron density in the ring and hence the electron density at any particular point is also affected.

Table – 4 _PK^T_a Δ  (S – W) = (S) –  _PK^T_a  (W)

Acids	Mole fraction of dioxane (
	0.1750C			0.250			0.350
	200C	300C	400C	200C	300C	400C	200C	300C	400C
DMBA	0.33	0.26	0.27	0.40	0.38	0.37	0.48	0.47	0.45
DPBA	0.28	0.24	0.17	0.37	0.37	0.32	0.53	0.50	0.47
D-p-TBA	0.25	0.27	0.27	0.41	0.40	0.38	0.56	0.56	0.55
D-m-TBA	0.25	0.26	0.24	0.36	0.35	0.31	0.50	0.48	0.45
D-o-TBA	0.26	0.21	0.18	0.29	0.29	0.26	0.39	0.40	0.38
D-o-XBA	0.19	0.20	0.19	0.30	0.27	0.25	0.38	0.38	0.39
D-m-XBA	0.30	0.29	0.26	0.41	0.40	0.37	0.59	0.57	0.55
D-p-XBA	0.22	0.23	0.20	0.33	0.32	0.31	0.45	0.44	0.43
D-p-ABA	0.35	0.34	0.36	0.45	0.44	0.43	0.58	0.58	0.56
D-α-NBA	0.25	0.26	0.24	0.41	0.40	0.39	0.47	0.46	0.54

 

ACKNOWLEDGEMENTS

Thanks are due to the department of chemistry, Sahu Jain (PG) college, Najibabad for providing the necessary facilities and also to the  I.I.T. Roorkee for providing library facilities.

REFERENCES

1. N. Haque, J. N. Roedel, I. P. Lorenz, Z. Anorg. Allg. Chem. 2009, 635,496 – 502.
2. N. Haque, B. Neumann, I. P. Lorenz, Z. Naturforsch. 2010, 65 b, 101 – 106.
3. N. Haque, B. Neumann, P. Mayer, I. P. Lorenz, J. Organomet. Chem. 2010 manuscript in preparation.
4. M. Meusel, A. Ambrozak, T. K. Heckes, M. Gutschow, J. Org.Chem. 68, 4684 (2003).
5.  H. Brunner, K. P. Ittner, D. Lunz, S. Schmatlock, T. Schmidt, M. Zabel, Eur. J. Org. Chem. 855, (2003).
6. E. Chansah, D. S. Weiss, Neuropharmacology 40, 327, (2001).
7. M. Ridi, P. Viturini and L. Zipatti, Ann. chiqn. , 42, 25(1952).
8. A Waissberger, E. S. Proskauer, J. A. Riddick and E. E. Troopes. Jr, Techniques of organic Chemistry, vol. VII, Interscience, New York, P. 126.
9. A. I. Vogel, A textbook of quantitative Inorganic Analysis, Longmans, 3^rd edn., 1961. P;239.
10. H. M. Irving and H. S. Rossotti, J. Chem. soc., 2904(1954).
11. J. Bjerrum, Metal-Amine formation in aqueous solution, P. Hasse and sons, Copenhagen, 1941.
12. C. W. Davies, Ion association, Butter Worths, London, 1962, chap;3.
13. R. W. Gurney, J. Chem phys. 6, 499(1938).
14. H. L. Kapoor and Y. K. Agrawal, J. Chem. Eng. Data, 22, 159, (1977).
15. S. G. Tandon and Y. K .Agarwal, Talanta. 19, 700, (1972).
16. M. G. Born, Z. Phys., 1, 45, (1920).
17. M. Mandel, Bull. Soc.. Chem. Belg, 64,44,(1955).
18. M. Mandel and A. Jenard, Bull. Soc. Chem. Belg., 64, 575(1958).
19. H. S. Harned and B. B. Owen, The Physical Chemistry of Electrolytic Solutions, Reinbold, New York, 3^rd edn., 756(1958).
20. R. H. Stoks and R.S. Robinson, Electrolytic Solutions, Buller-works, London 541(1955).

---

This work is licensed under a Creative Commons Attribution 4.0 International License.